一种热成型钢热压缩流变行为的本构方程
2014-03-08冯泽林陈其伟王会廷
冯泽林,陈其伟,王会廷
(安徽工业大学材料科学与工程学院,安徽马鞍山243002)
热成型钢具有高的室温强度和良好的综合性能,被广泛应用于汽车工业中。高强度钢的热冲压成型加工工艺是将钢板加热至奥氏体状态,保温一段时间后进行冲压并淬火处理的过程。淬火目的是保证钢板在室温下获得均匀马氏体组织[1],从而提高钢板的强度,抗拉强度可达1 000 MPa以上[2-3]。在金属材料的成型过程中,流变应力对产品的加工工艺和质量有重要的影响,而流变应力的大小与变形温度、应变速率及应变量有关,也与材料成分、晶粒尺寸和变形历史等因素有关[4]。林建平等[5]利用Zener-Hollomon参数的正弦形式表述USIBOR1500钢的高温拉伸变形时的流变应力,采用井上胜郎模型来研究该钢种的流变行为,较好地描述了峰值应变前的应力-应变关系;李辉平等[6]采用以Arrhenius为基础构建的铜、镁、铝、钛等合金材料的热塑性变形本构模型,计算高温状态下等温拉伸实验的流变应力,并与实验值进行对比,验证预测结果的可靠性。文中采用井上胜郎模型,研究新开发的1种热成型钢在高温压缩过程中的流变应力与温度、应变、应变速率的本构关系,为该钢种后续的热成型模拟研究提供准确的理论模型。
1 实 验
1.1 实验材料
实验材料为热成型钢,化学成分如表1,将其机加工成10 mm×15 mm的试样。

表1 热成型钢的化学成分(w/%)Tab.1 Chemical compositions of hot stamping steel(w/%)
1.2 实验方案
采用Gleeble-3500型热模拟试验机进行高温热压缩实验。选取变形温度为773,873,973,1 073,1 173 K;应变速率为0.01,0.10,0.50 s-1;试样的压缩变形量为60%。为减小摩擦对应力状态的影响,在试样两端涂覆润滑剂并加石墨垫片。试样升温速率为15 K·s-1,加热至预定温度保温5 min,进行高温热压缩实验,得出其变形过程中的应力-应变曲线;通过拟合回归分析该热成型钢高温变形过程中的本构模型,并对其应变行为进行探讨。
2 实验结果与讨论
2.1 应力-应变曲线
图1为经热压缩实验测得的热成型钢在不同条件下的应力-应变曲线,由图1可见:不同温度条件下,热成型钢的应力随着应变增加而增大,此阶段加工硬化起主导作用;在同一温度、不同应变速率条件下,对于同一应变值,应变速率越大,对应的应力越大;在低应变速率下(图1(d),(e)),应力随着应变的增加迅速上升,当达到一定的应变后,应力基本不变,即出现稳态流变特性,此阶段发生了动态回复和动态再结晶,从而产生软化;变形温度为773 K时,热成型钢在小应变速率条件下变形,可能发生了部分贝氏体转变,使得该温度时0.01 s-1与0.1 0 s-1的应力-应变曲线几乎相同;变形温度为873 K时,热成型钢的流变应力最大达到300 MPa左右,而当变形温度达到1 073 K时,流变应力最大值降至150 MPa左右,可见,对于热成型钢,可通过提高钢坯的变形温度以降低材料的流变应力。
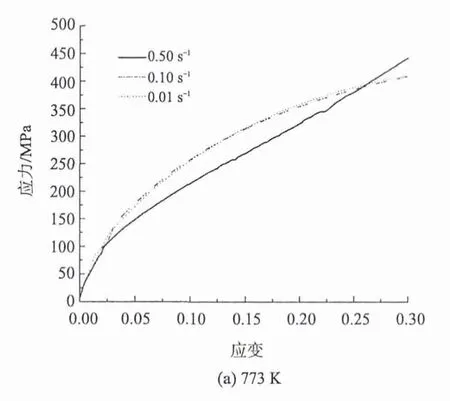
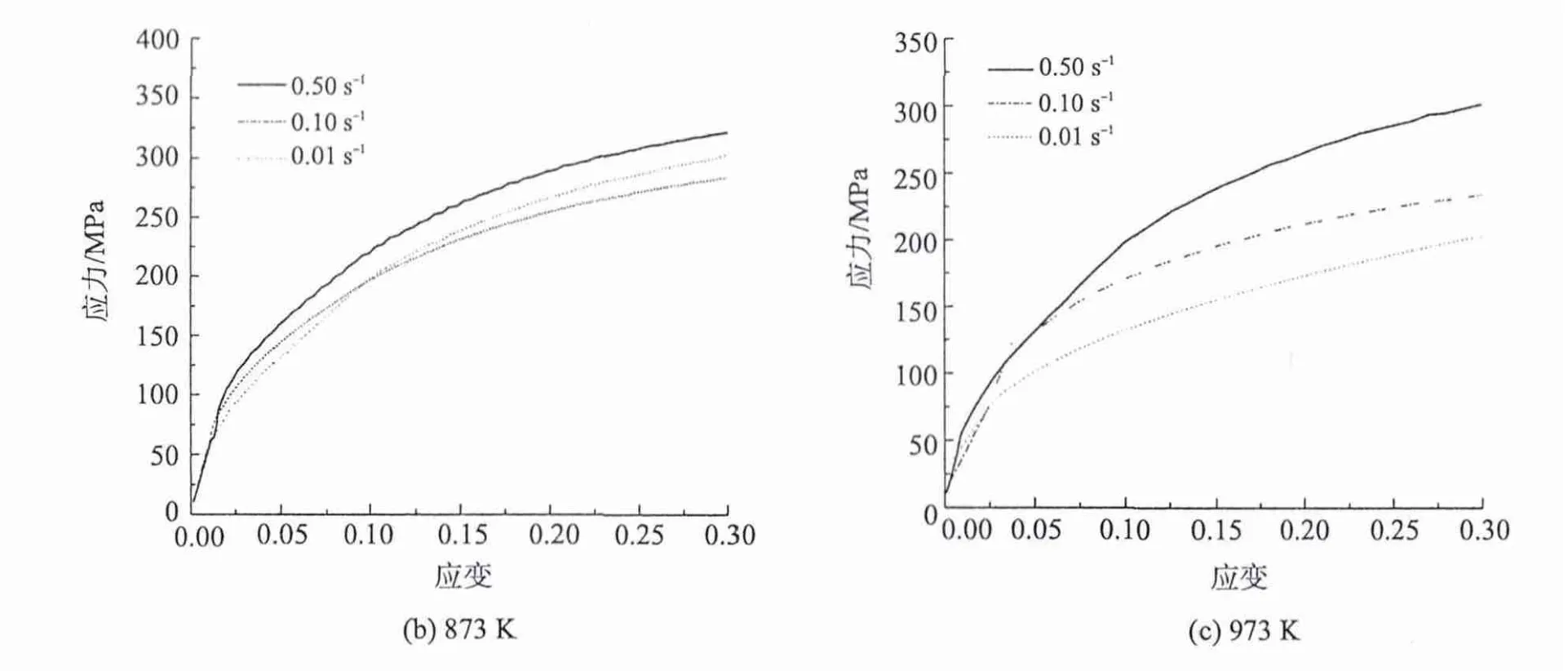
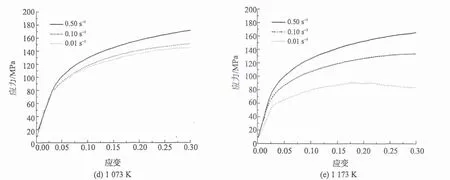
图1 不同温度下应力-应变曲线Fig.1 Stress-strain curve of hot stamping steel in different temperature
2.2 井上胜郎模型的修正
建立材料流变应力模型的方法大致为两大类:第一类是基于高温变形的实验结果,利用数理统计方法建立起的经验或半经验模型,该模型忽略了高温变形过程中内部组织的演化过程,主要考虑流变应力与变形工艺参数之间的关系,形式简单、精度较高、容易应用;第二类是从高温变形的物理机制出发建立起来的物理模型,此模型考虑了高温变形过程中的微观组织演化,如位错的迁移、动静态回复和再结晶等[8]。文中选取第一类方法中典型的井上胜郎材料模型,综合考虑变形温度、应变速率和变形程度的影响,适用范围较广。
在热变形过程中,应力σ与变形温度T、变形速率ε˙和应变ε有关,根据井上胜郎本构方程

式中:K,β为材料强度系数;n为应变硬化指数;m为应变速率敏感指数。
热成型钢板料热冲压成型数值模拟时需要提供不同温度下的流变应力模型,即确定不同温度下的应变硬化指数n值、应变速率敏感指数m值以及材料强化指数K和β值,因此需通过曲线拟合的方法,导出该热成型钢在热成型条件下以温度T和变形速率ε˙为自变量的变形性能参数的连续性函数表达式。对式(1)两边取自然对数得

由式(2)可知,当温度T和变形速率ε˙一定时,lnσ与lnε成线性关系,当应变在0.086~0.142之间时,lnσ与lnε的关系如图2,图中n值为直线的斜率,拟合后求得n值为0.342。当应变为0.15时,lnσ与lnε˙的关系如图3,m值为图中直线的斜率,拟合后可以求出m值,为0.043。lnσ与1/T的关系如图4,β值为图中直线的斜率,拟合后可以求出β值,为3 041.65。
将n=0.342,m=0.043,β=3 041.65代入式(2),求得lnK为2.96。由此,式(1)可表示为
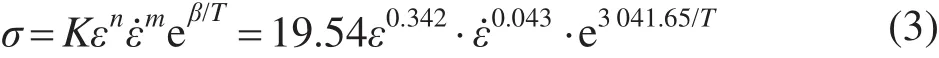
973,1 073 K条件下热成型钢热压缩实验结果与拟合结果如图5。采用井上胜郎模型对本文的数据进行回归分析,973,1 073 K条件下曲线拟合相关系数分别为0.947和0.958,而王立影[8]所求本构模型与实验结果数据的拟合相关系数为0.953,两模型拟合精度较为相近,基本能够表示出该热成型钢高温成型时的本构关系。为了在数值模拟中得到准确的结果,对井上胜郎本构方程的相关系数进行修正。从图2~4分析可得n值随温度升高而减小,m值随温度升高而增大,β值随应变速率增大而增大,对热模拟实验结果数据进行回归分析可得修正后的热成型钢热流变应力数学模型为

图2 lnσ与lnε的关系Fig.2 Relationship between lnσ andlnε

式中:a为温度对n值的影响系数;b为应变速率对n值的影响系数;c为温度对m值的影响系数;d为应变速率对m值的影响系数;f为应变速率对β值的影响系数;g为温度对β值的影响系数。
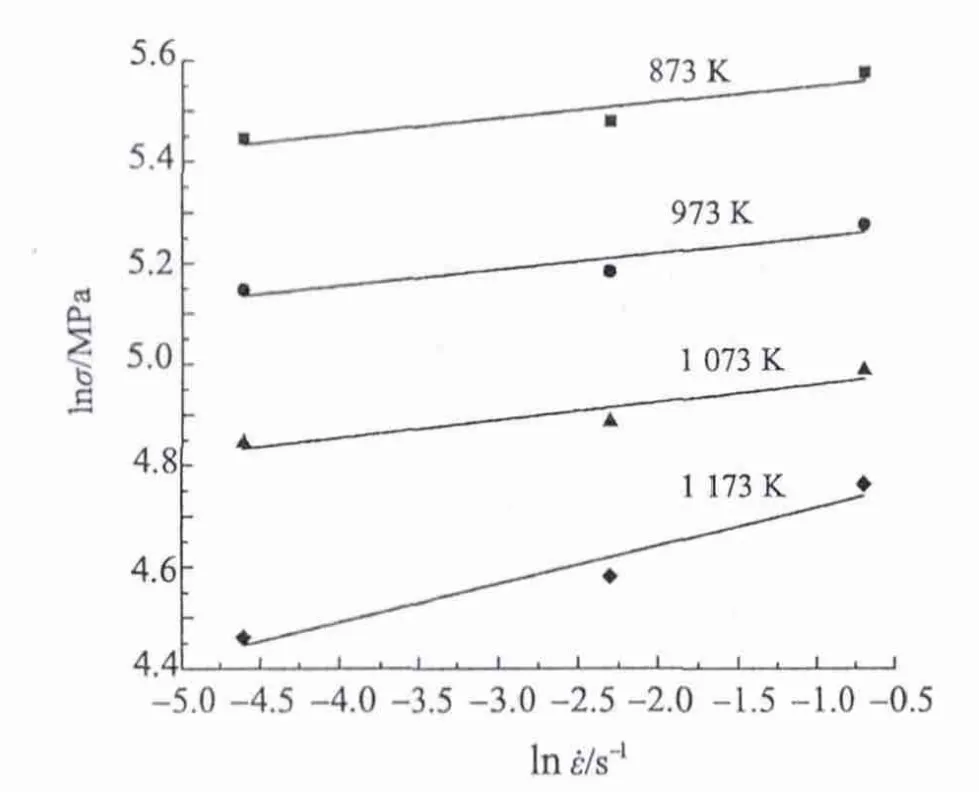
图3 lnσ 与 lnε˙的关系 (ε=0.15)Fig.3 Relationship between lnσ andlnε˙(ε=0.15)

图4 lnσ与 1/T的关系Fig.4 Relationship between lnσ and1/T
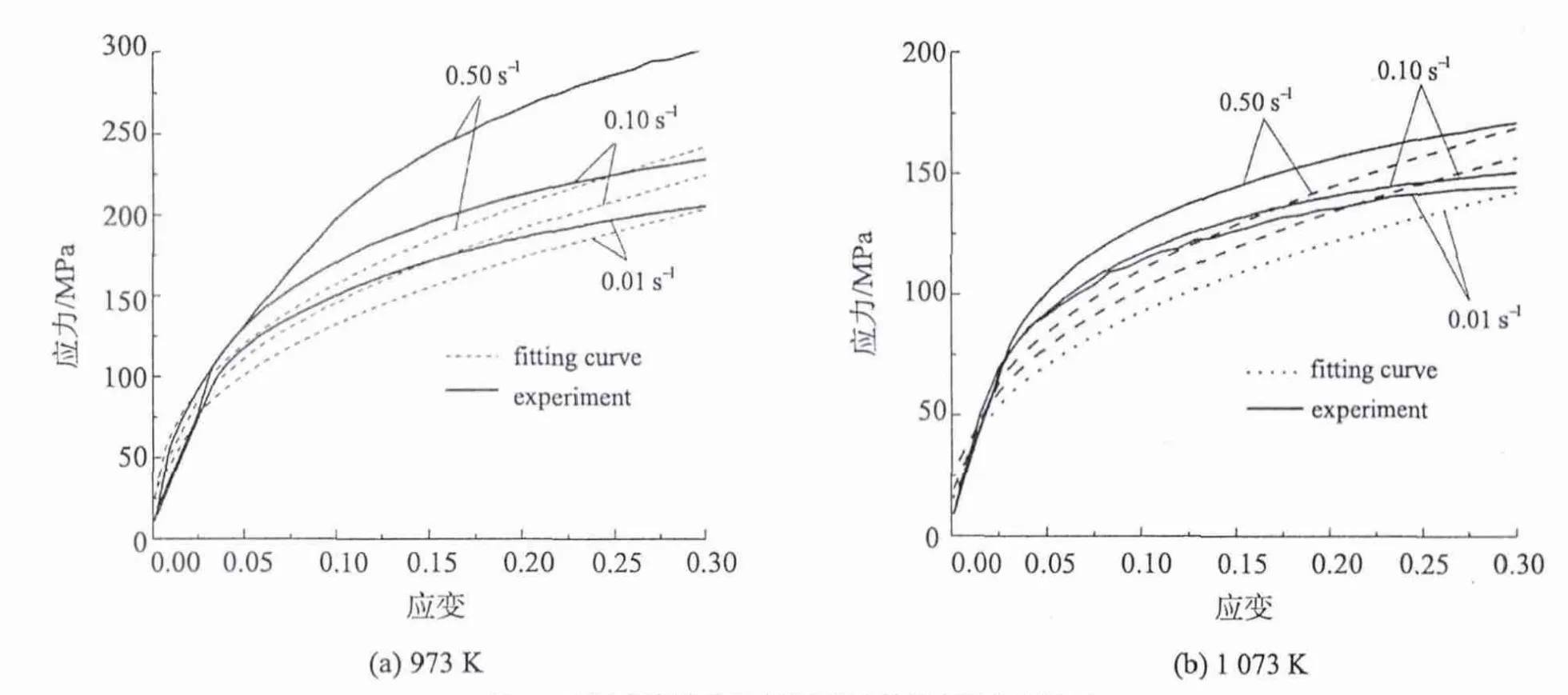
图5不同应变速率下的模型计算值与实验值比较Fig.5 Comparisons between simulated values and experiment values under different strain rates
由热模拟实验数据的方差分析可知,温度和应变的交互作用大于温度和应变速率的变互作用,故保留n关于T的线性关系,m,β作简化处理,得到3种修正流变应力模型,见表3。

表3 修正的流变应力模型对比Tab.3 Comparing with the mathematic models
对比表3中3种流变应力模型发现,模型1与模型3拟合相关系数较大,而模型3的表达式较为简洁,易于在模拟过程中计算分析。故文中建立热成型钢修正后的流变应力数学模型
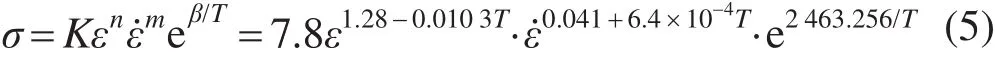
修正后的流变应力模型(井上胜郎模型)即为热成型钢板材热压缩时的本构方程,方程中n,m,β包括了温度及应变速率变化的影响。修正后的流变应力模型在温度为1 073 K时的应力应变的拟合结果如图6。比较图5(a),图6可见,该模型在均匀变形阶段导出的结果与实验结果更吻合,较修正前的模型拟合精度有较大提高。
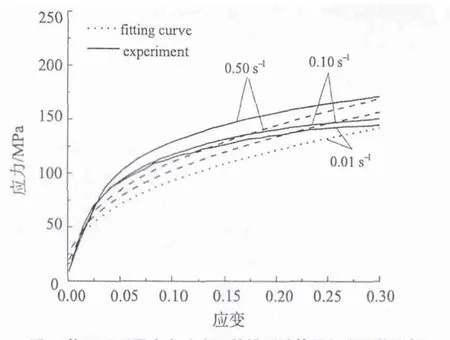
图6 修正后不同应变速率下的模型计算值与实验值比较Fig.6 Comparisons between simulated values and experiment values under different strain rates
3 结 论
1)热成型钢变形温度升高流变应力减小,应变速率增大流变应力增大;在低应变速率下,应力随应变的增加迅速上升,当达到一定的应变后,应力基本不变,此阶段由于热成型钢发生了动态回复和动态再结晶,从而产生软化。
2)新开发的热成型钢在高温压缩时的井上胜郎本构模型为σ=Kεnε˙meβ/T,其中K=19.54,n=0.342,m=0.043,β=3 041.65。修正模型参数n,m,β后,得到更加精确的本构模型,拟合相关系数为0.980,这为该热成型钢有限元数值分析提供了准确的材料模型。
[1]Lin J P,Wang L Y,Tian H B,et al.Research on the hot stamping process of quenchable ultrahigh strength steel[C]//Proceedings of the 2007 International conference onAdvances in Construction Machinery and Vehicle Engineering.Shanghai,2007:179-183.
[2]Masayoshi S,Kazuhisa K,Jun M,et al.Properties of aluminium coated steels for hot-forming[R]//Nippon Steel Technical Report 2003(88):18-21.
[3]Garcia Aranda L,Chastel Y,Fernandez Pascual J.Modelling hot stamping of quenchable steels[C]//5th International ESAFORM Conference on Material Forming.Krakow,2002:37-45.
[4]权国政,刘克威,王凤彪,等.7075铝合金热压缩动态软化行为的本构模型[J].机械工程材料,2010,34(10):82-86.
[5]林建平,王立影,田浩彬,等.超高强度钢热流变行为[J].塑性工程学报,2009,16(2):180-183.
[6]李辉平,赵国群,贺连芳,等.热冲压硼钢B1500HS高温本构方程的研究[J].机械工程材料,2012,48(8):21-26.
[7]杨小红,张士宏,王忠堂,等.AerMet100超高强度钢热变形行为[J].塑性工程学报,2007,14(6):121-126.
[8]王立影.超高强度钢板热冲压成形技术研究[D].上海:同济大学机械工程学院,2008.
