非线性药物动力学参数的计算方法研究进展

蔡 晔，孙春萌，沈 雁

（1.南京先声东元制药有限公司，江苏南京211800；2.中国药科大学药剂学教研室，江苏南京210009）

·综 述·

非线性药物动力学参数的计算方法研究进展

蔡 晔1，孙春萌2，沈 雁2

（1.南京先声东元制药有限公司，江苏南京211800；2.中国药科大学药剂学教研室，江苏南京210009）

目的旨在让药学领域的学者对非线性动力学参数的计算方法有更多的了解。方法本文综述了近年来有关非线性药物动力学的研究概况，介绍和评价了非线性药物动力学参数的计算方法及其应用。结果本文为研究非线性药物动力学参数的计算方法引入新思路。结论非线性药物动力学参数的计算方法推动了药物动力学更好的完善和发展。

非线性；药物动力学；参数；计算方法

药物动力学（pharmacokinetics）主要用于：①建立监测个体的体内药量或药物浓度随时间变化的数学表达式，并求算出有关药动学参数；②应用上述动力学模型、表达式和药动学参数，制定和调整个体化的用药方案，保证药物治疗的有效性和安全性［1］。药物动力学包括线性和非线性两大部分，前者发展较早，乃是经典部分，而后者则是现代药物动力学的重要进展。非线性药动学是指药物代谢动力学参数随剂量（或体内药物浓度）而变化的代谢过程（如生物半衰期）与剂量有关，又称剂量依赖性动力学。它不遵守简单的一级动力学过程，而遵从Michaelis－Menten方程；药物的消除半衰期随剂量的增加而延长；血药浓度－时间曲线下面积（AUC）与剂量不成正比，当剂量增加时，AUC显著增加；平均稳态血药浓度也不与剂量成正比。实际上，几乎所有药物都存在一定程度上的非线性过程［2］。

人类50年计算科学发展的重大突破之一是非线性拟合理论的建立与应用。药物动力学家在非线性拟合理论的完善与应用上做出了巨大的贡献。而非线性拟合也正是非线性药动学模型参数问题得以求解的关键技术之一［3，4］。国内外大多数药动学应用程序多采用加权非线性最小二乘法进行曲线拟合，以迅速计算出精确、合理的药动学参数。非线性药动学参数的计算方法大致分为主要有求导类算法和非求导类算法两种。前者主要包括：Gauss－Newton、Levenberg－Marquardt和Hartley等［5～7］，其中Marquardt和Hartley最为常用。后者主要包括单纯形算法（Simplex）、遗传算法、非线性混合效应模型法、人工神经网络和随机过程法等。

1 求导类算法

一般的非线性回归模型可以表示为：

式中，f（X）＝（f1（X），f2（X）……fn（X））′，是由n个X的非线性函数组成的n×1的向量。

非线性模型相应的误差方程为：

残差平方和为：

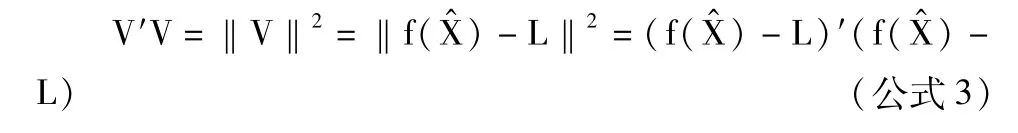
1.1 Gauss－Newton算法 Gauss－Newton的基本出发点就是在初值X（0）处对非线性模型进行线性近似，并按传统的平差方法求出一次近似值X（1），然后反复迭代，直至前后两次V′V值相等。

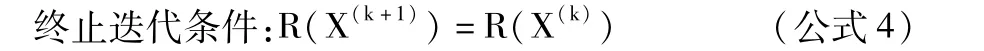
Gauss－Newton具有一定的合理性。如果（公式1）是线性模型，则由Gauss－Newton从任意值出发，经一次迭代就可得到最小二乘估计的精确解。当非线性模型（公式1）的非线性强度较弱时，Gauss－Newton是较好的方法。

1.2 Hartly算法 Gauss－Newton算法对初值的依赖性较强，当初值较差时易发散。为了克服这个缺点，提出了Hartly算法。当Gauss－Newton算法求出dX（k）后，若适当选取λ（k），使：

则一定有：V′V（X（k－1））＜V′V（X（k））。这样就能保证V′V（X（k））逐步向V′V的极小值靠近。于是就可避免迭代过程中的波动性，从而保证得到收敛的非线性最小二乘估计。Hardy算法除具备Gauss－Newton的全部优点外，还在很大程度上克服了Gauss－Newton强烈依赖初值的缺点，是一种很有实用价值的方法。几乎所有的药物动力学程序都包含了此算法。

1.3 Levenberg－Marquardt算法（LM，Marquardt） Gauss－Newton和Hardy求解的必要条件是B（X（k））矩阵列满秩。另外，当非线性模型（公式1）中存在复共线时，尽管 B（X（k））矩阵列满秩，但B′（X（k））B（X（k））的条件数很大，使B′（X（k））B（X（k））成病态。这时Gauss－Newton和Hartly算法无法应用。为了克服Gauss－Newton和Hardy的致命弱点，可以采用增大B′（X（k））B（X（k））主对角线元素的办法。

LM算法具有Steepest算法和Gauss一Newton的特点。对于秩亏非线性模型，采用LM最为有效。大多数药物动力学程序中LM都为首选算法。可见其地位与作用。求导类非线性拟合算法中还有Guass，Quasi－Guass，Steepest等算法。这些算法与Guass－Newton，Hartly，LM相比没有什么优势。

2 非求导类算法

非求导类算法其主要特点是无需根据目标函数推导导数方程。这样对于计算和程序设计方面相对于导数类算法容易实现。这一类算法主要包括了Simplex，SAA，GA和网格搜索等算法。

2.1 遗传算法（GeneticAlgorithm，GA） 遗传算法（GeneticAlgorithm，GA）［8，9］是以自然选择和遗传理论为基础，将生物进化过程中适者生存规则与群体内部染色体的随机信息交换机制相结合的高效全局寻优搜索算法。GA摒弃了传统的搜索方式，模拟自然界生物进化过程，采用人工进化的方式对目标空间进行随机优化搜索。它将问题域中的可能解看作是群体的一个个体或染色体，并将每一个个体编码成符号串形式，模拟达尔文的遗传选择和自然淘汰的生物进化过程，对群体反复进行基于遗传学的操作（遗传交叉和变异）。根据预定的目标适应度函数对每个个体进行评价，依据适者生存、优胜劣汰的进化规则，不断得到更优的群体，同时，以全局并行搜索方式来搜索优化群体中的最优个体，以求得满足要求的最优解。李进文等［10］用MATLAB 7.0所带遗传算法与直接搜索工具箱（GADS）或免费遗传算法最优化工具箱GAOT求得PK参数估计值。结果表明GA与常用PK软件包（传统算法）计算比较，结果基本一致，各有优点与不足之处。

2.2 改进单纯形算法（Simplex） 单纯形法是应用规则的几何图形，通过计算单纯形顶点的函数值，再根据函数值大小的分布来判断函数变化的趋势，然后按一定的规则搜索寻优的方法［11，12］。是按给定方案逐步搜索，直接比较目标函数的大小来寻求其极小值点的一种方法。单纯形是指以t维空间中的t＋1个点作为顶点所构成的超多面体。其原理如下：

对于非线性模型中的t个待估参数，按一定的规则选取t＋1组近似值，构成初始单纯形。用此t＋1组近似值计算t＋1个目标函数值并比较其大小。找出最大的目标函数值，并剔除相应的那组参数近似值。然后按一定的换点规则换入新的一组参数近似值。用这组新的近似值与其余的t组近似值构成新的单纯形。如此反复计算、比较、剔除，直至最小的目标函数数值以给定的精度逼近其极小值为止。这时与目标函数最小值相对应的那组参数近似值即为参数的非线性最小二乘估计。实现该原理首先要确定初始单纯形，然后要制定换点规则。该方法因步长固定，具有不能加速的缺点改进单纯形法是在单纯形法的基础上对步长作适当修改得到的寻优方法，在很多实际问题中应用广泛。董德元等［13］对单纯形法的计算过程做了详细阐述。吕庆文等［14］对单纯形法主要进行了两处改良，改良之一是：限制待定参数的边界值，有效地避免了不合理回归结果的出现；改良之二是：多次重构单纯形，即如果发生了多次压缩，则以当前单纯形中剩余平方和最小点为初值重新构建单纯形，从理论上推测可增加扩张的机会，减少收敛于局部的剩余平方和最小值的机会。其缺点是由于计算量增加。刘利斌等［15］基于改进的单纯形算法和残数法，对药物动力学房室模型中的有关参数计算进行了研究。通过实例表明，将改进的单纯形算法和残数法相结合得到的混合算法其计算精度高、收敛速度快、具有很好的稳定性。而且该算法对初值的选取要求不高，故有一定的实用价值。

综上所述，将残数法得到的计算值，作为改进单纯形法的初始值，然后求解一个无约束参数优化问题，所得药物动力学的二室模型拟合精度有明显的提高，且局部误差阶为0（10－3）。该结果说明了本文提出改进的单纯形算法与残数片两者相结合的方法，具有高精度的特点，同时又克服了改进的单纯形法可能由初始值选取所造成计算结果的不稳定性。因此，改进的单纯形法和残数法两者相结合的方法是适合药物动力学模型参数计算的。

对于常用非线性模型参数估计，大多采用变量代换的方法转化为线性模型，利用最小二乘法，求出模型参数。理论依据为残差平方和最小，由于使用了变量代换，因而计算出的回归方程不能保证残差平方和最小，甚至偏差很大。为了使基层工作者能正确简单地求出各模型参数，下面介绍几种简捷参数估计的新方法。

2.3 非线性混合效应模型法 非线性混合效应模型（nonlinearmixed effectmodel）亦称为多水平非线性模型。非线性随机效应模型或非线性分层模型，它可以解决非线性重复测量资料。不仅能识别和估计个体间和个体内的变异，而且也考虑了解释变量与反应变量参数间的非线性关系，允许固定效应和随机效应进入模型的非线性部分；非线性混合效应参数模型的反应变量可以服从正态分布（normal）、二项分布（bionomial）或泊松分布（poisson）；常用于药动学、非线性生长曲线、过度离散二分类资料等分析［16］。

Sheiner等［17］于1977年提出NONMEM（Nonlinear Mixed Effects Models）法。两阶段正态误差非线性混合效应模型是最简单的一种非线性混合效应模型，它不但能解决非线性的问题，也能解决线性的问题。与线性混合效应模型一样。非线性混合效应模型考虑了分布于不同层次上误差，给出相应的误差估计值；不严格要求时间间隔相等，在拟合个体曲线的同时也估计全部样本的曲线平均；对实际问题拟合曲线时，不要求每个个体有相同的测量点，即便有随机缺失值，也不增加拟合曲线的分析难度，仍可利用原资料提供的信息。非线性混合效应模型不仅考虑了参数间的非线性关系，允许固定效应和随机效应进入模型的非线性部分；且尚可在曲线中引入其他解释变量，如体重、组别等，分析其对代谢过程的影响。由于计算机应用的发展，复杂的非线性理论能得以实现，所以有关非线性理论的研究与探讨近来引起各界专家、学者广泛的关注。Botha等［18］用NONMEM法分析了南非79例新生儿使用庆大霉素的139个血药浓度数据。芮建中等［19］回顾性收集了745例门诊肾移植病人血药浓度数据1468个，用NONMEM程序估算PPK参数，并定量考察每日剂量、术后时间、体重、CYA剂型和合用药等固定效应对PPK参数的影响。最后拟合为米氏药代动力学模型。吴克华等［20］也通过对肾移植患者口服CYA的群体药动学研究，得出CL随着术后时间、总胆红素、年龄、红细胞比积的增加及肝药酶抑制剂的使用而下降，随着体重的增加而升高。Yukawa等［21］收集了349例儿童和成人苯巴比妥血药浓度数据648个，用NONMEM法分析后看出年龄对CL有影响，儿童的CL比成人大，大龄儿童的CL随体重增加而减低。

De Jongh等［22］用NONMEM法分析了抗癌药顺铂在成年癌症病人的3483个血药浓度数据，拟合为一室线性开放模型，并考察了年龄、性别、身高、体重、体表面积、血细胞比容、总蛋白、血肌酐清除率对清除CL及表观分布容积V的影响。Porta－Oltra等［23］用NONMEM法分析了5－氟尿嘧啶在大肠癌患者中的群体药动学，拟合为二房室一级消除模型。Takama等［24］用NONMEM法分析了30例接受造血干细胞移植前静脉输注白消安患者的群体药动学参数，共收集了690个血药浓度数据，拟合为一室模型，最终得出实际体重对CL及V的影响具有显著性，年龄对药代动力学参数的影响无显著性。Mougenot等［25］用NONMEM法分析了64例早期恶性肿瘤患者连续24 h输注苯丙氨酸氮芥的群体药动学特征。拟合为一房室模型。Bhattaran等［26］分别研究了抗心肌梗死药依尼泊胺及其代谢产物在健康自愿者及经过心肌再灌注治疗后的心肌梗死患者身上的群体药动学特征，他们分别收集了153例健康人静脉注射依尼泊胺的4 815个血药浓度数据及304例心梗患者的1 465个血药浓度数据，用NONMEM法求得最后参数并得出年龄对CL有影响肌酐清除率对V有影响。Mulla等［27］收集了英国79例儿童的160个氨茶碱血药浓度数据，拟合为一室一级吸收模型。Ramakrishna等［28］用NONMEM法研究了抗过敏，平喘药孟鲁司特静脉给药后在成人及6～14岁儿童体内的消除药代动力学，并考察了体重和年龄对参数的影响。结果显示体重对CL及V有影响，并得出6～14岁儿童静脉给药量为5～25 mg时最为合理的结论。

由于非线性混合效应模型理论较复杂，所以应用时尚需注意：①建立非线性方程。进行重复测量数据非线性模型拟合之前，要对原始资料作散点图，根据实测点的分布趋势、专业知识、过去经验建立一个适合变量间关系的非线性方程；必要时需借助其他软件，根据原始数据图给出粗略的模型表达式；②参数初始值的选择。尤在拟合模型复杂时，初始值选择不恰当，可能会出现迭代不收敛，或得到的参数估计局部最优，而不是全局最优等；③收敛准则和模型评价是非线性模型分析的重要内容，因此积累模型及初始值的选择经验、判断是否满足收敛条件及模型评价的标准是非线性分析的关键。

2.4 人工神经网络 神经网络（ncural nctwork，NN）或称人工神经网络（artificial nctural nctwoik，ANI′）是模拟生物的神经网络结构和功能而形成的一门数据分析的新方法学。神经网络方法的诞生可以追溯到20世纪40年代，中间经过几度起落。随着计算机科学的发展及其计算和处理能力的提高，近十几年国内外掀起研究和应用神经网络的高潮。而神经网络也已经应用到化学、生物学以及医学和药学领域。近几年来，神经网络也应用到药动学研究领域。神经网络是一种非线性动力学系统，具有强大的非线性处理能力。传统统计分析方法是以确定的统计模型为墓础，而实际上变量具有不确定性和时变性，变量间存在复杂的非线性关系，造成无法或很难精确建立模型，传统方法暴露出其局限性，而人工神经网络有表示任意非线性关系和学习的能力，给这些问题的解决提供了新的思想和方法。

人工神经网络可用于血药浓度和其它药物动力学参数的预测，与传统处理方法对比，人工神经网络准确度高，拟和度好。Yamanura等［29］利用患者的生理数据对氨基糖苷类药物的血浆药物浓度进行预测，对比了人工神经网络（ANN）和多元线性回归分析（MLRA）两种方法得到的预测值。结果表明，人工神经网络能辨别数据间的复杂关系，对抗生素血浆药物浓度的预测优于标准统计方法。周利锋等［30］对比了人工神经网络的回归模型和多元线性回归方程在预测分析上的差别，指出人工神经网络的预测模型比多元线性回归方程预测效果好，不仅r2大于多元线性回归方程，而且无需考虑协变量间是否独立、应变量是否满足正态分布等条件。Brier等［31］对比了人工神经网络与药动学非线性混合效应模型软件（NONMEM）对庆大霉素的峰谷浓度预测结果表明，人工神经网络能够更好地重现庆大霉素稳态血清峰浓度的分布情况。

2.5 基于系统理论（system approaches，SA）的随机过程法药动学研究的一般程序是：测定体内药物（代谢物）浓度，选择特定药动学模型，拟合实验数据，因此，这种参数仅相对于特定模型才有相应的意义。SA则从另一角度研究药动学。其基本思路是：确立1个（多个）一般的系统特性（system，property），用简单的经验方程（指数函数或曲线函数等）求得效应的近似解。这些经验方程参数不具备特定的药动学意义，但参数的集合可表示方程参数向量并给出效应的解。本法不需要先确立模型，所涉及的运算多为线性运算，因最终结果是效应近似解而不是参数估计值，可避免对各参数间相关、交异性等繁琐的数学分析。

近年来，随机过程在生物学研究中取得了一些进展，如种群生长、疾病——死亡过程等［32～34］，但该方法在药动学研究方面的应用，尚未见报道。SA有可靠、合理的药动学基础。比如，药物在体内转运、代谢、排泄均遵循随机概率原则，SA即根据该原则设计。假定药物分子由机体某一部位iv注射，该分子的体内过程主要取决于扩散和转运，已知药物扩散是一随机概率过程，在药物浓度较低时更是如此，且每一分子的扩散是独立的，不影响其他分子扩散。同样，药物在心血管系统转运、肾脏滤过及重吸收均为随机过程。

丁勇［35］尝试用随机过程方法探讨药物的动力学过程。机体是一个十分复杂的组织，药物在体内的时间过程可看成无数个药物分子在各种因素的综合作用下的随机转运过程，一般需要经过三个状态：首先药物进入体内的吸收部位（如胃肠道），相当于处于状态1；然后被逐步吸收，进入体循环（如经过血液循环分布至全身，相当于进入状态2；再通过消除器官（如肝脏、肾等）排出体外，相当于进入状态3。在上述一系列过程中，药物在体内完成相应的生理、生化功能，并达到一定的治疗效果。

SA是定量分析系统的一般特性，而不必具体描述或模拟某一个特别性的动力学过程。例如，预测血药浓度的叠加原理是SA方法中的一种，但如将叠加原理用于具体房室模型，由于药物配置被模型化，就不是SA了。同样，以剂量校正AUC计算生物利用度属于SA，而以Cmax、tmax定量药物吸收速率则不属于SA，因为对这两个变量与药物吸收间关系无法用数学式表达。本法一般仅涉及药动学函数而不是药动学参数，因为某些动力过程（如吸收），既不能用简单的动力学公式模拟也不能用参数表达。而SA求得百分吸收曲线较之Ka、tmax、Cmax、ta、F等参数信息量更丰富，况且这些参数对吸收过程的描述也不够完善。如有必要，SA也可求得一些参数，如达到某一百分吸收率的时间及由百分吸收曲线求出的生物利用度等。SA对药动学评价不依赖于模型且侧重于药物的非线性性质，而传统方法先假定模型，最终是对某一函数的分析，结果不能完全甚至不能近似地反映药物性质。SA不需提出假设和模型，SA对药物性质的分析较传统方法更客观、灵活，可防止陷入误区。但SA本质是非特异性的，故不能阐明各个过程的具体特征，因而不适用于对具体过程的动力学研究。

3 其他类算法

此外还有变尺度法（Variable Metric Method，又称类牛顿法），共轭梯度算法（Conjugate Gradient Method）［36］。这些算法都是十分优秀而有效的，但是并没有被广泛集成于药动学软件包中。希望药动研究者在未来的药动软件中见到这些算法知道它们的大致思想，以便于高效的进行药物动力学研究。

［1］梁文权.生物药剂学与药物动力学［M］.第3版.北京：人民卫生出版社，2000.

［2］Rowland M，Tucker G.Pharmcacokinetics：theory and methodology［M］.Oxford：Pergamon Press，1986.

［3］钟大放.药物代谢与药物动力学基础研究展望［J］.辽宁药物与临床，2000，3（4）：145－148.

［4］Meibohm B，Derendorf H.Pharmacokinetic／Pharmacodynamic studies in drug product development［J］.J Pharm Sci，2002，91（1）：18－31.

［5］D.M.贝茨，D.G.沃茨.非线性回归及其应用［M］.北京：中国统计出版社，1997.

［6］王新洲.非线性模型参数估计理论与应用［M］.武汉：武汉大学出版社，2002.

［7］WalterW.Ordinary differential equations［M］.New York：Springer 1998.

［8］雷英杰，张善文.MATLAB遗传算法工具箱及应用［M］.西安：西安电子科技大学出版社，2005.

［9］薛定宇，陈阳泉.高等应用数学问题的MATLAB求解［M］.北京：清华大学出版社，2004.

［10］李进文，陈朝辉，曾平，等.基于遗传算法的药物动力学参数估计［J］.数理医药学杂志，2006，19（5）：529－530.

［11］罗文广.一种改进的单纯形优化算法及其仿真研究［J］.计算机仿真，2003，20（10）：62－64.

［12］刘磊，王斌会，蔡湛宁，等.改良单纯形法和连续二次方程法对心肌酶代谢动力学一房室模型非线性回归的比较［J］.数理医药学杂志，1999，12（3）：214－215.

［13］董德元，杨节，等.试验研究的数理统计方法［M］.北京：中国计量出版社，1987.

［14］吕庆文，刘磊，钱学贤，等.单纯形法在医学回归分析上的应用与改进［J］.中国卫生统计，1994，11（1）：10－11.

［15］刘利斌，张文，谢竹诚.基于改进单纯形算法的药物动力学参数计算［J］.浙江科技学院学报，2007，19（1）：4－6.

［16］李珍，陈刚.群体药动学研究中非线性混合效应模型法的评价和应用［J］.国外医学（药学分册），1993，20（4）：195－199.

［17］Sheiner LB，Rosenberg B，Marathe VV.Estimation of population characteristics of pharmacokinetic parameters from routine clinical data［J］.J Pharmacokinet Biopharm，1977，5（5）：445－479.

［18］Botha JH，du PreezMJ，AdhikariM.Population pharmacokinetics of gentamicin in South African newborns［J］.Eur JClin Pharmacol，2003，59（10）：755－759.

［19］芮建中，曹学峰，李金恒，等.我国肾移植患者环孢菌素常规监测的群体药代动力学［J］.中国临床药理学杂志，2002，18（6）：431－437.

［20］吴克华，卢炜，李静，等.环孢菌素群体药动学的研究及应用［J］.中国药学杂志，2006，41（23）：1818－1821.

［21］Yukawa E，To H，Ohdo S，etal.Detection of a drug－drug interaction on population－based phenobarbitone clearance using nonlinearmixed－effectsmodeling［J］.Eur J Clin Pharmacol，1998，54（1）：69－74.

［22］de Jongh FE，Gallo JM，Shen M，etal.Population Pharmacokinetics of cisplatin in adult cancer patients［J］.Cancer Chemother Pharmacol，2004，54（2）：105－112.

［23］Porta－Oltra B，Perez－Ruixo JJ，Climente－Marti M，et al.Population pharmacokinetics of5－fluorouracil in colorectal cancer patients［J］.JOncol Pharm Pract，2004，10（3）：155－167.

［24］Takama H，Tanaka H，Nakashima D，et al.Population pharmacokinetics of intravenous busulfan in patients undergoing hematopoietic stem cell transplantation［J］.Bone Marrow Transplant，2006，37（4）：345－351.

［25］Mougenot P，Pinguet F，Fabbro M，et al.Population pharmacokinetics ofmelphalan，infused over a 24－hour period，in patients with advanced malignancies［J］.Cancer Chemother Pharmacol，2004，53（6）：503－512.

［26］Bhattaran VA，Nagaraja NV，Peters T，et al.Population pharmacokinetics of eniporide and its metabolite in healthy subjects and patientswith acutemyocardial infarction［J］.JClin Pharmacol，2005，45（6）：631－639.

［27］Mulla H，Nabi F，Nichani S，et al.Population pharmacokinetics of theophylline during paediatric extracorporeal membrane oxygenation［J］.Br JClin Pharmacol，2003，55（1）：23－31.

［28］Ramakrishnan R，Migoya E，Knorr B.A population pharmacokinetic model for montelukast disposition in adults and children［J］.Pharm Res，2005，22（4）：532－540.

［29］Yamamura S，Nishizawa K，Hirano M，et al.Prediction of plasma levels of aminoglycoside antibiotic in patients with severe illness by means of an artificial neural network simulator［J］.JPharm Sci，1998，1（3）：95－101.

［30］周利锋，金丕焕.神经网络与多元线性回归的比较［J］.现代预防医学，1998，25（3）：272－274.

［31］Brier ME，Zurada JM，Aronoff GR.Neural network predicted peak and trough gentamicin concentrations［J］.Pharm Res，1995，12（3）：406－412.

［32］蒋庆琅.随机过程原理与生命科学模型［M］.上海：上海翻译出版公司，1987.

［33］丁勇.马尔可夫链在生长发育研究中的应用［J］.数学的实践与认识，1990，2：6－9.

［34］徐克学.生物数学［M］.北京：科学出版社，1999.

［35］丁勇.药动学随机过程模型［J］.数学的实践与认识，2004，34（8）：77－80.

［36］William H.Press，et al，Numerical Recipes in C［M］.Cambrige：Cambrige University Press，1998.

Progress on pharmacokinetics parameters calculation of nonlinear models

CAIYe1，SUN Chun-meng2，SHEN Yan2
（1.Nanjing Simcere Dongyuan Pharmaceutical Co.，Ltd.，Nanjing 211800，China；2.Department of Pharmaceutics，China Pharmaceutical University，Nanjing 210009，China）

ObjectiveTo promote scholars in pharmacokinetics to know more about nonlinear characteristics and applications in the hope of contributing to the perfection and development of pharmacokinetics.MethodsRecent studies in the parameters calculation ofnonlinear pharmacokineticsmodelswere reviewed.ResultsTo bring the new ideas to investigate the nonlinear pharmacokinetic parameters calculated method.ConclusionThis research would promote the improvement and development of the the nonlinear pharmacokinetic parameters calculated method.

Nonlinear；Pharmacokinetics；Parameters；Calculation

R969.1

：A

2095－5375（2014）07－0401－005

中央高校基本科研业务费专项资金资助（项目批准号No.JKQ2011018）；国家自然科学基金资助项目（No.81201182）

蔡晔，女，副教授，研究方向：药物新剂型与新技术，E－mail：Caiye＠simcere.com

沈雁，女，副教授，研究方向：药物新剂型与新技术，Tel：025－83271305，E－mail：shenyan19820801＠126.com