基于变异田口算法的阵列天线方向图综合

杨 敏，田雨波，陈 风

(江苏科技大学电子信息学院，江苏镇江212003)

通信、雷达、遥感等领域通常会需求具有特殊性能的天线，很多时候单一的天线并不能满足要求.这时，可以采用多个天线按一定方式排列成天线阵列来解决问题［1］.根据给定的天线辐射方向图或者给定的对天线性能参量的要求来设计天线阵元的个数、阵元之间的间距、阵元上激励电流的幅值和相位分布，称为天线综合［2］.天线阵列综合问题中使用的比较经典的方法有切比雪夫多项式法、傅里叶变换法等［3］.这些传统的方法往往具有自己的既定规则，大多针对某一特定的问题，对于更复杂的具有约束条件的综合实例很难实现.对于形状复杂的大型天线阵列，虽然可以采用基于梯度寻优技术的传统数值优化方法，但由于天线最优化问题中往往存在多参数、非线性、不可微、不连续的目标函数或者约束条件，传统数值优化方法无法有效求得工程上满意的解［4］.因此，具有稳健性、随机性的智能优化算法，例如遗传算法(genetic algorithm，GA)、粒子群优化算法(particle swarm optimization，PSO)在复杂的非线性天线优化问题中得到了应用，如天线阵列稀疏［5］、降低最大旁瓣电平［6］、通过控制激励电流幅值或相位在干扰源方向生成零点［7］等.尽管上述文献中的粒子群优化算法是有效的，但其计算量大、效率不高，且容易陷入局部最优，丢失全局最优解［8］.为此，文中介绍了一种能有效降低计算量、快速收敛的全局优化算法田口算法(Taguchi method，TM)，该算法由日本的田口玄一博士在20世纪70年代提出，起初是一种在质量工程中应用的实验设计方法［9］.尽管田口算法已经被广泛应用于诸多领域，如化工［10］、机械工程［11］、电力电子［12］等行业，但在电磁领域的应用还不是很多，仅仅只有少数的实例.例如文献［13］将田口算法与FDTD相结合，为超宽带TEM喇叭天线及其阵列的优化提供了一种有效的方法.文中研究田口算法在天线方向图综合上的应用，验证了它在电磁优化方面巨大的潜能.

田口算法最突出的一个特点是基于正交表对参数空间的均匀抽样，因此能够有效降低实验次数，达到快速收敛的目标［14］.但其缺少跳出局部极值的机制，容易陷入局部最优.为了使田口算法能够实现更复杂的设计目标，例如在降低旁瓣电平的同时，还要在特定方向形成零点，文中在田口算法基础上进行了适当的改进，设计了一种基于变异算子的田口算法(mutation-based Taguchi method，MTM).同时，加入了自适应内循环机制，多样化搜索空间的同时尽量减少算法迭代次数，保证算法执行效率.

1 算法描述

1.1 基本田口算法

田口算法之所以能够降低计算量、快速收敛，依赖于两个关键技术，一是正交表，二是信噪比.以10个参数且每个参数有3个水平值为例，采用完整排列实验需要进行310=59049次实验，用正交矩阵来设计实验，则只需要进行27次实验.对27次实验的输出结果进行简单的统计处理后，就可以得到一个最优的参数值组合.尽管实验的数量大幅减少，但从正交矩阵获得的最优结果和从完整排列方法获得的最优结果是接近的.而信噪比概念的采用则可以增大适应度函数值之间的差异，有效的评估参数水平值组合的优劣.

假设使用正交表OA(N，k，s，t)来设计各参数水平值的组合(文中以水平s取3为例).第n个参数在第i次迭代时的m水平值用表示.初始参数2水平值设置为参数搜索空间(Xmin，Xmax)的中间值，其余各代取父代最优解.和分别由式(1，2)确定:

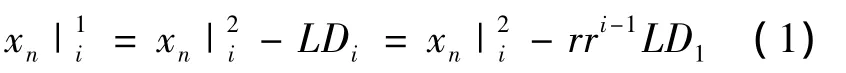
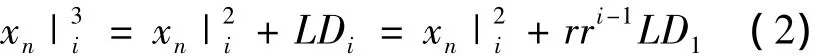
式中:rr∈(0，1)为指数衰减因子.初始水平差值LD1由式(3)确定:

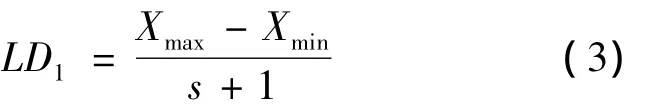
根据各组实验的参数水平值组合计算适应度函数值Fitness，并由式(4)计算信噪比h:

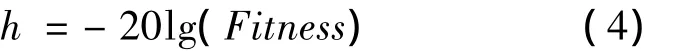
由式(5)得到每个参数、每个水平的平均信噪比:

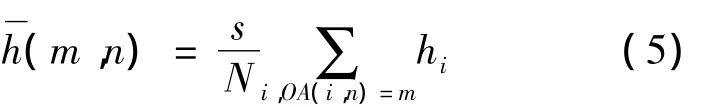
1.2 基于变异机制的田口算法

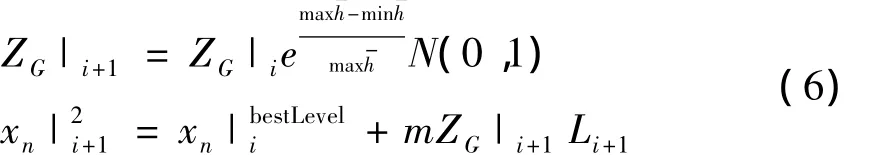
式中:ZG为变异步长;Z;max为对应参数当前最大平均信噪比;min为对应参数当前最小平均信噪比，max越大，ZG越大，可以有效阻止算法过快收敛，陷入局部最优;N(0，1)为服从标准正态分布的随机变量表示当前最佳参数水平值组合;0＜m＜1为二级变异步长，调节变异强度;Li+1为参数搜索空间.

变异田口算法的流程如图1.

变异田口算法步骤如下:

1)根据优化参数个数，选择合适的正交表OA，设计合适的适应度函数Fitness、衰减因子rr、最大内循环次数Nin和最大迭代次数M;

3)根据参数表OA_para进行实验，计算适应度函数值和平均信噪比，并构造反馈表;

5)判断内循环次数是否达到Nin，达到则执行下一步，否则，进行变异操作，转到步骤2);

6)判断是否达到最大迭代次数M，未达到则缩小水平差值，进行变异操作并转到步骤2)，否则执行下一步;

7)结束程序，保存结果.

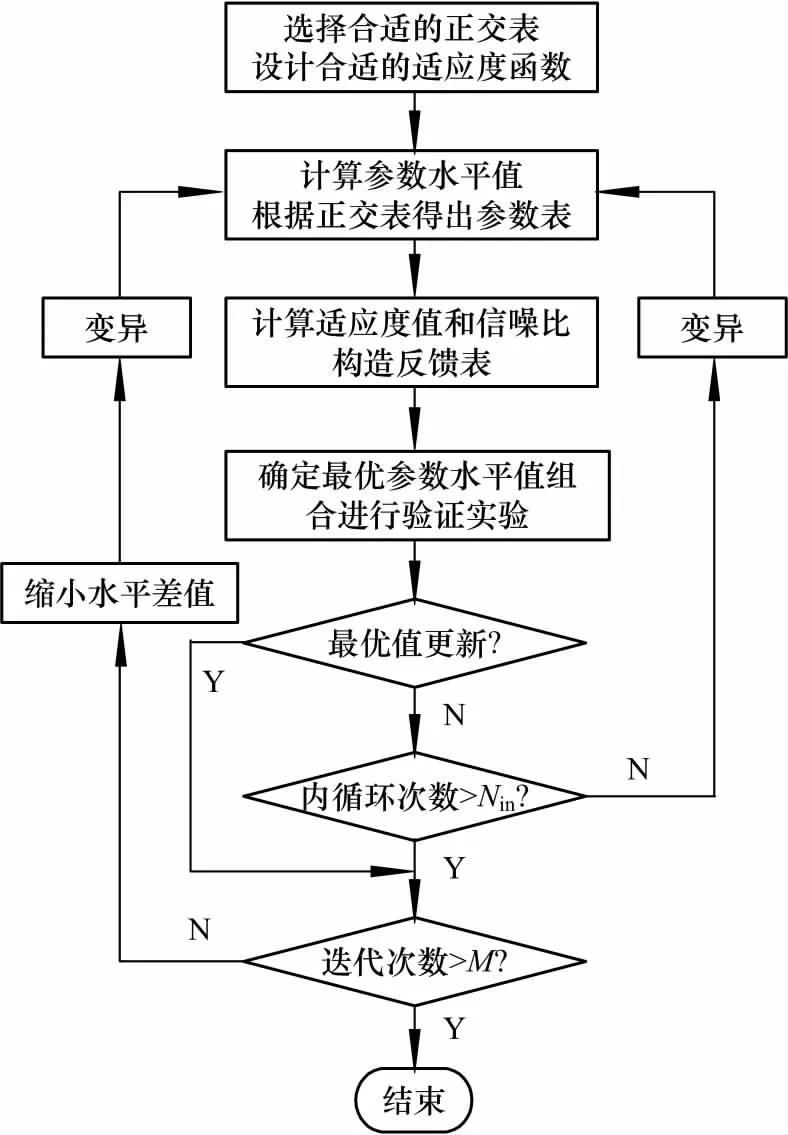
图1 变异田口算法流程Fig.1 Flow chart of MTM

变异田口算法中的变异操作以父代最优解为中心，服从正态分布，保证了算法的计算精度.同时加入内循环机制，使得当前水平差值下每进行一次循环就按照变异公式产生一组参数表，多样化了参数搜索空间.只要结果优于当前最优解，就跳出内循环.如果内循环达到设定的最大次数还未找到优于当前最优解的值，也跳出内循环并缩小水平差值，进行下一步迭代操作，有效控制了算法的迭代次数，保证了算法的效率.

2 阵列天线方向图综合

2.1 初始化

算法的初始化包括选择适当的正交表和设计合适的适应度函数.正交表的选择由需要优化的参数个数决定，适应度函数由设计目标决定.

1)正交表

文中使用的优化案例参数个数有10和20两种.用田口算法及变异田口算法优化时，若参数个数为 10，则选择正交表OA(27，10，3，2);若参数个数为 20，则选择正交表OA(81，20，3，2).一般来说，可以提高正交矩阵的强度t来考虑参数之间的相互作用.然而，强度t越大，正交矩阵的行数就越多，文中的优化案例使用强度为2、水平数为3的正交表就足够了.

2)适应度函数

设一个阵元数目为2N=20的直线阵(图2)，阵元沿着z轴均匀排列，且关于x轴对称分布，相邻两阵元间的距离为d.第n个阵元的激励电流为In=anejφn.

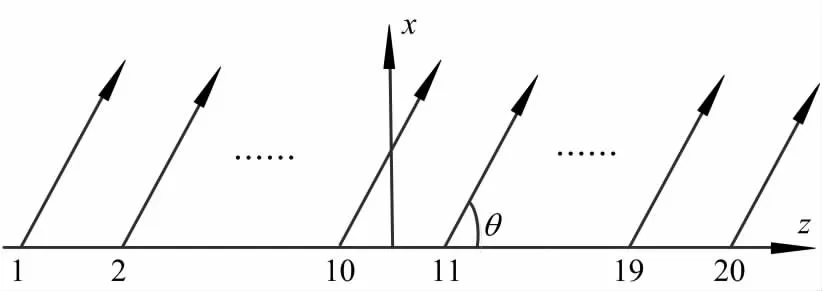
图2 直线阵示意图Fig.2 Schematic diagram of linear array

由方向图乘积定理可知，忽略阵元间的互耦影响，相同且取向一致的阵元组成的阵列方向图可以由阵元方向性函数乘以阵的方向性函数得到.则天线阵在远区的辐射总场可以表示为:

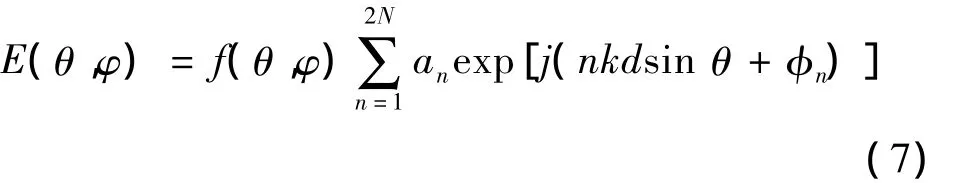
式中:an为激励电流的幅值;φn为激励电流的相位;θ为空间辐射角为波数.当f(θ，φ)=1时，得到阵列的总场方向性函数:

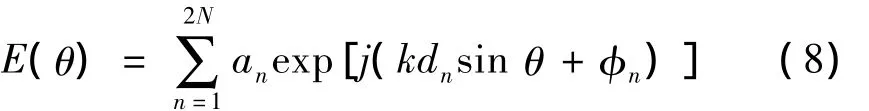
为了方便解决问题，常常将方向性函数进行归一化处理，得到归一化方向性函数:

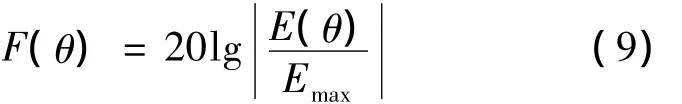
采用式(10)作为适应度函数进行优化:

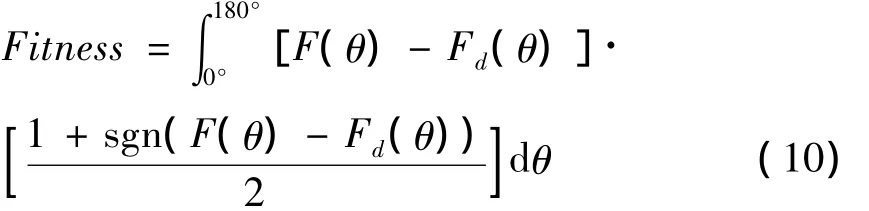
式中:F(θ)为式(9)的计算值;Fd(θ)为目标值.

2.2 优化激励电流幅值

1)低旁瓣方向图综合

设计要求主瓣对准90°方向，零功率波瓣宽度为 20°，最大旁瓣电平(maximum side lobe level，MSLL)为 -30dB.相邻阵元间的距离d取0.5λ，激励电流的相位均为0.由于阵列关于x轴对称分布，因此只需优化10个阵元的激励电流幅值，电流幅值an的取值范围为［0，1］.采用式(10)作为适应度函数，分别用PSO、田口算法、变异田口算法进行优化.PSO算法中种群数目设置为25，最大迭代次数设置为200;田口算法、变异田口算法选择正交表OA(27，10，3，2)进行实验，衰减因子设置为0.75;田口算法中收敛限制设置为0.002;变异田口算法中最大迭代次数设置为50.用PSO、田口算法及变异田口算法进行低旁瓣方向图综合得到的MSLL及适应度函数总计算次数(total count，TC)如表1，得到的天线波束方向图如图3，其中归一化方向回增益为F(θ)，辐射角度为θ.各阵元的激励电流幅值如表2.

由表1及图3中可以看出，与PSO相比，田口算法优化后MSLL降低了1.8dB左右，变异田口算法优化后MSLL降低了2.5dB左右.并且利用田口算法和变异田口算法优化时，适应度函数总计算次数远远小于PSO.虽然与田口算法相比，使用变异田口算法优化计算量增加了，但它取得了更好的优化结果，达到了设计的要求.与PSO相比，变异田口算法实验的减少量在70%左右，显然，对于解决这个问题并且达到目标，变异田口算法比PSO更快更好.

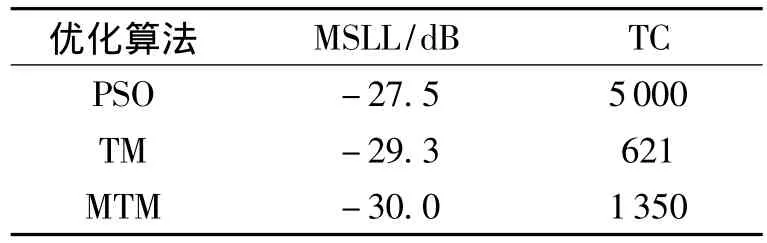
表1 PSO、田口算法、变异田口算法优化得到的MSLL及TCTable 1 Optimized MSLL and TC by using PSO，TM and MTM

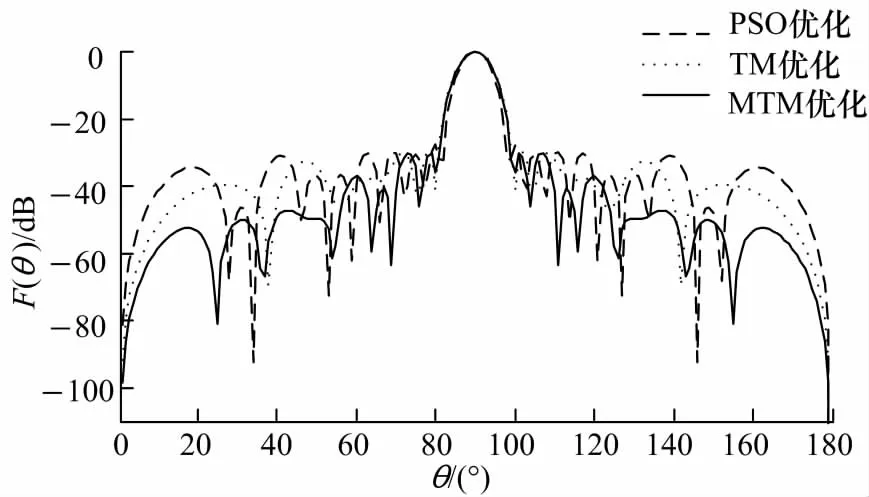
图3 PSO、田口算法、变异田口算法综合低旁瓣方向图Fig.3 Low side lobe beam pattern synthesis using PSO，TM and MTM

表2 用PSO、田口算法、变异田口算法优化得到的激励电流幅值Table 2 Optimized magnitudes of excitation current by using PSO，TM and MTM

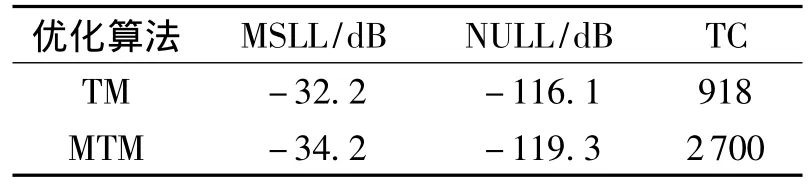
表3 田口算法、变异田口算法优化得到的MSLL，NULL及TCTable 3 Optimized MSLL，NULL and TC by using TM and MTM

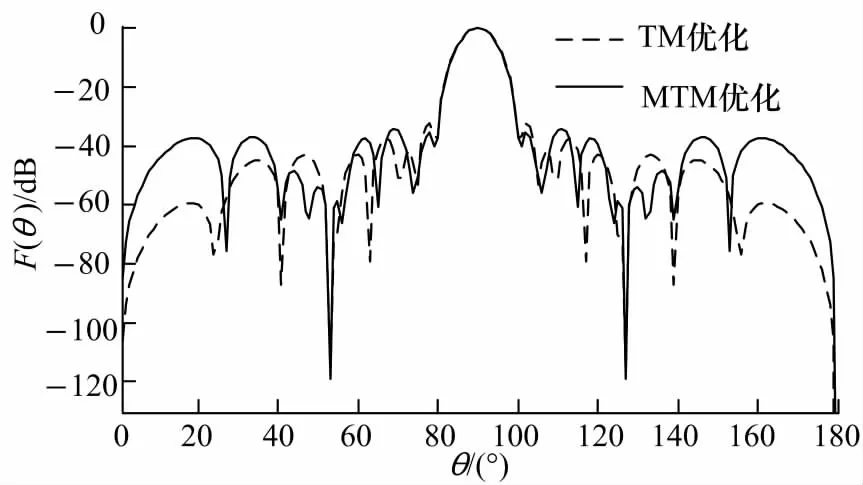
图4 田口算法、变异田口算法综合具有单零点的方向图Fig.4 Antenna array pattern synthesis with deep null using TM and MTM

2)具有零陷的方向图综合

首先讨论单个零陷情况.设计要求主瓣对准90°方向，零功率波瓣宽度为20°，MSLL为 -30 dB，53°方向形成零陷.相邻阵元间的距离d设置为0.5λ，激励电流的相位均为0，仍只需优化10个阵元的激励电流幅值，电流幅值an的取值范围为［0，1］.采用式(10)作为适应度函数，分别用田口算法、变异田口算法进行优化.田口算法、变异田口算法选择正交表OA(27，10，3，2)进行实验，衰减因子设置为 0.81;田口算法中收敛限制设置为0.001;变异田口算法中最大迭代次数设置为100.用田口算法及变异田口算法综合具有单个零陷的方向图得到的MSLL、零陷深度(NULL)及TC如表3，两种算法综合得到的波束方向图如图4，得到的激励电流幅值如表4.

由图4及表3中的数据可以看出，与田口算法相比，虽然用变异田口算法进行优化使得适应度函数计算次数增加了，但是优化后的MSLL降低了2.0 dB左右，零点深度加深了3.2 dB.以少量的迭代次数为代价，取得更好的优化结果是可取的.

表4 用田口算法、变异田口算法优化得到的激励电流幅值Table 4 Optimized magnitudes of excitation current by using TM and MTM

再讨论多个零陷情况.设计要求53°及65°方向形成零陷.田口算法、变异田口算法衰减因子设置为0.86;田口算法中收敛限制设置为0.001;变异田口算法中最大迭代次数设置为150，其余设置与上文单个零陷方向图综合一致.用田口算法及变异田口算法综合多零陷方向图得到的MSLL及TC如表5中，得到的波束方向图如图5，得到的激励电流幅值如表6.

表5 田口算法、变异田口算法优化得到的MSLL、NULL及TCTable 5 Optimized MSLL，NULL and TC by using TM and MTM

由图5及表5中的数据可以看出，与田口算法相比，变异田口算法优化后MSLL降低了2.0dB左右，53°和127°方向零点深度降低了30.0 dB左右，65°和115°方向零点深度降低了27.1 dB左右.变异田口算法的适应度函数计算次数虽然增加了，但在可接受范围之内.

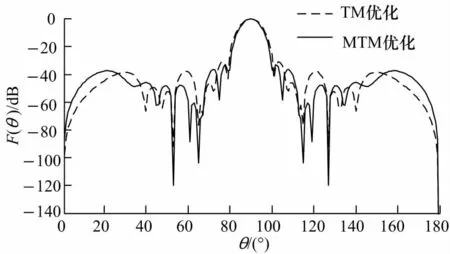
图5 田口算法、变异田口算法综合具有多个零点的方向图Fig.5 Antenna array pattern synthesis with nulls using TM and MTM

表6 用田口算法、变异田口算法综合多零点方向图得到的激励电流幅值Table 6 Optimized magnitudes of excitation current of beam pattern synthesis with deep nulls using TM and MTM

2.3 优化激励电流幅值和相位

设计要求主瓣对准90°方向，零功率波瓣宽度为20°，MSLL为 -30 dB.相邻阵元间的距离d取0.5λ.优化10个阵元的激励电流幅值及相位，电流幅值an的取值范围为［0，1］，相位φn的取值范围为［0，2π］.仍选择公式(10)作为适应度函数，分别用田口算法、变异田口算法进行优化.田口算法、变异田口算法选择正交表OA(81，20，3，2)进行实验，衰减因子设置为0.84;田口算法中收敛限制设置为0.002;变异田口算法中最大迭代次数设置为60.两种算法优化得到的MSLL及适应度函数总计算次数如表7，两种算法优化得到的波束方向图如图6，用田口算法及变异田口算法综合低旁瓣方向图得到的电流幅值和相位如表8.

由表7及图6可以看出，在适应度函数总计算次数未大幅增加的情况下，变异田口算法优化得到的MSLL比田口算法优化得到的降低了0.3 dB左右，达到了设计要求.

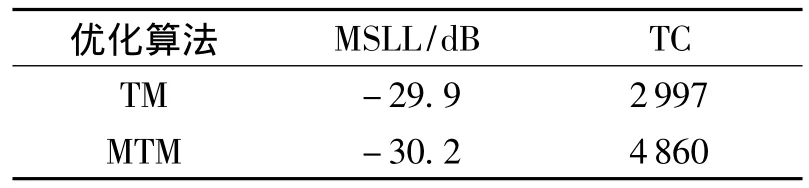
表7 田口算法、变异田口算法优化得到的MSLL，NULL及TC Table 7Optimized MSLL，NULL and TC using TM and MTM

图6 田口算法、变异田口算法综合低旁瓣方向图Fig.6 Low side lobe beam pattern synthesis using TM and MTM

表8 用田口算法、变异田口算法综合低旁瓣方向图得到的激励电流幅值和相位Table 8 Optimized magnitudes and phases of excitation current of low side lobe beam pattern synthesis using TM and MTM

3 结论

文中研究了变异田口算法在直线阵方向图综合中的应用，成功的获得了具有低旁瓣及特定方向产生零点的方向图，验证了变异田口算法的有效性.与智能优化算法PSO相比，变异田口算法不仅大大提高了效率，且优化结果更好.变异田口算法具有易实施、高效率，低计算量的特点，在其他电磁优化应用中具有广泛的应用前景.

References)

［1］ 茂光.阵列天线分析与综合［M］.电子科技大学出版社，1989.

［2］ Elliott R S.Array pattern synthesis［J］.Antennas and Propagation Society Newsletter，IEEE，1985，27(5):4-9.

［3］ 王新宽，焦永昌，谭艳艳.自适应迭代傅里叶算法用于阵列方向图综合［J］.西安电子科技大学学报，2013，40(4):85-89.Wang Xinkuan，Jiao Yongchang，Tan Yanyan.Adaptive iterative Fourier algorithm for array pattern synthesis［J］.Journal of Xi′an Electronic and Science University，2013，40(4):85-89.(in Chinese)

［4］ 王卓，王杰.非均匀线阵天线阵因子综合方法的研究［J］.现代防御技术，2011，39(4):105-111.Wang Zhuo，Wang Jie.Methods for pattern synthesis of asymmetrical linear antenna arrays［J］.Modern Defense Technology，2011，39(4):105-111.(in Chinese)

［5］ Chen K，He Z，Han C.A modified real GA for the sparse linear array synthesis with multiple constraints［J］.Antennas and Propagation，IEEE Transactions，2006，54(7):2169-2173.

［6］ 王维博，冯全源.粒子群算法在阵列天线方向图综合中的应用［J］.西安电子科技大学学报，2011，38(3):175-180.Wang Weibo，Feng Quanyuan.Application of PSO algorithm in pattern synthesisfor antenna arrays［J］.Journal of Xi′an Electronic and Science University，2011，38(3):175-180.(in Chinese)

［7］ Ismail T H，Hamici Z M.Array pattern synthesis using digital phase control by quantized particle swarm optimization［J］.Antennas and Propagation，IEEE Transac-tions，2010，58(6):2142-2145.

［8］ 田雨波，朱人杰，李正强.粒子群优化算法中粒子更新方法研究［J］.江苏科技大学学报:自然科学版，2009，22(5):67-72.Tian Yubo，Zhu Renjie，Li Zhengqiang.Research on updating algorithms in particle swarm optimization［J］.Journal of Jiangsu University of Science and Technology:Natural Science Edition，2009，22(5):67-72.(in Chinese)

［9］ Taguchi G，Phadke M S.Quality engineering through design optimization［M］.New York，US:Springer，1989:77-96.

［10］ Hwang C C，Chang C M，Liu C T.A fuzzy-based Taguchi method for multiobjective design of PM motors［J］.IEEE Transactions on Magnetics，2013，49(5):2153-2156.

［11］ Chan K Y，Dillon T S.On-road sensor configuration design for traffic flow prediction using fuzzy neural networks and taguchi method［J］.Instrumentation and Measurement，IEEE Transactions，2013，62(1):50-59.

［12］ Chan K Y，Khadem S，Dillon T S，et al.Selection of significant on-road sensor data for short-term traffic flow forecasting using the taguchi method［J］.Industrial Informatics，IEEE Transactions，2012，8(2):255-266.

［13］ 张青洪，廖成，常雷，等.基于田口算法的超宽带TEM喇叭天线及阵列的优化［J］.科学技术与工程，2012，11(34):8481-8485.Zhang Qinghong，Liao Chen，Chang Lei，et al.Optimization of ultra-wide band TEM horn antenna and antenna arrays based on Taguchi′s method［J］.Science Technology and Engineering，2012，11(34):8481-8485.(in Chinese)

［14］ 聂利颖，张志鸿.一种基于田口-遗传算法确定的神经网络及其应用［J］.计算机应用与软件，2009，26(4):217-219.Nie Liying，Zhang Zhihong.The neural network based on Taguchi-genetic algorithm and its application［J］.Computer Applications and Software，2009，26(4):217-219.(in Chinese)

［15］ 田雨波，钱鉴.计算智能与计算电磁学［M］.北京:科学出版社，2008.