基于MOPSO算法的小型化复合结构槽螺旋天线设计

刘 东，王兆尹，田雨波，楼 群

(江苏科技大学电子信息学院，江苏镇江212003)

无线通信技术的快速发展和应用，推动了通信设备向小型化多用途的方向发展，而天线往往是制约无线通信系统小型化发展的主要障碍［1］，因此需要设计出一种小型、宽带、高效的天线.平面螺旋天线是一种宽频带天线［2］，因其具有结构紧凑、重量轻、输入阻抗稳定、相位中心固定、辐射圆极化波等特点，在诸多领域有着重要的应用.目前的平面螺旋天线主要有阿基米德螺旋天线和等角螺旋天线两种.因为平面螺旋天线是一种非频变天线［3］，而非频变天线大部分的辐射来自天线线宽为半个波长或周长为一个波长的区域，这就导致了当工作频率变小时，有效辐射区就自动移动到尺寸更大的地方，从而导致天线的整体尺寸变大.所以，在工作频率不变的情况下，如何对平面螺旋天线实施小型化设计已经成为该领域研究的一个热点与难点.

目前，现有的平面螺旋天线小型化方法主要有以下两种:①在末端采用曲折臂方法，通过延长电长度的方法达到小型化的目的，文献［4］即采用的这种方法，该设计的平面螺旋天线直径为128 mm，在0.8～4.0 GHz频段内的回波损耗小于－10 dB;②采用复合结构的形式用来减小天线的口径，文献［5］即采用此方法，并且在天线低频段加载了跨接电阻，该复合结构平面螺旋天线直径为50 mm，在0.75～8 GHz频段内回波损耗小于－10 dB.然而这两种办法对天线口径的缩小效果一般，并且或多或少的都会影响到天线的轴比、增益等电性能.在这里天线轴比指的是极化波瞬时电场矢量的端点轨迹的长轴和短轴之比，它代表了圆极化的纯度，是圆极化天线各项指标中尤为重要的一项，是衡量整机对不同方向信号增益差异的重要指标.

文中采用了槽线辐射结构［6－7］，将平面等角螺旋天线和平面阿基米德螺旋天线相结合，并且在天线的低频辐射区加载了跨接电阻，在天线外圈设置了两圈铜环.天线的设计为多目标优化问题，传统方法是将多个目标函数通过加权的形式转换为单目标形式进行优化计算，但这种处理方式的缺点是通过加权的形式不可能使每个优化目标函数达到预期值.近年来许多天线的设计使用了多目标优化形式［8－10］.文中利用多目标粒子群算法(multi-cbjective particle swarm optimization，MOPSO)［11］对复合结构平面螺旋天线进行优化，设计过程中采用电磁仿真软件CST微波工作室和MOPSO算法结合的方案.

1 天线结构设计

文中复合结构是将阿基米德螺旋天线和等角螺旋天线进行结合.阿基米德螺旋天线的半径随角度的增加而均匀增加，其曲线方程为:

式中:r0为起始半径，a为螺旋增长率，θ为幅角.在螺旋的周长为一个波长时为天线的主要辐射区，主要辐射区会随着频率的变动而变动，但方向图基本不变，一般来说天线外圈周长至少需要有1.25倍的最低频率对应的波长.平面等角螺旋天线的曲线方程为:

当a减小时，螺旋臂曲率增加，电流的衰减就愈快.因为等角螺旋天线臂长大于一个波长时，才会出现非频变特性，所以要求天线的半径至少等于1/4倍的最低频率对应的波长.

阿基米德螺旋天线相比等角螺旋天线，其增长率较慢，所以高频和低频性能要优于等角螺旋天线，但也因为较慢的增长率，导致了天线臂较细和环绕长度较长，从而天线损耗增大，所以其效率相对于等角螺旋天线来说要低.文中结合两种天线的优点，在天线中心采用等角螺旋，在外圈采用多段阿基米德螺旋，经过复杂变形后，使天线具有了一个相对很小的尺寸.如若仅采用阿基米德螺旋，则由于槽宽较小(本例中的槽宽为0.45 mm)，天线的磁流衰减很慢，如果想衰减同样大小的磁流，则需要很大的尺寸，文中设计的阿基米德和等角螺旋相结合的方法很好的解决了这个问题(图1).设计出的复合槽螺旋天线结构如图1a)，该天线直径是50 mm，基板采用的厚度为0.8 mm、相对介电常数为2.2的Rogers RT/duroid 5880介质板，内圈等角螺旋增长率选取0.221，外圈阿基米德螺旋增长率选取1/3，采用CST公司的CST微波工作室软件进行仿真.

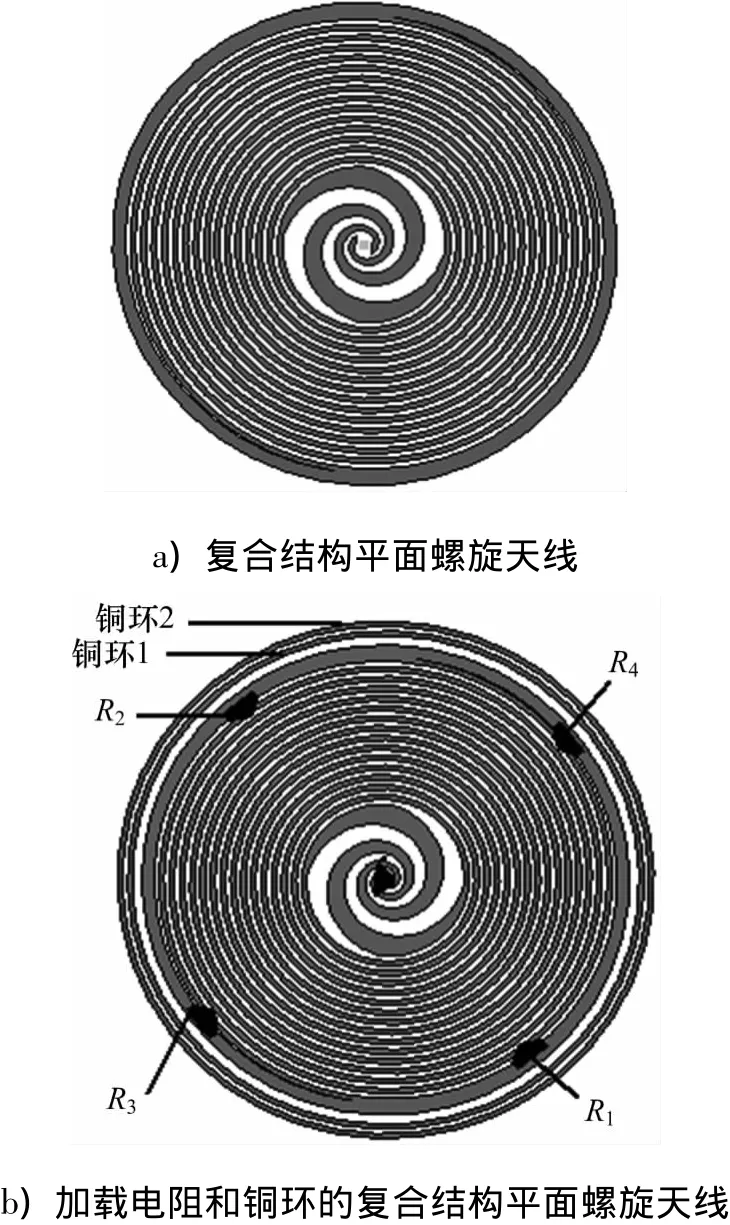
图1 平面螺旋天线Fig.1 Planar spiral antenna

图2为复合结构槽螺旋天线和经典阿基米德螺旋天线的回波损耗对比图和轴向轴比对比图.由图可以看出:相同尺寸下的普通阿基米德天线仅在3.1～8.3GHz频段内回波损耗小于－10dB，在4.2～18 GHz频段内轴比小于3 dB;而文中设计的复合结构槽螺旋天线，在1.9～18 GHz频段内回波损耗均小于－10dB，在2.2～18GHz频段内轴比小于3 dB.结论表明:在相同的尺寸下，文中设计的复合结构槽螺旋天线工作带宽更大，效果更好.

为了增大轴比带宽，实现低轴比特性，降低天线的回波损耗，以达到天线低频工作频率下移的目的，在上述设计的复合结构槽螺旋的基础上，在低频段使用跨接加载的方法，加载了4个贴片电阻并且在天线的外围加载了2个金属贴片圆环.加载圆环的目的，一是为了更加改善天线末端电流的截断效应，二是为了实现良好的圆极化特性.本例中给出的电阻阻值R1，R2均为 160 Ω，R3，R4均为 200 Ω;铜环1的宽度为0.5 mm，距离天线距离为 1 mm，铜环2宽度为0.5 mm，距离铜环1的距离为0.5 mm.加载贴片电阻和金属贴片铜环的复合结构槽螺旋平面天线见图1b).

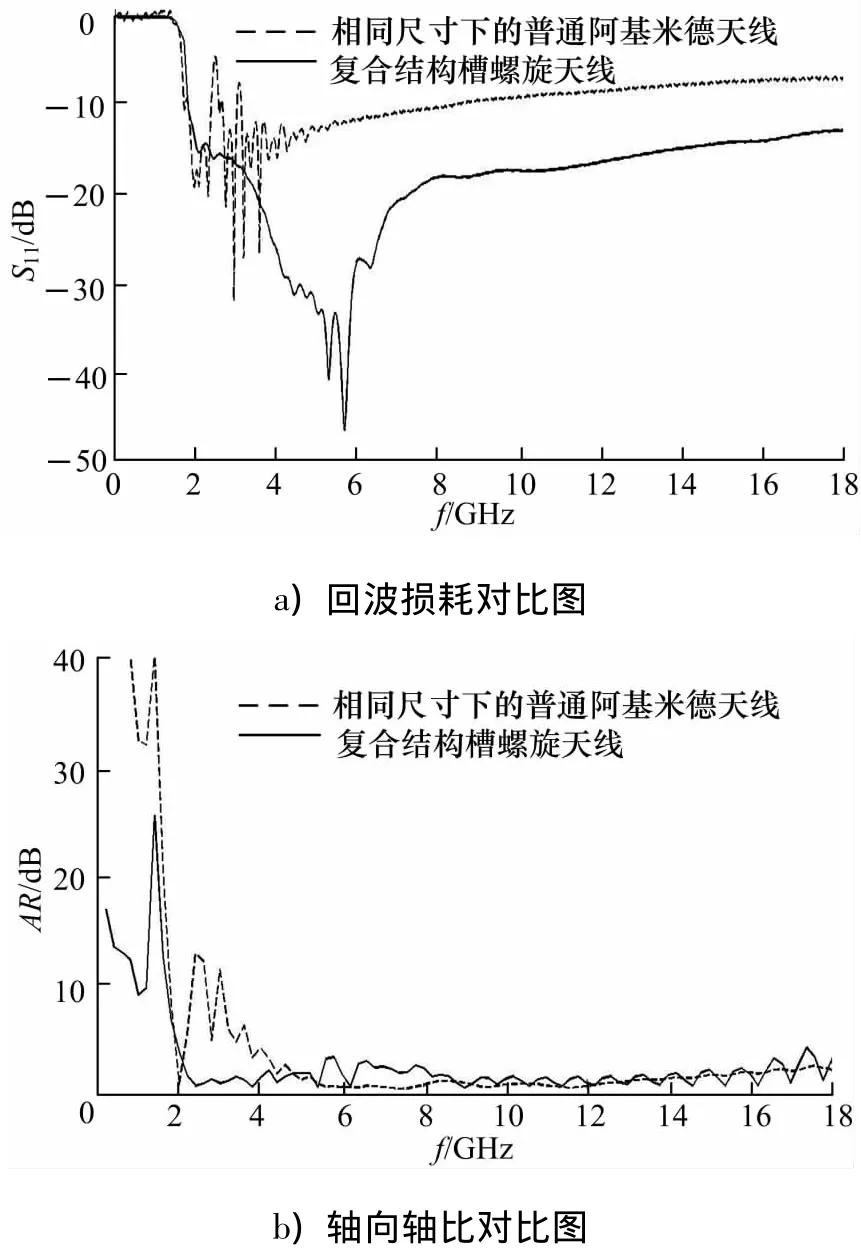
图2 复合结构天线和经典阿基米德天线主要性能对比图Fig.2 Composite structure antenna and classical Archimedes antennaper for mance comparison chart

图3为加载贴片电阻以及金属贴片铜环的复合结构槽螺旋天线和未加载的复合结构槽螺旋天线的回波损耗以及轴向轴比的对比图.由图可以看出:加载了电阻和铜环以后，天线的低频段由1.9 GHz下移到1.6 GHz，并且在大部分频段内，回波损耗也有所下降;天线的轴比性能变化更为明显，由2.2～18 GHz频段内轴比小于3 dB，变为1.4～18 GHz频段内轴比小于3 dB，结果表明:增加了电阻和铜环以后，天线的性能总体上得到了提高.

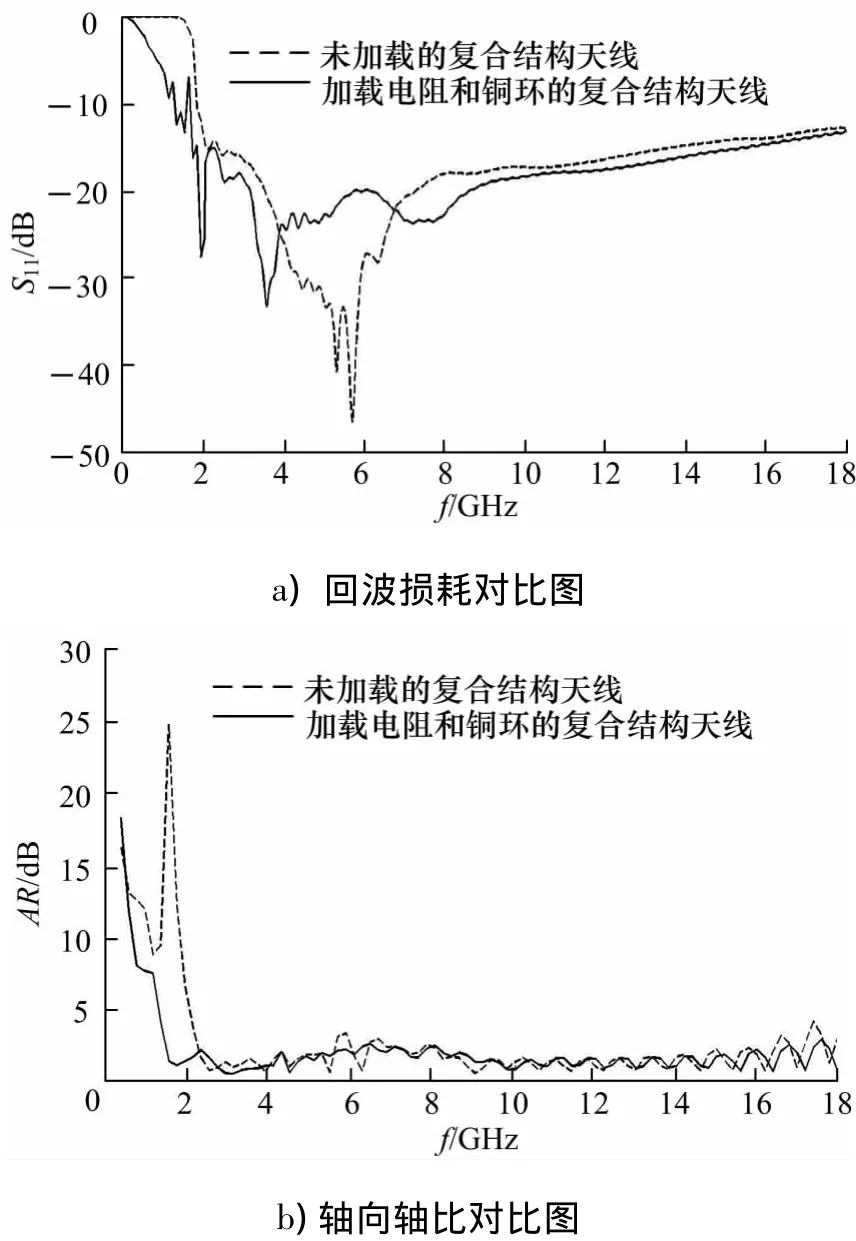
图3 加载电阻和铜环前后的复合结构天线性能对比图Fig.3 Performance comparison of composite structure diagram antenna loading resistance before and after copper ring

2 天线优化设计

决定天线性能的指标有多个，如:回波损耗、轴比、增益等，这就使得天线的设计为一多目标优化计算问题，文中采用多目标粒子群算法进行优化设计［12］，迭代规则可简单表示为:

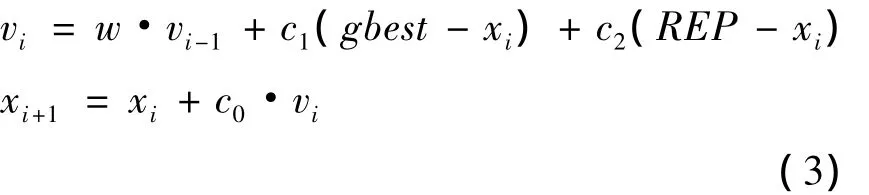
式中:vi为粒子当前速度，vi-1为粒子上一代的速度;w为惯性权重;gbest为粒子最佳位置;xi为粒子当前位置;xi+1为粒子下一代达到位置;c0，c1，c2为学习因子;REP为根据轮盘选择方式［13］选择出的分布较紧密的帕累托最优解集中的解.REP，ω，c0，c1，c2的取值以及算法具体流程采用文献［14］提出的使用MOPSO与CST协同仿真的方法.优化目标为改善天线的回波损耗以及轴比.由于平面螺旋天线的对称性，电阻1和电阻2对称，电阻3和电阻4对称，故设优化参数电阻1，电阻2阻值大小为RA，电阻3和电阻4的大小为RB，铜环1的内外半径为r1和r2，铜环2的内外半径为r3和r4，在优化过程中需要合理调节这6个参数.

在优化设计中，选取适应度函数为:

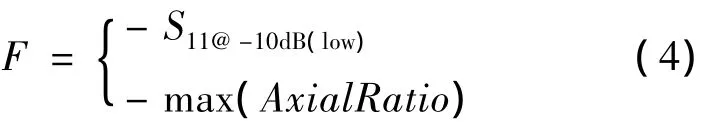
式中:-S11@-10dB(low)为回波损耗小于10 dB时的低频，-max(AxialRatio)为轴为最大处的频率.在优化计算过程中取粒子数为20，迭代次数为100，共需计算20×100=2000次，由于本次实验所用设备配置较低等原因，利用CST仿真一次大约需要45 min，所以完成2000次优化过程大约需要1500h.考虑到工作量巨大，在这里利用Matlab并行计算工具箱［15］，将CST的仿真计算分配到不同的10台计算机，完成分布式协同仿真优化，分布式计算逻辑框图如图4.使用10台同样配置的电脑来完成分布式计算，这10台电脑为分布式计算中的服务端.此外，另选1台电脑作为客户端和管理端，将原本1台计算机完成的任务通过管理端调度分配到10台计算机分布计算，这样计算时间大约可以减少为原来的1/10，优化设计耗时将大大减少.本次仿真优化计算历时约一周，优化计算，得出的6个参数值如表1.

图4 分布式计算逻辑框图Fig.4 Distributed computing logic diagram

表1 优化结果Table 1 Results of optimization

图5分别为优化前、后天线的回波损耗以及轴向轴比对比图，由图可以得出:天线的低频段由1.6GHz下移到1.1 GHz，并且在大部分段内，回波损耗也有所下降;天线的轴比性能变化更为明显，由1.4～18 GHz频段内轴比小于3 dB，变为0.8～18 GHz频段内轴比小于3 dB.图6给出了几个重要频点的XOZ面方向图.上述结果表明，使用多目标粒子群算法对天线进行优化后，天线的性能得到提高.

图5 优化前后的天线主要性能对比Fig.5 Antenna main performance comparison of before and after optimization

图6 几个主要频点的XOZ面方向图Fig.6 XOZ plane of several main frequency diagram

3 结论

文中设计了一个复合结构槽螺旋天线，该天线具有良好的宽频带特性、圆极化特性，并且天线的直径仅为54mm，较普通的平面螺旋天线相比，口径得到大幅相减的同时，电性能得到了优化，达到了小型化设计的目的.使用多目标粒子群优化算法，利用Matlab软件实现了分布式协同优化仿真，使天线的低端工作频率下移，并且轴比得到了优化.此设计方法，也为其他类型的天线优化提供了一种方案.

References)

［1］ Takatori Y，Kagoshima K.Miniaturization of base station antennas by using adaptive antenna technique for indoor high-speed wireless communication systems［C］∥IEEE Conference Publications.USA:IEEE，1998:480－484.

［2］ Taylor T D.Introduction to ultra-wide band radar system［M］.Boca Raton:CRC Press，1995:13－18.

［3］ Rumsey V H.Frequency independent antennas［R］.［S.l.］:IRE National Convention Record，1957:114－118.

［4］ 宋朝晖，李红梅，杨汉英，等.曲折臂形式的阿基米德天线小型化探究［J］.微波学报，2009，25(2):53－37.Song Zhaohui，Li Hongmei，Yang Hanying，et al.Study on a miniaturized meander archimedean spiral antenna［J］.Journal of Microwaves，2009，25(2):53 － 37.(in Chinese)

［5］ 朱玉晓，钟顺时，许赛卿.小型化超宽带槽螺旋天线设计［J］.微波学报，2009，5(1):39－41.Zhu Yuxia，Zhong Shunshi，Xu Saiqing，et al.Design of miniaturized super-broadband slot spiralantenna［J］.Journal of Microwaves，2009，5(1):39 －41.(in Chinese)

［6］ 高向军，王光明，朱莉，等.一种新型宽带微带缝隙天线的设计［J］.电子科技大学学报，2007，36(5):883－885.Gao Xiangjun，Wang Guangming，Zhu Li，et al.A new method to design a wide band microstrip slot antenna［J］.Journal of University of Electronic Science and Technology of China，2007，36(5):883 － 885.(in Chinese)

［7］ Sze Jiayi，Wong Kinlu.Bandwidth enhancement of a microstrip-line-fed printed wide-slot antenna［J］.IEEE Transactions onAntennasandPropagation，2001，(7):1020－1023.

［8］ Yuan X，Li Z，Rodrigo D，et al.A parasitic layerbased reconfigurable antenna design by multi-objective optimization［J］.IEEE Transactions on Antennas and Propagation，2012，60(6):2690－2701.

［9］ Goudos S，Gotsis K，Siakavara K，et al.A multi-objective approach to subarrayed linear antenna arrays design based on memetic differential evolution［J］.IEEE Transactions on Antennas and Propagation，2013，61(6):3042－3052.

［10］ Couckuyt，Deschrijver，Dhaene.Towards efficient multiobjective optimization:multiobjective statistical criterions［C］∥IEEE Congress on Evolutionary Computation(CEC).USA:IEEE，2012:1 －8.

［11］ Coello C A.MOPSO:A proposal for multiple objective particle swarm optimization［C］∥Proceedings of the2002Congress on Evolutionary Computation(CEC′02).Honolulu，HI:IEEE，2002:1051 －1056.

［12］ Coello C A，Pulido G T，Lechuga M S.Handling multiple objectives with particle swarm optimization ［J］.IEEE Transaction on Evolutionary Computation，2004，8(3):256－279.

［13］ 纪震，廖惠连.粒子群优化算法［M］.北京:科学出版社，2009:35－38.

［14］ Nabo J，Yahya R S.Parallel particle swarm optimization and finite-difference time-domain(PSO/FDTD)algorithm for multiband and wide-band patch antenna designs［J］.IEEE Transactions on Antennas and Propagation，2005，53(11):3459 －3468.

［15］ Goryawala G，Guillen M.A comparative study on the performance of the parallel and distributing computing operation in MatLab［C］∥2010 24th IEEE International Conference on Advanced Information Networking and Applications.USA:IEEE，2010:150 －157.