Mecanum轮全方位移动小车嵌入式控制系统的设计

唐 炜，刘 勇，于香志，胡海秀，刘伟昌

(江苏科技大学机械工程学院，江苏镇江212003)

全方位移动机构具有平面内完全的3个运动自由度，即沿X，Y轴方向的移动和绕Z轴的转动.Mecanum轮结构紧凑、运动灵活，能稳定地实现全方位移动.目前，以Mecanum轮为代表的轮式全方位移动机构的研究已成为一大热点.与传统的轮式移动机构相比，Mecanum轮全方位移动机构可实现原地侧移、零转弯半径旋转等运动，其空间利用率高，在狭窄操作环境或者需要频繁转向的场合中具有独特的运动灵活性，尤其在仓储运输、生活服务等领域具有广阔的应用前景［1－4］.

目前，国内已有部分学者对Mecanum轮做了相关的研究.文献［1］中研究了模糊滑模轨迹跟踪控制算法在Mecanum轮全方位移动平台的应用;文献［2］中讨论了Mecanum轮全方位运动系统的约束条件及奇异位形;文献［3］中研究了采用API进行Mecanum参数化建模的方法;文献［4］中介绍了Mecanum轮的原理结构并进行了基于ADAMS软件的运动仿真.但上述研究主要侧重于全向运动分析和控制算法仿真研究，未更多涉及Mecanum轮技术的工程化应用，尤其缺少理论分析与样机实测的对比验证.文中在对Mecanum轮机器人小车进行运动学分析的基础上，重点设计了基于STM32微控制器的嵌入式控制系统，并采用在线模糊自整定PID算法以保证控制的实时性和精度，最后借助于测距传感器对Mecanum轮全方位移动机器人样机的实际运动性能进行了测试分析，以期掌握全方位移动机器人研究的关键技术，为下一步的工程化推广应用打下坚实基础.

1 Mecanum轮结构

Mecanum轮在1973年由瑞士工程师Bengt Ilon首先设计提出，其结构特点是沿着轮子轮毂周围排列着与轮子成一定偏置角度的辊子，辊子可将轮子旋转的部分力转换到轮子旋转的法线方向，通过各轮子间转速和转向的配合，以合成任意方向的力矩，从而驱动小车往任意方向进行移动.设计使用了两端支撑形式的Mecanum轮，其外形如图1a)，其中m为轮毂的回转轴线，n为辊子的轴线.辊子可绕自身轴线旋转，所有的辊子外廓近似包络成圆柱形，如图1b).轮子与地面接触的任意时刻，至少有一个辊子与地面发生接触，从而避免运动过程中的振动，确保辊子与地面接触的连续性和小车运动的平稳性.通常，每个辊子外围包罗一层橡胶缓冲材料以减少辊子的磨损和运动噪音，并在一定程度上降低对Mecanum轮的安装要求.

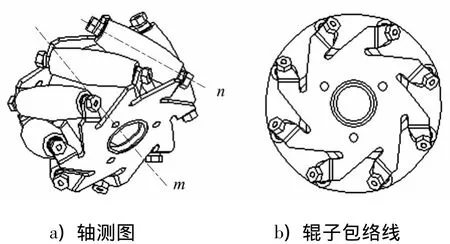
图1 Mecanum轮外观Fig.1 Appearance of Mecanum wheel

文献［5］中分析推导出的以角度α为变量的辊子轮廓曲线参数方程如下:

式中:d为轮毂轴线m和辊子轴线n的公垂线长度;δ为辊子轴线的偏置角度;r为辊子包络圆柱体底面半径;x*(α)为辊子轴向距离;z*(α)为辊子半径.根据式(1)所绘制的辊子实体轮廓如图2.

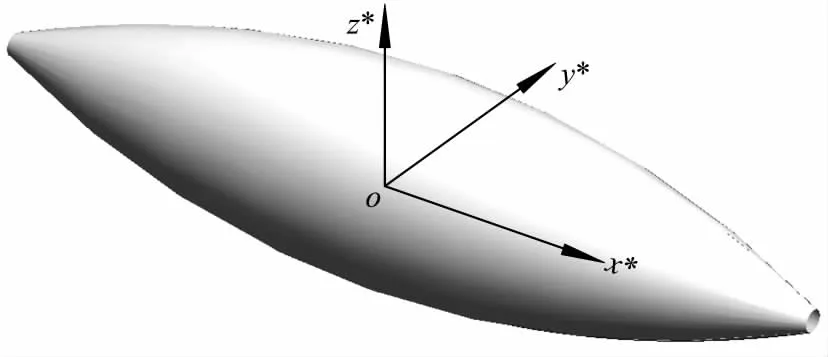
图2 辊子实体外形Fig.2 Appearance of the roller

2 全方位移动机构运动分析

Mecanum轮组布局参考了文献［6］中关于轮组结构形式的研究.图3为四轮驱动的全方位移动小车俯视图，实际与地面接触的辊子偏置方向与图示相反，轮毂的轴线均与y轴平行，四轮的中心恰好呈现为长方形的4个顶点;对角线上2个Mecanum轮上的辊子具有相同的旋向，各辊子偏置角相等.

图3 四轮布局俯视图Fig.3 Top view of four-wheel layout

为简化运动学建模，对小车运动过程做以下假设:小车车体为刚体，忽略变形;车体运动在平坦地面上，忽略地面不平而带来的问题;轮子与地面间的接触为纯滚动，没有相对滑动.

小车运动学模型建立的基本思想为:先从Mecanum单轮出发写出着地辊子到Mecanum轮中心点Oi的速度表达式，然后从整个移动小车出发分析平台质心c点到Mecanum轮中心点速度的表达式，从而联立这两个表达式并化简可得到Mecanum四轮与小车中心速度映射关系方程式即运动学模型.在此，定义Mecanum轮转角为θ，辊子转角为ρ，中心点为Ri，小车四轮着地点连线间的长、宽的一半为L、W，Mecanum轮半径为R，辊子最大半径为Rroller，偏置角定义为δ，单位向量fi过点Oi且垂直于轮子轴线及线段OiRi，单位向量hi过点Oi且垂直于辊子轴线及线段OiRi.用向量(vx，vy，ωz)为全方位机器人小车中心点的广义速度，用向量(ω1，ω2，ω3，ω4)为4个轮子的转动角速度.对于单个轮子的速度，能得到表达式:

对于以C点为中心在平面上运动的Mecanum多轮移动小车，其运动学方程为:

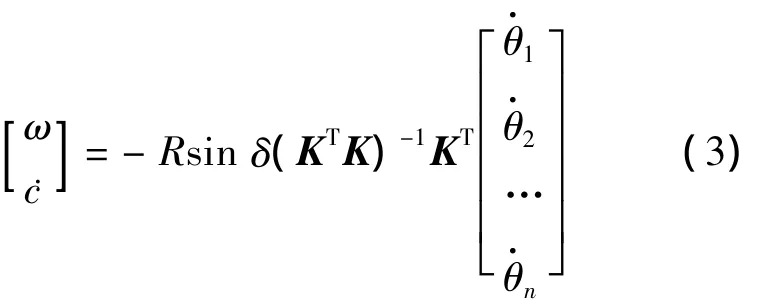
式中:K为n×3的矩阵.根据文中设计的四轮布局形式，最终建立的全方位移动平台逆运动学模型如下式:

可以看出，一旦设定了全方位移动小车在平面内的运动规律(vx，vy，ωz)，则可由式(4)所示的逆运动学模型解算出4个轮子的转速和转向，从而实现该小车在平面内的全方位移动［7］.

3 控制系统总体结构

文中控制系统选用高性能、低成本、低功耗微控制器芯片STM32F103ZE.它具有ARM Cortex－M3内核，72MHz的最高主频，1.25DMips/MHz的指令执行速度，并集成有丰富的内设资源和多种外设接口，能较好满足本系统多路直流电机控制信号的输出及其转速实时反馈的要求.

系统总体结构如图4.上位PC机与小车主控制器之间通过蓝牙方式进行无线通信.系统运行时，首先由PC机将包含有小车运动规律的控制参数以报文的形式发给小车主控制器，待后者接收成功后立即提取小车广义速度参数，并按式(2)转换成为四车轮的转动角速度(含转向)，然后再由主控制器同时向各电机驱动模块发出转速对应的PWM控制信号.在直流电机转动的同时，其尾部安装的光电编码器能将实时速度反馈给主控制器用于转速调节，从而形成反馈控制［8］.另外，测距传感器能实时测量小车与周围物体的距离，可用于避障、速度实测或通过测距的方法来评价小车的运动性能.

在此，车轮驱动用电机选用了德国Faulhaber直流空心杯电机，它具有突出的节能特性、灵敏方便的控制特性和稳定的运行特性.测距传感器选用超声波传感器，安装在车身对应的x和y方向上，其可探测范围为2～450cm，精度为±3mm.

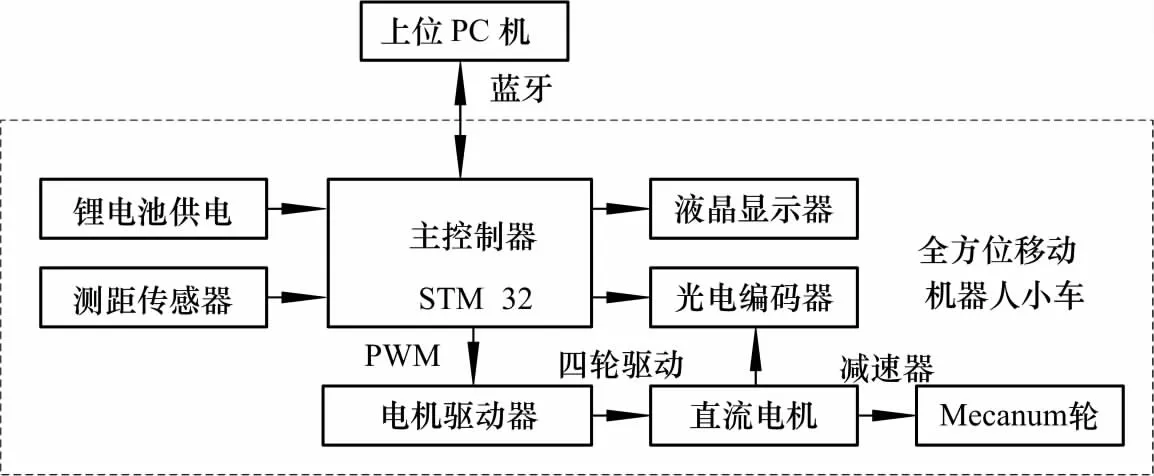
图4 控制系统基本组成Fig.4 Basic components of the control system

4 模糊自整定PID控制算法

实际系统运行时，辊子与路面的接触情况会受到路面实际状况的影响，而不利于保证小车控制的精度.路面变化会对小车的控制精度产生较大影响，同时，直流电机的数学模型也难以精确描述.常规PID算法的控制效果主要依赖于固定的Kp，Ki，Kd3个参数，而对于大扰动、非线性系统往往不能达到较好的自适应性和鲁棒性［9］.文中采用了模糊自整定PID控制算法，在小车运行时对上述参数进行在线自适应调整，从而使系统具有更好的鲁棒性和控制精度.

4.1 模糊控制器原理

模糊自整定PID控制器的基本结构如图5.控制系统在不同偏差e和偏差变化率ec输入的情况下，通过模糊控制器可以在线对PID参数Kp、Ki、Kd进行动态调整.模糊控制的工作流程主要分3个部分:模糊化、模糊推理、清晰化［10］.

图5 模糊自整定PID控制器原理Fig.5 Layout of fuzzy self-turning PID controller

4.2 参数模糊化

模糊化的作用是将输入的精确量变换到要求的论域范围.本控制器输入的是误差量e=r－y及误差变化率ec=de/dt.e和ec的论域为{－3，2，－1，0，1，2，3}，对应的模糊集合是{NB，NM，NS，ZO，PS，PM，PB}，其含义分别是:负大、负中、负小、零、正小、正中、正大.为了简化主控制器算法，提高控制实时性，在此选用三角形隶属度函数，如图6，任意输入对于模糊集合的隶属度均不小于0.5.

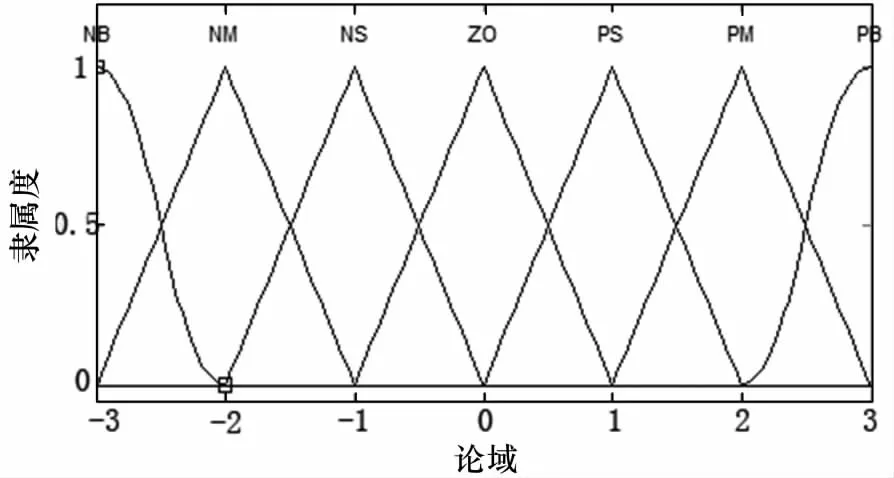
图6 e，ec的隶属度函数Fig.6 Membership function for the e ＆ ec

4.3 模糊推理

模糊推理是模糊控制器的核心，该过程是基于推理规则进行的.推理规则包括了用语言变量表示的一系列控制规则，它反映了专家的经验和知识，通常采用如下形式描述:

if(满足一组条件)then(推出一组结果)

例如，本系统的某条模糊条件句为:if(E is NB)and(EC is NB)then(Kpp is PB)(Kii is NB)(Kdd is PS)，它表示:如果误差是负大且误差变化率是负大，那么输出的3个参数的调整值分别应是正大、负大和正小.

在进行模糊推理之前，首先要定义ΔKp，ΔKi和ΔKd3个参数的模糊论域.本系统模糊论域为:

ΔKp={－ 0.18，－ 0.12，－ 0.06，0，0.06，0.12，0.18};

ΔKi={－0.0458，－0.0305，－0.0153，0，0.0153，0.0305，0.0458};

ΔKd={－0.0338，－0.0225，－0.0113，0，0.0113，0.0225，0.0338}.

根据专家经验，在不同e和ec下，被控过程对参数Kp、Ki和Kd的自整定要求须对应各自模糊规则表.表1～3分别为Kp，Ki，Kd的模糊推理规则表.

表1 Kp模糊推理规则Table 1 Fuzzy reasoning rules for Kp

表2 Ki模糊推理规则Table 2 Fuzzy reasoning rules for Ki

表3 Kd模糊推理规则Table 3 Fuzzy reasoning rules for Kd

4.4 清晰化计算

通过模糊推理得到的是模糊量，而实际的控制参数是清晰值.清晰化计算的目的就是将模糊量转换为清晰量，具体方法有最大隶属度法、中位数法和重心法等.文中选用了重心法［11］，它取隶属度的加权值为清晰值，对于离散的论域有:

式中:Z0为清晰值;Zi为隶属度值;uc(zi)为模糊变量.求得清晰值后，还要经过尺度变换才能得到实际的控制量ΔKp，ΔKi和ΔKd.在此采用线性变换，即当ΔKp论域为［Z1，Z2］，ΔKp实际变化范围为［U1，U2］，则ΔKp的实际调整值应为:

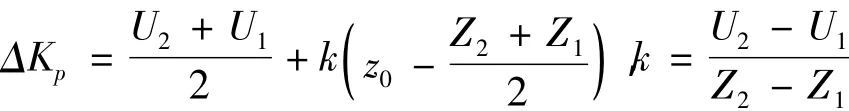
式中:k为尺度变换的比例因子.

5 控制系统软件设计

5.1 上位机

上位PC 机运行的控制程序是在VB.NET环境下设计的，其主要功能是将PC机所设定的全方位机器人小车运动速度(vx，vy，ωz)等参数通过蓝牙无线方式发送给小车主控制器，同时也在PC机上显示小车的实时工作状态和运行轨迹.图7为部分操作界面.其中，图7a)为手动输入小车运动参数;图7b)为较为形象的图形操作界面，但运行速度在程序中是固定的，主要用于系统调试.

图7 上位机软件控制界面Fig.7 Control interface of the host computer

5.2 主控制器

小车控制器主程序流程如图8a)，其中，主程序首先对液晶屏、蓝牙收发、外部中断等功能模块进行初始化，然后再检查串口状态标志判断是否成功接收到上位机的控制指令.如果接收成功，则根据事先约定的通信协议提取出小车运动控制参数，并根据小车运动学模型计算出4个Mecanum轮转速的设定值.图8b)利用串口中断对上位机发来的控制指令进行识别确认，而图8c)利用定时器中断来实现采样时间T，并获得4个车轮的实际转速，更新模糊自整定PID控制算法所需的输入参数e和ec，并完成对小车的反馈控制.

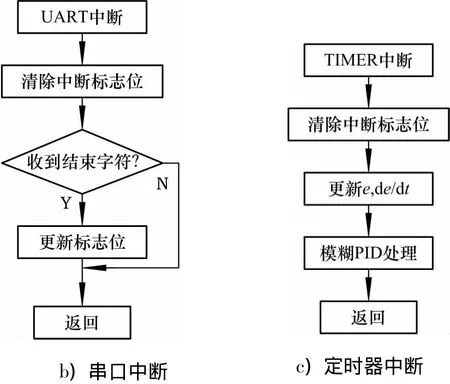
图8 主控制器程序流程Fig.8 Program flow chart of the micro-controller

6 实验分析

图9为实验用Mecanum轮全方位移动小车样机.为了验证本控制系统的可行性，并测试模糊自整定PID控制算法的实时性及其控制精度，在此主要从小车运行稳定性、重复性等方面进行综合评价.

图9 全方位移动小车实验样机Fig.9 Phototype of the omni-directional movement vehicle

6.1 实验方法

样机运动实验在由长方形空间内进行，通过使用车身上横向和纵向安装的超声波测距传感器实时检测小车相对于两方向的垂直距离，从而完成相关性能参数的评价.

利用STM32微控制器片内的DAC模块将各电机的实时转速n反馈转换为能被数字示波器捕获的电压信号输出，即可获得电机控制的动态响应特性曲线，以便观察不同控制算法下的实际控制效果.

6.2 控制算法比较

在此，对比了在相同阶跃输入下常规PID和模糊自整定PID两种控制算法的动态响应过程，如图10.其中，曲线1，2分别是系统在模糊自整定PID、常规PID算法下的阶跃响应曲线.经过多次整定后，两种算法下的超调量几乎都为零，而曲线1的上升时间t为0.21s，相对于曲线2的0.35 s有明显缩短，反映出模糊自整定PID控制算法可有效提高控制系统响应的快速性.这也有利于在路面不平时，通过系统的快速响应而提高小车行驶轨迹的准确性.

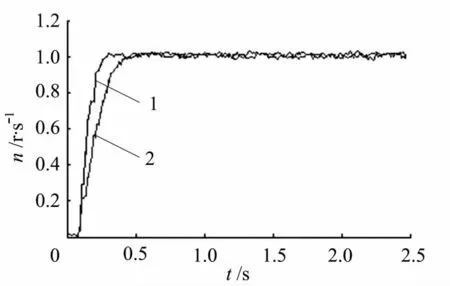
图10 系统动态响应特性Fig.10 Dynamic response performance

6.3 小车运动实验

在实验室条件下，对小车样机进行了前后直线运动、横向侧移运动、斜45°直线运动和多矩形轨迹运动等多组实验，以对其运动性能进行评估.

图11为样机在设定速度20cm/s(曲线1)和10 cm/s(曲线2)条件下实测前向距离d与时间t之间的关系.理论上，此时前向距离与时间呈严格线性关系，即图中虚线是以车身初始位置为起始点的一条直线.可以看出:理论设定速度与实际行使速度吻合度较高，小车的前向行驶总体平稳.图12为样机在横向侧移时前向距离的波动曲线.理论上，此时样机纵向位移应为零，故图中虚线的纵坐标恒定不变.理论值初始距离为18.27cm，因受地面不平度的影响，存在少许“敲地”现象，导致前向波动最大偏移量约为1cm.这符合场地实际情况.图13为样机斜向45°直线运动，其实际运动轨迹和理论轨迹基本重合，小车行驶平稳.

为了测试多次行驶轨迹的重复性误差，样机进行了连续矩形轨迹运动实验，如图14.其中，曲线1～3为连续3次小车的实际运行轨迹.可以看出，由于车身自身惯性的存在，在换向瞬间小车会产生少量横向dx或纵向偏移dy以及绕自身轴线的小角度旋转.图中A处主要存在少许转向漂移，而B处反映出横向侧移时运动方向上存在微量偏差.

图11 直线运动Fig.11 Straight line movement

图12 横向侧移运动Fig.12 Lateral movement

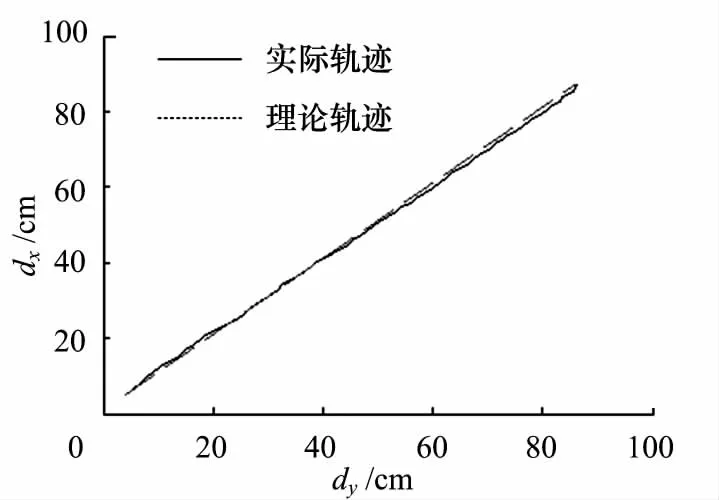
图13 斜45°直线运动Fig.13 Straight line movement in 45°

图14 连续矩形运动Fig.14 Continuous rectangular movement paths

6.4 实验分析

通过以上实验，总体说明了运动学模型的准确性、控制系统硬件设计的合理性以及模糊自整定PID控制算法具有良好的控制效果，验证了小车在平面内具有良好的全方位移动性能.

需要说明的是，由于传感器自身存在误差，Mecanum轮加工及样机安装也不可避免存在误差，同时因实验条件的限制，导致前文在建立小车运动学模型时所作的假设无法全面保证，同时小车的重心也不可能恰好与其几何中心完全重合.以上因素都会影响小车实际的运动平稳性及其控制精度，如横向运动时产生抖动、小车运动方向突然改变时因车身惯性引起的微量滑动等.

7 结论

在描述Mecanum轮结构的基础上，分析了四轮全方位移动小车的运动学模型，并完成了控制系统软硬件设计，并采用蓝牙无线通信、液晶屏实时状态显示等手段增强了小车的人机交互性，便于观察和调试.研究了模糊自整定PID控制算法及其在嵌入式控制器中的实现，兼顾了算法的运算量和微控制器的处理性能，保证了控制的实时性，实测效果良好.总体上看，Mecanum轮全方位移动小车结构紧凑、运动灵活，能稳定地实现全方位移动，具有原地侧移、零回转半径等独特优点，空间利用率高，应用前景广阔.

References)

［1］ 王双双，张豫南，王和源，等.全方位移动平台模糊滑模轨迹跟踪控制［J］.微特电机，2012，40(8):63－66.Wang Shuangshuang，Zhang Yunan，Wang Heyuan，et al.Trajectory tracking based on fuzzy sliding mode control for omnidirectional platform［J］.Drive and Control，2012，40(8):63 －66.(in Chinese)

［2］ 王一治，常德功.Mecanum轮全方位运动系统的约束条件及奇异位形［J］.上海大学学报:自然科学版，2009，15(2):181 －185.Wang Yizhi，Chang Gegong.Motion restricted condition and singular configuration for mecanum wheeled omnidirectional motion system［J］.Journal of Shanghai University:Natural Science，2009，15(2):181 － 185.(in Chinese)

［3］ 张豫南，田鹏，王双双，等.采用SolidWorks API的全方位轮参数化实体建模［J］.现代制造工程，2013(2):59－62.Zhang Yunan，Tian Peng，Wang Shuangshuang，et al.Parametric solid modeling of omnidirectionalwheel based on SolidWorks API［J］.Modern Manufacturing Engineering，2013(2):59 －62.(in Chinese)

［4］ 刘中新，张春亮，王占富，等.全方位移动平台运动分析与仿真［J］.机械与电子，2013(8):16－19.Liu Zhongxin，Zhang Chunliang，Wang Zhanfu，et al.Omnidirectional mobile platform motion analysis and simulation［J］.Machinery and Electronics，2013(8):16－19.(in Chinese)

［5］ Gfrerrer A.Geometry and kinematics of the Mecanum wheel［J］.Computer Aided Geometric Design，2008，25:784－791.

［6］ 王一治，常德功.Mecanum四轮全方位系统的运动性能分析及结构形式优选［J］.机械工程学报，2009，45(5):307 －310，316.Wang Yizhi，Chang Degong.Motion performance analysis and layout selection for motion system with four mecannum wheels［J］.Journal of Mechanical Engineering，2009，45(5):307 －310，316.(in Chinese)

［7］ 陈文科，陈志，王志，等.万向电动底盘控制系统设计［J］.农业机械学报，2013，44(6):19 －23，34.Chen Wenke，Chen Zhi，Wang Zhi，et al.Control system design of omnidirectional electric chassis［J］.Transactions of the Chinese Society for Agricultural Machinery，2013，44(6):19 －23，34.(in Chinese)

［8］ 王直，丁超.基于STM32的自动涂装机伺服控制系统［J］.江苏科技大学学报:自然科学版，2013，27(3):257－262.Wang Zhi，Ding Chao.Study of servo control for automatic painting machine based on STM32［J］.Journal of Jiangsu University of Science and Technology:Natural Science Edition，2013，27(3):257 －262.(in Chinese)

［9］ Tan Xiankun，Su Jingbo，Li Lei.Fuzzy optimization and learning based parameter auto-tuning method for PID controllor［J］.Hydromec-hatronics Engineering，2013(24):116－120.

［10］ 吴振顺，姚建均，岳东海.模糊自整定PID控制器的设计及其应用［J］.哈尔滨工业大学学报，2004，36(11):1578－1580.Wu Zhenshun，Yao Jianjun，Yue Donghai.A self-tuning fuzzy PID controler and its application［J］.Jounal of Harbin Institute of Technology，2004，36(11):1578 －1580.(in Chinese)

［11］ Karasakal O，Guzelkaya M，Eksin I.Online tuning of fuzzy PID controller via rule weighing based on normalized acceleration［J］.Engineering Applications of Artificial Intelligence，2013(26):184 －197.