幂律非牛顿流体在偏心圆环管中流动和传热的数值计算

张钧波，张 敏

(1.南京师范大学泰州学院，江苏泰州225300)

(2.南京理工大学能源与动力工程学院，江苏南京210094)

非牛顿流体在偏心圆环管中的流动和传热在石油化工、生物、机械、食品等领域中有着广泛的应用，但因非牛顿流体剪切应力与剪切速率的非线性关系，导致其数值计算比牛顿流体更加困难.近年来国内外学者对非牛顿流体在圆环管道中流动和传热或牛顿流体在偏心圆环中的流动和传热进行了很多研究［1－7］，但是对非牛顿流体在偏心圆环中的流动和传热考虑的却很少.文中在数值计算过程中采用基元中心法对非牛顿流体的非线性粘性系数进行离散，解决了幂律流体模型迭代收敛困难的问题，并在内壁恒温，外壁绝热的边界条件下，对非牛顿流体在偏心圆环管中充分发展层流的流动和传热进行数值计算.分析了偏心圆环管的偏心率和非牛顿流体的幂律因子对圆环通道内速度和温度分布的影响，具有实际的理论意义和工程应用价值.

1 控制方程和边界条件

1.1 流动控制方程和边界条件

偏心圆环管横截面如图1，图中ri和ro分别为内外圆半径，ε为偏心距，即内外圆圆心距.文中以偏心圆环管内充分发展层流为研究对象.

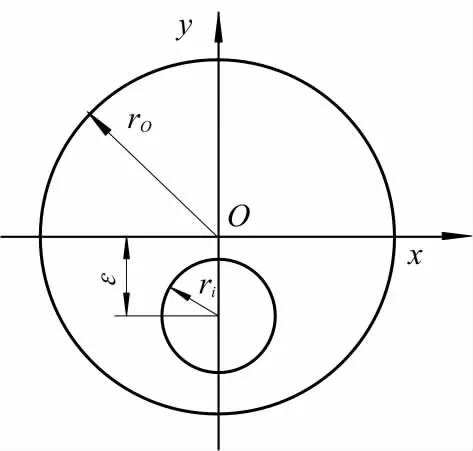
图1 计算区域几何图形Fig.1 Geometric drawing of computational domain

对于充分发展层流问题，沿圆环管轴向的流动控制方程为:

式中:w为流体轴向的流动速度;dp/dz为圆环管轴向的压力降;μ为流体动力粘度;考虑偏心圆环管横截面的对称性，取偏心圆环管横截面的右半部分为数值计算几何模型并生成网格，计算网格如图2.

图2 计算区域网格Fig.2 Grid of computation domain

边界条件为:

为简化计算和增加程序的通用性，将各计算参数无量纲化，取外圆半径ro为长度量纲，则无量纲坐标(x*，y*)为:

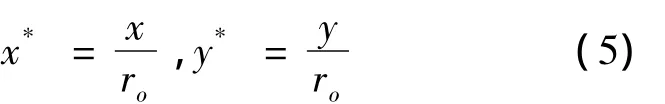
偏心率和半径比分别为:

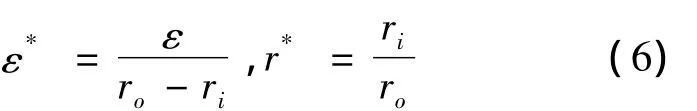
定义无量纲速度w*:

式中:K和n是流体的无量纲常数.将各参数的无量纲形式代入控制方程中:

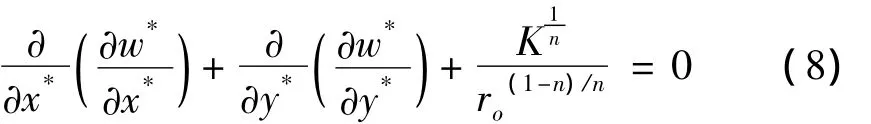
同样可得边界条件:

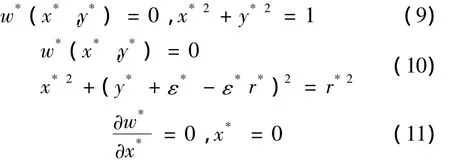
1.2 传热控制方程和边界条件

对于充分发展层流的稳态导热问题，温度只与流体的轴向速度有关，因此传热控制方程可表示为:

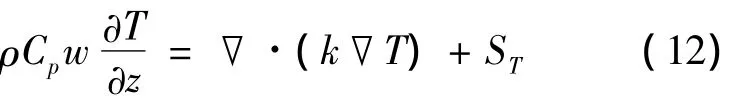
式中:ρ为密度;Cp为定压比热;k为热传导系数;ST为外热源或热汇为温度梯度.

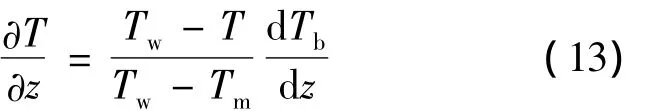
式中:Tw为壁面温度;Tb为平均体温度;Tm为平均温度.

假设无外热源，则控制方程(12)可简化为

取偏心圆环管的传热边界条件为内壁恒壁温外壁绝热，即

控制方程的无量纲式为:

wm为平均速度，无量纲坐标为:

Dh为水力直径，无量纲温度为:

2 数值计算方法

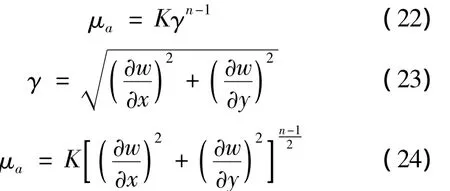
对于流动控制方程(8)和传热控制方程(19)的离散，采用二阶精度的有限体积法，与文献［8－9］的计算方法相同.以下重点介绍采用基元中心法对幂律非牛顿流体表观粘性系数的离散.粘性系数可用下式表示:式中:K是流体物性系数;n为幂律因子;γ为应变速度.对于充分发展层流，w为流体轴向流动速度，运用基元中心法对 ∂w/∂x和 ∂w/∂y进行离散，假设两控制体中心点连线上速度梯度呈线性变化关系，则此连线中点处的速度梯度值即为相邻控制体交界面处的速度梯度［10］.

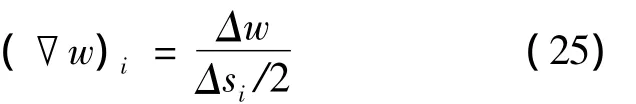
式中:i为相邻控制体编号

则速度梯度在x和y方向上的分量分别为:

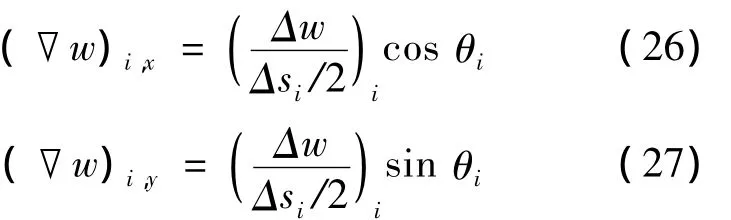
式中:θi为控制体中心连线与x轴正向的夹角.

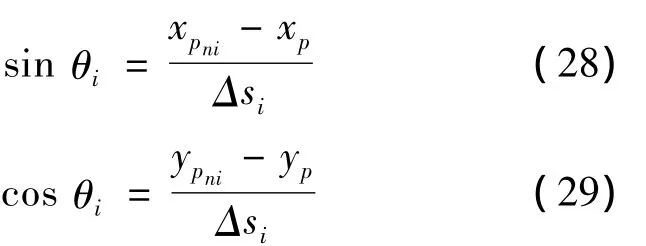
采用基元中心法，求得:

m为相邻控制体个数，得到粘性系数的离散式为:

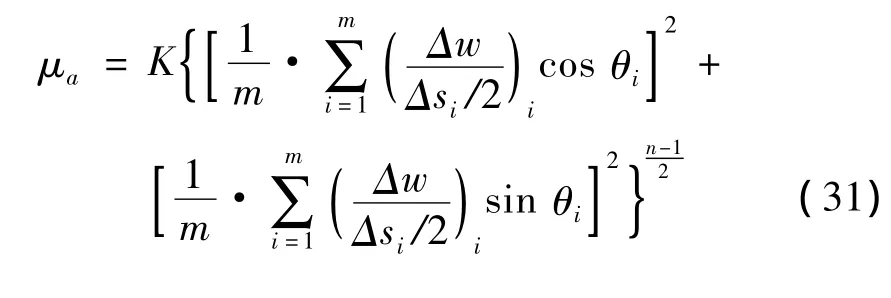
3 计算结果及分析

文中选用的非牛顿流体模型剪切应变力与剪切应变存在幂函数关系，即Ostwald-de Waele关系式:

式中:K是物性系数，n为幂律因子.选取n=0.6，0.8，1.0的剪切稀化流体，在半径比r*=0.5，偏心率分别为ε*=0.2，0.5，0.8的偏心圆环管中进行数值计算分析.

3.1 偏心圆环中非牛顿流体流动数值计算

图3为n=0.6的剪切稀化流在ε*=0.2，0.5，0.8，r*=0.5的圆环管中的等速线分布图.从图中对比可以看出偏心率造成流体速度分布不均，且随着偏心率的逐渐增大，位于流道截面较窄区域的流体速度逐渐减少为零，而流道截面较宽区域的流体流动速度逐渐增大.

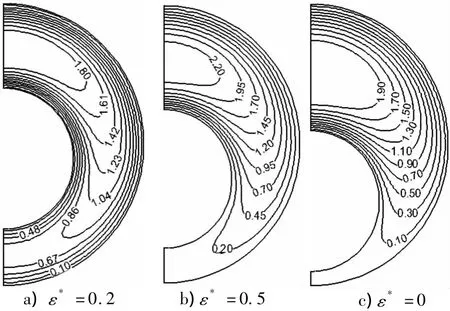
图3 幂律因子n=0.6的非牛顿流体在不同偏心圆环管中流动等速线分布图Fig.3 Distribution of isovels in different eccentric annular channels(n=0.6)

图4为不同幂律因子的非牛顿流体在r*=0.5，ε*=0.8的偏心圆环管较宽区域对称轴上的速度分布图.图中横坐标通过公式(33)由偏心圆环管较宽区域对称轴上的纵坐标转换得到的.图中流道较窄区域(窄域)的速度趋近为零.而流体速度在较宽区域(宽域)的二分之一半径处达到最大值，且速度分布曲线的斜率随着幂律因子减小而减小，这也反应了非牛顿流体粘性系数随着速度梯度的增大而减小.

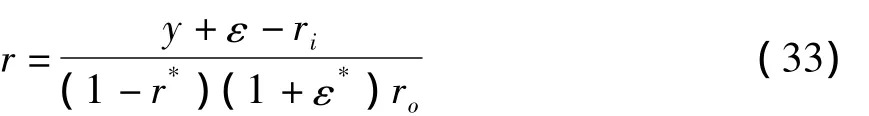
图5为ε*=0.2的偏心圆环管窄域和宽域对称轴线上的速度分布曲线.从图中可以看出不同幂律因子的非牛顿流体在流体通道窄域与宽域的速度分布曲线相似，最大速度都是随着幂律因子n减小而减小，速度分布斜率也是随着幂律因子的减小而减小.分析比较图4，5可得，随着偏心率的减小，流体通道宽域的速度逐渐减小，而窄域的速度则逐渐增大，最终会回归均匀分布，原因是随着偏心率逐渐减小，流体逐渐由宽域回流到窄域.

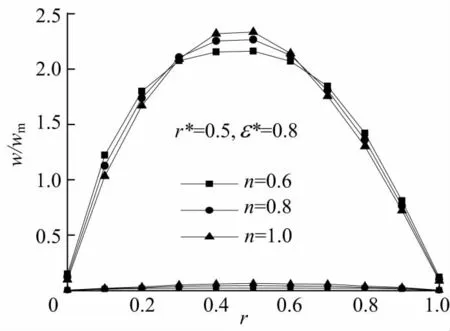
图4 不同幂律因子非牛顿流体在偏心圆环管对称轴上的速度分布曲线Fig.4 Distribution of flow velocity along the symmetry axis

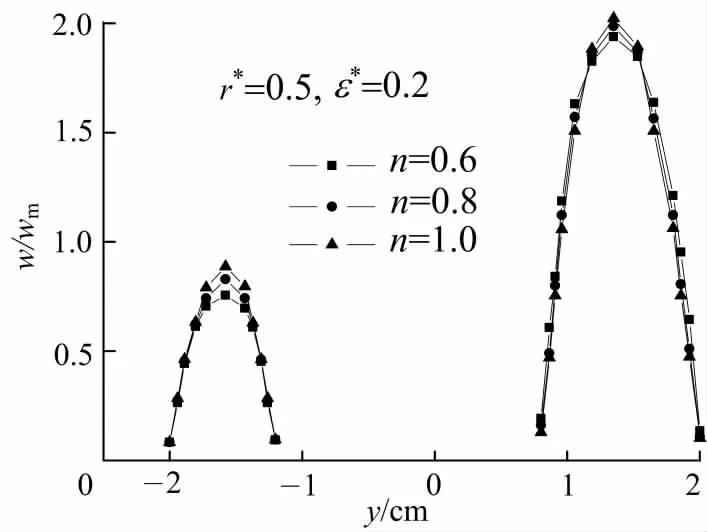
图5 ε*=0.2时，窄域和宽域对称轴线上的速度分布曲线Fig.5 Distribution of flow velocity along the symmetry axis in narrow area and wide area

3.2 非牛顿流体传热数值计算

图6为n=0.6的非牛顿流体在偏心率ε*=0.2，0.5，0.8，半径比 r*=0.5 的圆环通道中的等温线分布图.从图中可以看出随着偏心率的增大，偏心圆环管流道横截面宽域的温度逐渐降低，且等温线分布曲线相对稀疏.

图7为n=0.6，0.8，1.0的幂律非牛顿流体在r*=0.5，ε*=0，0.2，0.5，0.8 的 4 个圆环管中的温度分布比较图.图中横轴负值区域为偏心圆环管横截面窄域，正值区域为偏心圆环管宽域.从图中分析可得，同心圆环管(ε*=0)的温度分布均匀，而偏心圆环管中，随着偏心率的增大流体通道窄域的温度趋近于零，流体通道宽域的温度也逐渐降低，温度梯度也在逐渐增大，原因是偏心率的增大使得流体速度分布不均匀，从而使流体传热性能降低.

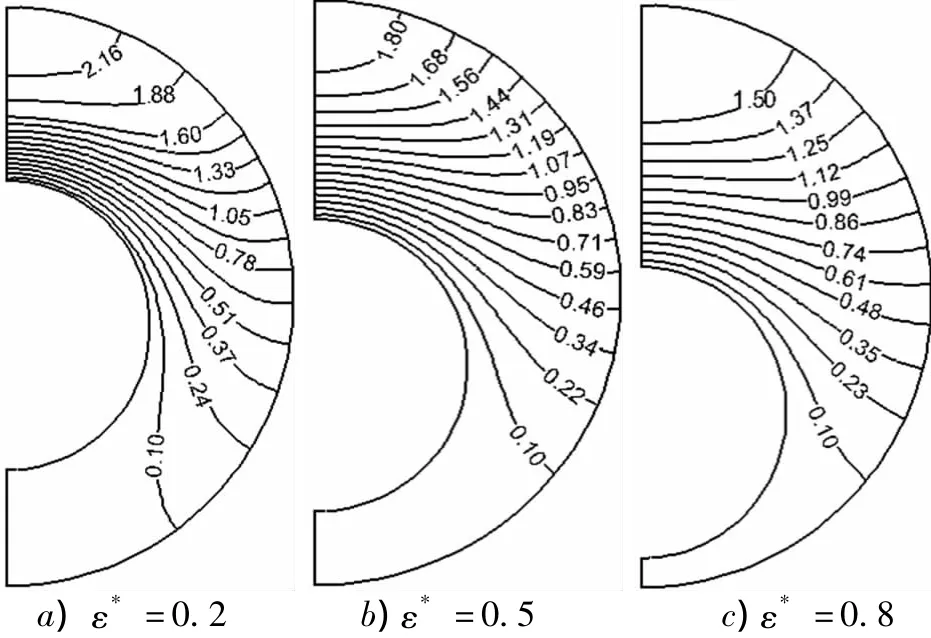
图6 幂律因子n=0.6的非牛顿流体在偏心圆环管中等温线分布Fig.6 Distribution of isotherm in different eccentric annular channels(n=0.6)

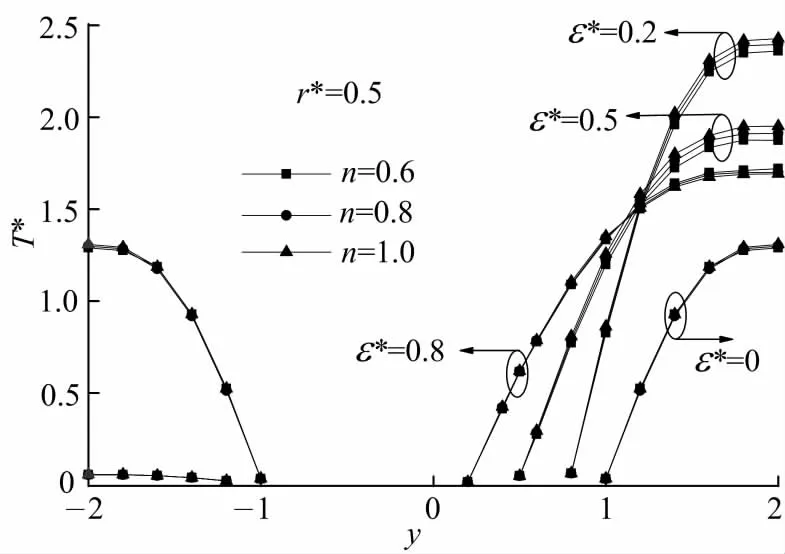
图7 非牛顿流体在不同偏心率的圆环管中的温度分布比较Fig.7 Distribution of temperature along the symmetry axis in different eccentric annular channels(n=0.6)

对于幂律因子对传热的影响，在同心圆环管中，流场温度分布几乎不受流体幂律因子影响，而在偏心圆环管中，幂律因子对流场的温度分布产生比较大的影响，这种影响在偏心率大于0.8时，几乎可以忽略，而在偏心率小于0.8时，流场的温度梯度变化才随幂律因子的增大逐渐显现出来.

表1为不同偏心圆环管中的无量纲努塞尔特数(Nu).从表中数据分析可得，同心圆环管中幂律因子的变化对努塞尔特数几乎不产生影响.而在半径比和偏心率较大的偏心圆环管中，幂律因子对努塞尔特数(Nu)的影响比较明显，Nu随n逐渐增大，这也验证了流体幂律因子对温度分布的影响受到偏心率和半径比的影响.从表中数据整体分析，努塞尔特数Nu随着偏心率和半径比的增大而减小，这说明较大的偏心率和半径比使流体在偏心圆环管中的传热性能降低.

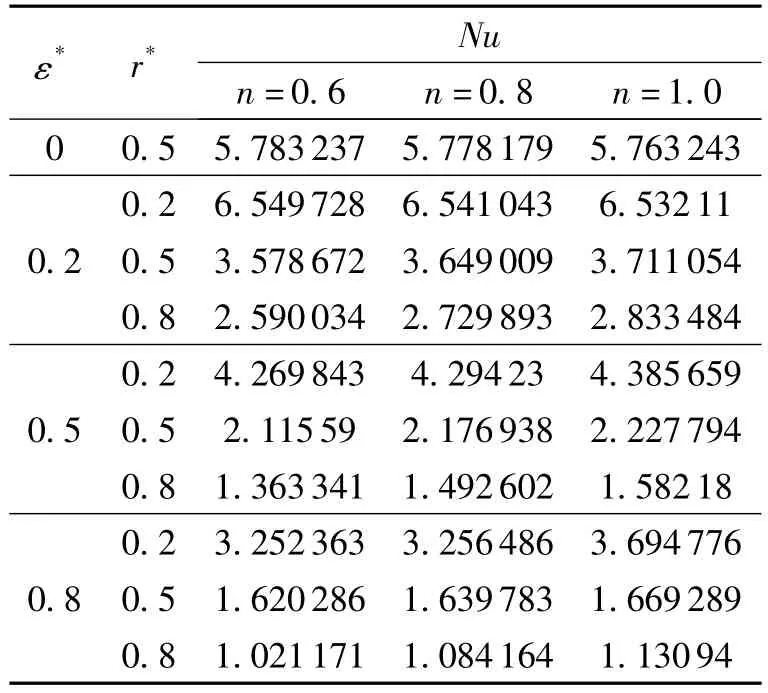
表1 非牛顿流体在不同偏心圆环管中无量纲努塞尔特数(Nu)值Table 1 Dimensionless nusselt number in different eccentric annular channels

4 结论

对偏心圆环管中幂律非牛顿流体的流动和传热进行了数值计算.得到以下结论:

1)偏心率是造成偏心圆环管内流体速度分布不均的主要原因，偏心率的增大导致宽域和窄域的速度分布极不对称，宽域速度增大，窄域速度趋于停滞.

2)非牛顿流体在流道横截面较窄区域与较宽区域的速度分布曲线相似，最大流速和速度分布斜率随幂律因子的减小而减小.

3)在偏心圆环管中，偏心率的增大使流场温度逐渐降低，温度梯度和努塞尔特数Nu也逐渐减小.说明偏心率对偏心圆环管中的流体传热性能有着比较大的不利影响.

4)幂律因子对偏心圆环管内温度分布的影响受到偏心率的影响，且这种影响随着偏心率的增大先增强后减弱，这个偏心率临界值处于0.8附近.

References)

［1］ 袁世伟，赖焕新.幂律非牛顿流体的有限体积算法［J］.华东理工大学学报:自然科学版，2013，39(3):364－369.Yuan Shiwei，Lai Huanxin.A finite volume method for calculating flows of power-law non-newton fluids［J］.Journal of East China University of Science and Technology:Natural Science Edition，2013，39(3):364 －369.(in Chinese)

［2］ 尹析明.环形套管内非牛顿流体非定常旋转流动谱方法研究［J］.四川大学学报:自然科学版，2009，46(4):1016－1020.Ying Ximing.Research on analytical approach to timedependent rotation flow of non-Newtonian fluid in the pap between cylinders［J］.Journal of Sichuan University:Natural Science Edition，2009，46(4):1016 －1020.(in Chinese)

［3］ 沈丹丹，朱宏武，丁矿，等.水下卧式采油树内部环空通道的流动特性分析［J］.石油机械，2014，42(2):42－44.Shen Dandan，Zhu Hongwu，Ding Kuang，et al.Analysis of the flow characteristic of the annular channel in sub sea horizontal christmas tree［J］.China Petroleum Machinery，2014，42(2):42 －44.(in Chinese)

［4］ 姚寿广，程清芳，王公利，等.以泡沫金属为吸液芯的纳米流体热管传热性能试验研究［J］.江苏科技大学学报:自然科学版，2013，27(6):556 －560.Yao Shouguang，Cheng Qingfang，Wang Gongli，et al.Experimental investigation on heat transfer performance of foam metal wick heat pipe［J］.Journal of Jiangsu U-niversity of Science and Technology:Natural Science E-dition，2013，27(6):556 －560.(in Chinese)

［5］ Nobari M R H，Mehrabani M T.A numerical study of fluid flow and heat transfer in eccentric curved annuli［J］.International Journal of Thermal Sciences，2010，49:380－396.

［6］ Bartosik B.Application of rheological models in prediction of turbulent slurry flow［J］.Flow Turbulence Combust，2010，84:277 －279.

［7］ Ho C J，Lin Y H，Chen T C.A numerical study of natural convection in concentric and eccentric horizontal cylindrical annuli with mixed boundary conditions［J］.International Journal of Heat Fluid Flow，1989，10(1):40－47.

［8］ Patankar S V.Numerical and heat transfer fluid flow［M］.Washington D.C:Hemisphere，1980.

［9］ Zhang M.Modeling of radiative heat transfer and diffusion processes using unstructured grid［D］.USA:Tennessee Technological University，2000.

［10］ Fang P P，Manglik R M，Jog M A.Characteristics of laminar viscous shear-thinning fluid flows in eccentric annular channels［J］.Journal of Non-Newtonian Fluid Mechanics，1999，84:1 －17.