新型二元混合制冷剂(R290＋R227ea)气液相平衡研究

陈秀萍 祁影霞 赵胜喜 张华

(上海理工大学能源与动力工程学院 上海 200093)

新型二元混合制冷剂(R290＋R227ea)气液相平衡研究

陈秀萍 祁影霞 赵胜喜 张华

(上海理工大学能源与动力工程学院 上海 200093)

混合制冷剂气液相平衡数据是新型制冷剂的热力学参数的重要组成部分。理论预测和实验测定混合工质的气液相平衡数据成为研究混合工质替代问题的一项迫切需要。本文基于量子化学理论，采用真实溶剂似导体模型(COSMO-RS)模拟了二元混合制冷剂(R290＋R227ea)气液相平衡性质，模拟的结果与实验结果有很好的一致性。表明运用COSMO-RS模型预测混合制冷剂的气液相平衡是可行的。

气液相平衡；量子化学；COSMO-RS；R290＋R227ea

近些年，在《联合国气候变化框架公约》和《京都议定书》的基础上，加速推动温室气体减排、减缓全球变暖趋势的呼声日益高涨[1]。要开发一种新型的制冷剂，首先要从热物性方面入手，气液相平衡性质是混合物最基本的热力学性质，是其他热力学性质的研究基础。国际上已经发展多种气液相平衡实验方法，如循环法，静态法，外推法等。

我国清华大学侯树鑫，段远源研究员采用循环法建立高精度气液相平衡实验系统测定了R125＋R290 在263.15 K，293.15 K，323.15 K下的性质。实验测定不仅实验系统结构复杂，实验设备和操作环节较多，对于有毒性、易爆性或其他有害物质，用实验方法测量热力学性质也很难行得通[2]。除实验法外，通过状态方程结合混合原则计算某些混合工质热物性。中国科学院理化技术研究所的公茂琼等[3]采用nonrandom-two-liquid activity coefficient(NRTL)模型，Peng-Robinson(PR)状态方程结合Huron-Vidal(HV)混合原则研究R1234ZE＋R290的气液相平衡性质。张宇等[4]利用同样的方法研究了二元混合制冷剂R170＋R116，并将计算结果与实验结果比对。而韩国首尔国立大学的Ju Hyok Kim等[5]将PR状态方程与van-der-waols混合原则结合计算了环保型制冷剂CO2＋R290在温度253.15 K～323.15 K的气液相平衡，法国的 Christophe Coquelet等[6]研究了 R32＋R227ea混合制冷剂温度从283.03 K～363.21 K的气液相平衡。Hao Guo等[7]通过实验测定与状态方程结合相比较研究了混合制冷剂R152a＋R134在温度258.15 K～288.15 K的气液相平衡。法国的F. Rivollet等[8]利用静态分析法实验测定CO2＋R32在温度283.12 K～343.25 K，压力最高达7.46 MPa下的气液相平衡。近年，因为层出不穷的新物质使得状态方程法越来越受限制，而计算机技术的发展，计算机模拟的优势也越来越明显。赵胜喜等[9]利用吉布斯蒙特卡罗模拟了R410A的气液相平衡并得到其临界状态点。意大利里雅斯特大学化学系的 Oliver Milocco等[10]列举了部分制冷剂利用COSMO-RS与分子动力学模拟两种方法预测热物性。赵胜喜[11]等通过分子动力学模拟饱和液态制冷剂氨的热物理性质(比焓＋密度)。相比较几种模拟方法，COSMO-RS它绕开了势能函数及其参数的选择，仅依赖于单个分子的结构，因而具有较高的理论精度，是一种新颖的统计热力学方法。

本文基于以上现状分析，结合前人已研究的成果，尝试模拟分析了两种新型二元混合制冷剂(R290 ＋R227ea)的气液相平衡性质，采用由 Andreas Klamt[12]1995年提出的真实溶剂似导体屏蔽模型(Conductor like Screening Model for Realistic Solvents)，简称COSMO-RS。是一种基于分子的量子化学计算信息结合统计力学理论进行物质的热物性计算的方法。该方法只需要物质单个分子的结构信息，就可以预测物质的热物性，是目前量子力学世界和工程热力学联系最有效的途径。

1 COSMO-RS模拟原理

1.1 COSMO-RS概念

COSMO是一种连续介质溶剂化模式[13－15]，模型中将连续介质的介电常数设为无穷大(理想导体)，这样可以将屏蔽电荷限制在界面上，从而分子和溶剂间没有电场，导体内没有电荷。在COSMO基础上计算表面屏蔽电荷密度，再结合统计力学方法得到各组分的化学势，最终计算获得其他物理性质如剩余焓、熵、蒸汽压等。COSMO-RS通过对单个分子的量子化学计算来预测多元体系的相平衡[16]。下面介绍预测流体(R290＋R227ea)气液相平衡热物性方面的应用。

1.2 σ-profile

分子表面的屏蔽电荷密度是采用COSMO-RS理论最重要的数据。因为我们要描述的真实体系都没有真实的面，为了描述真实体系，我们必须引入一个虚拟的分子间相互作用的节，并且这些节要有一定的表面积，每个节的表面屏蔽电荷能用一个合适的平均值进行表示，能满足相互配对。我们可以采用量子化学方法得到这些节的表面电荷密度，得到一种类型分子的有效概率函数p(σ)，称为分子的“σ-profile”，它表示在一个相互接触的分子节上面计算得到平均屏蔽电荷密度σ的概率，由量化计算产生，经过一个基于下述公式的半径γαν的面积上的系综平均步骤:

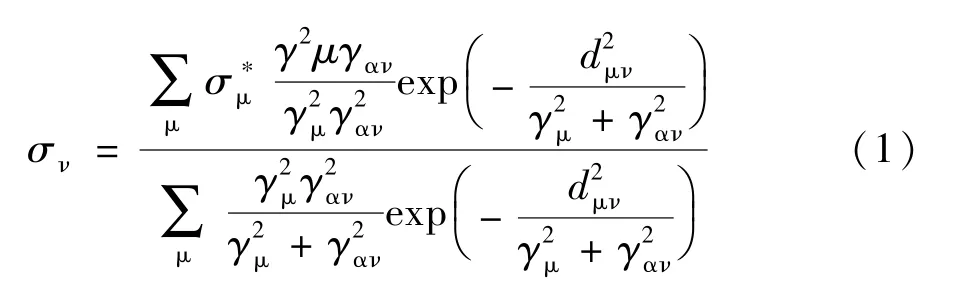
式中:dμυ为片段μ和υ之间的距离；γμ为根据片段面积计算得片段μ的平均半径；γαυ为可调节参数。

然后通过电荷平均得到σ-profile。分子i的σprofile定义为:

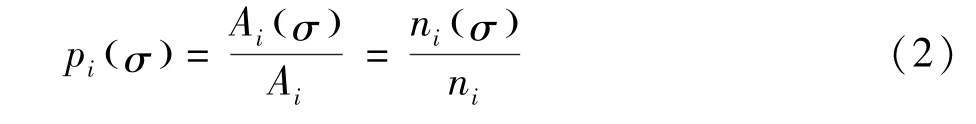
式中:Ai(σ)为电荷密度为σ的所有片段的总表面积；Ai为总空穴表面积；ni(σ)为电荷密度为σ的片段数量；ni为总片段数。

对于混合物，发现具有屏蔽电荷密度为σ的片段的几率ps(σ)，由体系中各种组分i的σ-profile，pi(σ)及其摩尔分数xi加权平均得到:

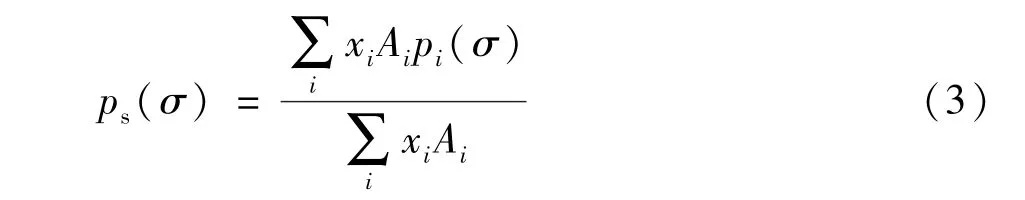
2 COSMO-RS模拟步骤

量化计算时可同时得到分子的表面积(molecular surface)Ai和总的空腔体积(cavity volume)Vi，上述信息可用于计算活度系数的组合部分；通过解自恰方程可得到片段活度系数，混合物中物质的活度系数的剩余部分可从片段活度系数得到。下面详细介绍R290＋R227ea的模拟步骤。

2.1 σ-profile

分子表面被分成若干面积为aeff的小块，这些小块相互之间是相互独立的，每个小块的表面屏蔽电荷是由量子化学中COSMO方法计算得到的。图1，图2分别是COSMO计算得到的R290，R227ea的σ-profile；图3，图4分别是直观COSMO表面电荷密度。

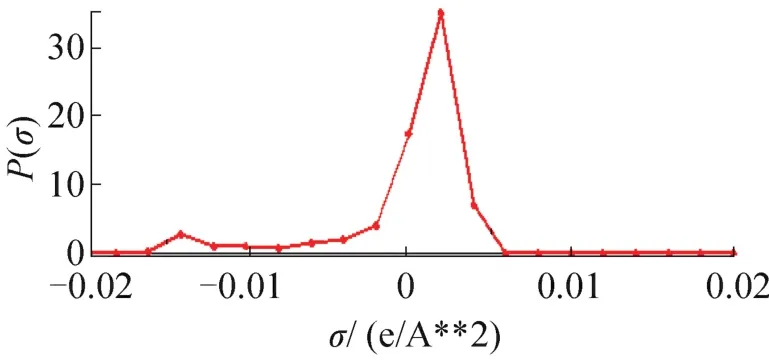
图1 R290的σ-profileFig.1 σ-profile of R290

2.2 COSMO-RS表面电荷的相互作用

COSMO-RS理论的分子间相互作用力是根据分子表面片段的相互作用上得到的。对于理想的屏蔽分子，如果两个节所带的表面密度电荷一正一负，则它们的相互作用能肯定为零。实际上这种所有分子的理想配对是不可能的。对于实际流体，我们往往采用相互接触的片段对的净屏蔽电荷密度σ1和σ2来计量两个节在真实体系和理想体系中的能量差别(misfit energy):

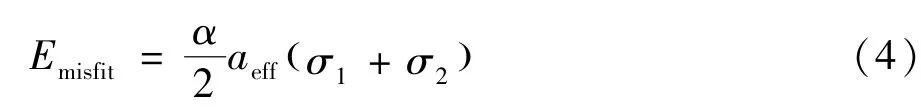
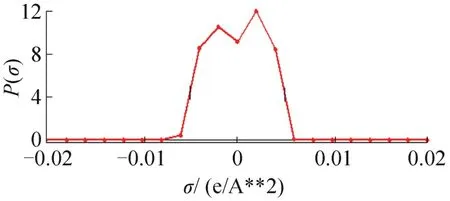
图2 R227ea的σ-profileFig.2 σ-profile of R227ea

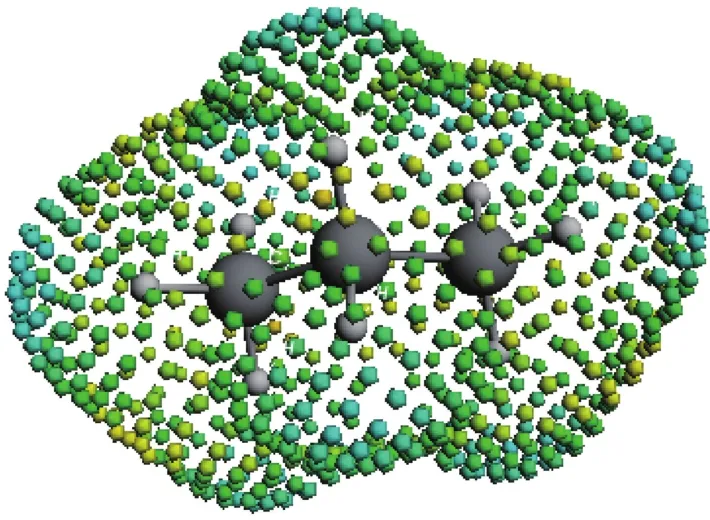
图3 R290的COSMO表面电荷密度Fig.3 COSMO surface charge density of R290

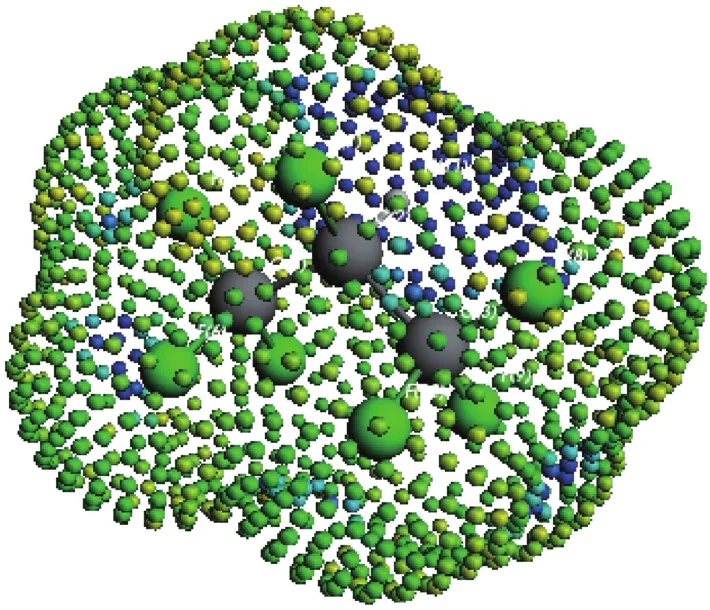
图4 R227ea的COSMO表面电荷密度Fig.4 COSMO surface charge density of R227ea

如果我们研究的体系是强极性物质，我们还应该考虑氢键的相互作用，Klamt和Eckert也提出了计算氢键相互作用的简单表达式:

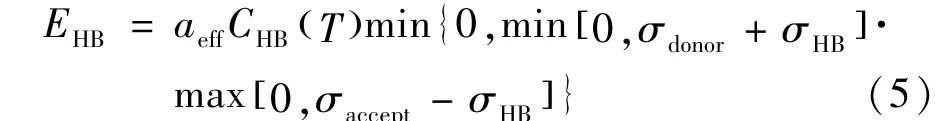
式中:σdonor＝min[σ1，σ2]，σaccept＝max[σ1，σ2]。CHB和σHB都是可调参数。

另外，分子间的作用力，除了考虑Emisfit和EHB之外，还考虑了分子片段间的范德华相互作用力Evdw:

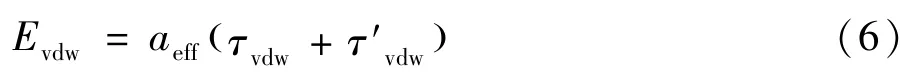
上式中的τvdw和τ′vdw都是基本元素的可以调节的参数。范德华的作用能量与组成物质的原子类型有关。

总的分子相互作用能量可由下式得出:

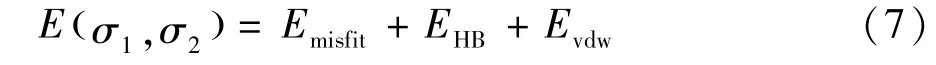
在得到分子间相互作用能量之后，经过一系列严格的统计热力学理论计算，可以得到系统中各组分的化学势。在此基础上，计算工程需要的热物理性质。

2.3 二元混合物气液相平衡数据

由于大多数制冷工质的压力不高，我们可以把它们的气相状态看做理想状态，对于二元体系，由相平衡的热力学关系可以得到:

式中:psat1和psat2为纯组分1和纯组分2的饱和蒸汽压；ptotal为系统的总压力；x1和x2为组分1和组分2在液相的摩尔分数；γ1和γ2为采用COSMO-RS方法预测的组分1和组分2的活度系数。

根据道尔顿分压力定律，组分1的分压力可用下式表示:

式中:y1为组分1在气相中的摩尔分数。

根据拉乌尔定律，组分1的分压力也可用下式表示:

联立上面三式可得，气液相平衡时组分1在汽相中的摩尔分数:

二元共沸体系中，共沸点处的压力对组分的一阶导数为0，即:

定义COSMO-RS模拟值与实验[15]数据相对误

差:

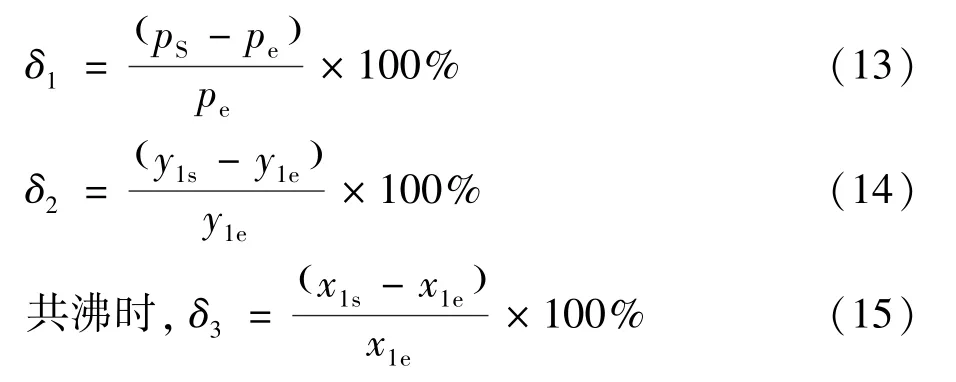
式中:ps为COSMO-RS模拟压力值，MPa；pe为实验[17]压力值，MPa；y1s为组分R290(1)气相COSMO-RS模拟物质的量，mol；y1e为组分R290(1)气相实验[17]物质的量，mol；x1s为组分R290(1)液相COSMO-RS模拟物质的量，mol；x1e为组分R290(1)液相实验[17]物质的量，mol。

3 R290＋R227ea气液相平衡模拟结果

HFO-227ea，1，1，1，2，3，3，3—·—七氟丙烷(R227ea)是国际上最近提出的一种新的不破坏臭氧层的替代物，已被作为灭火剂用于替代哈龙，并被认为是一种很有希望的制冷剂替代物，尤其是作为混合物的一种组分用于R502和R22的替代。R290，丙烷C3H8，分子量44.9，沸点－42.2℃，ODP＝0，GWP＝0.01，可用于替代R22，R502，是一种环保型制冷剂。基于国内外行情，不仅对臭氧层空洞问题日益关注，温室效应也越来越受到广泛重视，丙烷以其极小的GWP以及零值ODP，低沸点的优势被研究者用来探索新型制冷剂。但是因为它易燃易爆，须添加阻燃剂降低其燃爆可能性，R227ea是理想的灭火剂，本文尝试将这两种制冷剂混合研究了定温下(293.16 K，303.15 K，313.14 K，333.15 K，343.16 K，353.188 K)气液相平衡时的总压力p(MPa)随组分R290(1)的变化，分析利用COSMO-RS模型预测制冷剂热物性的可行性。用于替代现行个别的具有较高GWP的中温制冷剂。模拟结果如下表1所示，由模拟结果可知，混合制冷剂在209.16 K～353.18 K下气液相平衡时压力的最大相对误差在4.5%内，共沸点处的组分1摩尔分数最大相对误差在4%。总体看来，虽然有些偏差，但是从图5，图6可以看出与文献[17]提供的实验数据具有很好的一致性。另外，图表说明该模型在低温吻合的更好，如何改进高温部分还值得进一步研究。

实线:COSMO-RS模拟数值结果；散点:实验[17]数据。根据图表，找到不同温度下，R290＋R227ea的共沸点，结果如表2，图7所示，与实验[17]测得的值误差在4%内，证明了该模拟方法在预测气液相平衡具有一定的可行性。

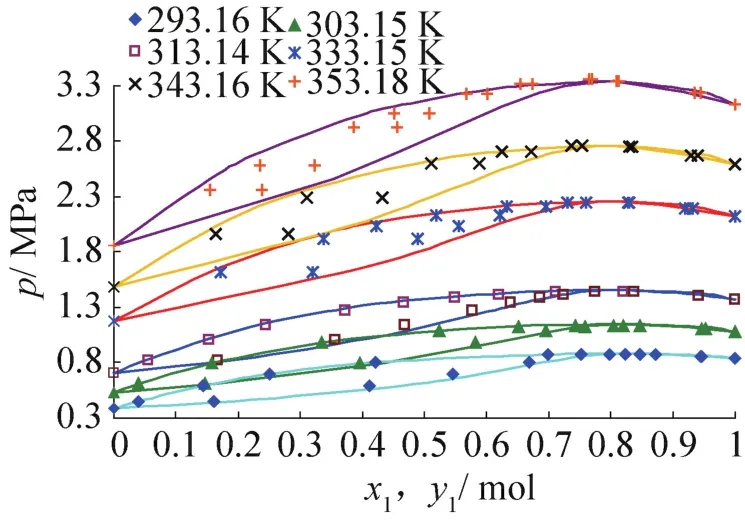
图5 制冷剂(R290＋R227ea)的气液相平衡热物理性质Fig.5 Vapor-liquid equilibrium thermodynamic properties of refrigerant R290＋R227ea

图6 制冷剂(R290＋R227ea)的气液相平衡压力模拟与实验值相对误差Fig.6 Deviations of the pressure between the experiment data and the simulation of refrigerant(R290＋R227ea)

图7 制冷剂(R290＋R227ea)的共沸点模拟与实验值相对误差Fig.7 Deviations of the azeotropic composition x1and pressure p between the experiment data and the simulation of refrigerant(R290＋R227ea)

4 结论

本文基于Kalmt等人提出量子力学理论，采用真实溶剂似导体屏蔽模型，模拟新型二元混合制冷剂(R290＋R227ea)在293.16 K～353.18 K温度下气液相平衡的热物理性质，模拟结果压力及共沸点数据证实与实验值相对误差控制在4%以内，有很好的一致性，表明该模型可以计算混合制冷工质的气液相平衡性质。

表1 制冷剂(R290＋R227ea)的气液相平衡热物理性质Tab.1 Vapor-liquid equilibrium thermodynamic properties of refrigerant(R290＋R227ea)

333.15 K 0.5194 2.1312 2.1490 0.84 0.6214 0.6776 9.04 0.6331 2.2110 2.2141 0.14 0.6956 0.7268 4.49 0.7304 2.2450 2.2450 0.00 0.7596 0.7679 1.09 0.8283 2.2430 2.2520 0.40 0.8296 0.8178 －1.42 0.9316 2.1892 2.2100 0.95 0.9197 0.8987 －2.28 1.0000 2.1168 2.1168 0.00 1.0000 1.0000 0.00 343.16 K 0.0000 1.4874 1.4874 0.00 0.0000 0.0000 0.1637 1.9623 2.0331 3.61 0.2801 0.3792 35.38 0.3110 2.2891 2.3610 3.14 0.4327 0.5396 24.71 0.5108 2.5976 2.6220 0.94 0.5890 0.6649 12.89 0.6246 2.7060 2.7038 －0.08 0.6713 0.7170 6.81 0.7369 2.7579 2.7468 －0.40 0.7540 0.7671 1.74 0.8341 2.7505 2.7512 0.03 0.8303 0.8196 －1.29 0.9401 2.6709 2.6897 0.70 0.9285 0.9099 －2.00 1.0000 2.5868 2.5868 0.00 1.0000 1.0000 0.00 353.18 K 0.0000 1.8583 1.8583 0.00 0.0000 0.0000 0.1541 2.3607 2.4593 4.18 0.2374 0.3529 48.66 0.2343 2.5808 2.6925 4.33 0.3236 0.4552 40.67 0.3865 2.9276 3.0134 2.93 0.4565 0.5846 28.06 0.4511 3.0486 3.1089 1.98 0.5078 0.6244 22.96 0.5681 3.2264 3.2340 0.24 0.6011 0.6851 13.97 0.6538 3.3157 3.2934 －0.67 0.6729 0.7249 7.73 0.7653 3.3629 3.3317 －0.93 0.7690 0.7785 1.24 0.8119 3.3391 3.3390 0.00 0.8096 0.8048 －0.59 0.9450 3.2341 3.2430 0.28 0.9354 0.9167 －2.00 1.0000 3.1319 3.1319 0.00 1.0000 1.0000 0.00

表2 组分1R290在共沸点的摩尔数及气液相平衡压力Tab.2 The azeotropic composition x1and pressure p for R290＋R227ea at each temperature

[1] 贾磊，史敏，张秀平，等.合成类HCFCs替代制冷剂的研究进展[J].制冷与空调，2011，2(1):116-120.(Jia Lei，Shi Min，Zhang Xiuping，et al.The advanced developments of alternative refrigerants as anabolic HCFCs[J].Refrigeration and Air-condition，2011，2(1):116-120.)

[2] 侯树鑫，段远源.高精度气液相平衡实验系统的建立和实验测定[J].工程热物理学报，2009，30(7):1093-1097.(Hou Shuxin，Duan Yuanyuan.The establishment and the experimental measurement of vapor-liquid equilibrium experimental system with high-precision[J].Journal of Engineering Thermophysics，2009，30(7):1093-1097.)

[3] Xueqiang Dong，Maoqiong Gong，Jun Shen，et al.Experimental measurement of vapor-liquid equilibrium for(trans-1，3，3，3-tetrafluoropropene(R1234ze(E))＋propane (R290))[J].International journal of refrigeration，2011，34:1238-1243.

[4] Yu Zhang，MaoQiong Gong，HongBo Zhu，et al.Vaporliquid equilibrium measurements and correlations for an azeotropic system of ethane＋hexafluoroethane[J].Fluid Phase Equilibria，2006，240:73-78.

[5] Ju Hyok Kim，Min Soo Kim.Vapor-liquid equilibria for the carbon dioxide＋propane system over a temperature range from 253.15 to 323.15 K[J].Fluid Phase Equilibria，2005，238:13-19.

[6] Christophe Coquelet，Alain Valtz，Dominique Richon.Vapor-liquid equilibrium data for the difluoromethane(R32) ＋dimethylether(RE170)system at temperatures from 283.03 to 363.21 K and pressures up to 5.5 MPa[J]. Fluid Phase Equilibria，2005，232:44-49.

[7] Hao Guo， Maoqiong Gong， XueqiangDong， etal. (Vapour＋liquid)equilibrium data for the azeotropic{1，1-difluoroethane(R152a)＋1，1，2，2-Tetrafluoroethane (R134)}system at various temperatures from(258.15 to 288.15)K[J].J.Chem.Thermodynamics，2012，54: 129-133.

[8] F Rivollet，A Chapoy，C Coquelet，et al.Vapor-liquid equilibrium data for the carbon dioxide(CO2)＋difluoromethane(R32)system at temperatures from283.12 to 343.25 K and pressures up to 7.46 MPa[J].Fluid Phase Equilibria，2004，218:95-101.

[9] 赵胜喜，祁影霞.制冷剂R410a的气液相平衡的吉布斯蒙特卡罗模拟[J].低温与超导，2012，40(3):69-72. (Zhao Shengxi，Qi Yingxia.Gibbs Ensemble Monte Carlo simulation of vapor－liquid equilibrium properties of R410a [J].Cryogenics and Superconductivity，2012，40(3):69-72.)

[10]Oliver Milocco，Maurizio Fermeglia，Sabrina Pricl.Prediction of thermophysical properties of alternative refrigerants by computational chemistry[J].Fluid Phase Equilibria，2002，199:15-21.

[11]赵胜喜，祁影霞.饱和液态制冷剂氨的热物理性质的分子动力学模拟[J].制冷学报，2012，33(1):32-34. (Zhao Shengxi，Qi Yingxia.Molecular dynamics simulation of thermodynamic properties of the saturated liquid ammonia[J].Journal of Refrigeration，2012，33(1):32-34.)

[12]Klamt A.Conductor-like screening model for real solvents: A new approach to the quantitative calculation of solvation phenomena[J].J.Chem.Phys.，1995，99:2224-2235.

[13]Klanlt A，Jonas V，Burger T，et al.Refinement and Parameterization of COSMO-RS[J].The Journal of Physical Chemistry，1998，102(26):5074-5085.

[14]Klamt A，Eckert F.COSMO-RS:a novel and efficient method for the a priori prediction of thermophysical data of liquids[J].Fluid Phase Equilibria，2000，172(1):43-72.

[15]李胜迎.醇＋(酮、离子液体)二元体系的过量焓测定、关联和COSMO-type模型的应用[D].浙江大学理学院，2008.

[16]Klamt A，Schuurmann G.COSMO:a new approach to dielectric screening in solvents with explicit expressions for the screening energy and its gradient[J].Journal of the Chemical Society，Perkin Transactions，1993，5:799-805.

[17]A Valtz，C Coquelet，A Baba-Ahmed，et al.Vapor-liquid equilibrium data for the propane＋1，1，1，2，3，3，3-heptafluoropropane(R227ea)system at temperatures from 293.16 to 353.18 K and pressures up to 3.4 MPa[J]. Fluid Phase Equilibria，2002，202:29-47.

Vapor-liquid Equilibrium Properties of New Binary Mixture Refrigerant(R290＋R227ea)

Chen Xiuping Qi Yingxia Zhao Shengxi Zhang Hua

(College of Energy and Power Engineering，University of Shanghai for Science and Technology，Shanghai，200093，China)

The vapor-liquid equilibrium data is an important part of thermodynamic parameters of a new refrigerant.Theoretical predictions and experimental measurements of vapor-liquid equilibrium data of a new mixed working fluid become an urgent need for alternative refrigerant researches.The article is based on the theory of quantum chemistry.The vapor-liquid equilibrium properties of binary refrigerant(R290＋R227ea)were modeled by COSMO-RS simulations.The simulation results could accord with the data of experiments well.It shows that COSMO-RS simulation method is feasible to predict the vapor-liquid equilibrium properties of mixture refrigerants.

vapor-liquid equilibrium；quantum chemistry；COSMO-RS；R290＋R227ea

TB61＋1；TK124

A

0253－4339(2014)05－0094－07

10.3969/j.issn.0253－4339.2014.05.094

陈秀萍，女(1989－)，在读硕士，上海理工大学能源与动力工程学院，18818251838，E-mail:shirley12141019＠126.com。研究方向:COSMO-RS预测新型替代制冷工质的热物性。

2013年11月22日

About the author

Chen Xiuping(1989－)，female，Master Candidate，College of Energy and Power Engineering，University of Shanghai for Science and Technology，18818251838，E-mail:shirley12141019＠126. com.Research fields:COSMO-RS studies of the thermodynamics properties of the new alternative refrigerant.