鲁棒Kalman滤波陀螺随机噪声AR快速/实时建模

黄 磊，赵亚琴

（南京林业大学机电学院自动化系，江苏 南京 210037）

鲁棒Kalman滤波陀螺随机噪声AR快速/实时建模

黄 磊，赵亚琴

（南京林业大学机电学院自动化系，江苏 南京 210037）

针对传统陀螺随机噪声的AR建模方法收敛速度慢、所需样本多等问题，提出新的基于鲁棒Kalman滤波的陀螺随机噪声AR建模方法。该方法将AR模型参数作为系统的状态量，采用未知时变的噪声统计估值器估计观测噪声的均值和方差，通过Kalman滤波估计出AR模型参数。实验结果表明：这种AR建模方法具有收敛速度快，时间开销少的优点。当有新的噪声数据到来时，还能使建立的AR模型得到及时更新，提高建模准确度，适用于快速建模或陀螺随机噪声具有强时变性的工程场合。

捷联惯性导航系统；陀螺随机噪声建模；鲁棒Kalman滤波器；时间序列

0 引 言

在捷联惯导和组合导航系统中，经常要对陀螺仪的误差建模，通过补偿手段提高陀螺仪的使用精度[1-3]。陀螺仪的输出误差由确定性误差（如零偏、刻度因数误差等）和随机误差构成。确定性误差一般可以通过实验标定的方法加以补偿。随机误差只能从信号处理的角度，建立误差的数学模型，继而采用滤波等手段消除。在这个过程中基于时间序列建模的方法得到了广泛应用。

当前对陀螺仪随机噪声的时间序列建模很多是基于AR（自回归）模型进行的[4-5]。传统的AR建模方法有最小二乘法、Yule-Walker方程估计法等，但这些传统的建模方法所需样本数据较多，且不能及时反映陀螺随机噪声的时变特性。为解决这一问题，本文提出了基于鲁棒卡尔曼滤波的陀螺随机噪声AR建模方法。

1 陀螺随机噪声的平稳随机性检验和定阶

对某国产MEMS(微电子机械)陀螺进行地面静态实验，所获得的噪声数据如图1所示（共50000点）。数据采样率为14Hz，单位：deg/s。经检验该数据含有一定的常值项（由地球自转角速度和陀螺的零偏等引起）。经一阶差分去除常值趋势项后，得到满足平稳随机性要求的随机噪声数据。分析该噪声的自相关和偏相关特性，发现自相关系数呈现出拖尾性，而偏相关系数在k=2后截断（如图2所示）。

根据时间序列分析理论，对于自相关函数呈现拖尾性而偏自相关函数呈现截尾性的平稳随机序列最适宜采用AR模型建模，且偏相关函数的截断处就是模型的阶数[6-8]。因此选择2阶AR模型建模最合适。

根据定义，AR（2）模型的数学描述为

式中ε（k）为均值为0方差未知的白噪声。

2 基于鲁棒Kalman滤波的AR模型建模方法

从式（1）可以看出，AR（2）模型的关键是根据观测量z（k）求出各回归项z（k-1）、z（k-2）的系数a1、a2。如果将a1、a2作为系统状态量，通过建立合理的状态方程和观测方程，就可使用Kalman滤波器得到a1、a2的准确估计。

图1 某国产MEMS陀螺的噪声数据

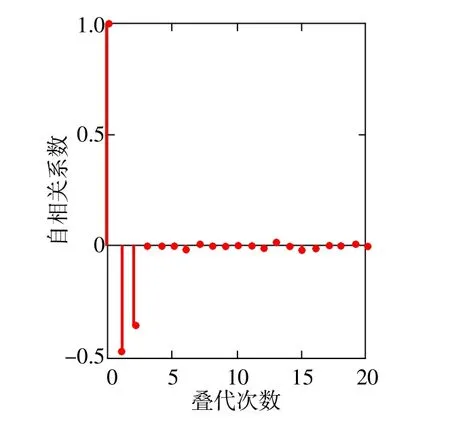
图2 陀螺随机噪声的偏相关函数

2.1 系统方程

将AR（2）模型系数a1、a2定义为系统的状态量：

则可把式（1）作为观测方程：

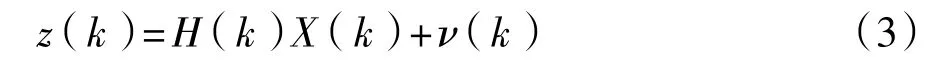
式中：H（k）=[z（k-1），z（k-2）]，ν（k）=ε（k）。

考虑到当陀螺仪的随机噪声特性稳定时，满足一定的样本数后，所建立的AR模型的参数应稳定收敛于真值，不再随样本数量的增加而增加。即1

把式（4）作为状态转移方程。则系统状态空间模型为

从式（5）可以看出，系统噪声w（k）为0，状态转移阵Φ=I。则有：

2.2 未知观测噪声的统计估值器

系统的观测噪声ν（k）主要由AR模型中的白噪声ε（k）引起。由于ε（k）的方差特性未知，所以观测噪声ν（k）属于统计特性未知的白噪声。在鲁邦Kalman滤波器中，通常采用带遗忘因子的噪声统计估值器估计未知噪声特性[6]。该方法在估计观测噪声时强调新数据的作用，对于时间上过于古老的数据则渐渐遗忘。即采用渐消的记忆指数加权方法实现对未知噪声的统计特性估计[6]：

式中b称为遗忘因子，一般取0.95＜b＜1。由Kalman滤波中的新息计算。

2.3 基于鲁棒Kalman滤波的AR模型快速建模

式（5）给出了系统的状态方程和观测方程，式（6）、式（7）给出了系统噪声和观测噪声的统计特性，该特性满足卡尔曼滤波器的要求。因此可以应用鲁棒卡尔曼滤波器对状态量，即AR（2）模型的2个参数进行估计。鲁棒卡尔曼滤波过程如下：

状态一步预测：

由于系统噪声为0，状态转移阵Φ=I。因此一步预测误差方差阵为

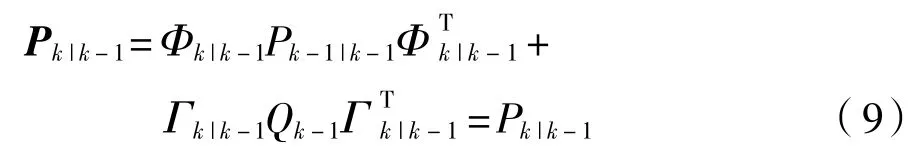
滤波增益矩阵为

新息为

状态估计为

估计误差方差阵为

图3中的虚直线是Y-W法对1 h采样数据的AR（2）模型建模结果：

采用新的基于鲁棒Kalman滤波的AR模型参数估计结果如图3中实曲线所示。在实际运行时，可以根据系统的建模精度要求设定阈值θ。如连续10次的运行迭代结果中，状态量估计值（也即1、2）的最大值和最小值之间的差异都小于该阈值θ，则认为状态估值已稳定收敛。考虑到一般AR模型的参数估计精确到小数点后3位已足够，这里选取θa1=θa2=0.001，则滤波器在运行2150次后满足条件退出，状态量估计收敛于：

图3 基于鲁棒Kalman的AR（2）建模结果

式（15）即是采用鲁棒卡尔曼滤波快速建模的结果，该过程仅需2150个样本。式（14）是采用传统Y-W对1 h样本数据的建模结果。对比两式可以看出，两者的建模结果非常接近，相对差异为δα1=4.9%，δα2=6.2%。由于在有限样本条件下，不同时间序列建模方法（如最小二乘法和Y-W法）的建模结果本就不会完全相同。这一波动在大多数工程允许的精度范围之内（＜10%）[6]。但新的建模方法的优势在于所用的样本数和实验时间大大减少（滤波器收敛退出即可结束），非常适用于需要快速对陀螺仪随机噪声建模的场合。

2.4 基于鲁棒Kalman滤波的AR模型在线实时建模

在某些需要极高精度或陀螺随机噪声特性强时变的场合，由外界环境等因素造成的陀螺仪随机噪声的时变性必须被考虑，这时传统固定参数式的建模方法已不能适用。而Kalman滤波器可以利用新的陀螺噪声观测数据对系统状态量，即AR模型的参数估计进行修正，使建立的AR模型参数能及时地跟踪陀螺随机噪声随时间的变化，从而获得更高的建模精度（但需注意在这种情况下Kalman滤波器的迭代退出时间只取决于需要建立的时变模型的时间长短，建模的优势体现在精度而非速度上）。

例如，对该陀螺的噪声数据分别采用新的基于鲁棒Kalman的AR在线实时建模方法和传统固定参数式Y-W法进行建模。并采用残差序列白化度检验法[9]对两种方法建模的结果进行检验。两种方法建模过程中得到的残差序列ε1（k）、ε2（k）的自相关函数如图4所示。可以看出，基于鲁棒Kalman的AR在线实时建模结果的残差序列ε1（k）比传统固定参数式

图4 两种AR建模方法对比

Y-W法的建模结果中的残差序列ε2（k）白化程度更好，更接近白噪声。因此说明建模的精度优于后者。

3 结束语

针对传统的陀螺随机噪声AR建模方法收敛速度慢、所需样本较多的缺点，本文提出了基于鲁棒Kalman滤波的AR模型建模方法。该方法将AR模型参数作为系统的状态量，采用带遗忘因子的噪声统计估值器估计系统观测噪声的均值和方差。通过Kalman滤波迭代快速经济的估计出样本的AR模型参数，减少了采样次数和实验时间。还能利用新的随机噪声信息实时修正AR模型参数，使参数估值能及时地反映和跟随陀螺仪随机噪声特性的变化，适用于要求快速建模或陀螺随机噪声具有强时变特性的工程场合。

[1]张庆，谈振藩，柳贵福，等.一种光纤陀螺随机漂移的非平稳时序建模法[J].传感器与微系统，2010，29（7）：43-46.

[2]张秋昭，张书毕，侯东阳.光纤陀螺随机漂移辨识方法研究[J].传感器与微系统，2011，30（9）：50-56.

[3]李家垒，许化龙，何婧.光纤陀螺随机漂移的实时滤波方法研究[J].宇航学报，2010，31（12）：2717-2721.

[4]陈俊杰，杨孟兴.光纤陀螺随机漂移时间序列建模研究[J].弹箭与制导学报，2011，31（5）：65-67.

[5]蒙涛，王昊，李辉，等.MEMS陀螺误差建模与滤波方法[J].系统工程与电子技术，2009，31（8）：1944-1947.

[6]严恭敏，李四海，秦永元.惯性仪器测试与数据分析[M].北京：国防工业出版社，2012：135-150.

[7]DrostF C，AkkerR V D，WerkerB J M.Efficient estimation of auto-regression parameters and innovation distributions for semip-arametric integer-valuedAR（p）models[J].Journal of the Royal Statistical Society:Series B（Statistical Methodology），2009，71（2）：467-485.

[8]Piet D J，Jeremy P.The ARMA model in state space form[J].Statistic&Probability Letters，2004，70（8）：119-125.

[9]李言俊，张科.系统辨识理论及应用[M].北京：国防工业出版社，2009：43-105.

Rapid/real-time AR modeling method for gyro random noise based on robust Kalman filter

HUANG Lei，ZHAO Ya-qin
（Mechanic and Electronic Engineering College，Nanjing Forestry University，Nanjing 210037，China）

To solve the problem of the traditional AR modeling methods for gyro random noise which need a large number of samples and can’t reflect the time-varying characteristic of the random noise timely，a new AR modeling method based on adaptive robust Kalman filter is developed.The AR model parameters are chosen to be the state variable.Unknown time-varying estimator of observation noise is used to achieve the estimates of the mean and variance of the observation noise.The AR model parameters can be estimated accurately by Kalman filter.Test results indicate that the new modeling method has the advantages of fast convergence and lowcost.When the new random noise samples are achieved，the Kalman filter can correct the model parameters timely.So the modeled AR parameters have high accuracy.The new modeling method can be applied to applications which need a rapid modeling or in which the gyro random noise has strong time-varying characteristic.

strapdown inertial navigation system；gyro random noise modeling；robust Kalman filter；time series

V241.5；TB535+.2；TN713；TN957.54

：A

：1674-5124（2014)06-0088-03

10.11857/j.issn.1674-5124.2014.06.023

2014-01-06；

：2014-03-01

国家自然科学基金项目（31200496）

黄 磊（1975-），男，安徽合肥市人，讲师，博士，研究方向为捷联惯性导航和嵌入式系统。