基于小波神经网络和PSO的动态误差溯源方法研究

邬肖敏，李世平，程双江

（第二炮兵工程大学，陕西 西安 710025）

基于小波神经网络和PSO的动态误差溯源方法研究

邬肖敏，李世平，程双江

（第二炮兵工程大学，陕西 西安 710025）

针对动态测试系统在测试过程中出现的精度损失问题，提出一种基于小波神经网络和粒子群优化算法相结合的动态误差溯源方法。该方法基于全系统动态精度理论，通过设计小波神经网络对动态测试系统的输出总误差进行分解，并采用粒子群优化算法对分解结果进行分析，追溯到误差产生的模块。仿真结果表明：该方法能够快速有效地完成误差溯源，并且溯源准确度达到10-2，具有可行性和应用性。

动态误差溯源；小波神经网络；粒子群优化算法；动态测试系统

0 引 言

测试设备的技术保障是对其进行计量检定工作的重要内容，一旦发现测试设备指标参数超差，说明其已经产生故障，应进行测试设备的维修。

目前，根据国家的计量检定规程，测试设备计量技术保障仅限于检测是否出现超差，只给出被检设备是否合格的结论；而对不合格的测试设备不进行超差原因（故障）的检测与分析，对于此类测试设备的事后管理和维修是亟待解决的问题。本文通过引入动态误差溯源的理论[1]对其进行研究，根据动态误差的分解结果找出产生误差的源头，从而对测试设备进行检定与维修。

动态误差溯源理论由合肥工业大学费业泰教授等提出，是在前人研究正向误差理论的基础上，深入研究测试系统内部组成结构，对动态测量误差理论和精度理论的研究，起着深化拓宽的作用。

1 动态误差溯源的基本原理

动态误差溯源建立在全系统精度理论[2-3]基础上，根据全系统传递链函数及误差的“白化”模型，将系统最后输出的总误差分解为各单项误差进一步追溯到动态测试系统内部产生该项误差的模块，并分析其误差特性。一旦实现了误差溯源，对测试系统的传输特性就有了深刻的了解，由此掌握系统各环节误差对其输出总误差的影响及其随时间的变化规律，并对系统的各个功能模块有较为清楚的认识。

1.1 基于全系统动态精度理论的测试系统及误差模型

根据全系统动态精度理论，典型的测试系统是一个混联式动态测试系统[4]，即测试系统中既包含串联，又包含并联，其结构如图1所示。

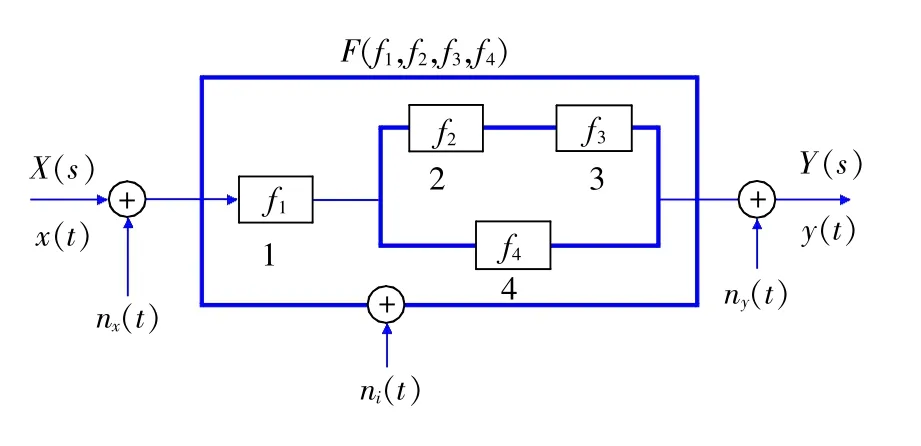
图1 混联式动态测试系统

图中，nx（t），ni（t），ny（t）表示外部环境对测试系统的干扰；f1（t），f2（t），f3（t），f4（t）分别代表模块1，2，3，4的传递函数；x（t），y（t）分别代表输入信号和输出信号。

不考虑外部干扰的情况下，根据建立的动态测试系统“白化”模型，动态测试系统输出总误差可表示为

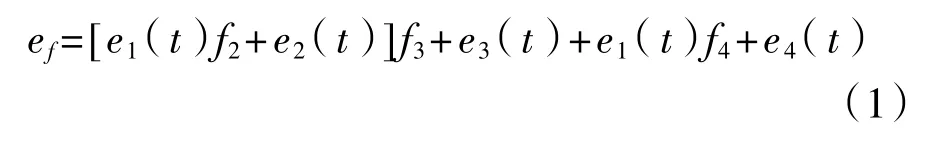
式中e1（t），e2（t），e3（t），e4（t）分别为各模块产生的误差。

1.2 基于小波神经网络的误差分解

对于动态误差信号的分解，本文采用广义小波神经网络[5-7]，即先通过小波分析将误差分解为多频段信号，设分解后的信号频率分别为f1，f2，f3，…，fl；再利用线性神经网络得出多频段信号的具体参数，一般周期信号都可以通过sin和cos函数叠加表示，所以设线性神经网络的输入为sin（fm）和cos（fm），m=1，2，3，…，l，输出为各个误差分量，进行数据拟合，得出权值矩阵w和阈值矩阵b，根据w和b即可确定误差分量的幅值大小。其过程如图2所示。

1.3 PSO算法基本原理

粒子群优化算法（particle swarm optimization，PSO）是一种进化计算技术，由Eberhart博士和Kennedy博士于1995年提出，它源于对鸟群捕食行为的研究。

PSO优化算法的基本思想是通过群体中个体之间的协作和信息共享来寻找最优解。

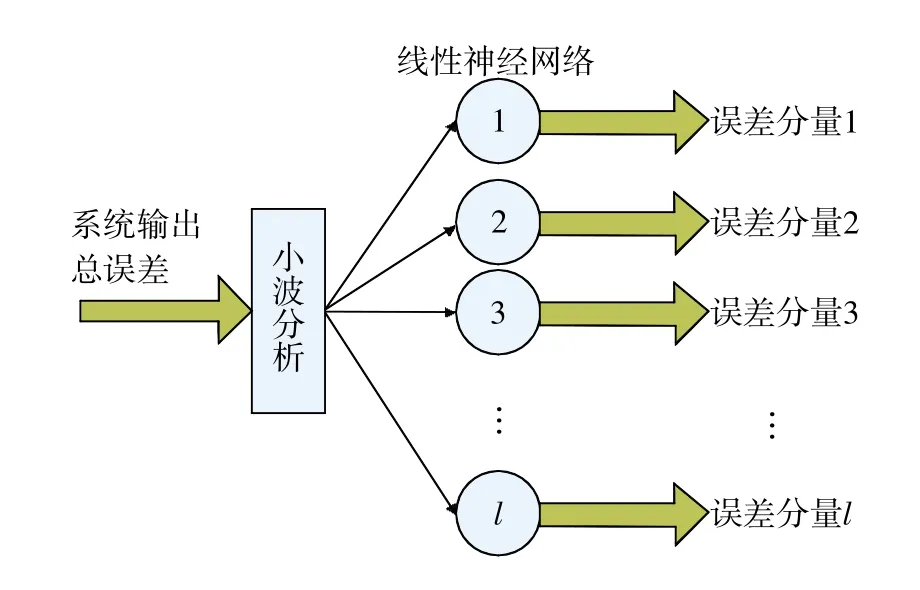
图2 基于小波神经网络的误差分解

假设在一个D维搜索空间中，由n个粒子组成的种群X=（X1，X2，…，Xn），其中第i个粒子表示一个D维的向量Xi=（Xi1，Xi2，…，XiD）T，代表第i个粒子在D维搜索空间中的位置，根据目标函数即可计算出每个粒子位置Xi对应的适应度值。第i个粒子的速度为Vi=（Vi1，Vi2，…，ViD）T，其个体极值为Pi=（Pi1，Pi2，…，PiD）T，种群的群体极值为Pg=（Pg1，Pg2，…，PgD）T。在每次迭代过程中，粒子通过个体极值和群体极值更新自身的速度和位置，即：

式中：ω——惯性权重；

d=1，2，…，D；i=1，2，n；

k——当前迭代次数；

Vid——粒子的速度；

c1、c2——非负常数，称为加速度因子；

r1、r2——分布于[0，1]区间的随机数，为防止粒子的盲目搜索，一般建议将其位置和速度限制在区间[-Xmax，Xmax]、[-Vmax，Vmax]内。

1.4 基于PSO的误差溯源

基于全系统动态精度理论，若动态测试系统内部有N个模块，则每个粒子的搜索空间维数设为N维，根据PSO算法，粒子数一般设为20～40个，对于某些复杂问题可以设置为100～200个。系统输出总误差经小波神经网络可分解为各单项误差，结合已知的动态测试系统各模块的传递函数，可以确定各个模块的误差范围。设各个模块产生的误差范围分别为[则粒子群的搜索空间确定。粒子群的搜索速度要根据搜索空间的范围进行调整，一般在[-1，1]之间取值。已知各项参数的范围，即可设定粒子的初始值，将粒子参数代入动态测试系统，结合训练样本数据计算出输出总误差的均方差mse（k），即粒子群优化算法的适应度值

式中：k——粒子群迭代次数；

ef——动态测试系统输出误差。

2 基于动态误差溯源理论的仿真分析

2.1 信号的分解与重构

现有一动态测试系统，其结构如图1所示，系统的各模块传递函数分别为二阶环节、增益环节、线性环节、周期环节，具体函数为

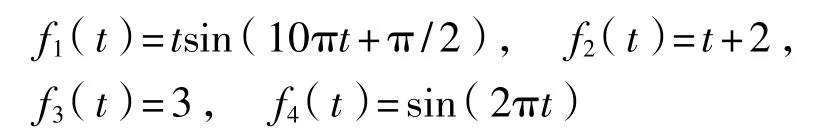
各个模块产生的误差为

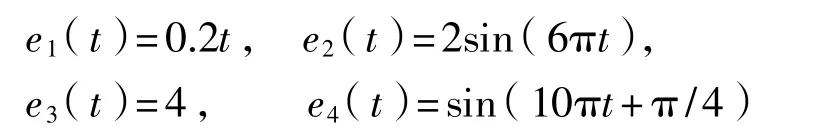
假设系统未受到外界干扰噪声影响，即nx（t）=0，ny（t）=0，根据全系统动态精度理论，系统输出总误差为

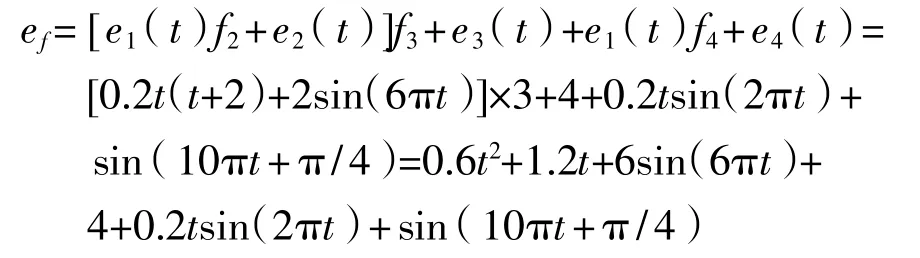
以20Hz的频率对误差信号进行采样，其结果如图3所示。

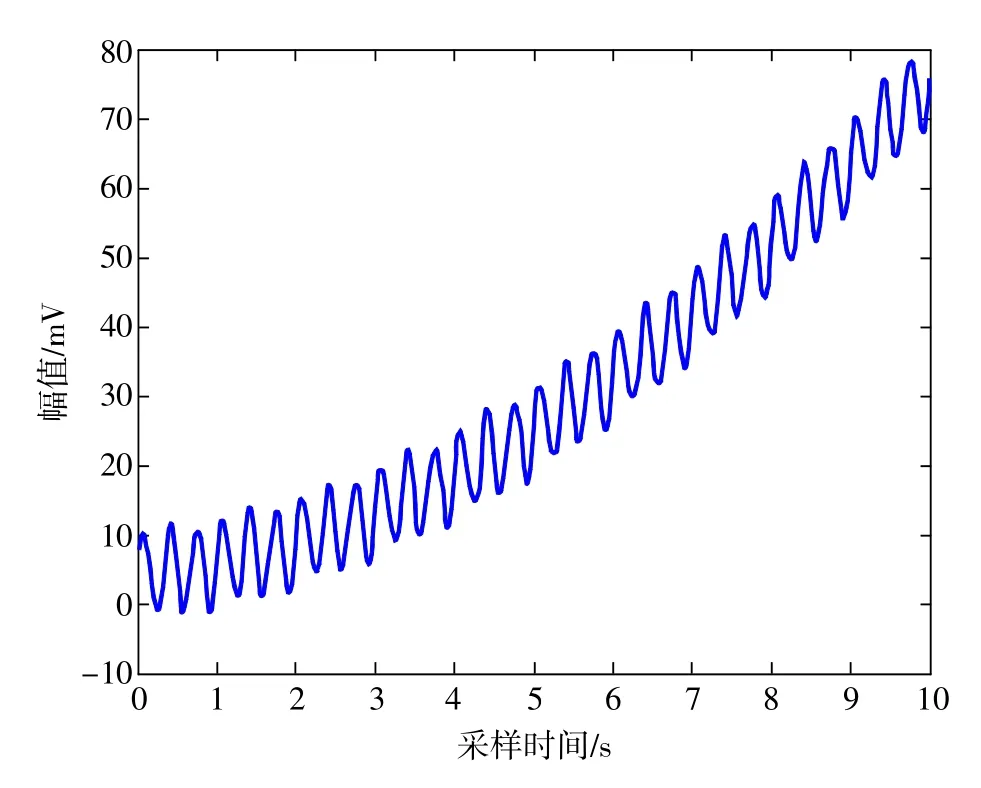
图3 原始信号

对图3进行分析，可以明显地看到原信号中包含一、二次项信号，现用最小二乘法对其进行拟合，应用Matlab中的回归拟合函数polyfit来确定其参数[8]。分解所得结果为

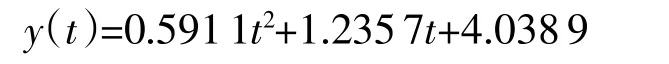
将原信号中的二次项信号去除，并对所得的信号s（t）进行小波分解，分解的结果如图4所示。

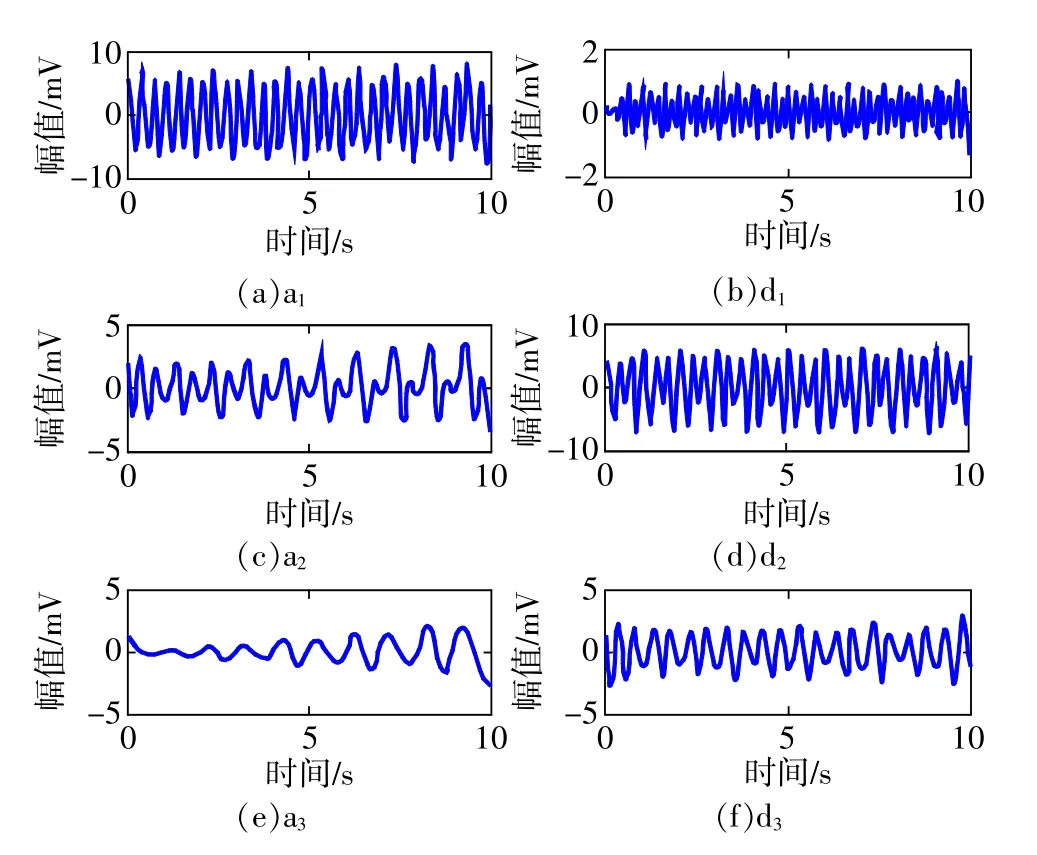
图4 小波分解的结果

由图4（e）可以看出，该信号为一频率为1Hz的信号，将图4（b）放大后，与（e）进行比较，两者的频率比为5∶1；同样，图4（d）与（e）的频率比为3∶1。所以，s（t）中包含频率分别为1，3，5Hz的周期信号。但是在图4中，周期信号的幅值不明确，进一步对信号进行分析，确定其各个信号幅值大小。此时采用线性神经网络来分解信号。首先，以sin（6πt）和cos（6πt）作为输入，s（t）作为输出训练神经网络，得出权值和阈值，则分解出的信号s1（t）=5.9947sin（6πt）；其次，以sin（10πt）和cos（10πt）作为输入，s（t）-s1（t）作为输出训练神经网络，得出权值和阈值，则分解出的信号s2（t）=0.7131cos（10πt）+0.704 4sin（10πt），可另表示为s2（t）=1.002sin（10πt+π/4）；最后，由图4（e）可分析发现，频率为1Hz的信号是一幅值随时间增大的信号，则现在以tsin（2πt）和tcos（2πt）作为输入，s（t）-s1（t）-s2（t）作为输出训练神经网络，得出权值和阈值，则分解出的信号为s3（t）=0.1961tsin（2πt）。根据上述分析，重构系统输出总误差为

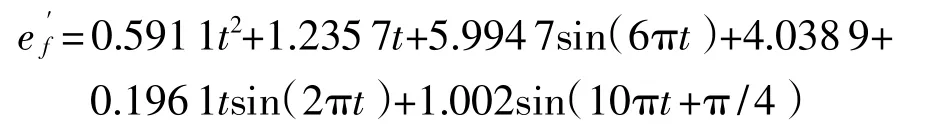
则原误差信号与重构误差信号如图5所示。

由图5可知，重构误差与原误差基本吻合，表明该分解方法具有可行性。

2.2 基于PSO的误差溯源

根据动态测试系统的结构及传递链函数[9-11]，结合重构的系统输出总误差，可以得出模块1的误差e10=0.196 1t，模块2的误差e20范围为[-3，11]，模块3的误差e30范围为[-3，11]，模块4的误差e40范围为[-3，11]。设种群粒子数为20，粒子Xi=（Xi1，Xi2，Xi3），i=1，2，…，20，若已知模块3产生的误差为一常量，则Xi1，Xi3初始值设置为误差范围内的随机数，Xi2初始值设置为4.0389，迭代次数为200次。适应度fit-以50Hz的频率取0～4s的动态误差作为样本数据，运用式（2）～式（4）进行误差溯源。因为一次计算随机性较大，本文将5次计算结果取平均值作为最后的输出结果，其结果如图6所示。

图5 原误差与重构误差对比

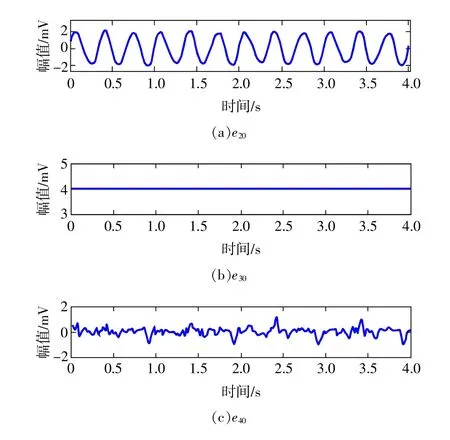
图6 PSO误差溯源结果

可以看出，e20是一频率为3Hz，幅值为2 mV的近似周期信号，因此可以得出e20=1.998sin（6πt），e30为一常量，e40特征不明显，但可以通过重构误差信号和其他误差分量得出其值，所以：

由设定的条件可知，经过误差溯源所得的各个模块产生的误差与原误差基本相符，偏差准确度为0.01，满足误差溯源的要求。可以认为这种方法能够有效地找到误差源，具有可实现性。

3 结束语

本文在动态精度理论基础上，提出了运用小波神经网络和PSO算法相结合的方法对动态误差进行溯源，通过仿真发现该方法可以快速有效地追溯到误差产生的源头，且偏差准确度在10-2，这对于动态误差的研究具有一定的应用价值。

随着动态精度理论的不断发展，误差溯源的理论也会更加完善。本文提出的方法能够在一定程度上解决误差溯源的问题，但在非理想环境下精度仍达不到理论要求，有待于进一步研究。

[1]许祯英，费业泰，陈晓怀.动态精度理论研究与发展[J].仪器仪表学报，2001（s2）：70-71.

[2]许桢英.动态测量系统误差溯源与精度损失诊断的理论与方法研究[D].合肥：合肥工业大学，2004.

[3]李晓惠.动态测量误差分解及溯源研究[D].合肥：合肥工业大学，2006.

[4]李晓惠，陈晓怀，卫兵.基于神经网络的动态测量误差分解研究[J].工业计量，2005（6）：6-9.

[5]成礼智.小波的理论与应用[M].北京：科学出版社，2004：150-157.

[6]Mix D F.小波基础及应用教程[M].北京：机械工业出版社，2006：35-61.

[7]马强，许帧英.动态测量误差溯源方法研究[J].安徽机电学院学报，2001，16（4）：22-25.

[8]史峰，王辉，郁磊，等.Matlab智能算法30个案例分析[M].北京：北京航空航天大学出版社，2011：203-205.

[9]李明爱，马建勇，杨金福.基于小波包和熵准则的最优频段提取方法[J].仪器仪表学报，2012，33（8）：1721-1728.

[10]姜焰鸣，刘桂雄.平面度误差粒子群算法评定的不确定度评估[J].中国测试，2013，39（1）：13-16.

[11]谢永成，贺芳君，李光升.基于改进型小波神经网络的灭火系统故障诊断[J].电子测量技术，2012，35（4）：128-131.

Research of dynamic error tracing method based on wavelet neural network and PSO

WU Xiao-min，LI Shi-ping，CHENG Shuang-jiang
（The Second Artillery Engineering University，Xi’an 710025，China）

With wavelet neural network and particle swarm optimization，a method of dynamic error tracing was presented to solve the accuracy loss in dynamic testing system.Firstly，wavelet neural network was carried out to decompose the output error of dynamic testing system according to the theory ofwhole system dynamic precision.With the resultofdecomposing， particle swarm optimization was used to seek errorsources.The simulation results show thatthe method accomplishes dynamic error tracing effectively and tracing accuracy reaches 10-2.

dynamic error tracing；wavelet neural network；PSO；dynamic testing system

TP183；TN911.7；TP277；TM930.115

：A

：1674-5124（2014)06-0027-04

10.11857/j.issn.1674-5124.2014.06.007

2014-01-25；

：2014-03-22

邬肖敏（1990-），男，江苏如东县人，硕士研究生，专业方向为控制科学与工程。