RC偏压构件精细抗力概率模型

蒋友宝，廖 强，冯 鹏

（长沙理工大学 土木与建筑学院，长沙 410004）

中国现行标准［1］在校核RC偏压构件截面的可靠度时，是按固定偏心距的思路来分析的，即按某一固定偏心距值来选择对应的抗力统计参数。这是一种不考虑偏压破坏模式随机不确定性的思路，因而当偏压破坏模式会随机变化时，按这种思路得到的可靠度校核结果将会有一定的误差。

贡金鑫等［2］的研究表明，即使不考虑偏心距的随机变异性，设计为大偏压的构件仍会有发生小偏压破坏的可能；而设计为小偏压的构件也会有发生大偏压破坏的可能，即偏压破坏模式的随机可变性是较为常见的。实际结构中由于荷载的非完全相关性［3－4］，构件截面上的弯矩和轴压力亦是非完全相关的，即偏心距具有较强的随机变异特性，显然此时这种偏压破坏模式的随机可变性将会增强。而现行标准［1］中的可靠度分析方法因对此考虑不够充分将会高估大偏压构件的设计可靠指标［5－7］，使得设计偏于不安全。研究表明RC大偏压柱设计偏于不安全的问题亦存在于多个国家的结构设计规范中。例如Milner等［8］的分析表明轴压力与弯矩的随机相关性（即偏心距的随机特性）对RC柱可靠度的影响较大，当轴压力低于界限轴压力时（即大偏压情形），按美国ACI-318规范设计的RC柱会偏于不安全。另外，Hong等［9］分析了按加拿大规范设计的RC柱可靠度，结果表明不考虑偏心距的随机特性会使RC大偏压柱的设计可靠度偏低目标可靠度较多。由于极限状态时，RC偏压构件截面能承受的轴压力和弯矩是一条复杂的相关曲线，因此相关研究多采用数值积分 方 法［8－9］或 Monte Carlo方 法［10－11］等 来 计 算可靠度。事实上若能获得一个随偏心距值连续变化的抗力概率模型，则在偏心距和荷载效应的随机概率分布已知的情形下，可采用成熟的JC算法来求得不同偏心距值下的条件失效概率，然后由全概率原理便能较为精确地求得失效概率值。因此在这种思路下，如何获得随偏心距值连续变化的抗力概率模型便较为关键。Mirza等［12］采用Monte Carlo方法分析了美国ACI规范中RC偏压构件在不同偏心距和配筋率下的抗力概率模型，然后应用这些概率模型，基于可靠度校准得到了美国规范用抗力分项系数值。对比之下，中国现行标准［1］中偏压构件抗力统计参数却较为粗糙，仅以两种偏压（大小偏压）状态之分来给出相应的抗力统计参数，因而当偏心距值变化、配筋率变化时，标准［1］中的抗力统计参数将较难精确地反映这种变化。这给RC偏压构件的可靠度分析与设计带来了一定程度的不精确性。

本文研究了不同偏心距和配筋率下RC偏压构件的抗力统计参数。在此基础上，对比分析了随机偏心距下不同RC偏压构件抗力概率模型的适用性，供相关人员参考。

1 RC偏压构件抗力模型的分析方法

1.1 不同偏心距下抗力的计算

考虑柱截面为对称配筋的情形，依据现行混凝土结构设计规范［13］，当柱截面在偏心距e下达到极限状态时，相应的承载力计算式为

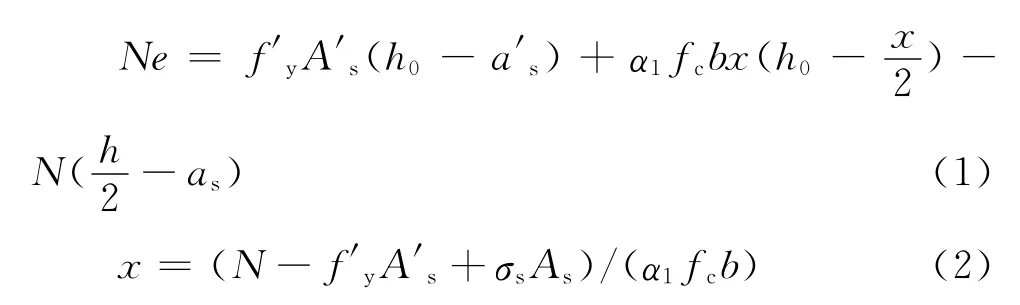
式中：f′y为钢筋抗压强度；A′s为受压钢筋面积；fc为混凝土抗压强度；α1为等效矩形受压区的应力换算系数（C50以下取为1.0）；x为等效矩形受压区的高度；h和h0分别为截面的几何高度和有效高度；b为截面宽度；a′s和as分别为两侧钢筋重心至相应边缘的距离；σs和As分别为远离轴向压力一侧的钢筋应力和面积。

对于大偏压破坏的情形，远离轴向压力一侧的钢筋受拉能够屈服，即σs＝fy，这样可求得此时柱截面所能承受的轴向压力值N u，其计算式为

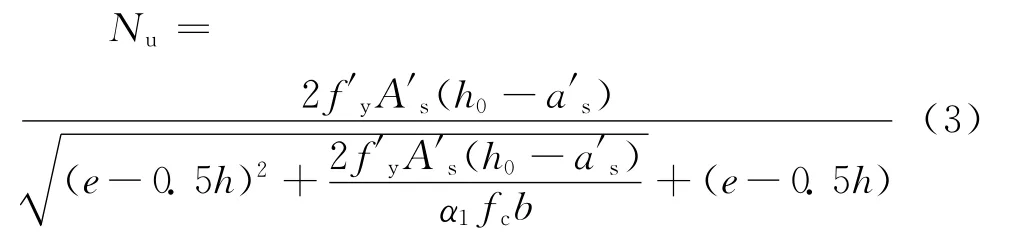
而对于小偏压破坏的情形，远离轴向压力一侧的钢筋受拉不能屈服，σs可按式（4）计算。

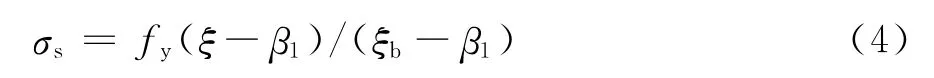
式中：ξ为相对受压区高度；ξb为相对界限受压区高度，取为0.55；β1为等效矩形应力图形中引入的高度系数，取为0.8。设此时柱截面所能承受的轴向压力值为Nu，其计算式为

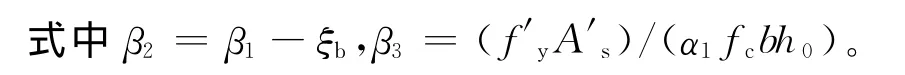
1.2 现行规范抗力概率模型的说明

现行标准［1］中偏压构件抗力模型中的统计参数如表1所示，其中κ表示平均值与标准值之比值，δ为变异系数。由于轴心受压构件与受弯构件可视为偏压构件中偏心距e＝0和e＝∞的特例，因此表1同时列出了这两类构件的统计参数。

表1 各种构件的抗力统计参数

从表1可知，小偏压构件抗力模型中κ与δ值均较大；而大偏压构件抗力模型中κ与δ值均较小；且表1中不同偏心受力情形下κ与δ值的变化程度较大，例如当e＝0变化至e＝∞时，κ值下降了15%，δ值下降了41%。这说明现行标准中偏压构件抗力统计参数较为粗糙，没有给出不同偏心距值下的抗力统计参数，因此需加以完善。

1.3 不同偏心距下抗力概率模型的分析方法

由于抗力不确定的因素主要有材料强度的不确定性、截面几何参数的不确定性和计算模式的不确定性。对于RC偏压构件，参考文献［14］，各种不确定变量的统计参数如表2所示。

表2 各种抗力因素的统计参数

由式（3）、式（5）可知偏压构件的抗力是混凝土强度、钢筋强度和截面几何参数的复杂函数，再考虑计算模式不确定性后此函数式将更为复杂，因此应用解析方法来推导其统计参数较为困难，为此采用Monte Carlo方法来进行分析。定义归一化的抗力变量R′，其计算式为

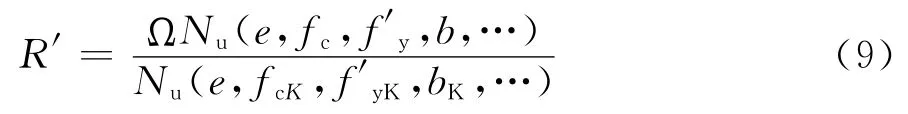
式中Ω为计算模式不定性变量，下标K表示标准值。相应的计算流程如图1所示。Mirza等［12］亦采用相同的思路对美国ACI规范中RC偏压构件的抗力概率模型进行了分析。可见，这种获得抗力概率模型的分析方法具有较好的适用性和精度。

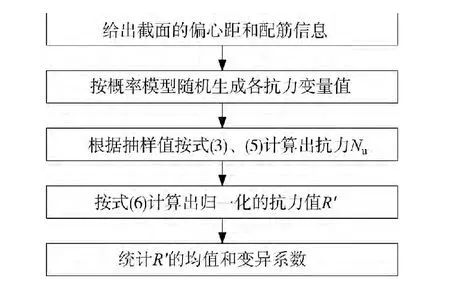
图1 抗力抽样计算流程图

2 抗力概率模型的参数分析

2.1 偏心距和配筋率的影响分析

由式（1）、（2）可求得RC偏压构件界限破坏状态时，对应的偏心距值eb为

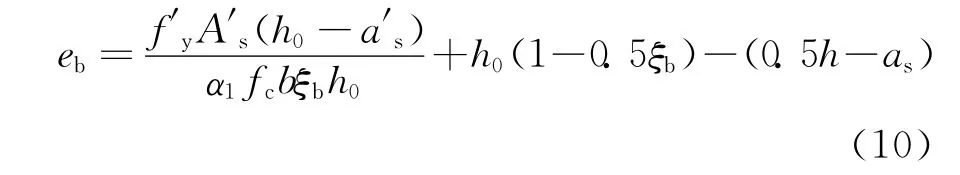
当截面对称配筋时有ρs＝A′s／bh0。近似假定h0＝0.9h和a′s＝0.1h，则当ρs在0.5%～2.0%内取值时，可求得eb的取值范围为0.37h至0.74h（钢筋和混凝土强度暂按标准值考虑）。

在各种抗力因素的统计参数给定时，由式（3）、（5）可知偏压构件抗力模型中的κ与δ值还与偏心距e、配筋率ρs有关。考虑偏心距在0.05～5h范围内变化，配筋率在0.5%～2.0%范围内变化，此时不同偏心距与配筋率下偏压构件抗力模型中的κ与δ值分别如图2、图3所示。

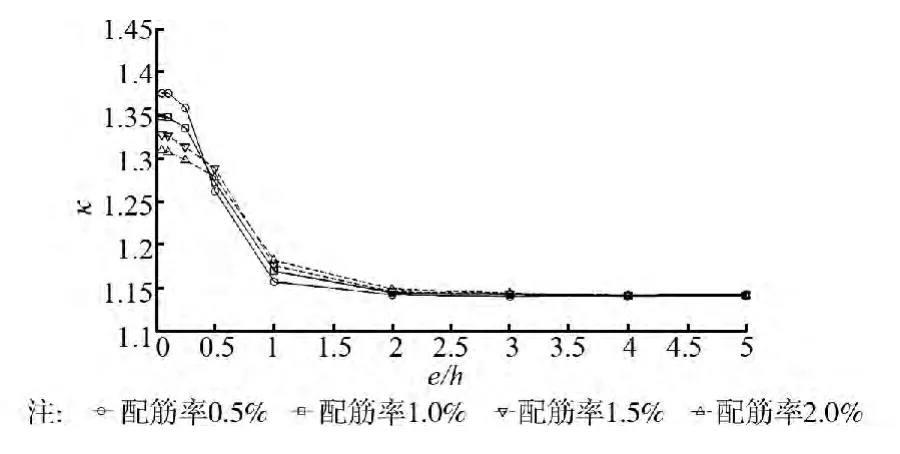
图2 κ值随偏心距与配筋率的变化曲线

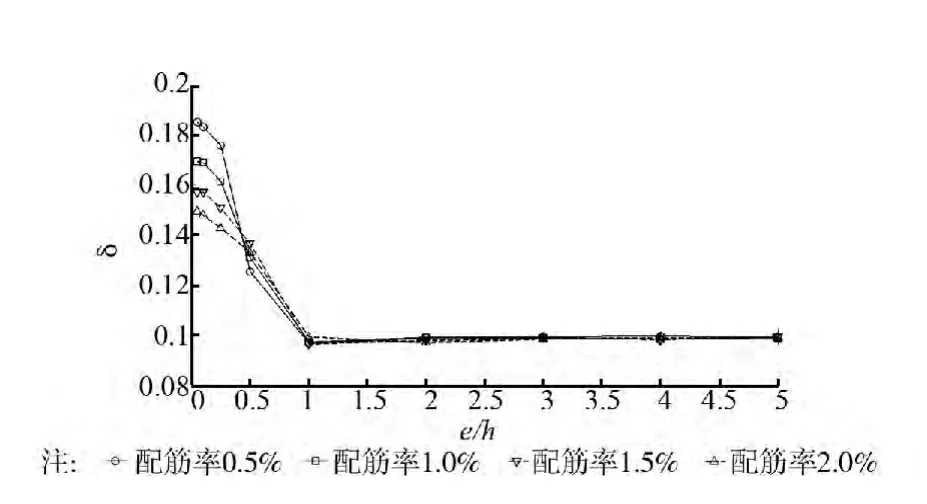
图3 δ值随偏心距与配筋率的变化曲线

计算表明，当偏心距较小（e≤0.25h）时，随配筋率的增大，κ与δ值均减小。当e＝0.05h时，不同配筋率下κ值的变化范围为1.31～1.38，δ值的变化范围为0.15～0.185，这些数值与表1中轴心受压构件的抗力统计参数较为接近。而当偏心距较大（e≥0.5h）时，配筋率的变化对κ与δ值的影响开始减小，尤其是当e≥2.0h时，κ值已较为稳定，约为1.14；δ值亦较为稳定，约为0.10，这些数值与表1中受弯构件的抗力统计参数非常接近。

这说明采用Monte Carlo方法计算得到的抗力统计参数在偏压构件接近轴心受压或受弯状态时与现行标准给出的抗力统计参数是一致的，同时也说明计算方法具有较好的精度。

2.2 抗力的概率分布模型

结构可靠度分析时，抗力一般假定服从正态或对数正态分布。当ρs为1.0%时，典型情形下的抗力概率分布见图4。

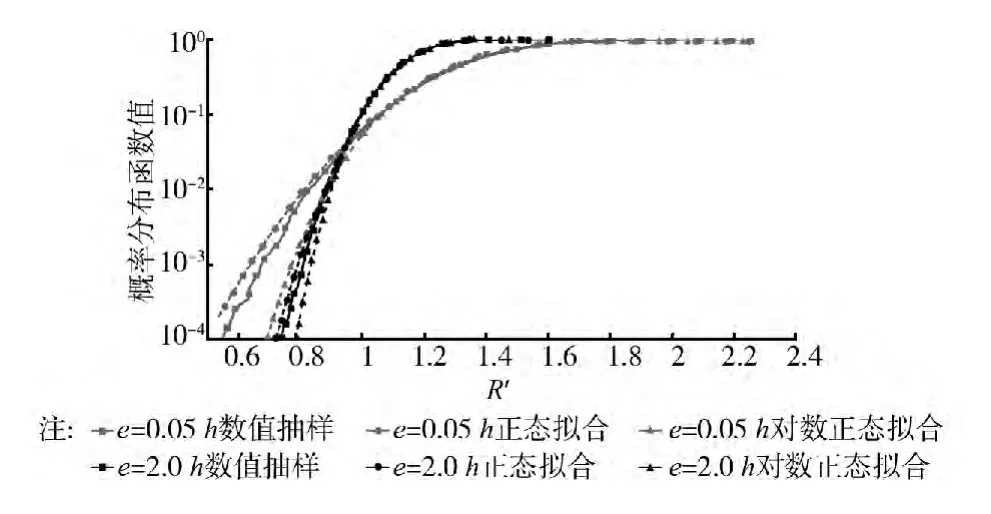
图4 不同抗力概率分布模型的对比

从图4中可看出，对于大偏压构件，正态或对数正态分布均具有较好的拟合精度；但对于小偏压构件，正态分布的拟合精度要优于对数正态分布的拟合精度。当配筋率和偏心距值取其他参数时，仍有此结论。因此综合考虑，可认为RC偏压构件的抗力服从正态分布。

对多种情形下的抗力统计参数进行数值分析可知，不同偏心距和配筋率下κ与δ值均可用式（11）所示的函数模型来拟合。

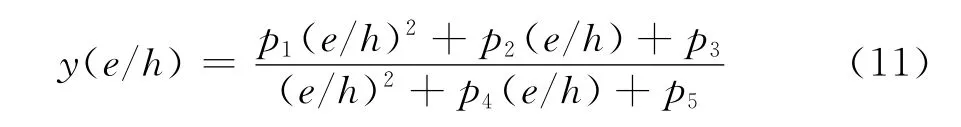
式中p1、p2、p3、p4和p5均为与配筋率有关的拟合参数。其中p1表示e／h为∞（受弯）时的κ或δ值，p3／p5表示e／h为0（轴心受压）时的κ或δ值，其余拟合参数为反映κ或δ随e／h变化曲线特征的参数。当偏心距在0.05～2.0h内取值时，不同配筋率下的拟合参数值见表3、表4。

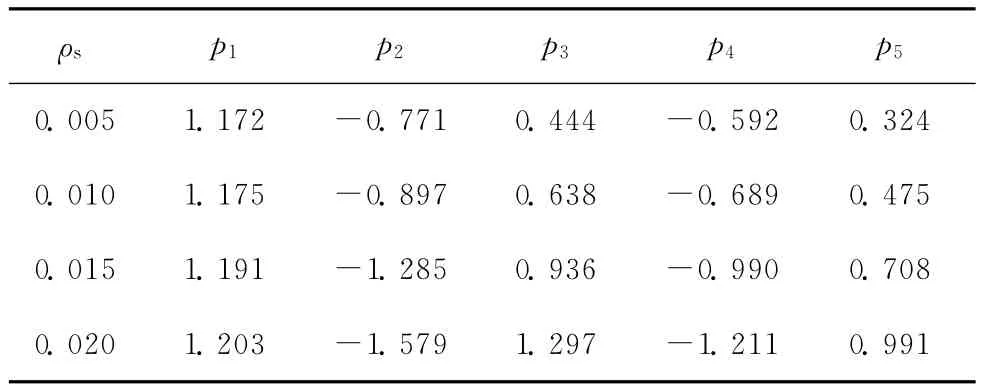
表3 不同配筋率下与κ值有关的拟合参数值

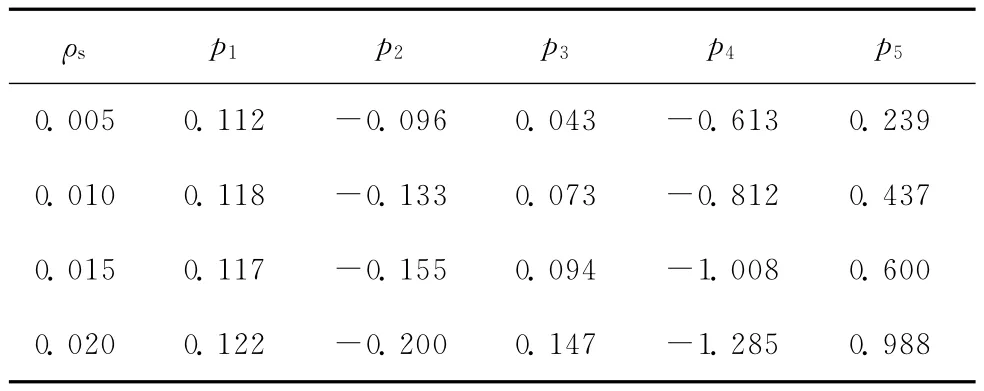
表4 不同配筋率下与δ值有关的拟合参数值

依据表3、表4中拟合参数计算得到统计参数值与直接采用Monte Carlo方法得到的数值非常接近，最大误差不超过4%。当配筋率取其他中间值时，抗力模型的κ和δ值可近似由表3、表4插值得到。而当偏心距e≥2.0h时，由2.1节知，κ值可直接取为1.14，δ值可取为0.10。

3 随机偏心距下的适用性分析

3.1 随机偏心距下抗力的换算

根据式（9）计算的抗力统计参数是在给定偏心距值下抗力变量按其概率模型随机抽样来得到的，这与随机偏心距下的实际设计情形有一定出入。实际设计时一般仅用偏心距设计值ed下的抗力统计参数来衡量，并不用其他随机偏心距值所对应的抗力统计参数。为此引入一换算系数λ，其计算式为

式（12）中e的取值范围可考虑为0.75ed～1.75ed，因为在此范围内偏心距随机取值对可靠度有较大影响。当各抗力变量随机变化时，λ值也会随机波动。由于抗力函数较为复杂，此处仍采用Monte Carlo方法来获得λ的统计特性。

计算表明，当配筋率在0.5%～2.0%内变化时，ed在0.05～4.0h内变化时，λ的变异系数值较小，多数情形下不超过0.04，因此为简化分析，可将λ按一确定的变量考虑，用其均值来代表。而在同样的参数变化范围内，λ均值变化较大，例如当配筋率为1.0%时，λ均值如表5所示，其他配筋率下λ均值与此相似。

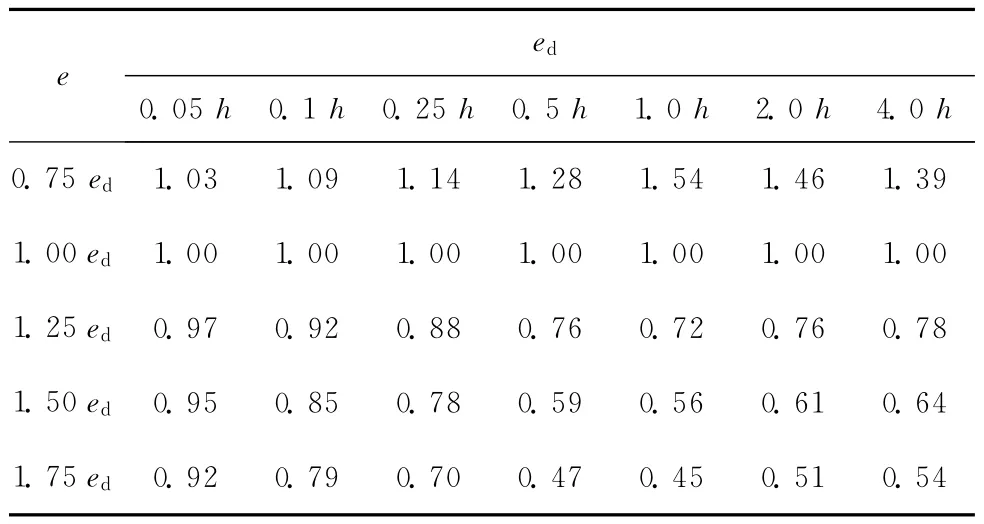
表5 配筋率为1.0%时λ的均值

当偏心距存在随机变异性时，可将偏心距的概率分布曲线离散成n个区段，设τ为离散步长，取每个区段的中点值ei作为该区段偏心距的代表值，因此由全概率计算公式可求得失效概率为

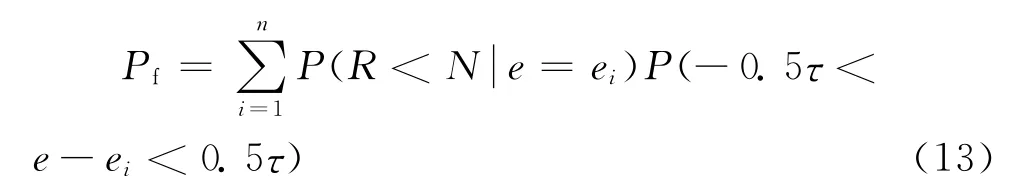
式中右边第一项表示给定偏心距值ei时的条件失效概率；第二项表示偏心距在 ［ei－0.5τ，ei＋0.5τ］内的分布概率。将λ代入式（13）中右边第一项，可得到对应的极限状态方程

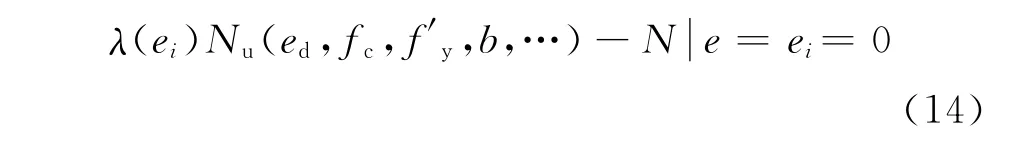
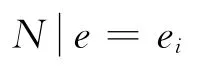
3.2 不同抗力概率模型的适用性分析

从表5中可知，若偏心距设计值较大（e≥0.5h）时，则偏心距取某一大于偏心距设计值的随机值时，λ值会小于1.0较多，这显然会增大式（14）失效的可能。这表明当偏心距设计值较大时，对失效概率贡献较大的是偏心距取值大于偏心距设计值的情形。而现行设计方法在校核偏压构件可靠度时是按固定偏心距思路来确定抗力代表值，进而选定其抗力概率模型。显然这种思路对抗力随偏心距值增大而减小的效应考虑不够充分，因此偏于不安全。

另外当偏心距设计值取为界限偏心距附近的数值时，将会导致设计为小偏压状态，却出现大偏压失效占较大可能的情形。此时由于现行标准中大小偏压状态对应的抗力统计参数有较大的差异，因而按现行标准中相应的抗力统计参数来计算可靠度将会有较大的误差。

而本文建议的抗力概率模型由于考虑了随偏心距的变化，因而能更好地适用于随机偏心距的情形，文后的算例分析会证明这点。此外该抗力概率模型还考虑了随配筋率的变化，因而其适用性较现行标准中的抗力概率模型会更好一些。

4 算例验证

4.1 算例1（大偏压构件的可靠度分析）

设一RC偏压构件，其轴压力设计值Nd为532 k N，偏心距设计值ed＝0.308 m。假定偏心距的概率分布值、不同偏心距下的轴压力统计参数如表6所示，其中偏心距概率分布曲线的离散长度为0.1ed，每个区段的代表值为中点值ei，F（ei）表示偏心距在［ei－0.05ed，ei＋0.05ed］内的分布概率值。

若该构件采用300 mm×400 mm矩形对称配筋截面，混凝土强度等级为C30，单侧配有截面积为942 mm2的HRB335级别钢筋。按现行规范验算，该构件为大偏压构件，且恰能满足设计要求。

表6 算例1中偏心距与轴压力的统计参数

若不考虑偏心距随机特性，按式（3）可求得抗力标准值为630 k N。假定抗力和轴压力均服从正态分布，参见表1中大偏压构件的抗力统计参数及表6中ei＝ed时的荷载统计参数可求得可靠指标为2.77。

若考虑偏心距的随机特性，则在关注的ei区域内，按式（11）可计算出不同偏心距值下抗力模型中的κ与δ值，再由Monte Carlo方法统计得到λ值，最终根据全概率公式（13）来计算总的失效概率。具体计算过程见表7，可求得失效概率为0.009 4，对应可靠指标为2.35。由表7可知，对失效概率贡献较大的是偏心距随机取 ［1.25ed，1.55ed］区间内值时的条件失效概率，此区间中点值对应的λ值平均约为0.594，抗力下降程度较多。

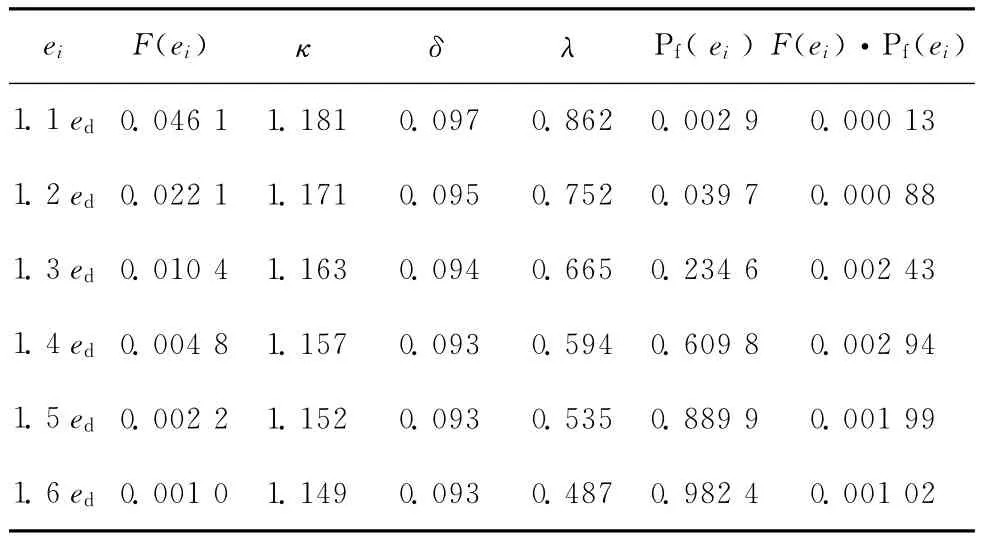
表7 按建议抗力概率模型计算得到的失效概率

若在表7中，不同ei值下均采用表1中大偏压构件的κ和δ值，计算得到的可靠指标值为2.26。而若采用Monte Carlo方法直接进行抽样，得到的失效概率值分别为0.009，对应可靠指标2.37。对于此算例，各种情形下可靠指标的对比见表8。

表8 不同计算模式下大偏压构件可靠指标

可见，不考虑偏心距的随机特性，按现行标准中大偏压构件抗力模型进行计算将会高估其可靠度较多，偏于不安全。而考虑偏心距随机特性后，按现行标准中大偏压构件抗力模型得到的可靠度又会偏低

（对应失效概率偏高34%）。相比之下，建议的抗力概率模型的计算精度要更好一些。

4.2 算例2（临近界限时偏压构件的可靠度分析）

在算例1中，若设计轴压力Nd为873 k N（界限轴压力为849 k N），偏心距设计值为ed＝0.2 m，偏心距的概率分布值、不同偏心距下的轴压力统计参数如表9所示，且假定仍采用相同的配筋截面，可知按小偏压构件验算也恰能满足要求。

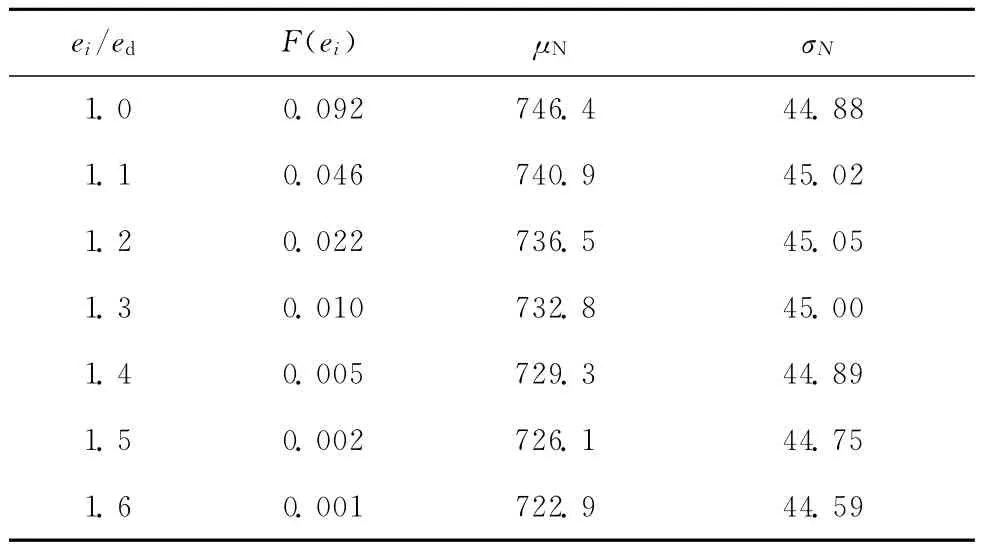
表9 算例2中偏心距与轴压力的统计参数

若不考虑偏心距的随机特性，按式（5）可求得抗力标准值为1 104 k N，这样参见表1中小偏压构件的抗力统计参数及表9中ei＝ed时的荷载统计参数可求得可靠指标为3.13。

算例采用Monte Carlo方法直接进行抽样得到的可靠指标为2.78，且抽样结果表明大部分失效样本点发生的并不是设计时的小偏压破坏情形，而是大偏压破坏情形。考虑偏心距的随机特性后，采用本文建议的抗力概率模型，可求得可靠指标为2.77；而不同ei值下若均采用表1中大偏压构件的抗力统计参数可求得可靠指标为2.53。各种情形下可靠指标的对比见表10。

表10 不同计算模式下临近界限偏压构件可靠指标

可见，不考虑偏心距随机特性时，按现行标准中小偏压构件抗力概率模型计算得到可靠指标偏高0.35（对应失效概率偏低68%）；而考虑偏心距的随机特性后，按现行标准中大偏压构件抗力概率模型来计算得到的可靠度则又偏低（对应失效概率偏高110%）。因此，无论采用现行标准中的何种抗力概率模型，可靠度计算结果均有较大的误差。而本文建议的抗力概率模型仍然具有较好的精度。

5 结 论

采用Monte Carlo方法研究了不同偏心距和配筋率下RC偏压构件的抗力概率模型，改进了现有抗力概率模型较为粗糙、且在随机偏心距情形下适用性较差的不足。主要研究结论如下：

1）当偏心距具有随机变异性时，现行大偏压构件设计方法偏于不安全的原因主要是对抗力随偏心距值增大而减小的效应考虑不够充分。

2）对于RC大偏压或小偏压构件，采用正态分布变量来拟合其抗力的概率分布具有较好的精度，优于对数正态分布变量的拟合精度。

3）当偏心距设计值接近或者大于界限偏心距值时，无论采用现行标准中的何种抗力概率模型来计算可靠度均会有较大的误差，而采用文中建议的抗力概率模型则具有较高的精度。

［1］GB 50068－2001建筑结构可靠度设计统一标准［S］.北京：中国建筑工业出版社，2001.

［2］贡金鑫，郑峤.钢筋混凝土偏心受压构件安全性的概率分析［J］.工业建筑，2003，33（11）：28-31.

Gong J X，Zheng J.Reliability analysis of reinforced concrete elements subjected to eccentric compression［J］.Industrial Construction，2003，33（11）：28-31.

［3］范文亮，李杰.非完全相关荷载下钢筋混凝土框架结构体系可靠度分析［J］.计算力学学报，2009，26（5）：620-626.

Fan W L，Li J.System reliability analysis of RC frame with non-perfect correlated loads［J］.Chinese Journal of Computational Mechanics，2009，26（5）：620-626.

［4］Leite L，Bonet J L，Pallarés L，et al.Experimental research on high strength concrete slender columns subjected to compression and uniaxial bending with unequal eccentricities at the ends ［J］.Engineering Structures，2013，48：220-232.

［5］蒋友宝，杨毅，杨伟军.基于弯矩和轴力随机相关特性的RC偏压构件可靠度分析［J］.建筑结构学报，2011，32（8）：106-112.

Jiang Y B，Yang Y，Yang W J.Reliability analysis based on random correlative characteristics between moment and axial force for RC member subjected to eccentric compression［J］.Journal of Building Structures，2011，32（8）：106-112.

［6］蒋友宝，杨伟军.基于偏心距随机特性的RC框架柱承载力抗震调整系数［J］.中南大学学报：自然科学版，2012，43（7）：2796-2802.

Jiang Y B，Yang W J.Seismic adjustment coefficient of bearing capacity for RC frame columns with random characteristics of eccentricity ［J］.Journal of Central South University：Science and Technology，2012，43（7）：2796-2802.

［7］蒋友宝，杨伟军.可变荷载效应占高比重时荷载分项系数取值研究［J］.建筑结构学报，2012，33（12）：130-135.

Jiang Y B，Yang W J.Research on values of load partial factors with large ratios of variable load effects ［J］.Journal of Building Structures，2012，33（12）：130-135.

［8］Milner J D，Spacone E，Frangopol D M.New light on performance of short and slender reinforced concrete columns under random loads ［J］.Engineering Structures，2001，23（2）：147-157.

［9］Hong H P，Zhou W.Reliability evaluation of RC columns［J］.Journal of Structural Engineering，ASCE，1999，125（7）：784-790.

［10］Frangopol D M，Ide Y，Spacone E，et al.A new look at reliability of reinforced concrete columns［J］.Structural Safety，1996，18（2／3）：123-150.

［11］黄炎生，宋欢艺，蔡健.钢筋混凝土偏心受压构件增大截面加固后可靠度分析［J］.工程力学，2010，27（8）：146-151.

Huang Y S，Song H Y，Cai J.Reliability analysis of reinforced concrete members strengthening by augmented section under eccentric compression ［J］.Engineering Mechanics，2010，27（8）：146-151.

［12］Mirza S A.Reliability-based design of reinforced concrete columns［J］.Structural Safety，1996，18（2／3）：179-194.

［13］GB 50010－2010混凝土结构设计规范［S］.北京：中国建筑工业出版社，2010.

［14］张新培.建筑结构可靠度分析与设计［M］.北京：科学出版社，2001.

［15］Jiang Y B，Yang W J.An approach based on theorem of total probability for reliability analysis of RC columns with random eccentricity［J］.Structural Safety，2013，41（1）：37-46.

（编辑王秀玲）