某型两栖装甲车作战效能评估模型

刘芬良，罗 权，李泽恩

（海军陆战学院，广州 510430）

某型两栖装甲车作战效能评估模型

刘芬良，罗 权，李泽恩

（海军陆战学院，广州 510430）

以某型两栖装甲车基本作战效能分析为基础，针对实战背景下战场环境的特点，在单车作战效能评估基础上，通过引入战场环境指数和战场生存能力指数，提出改进的ADC模型，并综合运用层次分析法和幂指数法等方法对相应子模型参数进行量化，采用定性分析与定量分析相结合的方法，实现对某型两栖装甲车作战效能的评估。并通过实例证明所建立模型的有效性，具有很强的针对性和指导性。

两栖装甲车辆，改进ADC，幂指数法，层次分析法

引 言

ADC方法是美国工业界武器系统效能咨询委员会（WSEIAC）提出的面向武器系统效能进行评估的方法。某型两栖装甲车的作战效能是指整车系统在作战条件下，完成一定作战任务要求程度的量度，是某型两栖装甲车系统的可用性（A）、可信性（D）、作战能力（C）的函数［2］。基于理想状态武器系统的理论分析方法，针对两栖作战战场环境特点，综合考虑对抗条件下某型两栖装甲车的作战效能，对ADC的基本模型进行改进，结合层次分析法和幂指数法对无法定量描述的能力指标进行定性评估。

1 评价指标体系

ADC的基本模型用可用度A、可信度D和作战能力C，反映武器系统状态随时间变化及其在作战使用过程中不同阶段的有效性。由于某型两栖装甲车遂行登陆作战任务时，作战环境复杂，对武器系统作战效能的影响较大；在攻防对抗条件下，某型两栖装甲车生存能力对作战效能有决定性影响。在分析模型时，需综合考虑某型两栖装甲车战、技术性能和影响作战效能的因素。分析实战条件下影响某型两栖装甲车的作战效能评估的要素，用图1表示：

图1 效能评估要素图

2 改进的 ADC模型［3，7］的建立

根据ADC的基本模型得到改进的ADC模型：

其中：ISC是某型两栖装甲车在未被敌火力毁伤的条件下的作战能力，即生存能力；IHJ是战场环境指数；A为可用度行向量；D为可信度矩阵；C为作战能力矩阵。

2.1 可用度向量（A）模型

系统的可用度是系统在执行任务开始时刻可用程度的量度，反映武器系统的使用准备程度。针对登陆作战的实际情况，由于某型两栖装甲车通信、指挥、承载和防护系统的性能对作战影响小或者通常可排除出现故障的可能，在这里只考虑火控系统和行动系统的可用度。在任务准备阶段，火控系统和行动系统都有“正常”和“故障”两种状态，所以某型两栖装甲车共有4种初始状态ai（i=1，2，3，4），如表 1：

表1 某型两栖装甲车的4种初始状态

设MTBF1为火控系统平均故障间隔时间，MTTR1为火控系统平均维修时间，λ1为火控系统的平均故障率，u1为火控系统维修率；MTBF2为行动系统的平均故障间隔时间，MTTR2为行动系统的平均维修时间，λ2为行动系统的平均故障率，u2为行动系统的维修率。假设行动与火控系统构成的整车系统完好性是串联关系，则初始状态可用度向量为A=（a1，a2，a3，a4），其中

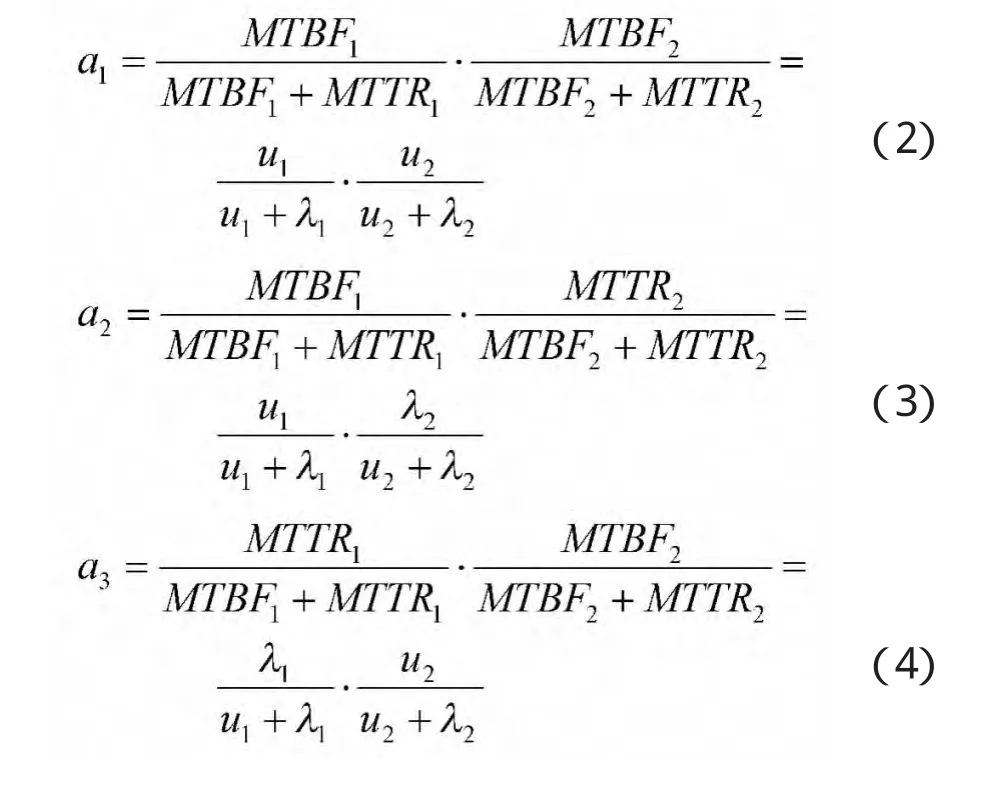
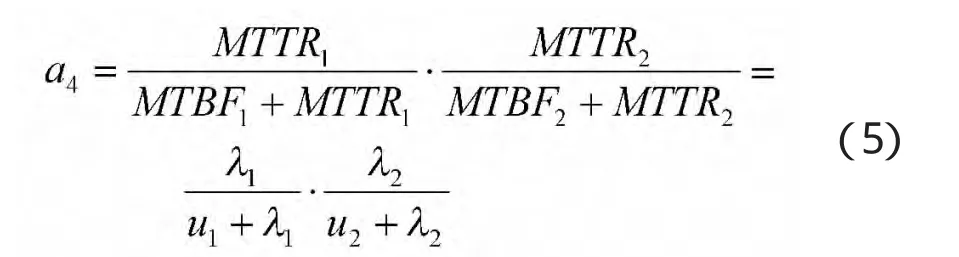
2.2 可信度矩阵（D）模型

某型两栖装甲车的可信度表示整车系统在使用过程中完成规定功能的概率。由于整车系统在执行任务时有4个可能状态，则可信度D是一个4×4矩阵（可信赖性矩阵）。假设在任务过程中故障无法维修，则无法使故障状态转换到正常状态，即可信赖性矩阵为上三角矩阵：

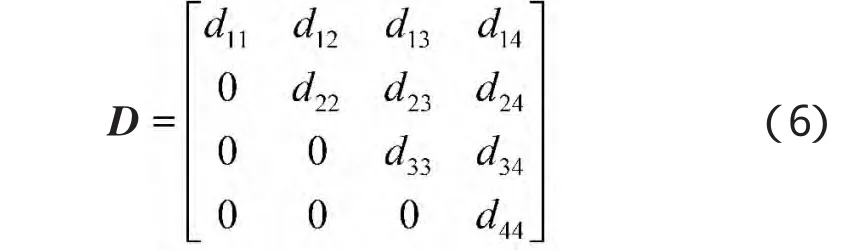
式中，dij（i=1，2，3，4；j=1，2，3，4）是使用开始时系统处于i状态而在使用过程中转移到j状态的概率。

设Xij（i=1，2；j=1，2）为行动系统从状态i到状态 j的概率，Hij（i=1，2；j=1，2） 为火控系统从状态 i到状态j的概率（状态1为正常，状态2为故障），T为执行任务时间。执行任务过程中不能修理，则u=0，且系统故障服从指数定律，可得：

2.3 作战能力矩阵（C）模型

作战能力指某型两栖装甲车在可用和可信状态下，能达到任务目标的概率，很大程度上取决于系统执行任务的最后可能状态，武器系统效能分析的关键，在于用不同的方法来建立C的计算模型。某型两栖装甲车遂行作战任务时作战能力参数是一个动态的量，与打击距离、机动状态、目标信息和射手素质等因素有关。在此主要是对单目标毁伤任务。当系统故障时，此状态下的能力值显然为0，在其余状态下，均为正常工作状态的品质因数。设定作战能力矩阵：

其中，ci（i=1，2，3，4）表示某型两栖装甲车在状态i下完成任务的概率。设整车系统发现目标的概率为pf，命中目标的概率为pm，毁伤目标的概率ph，则得：

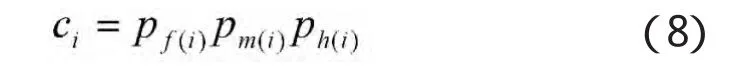
2.4 生存能力（ISC）［1］

为了计算某型两栖装甲车的战场（以登陆作战为例）生存能力，建立如图2所示的评价指标体系。

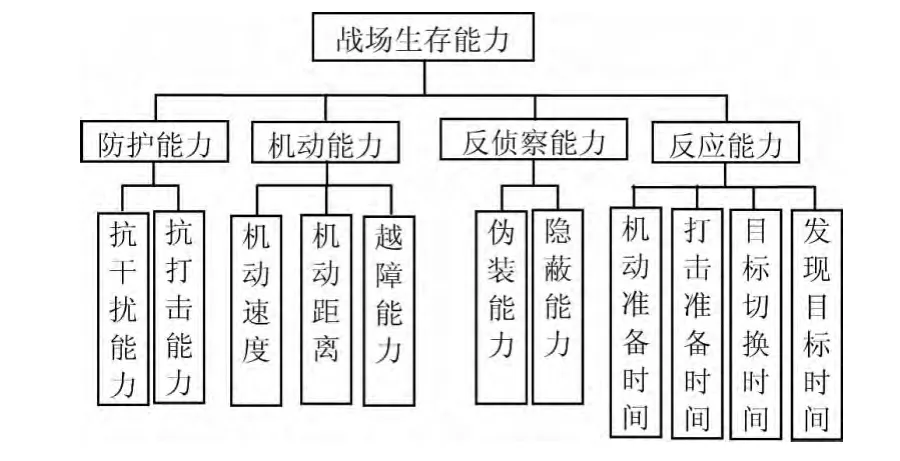
图2 战场生存能力评价体系图

影响战场生存能力的不仅有客观因素还有许多主观因素，用幂指数法［5-6］计算战场生存能力，用层次分析法确定幂指数的参数。参考文献［4］，通过专家打分，根据萨蒂对于因素两两比较时相对偏好判断的九级标度构造两两比较矩阵，用几何平均法计算矩阵，得到目标合成权重并排序［4］。计算得反坦克导弹战场生存能力模型为：

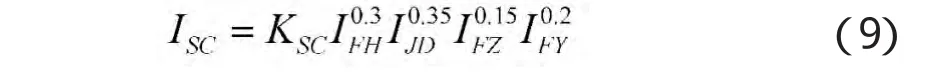
其中KSC为次指标权重系数。

同理，防护能力（FH）包含抗干扰能力（KG）和抗打击能力（KD），其模型为：

机动能力（JD）包含机动速度（SD）、机动距离（JL）和越障能力（YZ），模型为：

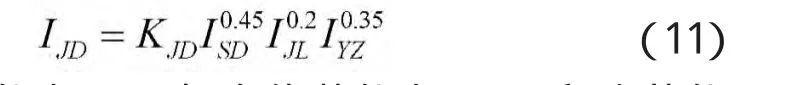
反侦察能力（FZ）包含伪装能力（WZ）和隐蔽能力（YB），模型为：

反应能力包含激动准备时间（JZ）、打击准备时间（DZ）、目标切换时间（QH）和发现目标时间（FX），模型为：

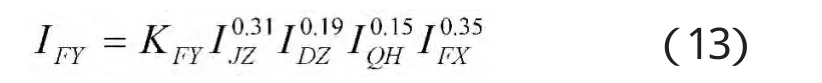
将式（10）～式（13）代入式（9）便可以得到某型两栖装甲车战场生存能力指数。

2.5战场环境指数（IHJ）［1］

根据两栖作战的战场环境特点，综合分析登陆作战中影响某型两栖装甲车的作战效能的因素，构建战场环境指数评价体系如图3：

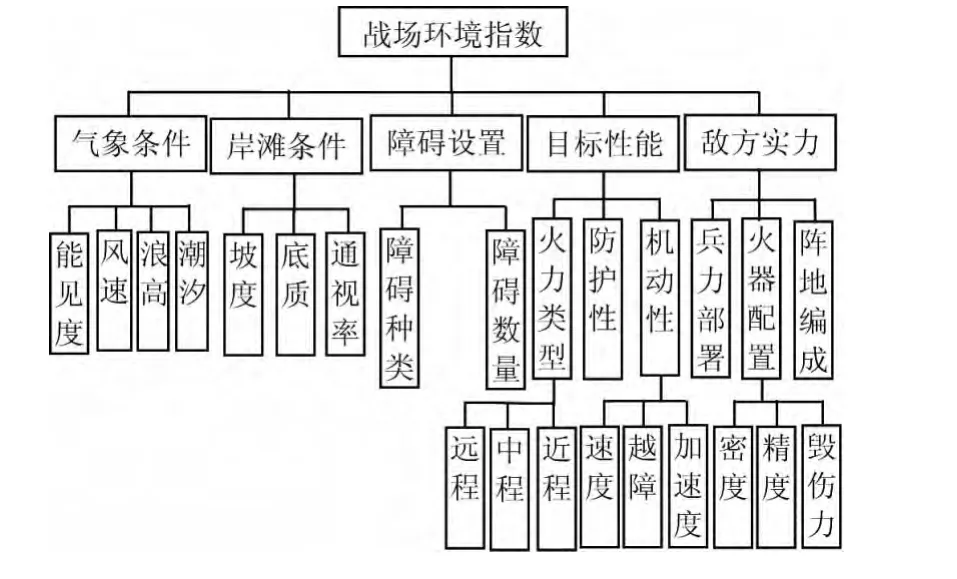
图3 战场环境指数评价体系图

由幂指数法和层次分析法可得：

KHJ为子指标权重系数，IHJ，IQX，IAT，IZA，IMB，IDF，分别表示战场环境、气象条件、岸滩条件、障碍设置、目标性能和敌方实力指数；ωi（i=1，2，3，4，5）分别为幂指数。根据所处战场环境具体情况的分析，运用层次分析法可确定幂指数的数值，在这里省略具体计算步骤。

3 实例分析

用上述评估模型对两台设定的某型两栖装甲车进行作战效能评估。设定在进行部分性能改进后，2号车的可靠性和战场生存能力比1号车有所提高，两台某型两栖装甲车参加同一次登陆作战并处于相同作战环境，每台某型两栖装甲车每次单独面对一个作战目标（敌方坦克），并处于目标射程之内（相距800m）。作战时间为2 h。各参数取值见表2、表3（表3中各指标后的数值分别为其权重）。

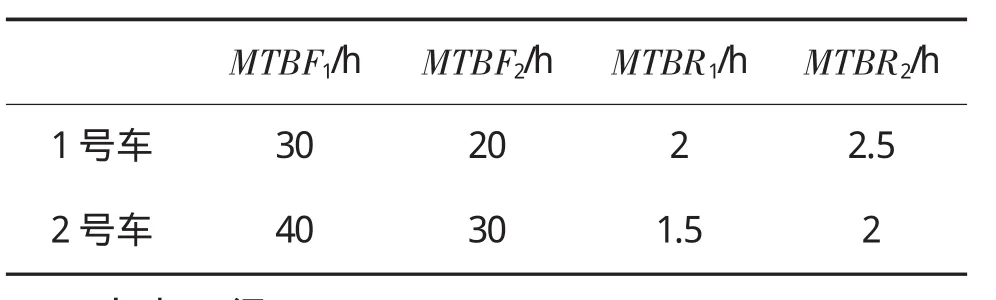
表2 可靠性参数表

由表2得：

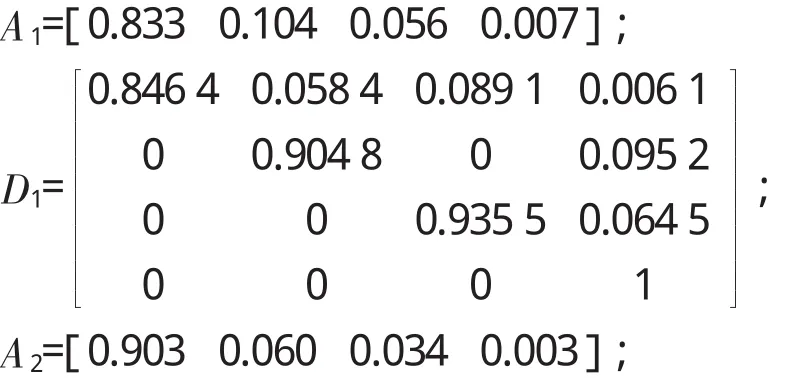
由于是同一次作战的相同作战环境，所以次指标和子指标权重系数及战场环境相同，都设为1，由表 3可得，ISC1=0.769 5，ISC2=0.831 7，最后可得到E1=0.542 5，E2=668 3。

分析计算结果，可见随着2号某型两栖装甲车可靠性提高和战场生存能力的增强，整车的作战效能明显增强。计算结果与实际相符，充分验证了采用改进ADC法评估某型两栖装甲车的作战效能的有效性。

4 结束语

该模型在某型两栖装甲车的单车作战效能评估基础上，引入了战场环境指数和战场生存能力指数，更加符合作战实际，相对于一般的武器系统作战模型有了一定程度的改进，并通过实例证明所建立模型的有效性，具有很强的针对性和指导性。

［1］伍文峰，赵 健，何 军.车载式反坦克导弹系统作战效能评估模型［J］.弹箭与制导学报，2007，27（5），87-90.

［2］王世学，李兆耿.基于改进ADC模型的坦克作战效能评估［J］.兵工自动化，2009，28（7），14-16.

［3］张最良，李长生，赵文志，等.军事运筹学［M］.北京：军事科学出版社，1993.

［4］徐南荣，仲伟俊.科学决策理论与方法［M］.南京：东南大学出版社，1995.

［5］张战平，杨争新.车载式122榴弹炮单炮作战能力分析［J］.射击学报，2005（2），9-11.

［6］王曙光，王瑞林.单兵综合作战系统效能指数的确定方法［J］.火力与指挥控制，2007，32（3），53-55.

［7］张俊学，王书敏，董树军.军事运筹理论与方法［M］.北京：解放军出版社，2002.

M odelof Operational Effectiveness Evaluation in Amphibious Armoured Vehicle

LIU Fen-liang，LUOQuan，LIZe-en
（NavalMarine Academy，Guangzhou 510430，China）

In the light of the actual requirement of landing operations，an improved ADCmodel is brought out by introducing index of battlefield environment and viability in battlefield，which was analyzed and figured out by the method of exponential and AHP.It optimizes the evaluation index system of the battle operation effectiveness of amphibious armoured vehicle，making the result of the evaluated effectivenessmore scientific and closer to the practice.

amphibiousarmoured vehicle，improved ADC，method ofexponential，AHP

E923.16；O224

A

1002-0640（2014）02-0169-04

2013-02-21

2013-03-27

刘芬良（1974- ），男，湖南双峰人，硕士。研究方向：两栖作战战术理论与应用。