基于现场试桩的多模型长桩稳定性分析

刘成毅，王蔚佳，王永华

（1.四川建筑职业技术学院，四川 德阳618000；2.重庆大学 土木工程学院，重庆400045；3.广西建工集团第一安装有限公司，南宁530001）

对非嵌岩段桩周土体软弱、桩上部自由长度较大的长桩，有可能先于桩底持力层和桩本体材料的强度破坏而发生屈曲失效，设计时应进行桩的轴压稳定性计算，其轴压稳定系数φ需由桩的计算长度lc确定。确定桩的计算长度需要分析桩土相互作用时的桩体纵向屈曲特性，该领域的应用研究始于20世纪60年代，中国学者的研究与国外基本同步［1－4］。至20世纪90年代，随着端承长桩在建筑、桥梁等工程中的大量使用，桩身屈曲稳定问题受到进一步重视。依据文克尔（Winkler）假设的线弹性地基反力模型因在数学处理上比较简单，当桩的挠曲变形较小时，假设与实际比较吻合，因此在桩的压屈稳定研究中被普遍采用。学者们曾提出了数种线弹性地基反力分布的模型，如“常数法”、“K 法”、“C法”和“m法”等，分别适应于某类特征的土体结构。例如，“常数法”适用于比较坚硬的土体和岩石，可用于分析部分打入冻土内桩的屈曲问题［5］；而“m法”和“C法”比较适合粘性土和砂性土［6－7］。但以上各种地基模型都被认为存在一定局限性。如“m法”地基模型，由于地基反力系数不会随着深度增大而始终保持近线性增长关系，用于长桩时会与实际情况存在偏差；而“C法”模型的地基深度x的指数ω，根据不同土体特征，取值可能在0～2范围［8］，对ω值恒取0.5并不合理，等等。因此有学者提出在桩的稳定设计计算中可采用折线法［9］，即地面以下一定深度按“m法”，更大深度时地基系数k可取常数，或按“C法”计算［10］（ω＝0.5）。然而，目前除“m法”地基模型外，要通过现场试桩确定其他模型的相关参数还存在一定难度，用于桩屈曲稳定分析时所采用的地基模型还主要是基于试桩获取单参数地基比例系数的“m 法”［6，11－13］。虽然文献［14］应用 Rayleigh－Ritz法对“常数法”、“C法”、“m 法”和“Prakash法”等地基反力模型中的桥梁基桩屈曲性质进行了分析，但各模型参数不是由同一基桩的现场试验获得，还不能比较采用不同地基模型时桩的屈曲稳定性计算所产生的差异。为此，笔者仍依据文克尔假设，将桩土相互作用体系简化成离散集中弹性支撑结构，应用传递矩阵建立适应几种不同地基反力分布规律假设的数学模型，力求通过现场试桩获取相关模型参数并对桩的屈曲稳定性进行分析。

1 桩土相互作用体系的弹性离散简化

对桩侧地基弹性反力模型离散简化可采用纽玛克（Newmark）法［8，15］。基本概念是把埋入土中的桩体划分成若干段，通过对每段桩侧土体反力的弹性系数进行积分，将其等效转换成一个对桩体产生横向支撑作用的弹簧的刚度系数，使复杂的桩土相互作用体系转化成较为简单的弹簧支撑连续压弯结构模型。然而，桩侧地基反力是桩土相互作用的结果，桩的挠曲侧移也是决定地基反力大小的重要因素。考虑分割桩段两端存在不等值挠曲侧移，应用力矩平衡等效原理简化确定集中弹簧力。常用的弹性地基反力数学模型可用式（1）表示：

式中：q（）x为地基反力；x是桩在地面或局部冲刷线以下的计算深度；m是地基系数的比例系数；b0是桩身计算宽度；ω是反映地基反力随深度变化的指数；y为桩身挠曲位移；k即为地基系数。对地基为任意分层构造的非嵌岩桩体，将其分割成若干小段，如图1（a）。各段桩侧土体在分段节点深度处的地基系数ki按式（2）计算，并符合对该层地基模型的分布规律假设。本文将m和ω同时作为变量以确定地基系数k的方法称为曲线法。

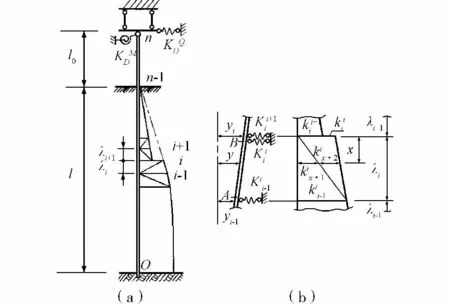
图1 桩侧地基反力等效弹簧支座简化模型

将各段桩侧土体线性简化成两组刚度系数呈三角形分布的小弹簧群。对图1（a）中取出的λi桩段（见图1（b）），设 K和K分别为两端集中弹簧的刚度系数。考虑桩段两端不等值侧移因素，集中弹簧力Kyi－1按式（3）计算。

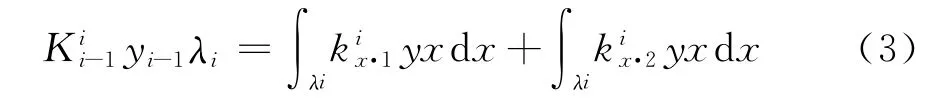
可得

同理可得

2 建立桩土体系的传递矩阵

对图1（b）中λi桩段，设EI为桩的抗弯刚度，N是该段桩的轴力。应用结构力学原理建立i－1、i点集中弹簧K和K内侧AB桩段的变形及内力方程。由于式（4）、（5）中λi桩段两端弹簧力均与该桩段两端位移相关，因此需对AB桩段的变形及内力方程进行修正。桩段在i－1和i节点处，集中弹簧上下两侧的侧移、转角和弯矩相同。在i－1节点处，

在i节点处，

通过式（6）、式（7）将地基反力与桩段两端位移的相关性引入桩段变形及内力方程，修正后的λi桩段变形及内力方程可表示为式（8）～（11）。对伸出地面的桩段无需修正，

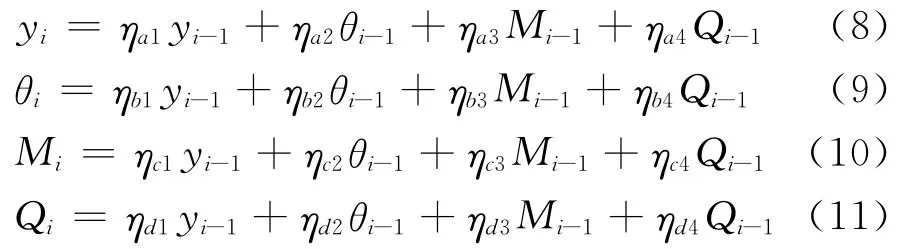
式（8）～（11）中：ηa1～ηd4共16个系数是与桩的轴向压力N、抗弯刚度EI、桩分段长度λ以及桩侧地基比例系数m和地基反力深度变化指数ω有关的系数。由式（8）～式（11）构建桩身λi段的场矩阵U和杆端状态矩阵S。由i－1节点向i节点的传递关系如式（12）所示。

由桩底部向顶部n端的传递矩阵方程为

3 基桩多模型参数测定和屈曲分析

基桩屈曲属于小挠度侧移问题，对于钢筋混凝土桩，当水平加载力不超过临界载荷时，可认为桩体开裂微小，桩体抗弯刚度具有较好的整体连续性。应用传递矩阵，结合基桩水平载荷试验可以确定不同地基假设模型的相关参数。

3.1 基桩多模型参数测定

对于桩底部嵌岩端承桩，桩底部y0、θ0为零，展开桩顶部n端状态向量可得变形与内力计算式如式（14）～（17）。对桩底部非嵌岩状态，改设M0和Q0为零而保留y0和θ0项即可。先设桩顶处于试桩状态，n点是桩顶地面试验受力点，在试桩仅有水平加载力时，式（16）中Mn为零。

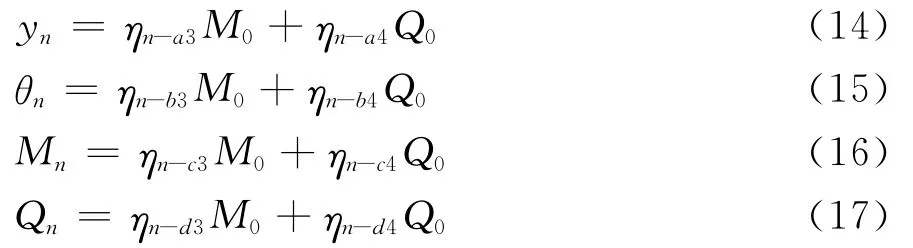
将Qn改用水平加载力Hs表示，消去式（14）至（17）各式中M0和Q0，将不同地基假设模型的相关参数代入传递矩阵运算式，由式（18）、（19）可得到桩的力作用点截面水平侧移ynj和转角θnj的搜索计算值。

对于m法和曲线法模型，可直接将式（2）中m和ω设为待搜索变量。对于折线法模型，桩体依照图1分段建立传递矩阵时，可将m值和地基系数k的转折点深度lZ设为待搜索变量。试验中实测桩顶水平位移ync和转角θnc，与搜索计算值ynj和θnj的差值分别为Δy＝ync－ynj和Δθ＝θnc－θnj。以Δy和Δθ分别等于零为目标，可以利用计算机编程搜索桩的不同假设地基模型的相关参数。设定ω＝1，用式（18）和（19）其中之一，可用寻根法直接搜索地基系数的比例系数m值；求解曲线法之m和ω时，先在桩侧土体m的可取值范围内初选m值，应用式（18）和（19）分别获得初值ωy和ωθ，并得到Δω ＝ωy－ωθ。对m增或减步长，得到Δω的新值，从而判断Δω的收敛方向。当Δω正负变号时再精细迭代获得m和ω的数字解。折线法求解m值和转折点深度lZ可用相同算法。

计算地基模型相关参数时一般可不计桩的轴向压力，运算时对轴力N赋与一个很小的数即可；对大直径钢筋混凝土端承桩，计算桩段轴力可取该段以上桩体自重。

3.2 基桩屈曲特征方程

经试桩获取不同地基反力分布的模型参数之后，应用传递矩阵可对基桩按不同地基模型进行屈曲稳定计算与分析。承台对桩顶约束可表示为图1（a）形式，此时桩顶n点的力与力矩平衡方程为式（20）和式（21），由此可得桩的屈曲特征方程。表1给出4种典型桩顶约束条件的基桩屈曲特征方程。利用计算机可对桩的轴压临界力Ncr搜索求解。桩的计算长度由式（22）计算。

表1 桩顶不同约束形式的屈曲特征方程

4 算例分析

根据建筑基桩检测技术规范［16］的技术方案，单桩水平静载试验采用分级加载方式，试桩的地基模型参数是按分级测定的多组当量值。在实际工程应用中究竟应取哪一组数据作为屈曲稳定设计的依据，还需要更多的试验与论证。但通过已收集的7例钢筋混凝土基桩水平载荷试验资料，对各例基桩在加载不超过试验临界载荷时，用不同地基模型进行比较分析，发现不同地基反力模型对桩的稳定性影响具有某些相同的特征。7例基桩包括灌注桩和打入桩，桩侧土为较普遍的杂填土、黏土、粉土、砂土、砾石分层或夹杂等结构。根据试桩测得地面处桩的侧移ync和转角θnc建立不同地基反力模型，然后虚拟桩在地面以上伸出长度。现用灌注桩和打入桩各一例，采用临界载荷数据组分析如下。

算例1：某工业构筑物钻孔灌注桩，桩的入土深度32.5m，桩径0.6m，桩身抗弯刚度EI＝166.38MN·m2。水平试验加载至105kN临界载荷时，测得桩的水平位移为4.53mm，转角为0.002 06rad。对于m法模型，按基桩检测规范［16］推荐公式和应用本文方法计算的m值分别为17 363和17 208kN／m4，二者非常接近。按曲线法计算得m和ω值分别为16 745kN／m4和0.716；折线模型的m值和转折点深度lz分别为20 176kN／m4和1.123m。

为比较不同地基反力模型对桩的稳定性影响程度，图2和图3基于不同地基反力模型，对表1中不同桩顶约束形式绘制了桩计算长度与伸出地面长度的关系曲线。《建筑桩基技术规范》（JGJ 94）的方法是将桩满足α＝4.0的换算深度处视为固定端，忽略上部土体对桩的水平支撑作用，对表1中桩顶铰接和固定形式分别取计算长度系数为0.7和0.5。

图2 灌注桩桩顶自由和铰接时的l0－lC曲线

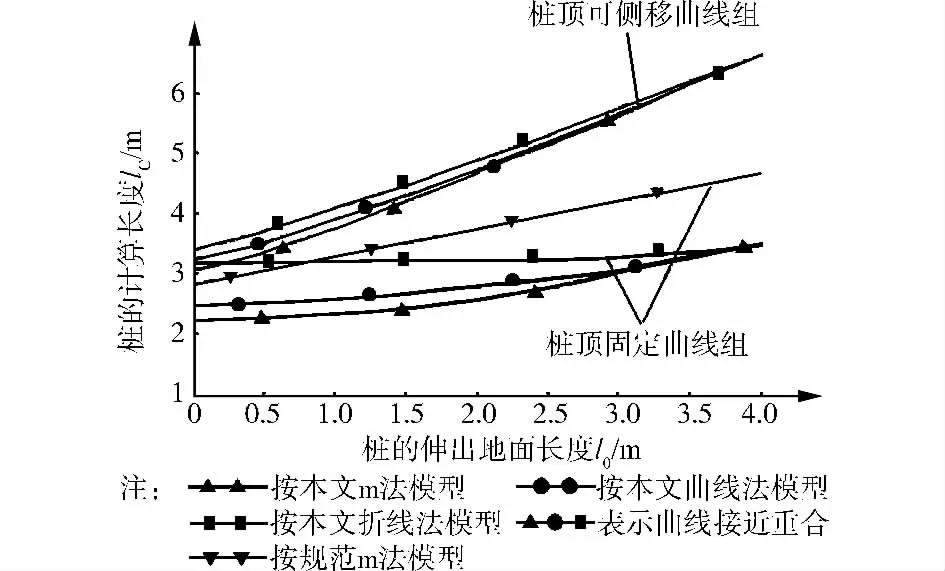
图3 灌注桩桩顶固定和侧移时的l0－lC曲线

算例2：预制打入桩［17］，桩的入土深度20m，桩截面400mm×400mm，水平试验临界载荷30kN，测得桩水平位移为2.08mm，转角0.001 12rad。按基桩检测规范公式和本文方法计算的m值分别为21 448kN／m4和21 372kN／m4。按曲线法计算得m和ω值分别为20 401kN／m4和0.831；折线模型的m值和转折点深度lz分别为23 726kN／m4和1.157m。图4和5是不同地基反力模型的桩计算长度与伸出地面长度的关系曲线。

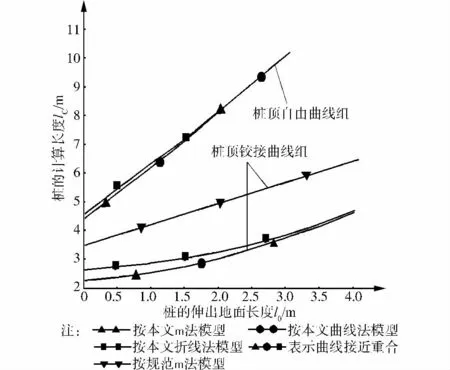
图4 打入桩桩顶自由和铰接时的l0－lC曲线

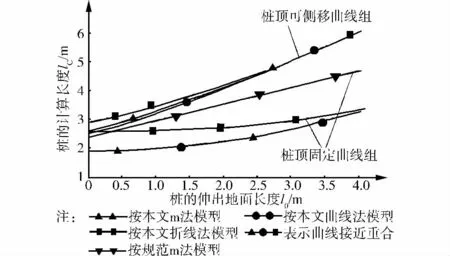
图5 打入桩桩顶固定和侧移时的l0－lC曲线

比较图2、图3及图4、图5可知，两例基桩不同地基反力模型的桩计算长度与伸出地面长度的关系曲线分布极为相似。桩顶自由状态的l0－lC曲线是桩的计算长度取值上界，以下是桩顶约束刚度系数K和K取不同值时曲线存在的空间。对桩顶被有限约束的基桩，桩顶约束刚度系数K和K的取值是一个复杂问题，还有待工程与学术界进一步研究。

5 结论

通过基桩现场水平载荷试验测定桩顶水平位移和截面转角双参数，可以建立不同地基反力模型；因此可以对同一实际地基土体构造，用不同地基反力模型对长桩稳定性进行对比分析。算例计算结果表明：

1）用m法、曲线法、折线法3种地基反力模型分析桩的稳定性，当基桩无伸出段或伸出地面以上长度不大时，用折线模型所得的桩屈曲计算长度会大于前两种模型，且在桩顶固定约束时最为显著。随着桩的伸出段长度增加，3条l0－lC曲线基本重合，选用不同地基反力模型主要对无伸出段或伸出地面长度较短的桩的稳定性产生影响。对桩顶无侧移铰接和固定构造，m法、曲线、折线3种模型的l0－lC曲线较为平缓。说明桩顶侧向约束对桩的稳定性起到重要作用。

2）对于桩顶固定的构造，依照《建筑桩基技术规范》（JGJ 94）简化方法计算无地面伸出段和伸出长度较小的长桩的计算长度，与笔者用3种地基反力模型的计算结果比较，并无明显安全裕度优势，甚至可能小于折线法模型的计算长度，出现偏于不安全的情况，对此工程中应给与重视。桩顶自由曲线组远高于用简化方法计算的桩顶无侧移铰接的l0－lc曲线，对于桩顶转动和侧向约束较弱的构造，不能盲目简化为桩顶无侧移铰接形式。

［1］Toakley A R.Buckling loads for elastically supported struts ［J］.Journal of Engineers Mechanics and Foundations Division，ASCE，1965，91（3）：205－231.

［2］Reddy A S，Valsangkar A J.Buckling of fully and partially embedded piles ［J］.Journal of Soil Mechanics and Foundation Division，ASCE，1970，96（6）：1951－1965.

［3］胡人礼.关于桥粱基础采用m法计算土壤抗力的几个问题［J］.铁路标准设计通讯，1973（1）：18－26.Hu R L.A few problems in the calculation of side resistance by m method for bridge piles ［J］.News Report in Railway Standard Design，1973（1）：18－26.

［4］朱大同.端部嵌固桩的计算长度［J］.铁路标准设计通讯，1974（5）：27－29.Zhu D T.Calculation length of piles fixed in both sides［J］.News Report in Rail way Standard Design，1974（5）：27－29.

［5］Budkowska B B，Szymczak C.Initial post－buckling behavior of piles partially embedded in soil ［J］.Computers and Structures，1997，62（5）：831－835.

［6］杨维好，任彦龙.端部嵌固桩的稳定性分析［J］.岩石力学与工程学报，2000，19（3）：380－382.Yang W H，Ren Y L.Axial buckling analysis for bottomfixed pile ［J］.Chinese Journal of Rock Mechanics and Engineering，2000，19（3）：380－382.

［7］赵明华，徐卓君，马缤辉，等.倾斜荷载下基桩C法的幂级数解［J］.湖南大学学报：自然科学版，2012，39（3）：1－5.Zhao M H，Xu Z J，Ma B H，et al.Power series solution for pile based on C－method under inclined loads［J］.Journal of Hunan University：Natural Sciences，2012，39（3）：1－5.

［8］赵明华.桥梁桩基计算与检测［M］.北京：人民交通出版社，2000：49－71.

［9］王成，董倩.超长桩稳定承载力计算新方法［J］.岩土力学，2005，26（Sup）：180－182.Wang C，Dong Q.A new method of calculating stable bearing capacity for overlength piles［J］.Rock and Soil Mechanics，2005，26（Sup）：180－182.

［10］姚文娟，傅祥卿，仇元忠.超长桩的屈曲荷载计算［J］.地下空间与工程学报，2009，5（3）：463－467.Yao W J，Fu X Q，Qiu Y Z.Buckling loads for superlong piles［J］.Chinese Journal of Underground Space and Engineering，2009，5（3）：463－467.

［11］Gabr M A，Wang J J，Zhao M.Buckling of piles with general power distribution of lateral subgrade reaction［J］.Journal of Geotechnical and Geoenvironmental Engineering，ASCE，1997，123（2）：123－130.

［12］何雄君，周莉娜，王启武.用有限元法求解基桩的屈曲临界载荷［J］.武汉理工大学学报，2003，25（6）：25－27.He X J，Zhou L N，Wang Q W.Solution of buckling loads for piles with FEM ［J］.Journal of Wuhan University of Technology，2003，25（6）：25－27.

［13］赵明华，邹新军，刘光栋.基于m法的高承台嵌岩灌注桩初始后屈曲性状分析［J］.岩石力学与工程学，2005，24（22）：4116－4119.Zhao M H，Zou X J，Liu G D.Behavior analysis of initial post－buckling of socketed filling pile with highrise pile cap by m method ［J］.Chinese Journal of Rock Mechanics and Engineering，2005，24（22）：4116－4119.

［14］杨健，沈惠申，张乐.桥梁基桩的屈曲荷载计算［J］.上海交通大学学报，2000，34（4）：533－541.Yang J，Shen H S，Zhang L.Buckling loads for bridge piles ［J］.Journal of Shanghai Jiaotong University，2000，34（4）：533－541.

［15］苏静波，邵国建，刘宁.基于曲线法的水平受荷桩非线性有限元分析［J］.岩土力学，2006，27（10）：1782－1785.Su J B，Shao G J，Liu N.Nonlinear finite element analysis of piles under lateral load based on P－y curves［J］.Rock and Soil Mechanics，2006，27（10）：1782－1785.

［16］中华人民共和国建设部.GJ 106—2003建筑基桩检测技术规范［S］.北京：中国建筑工业出版社，2003.

［17］史佩栋.实用桩基工程手册［M］.北京：中国建筑工业出版社，1999：864－866.