一种标定相机内方位元素的迭代算法

王东杰 张继友 马丽娜

（北京空间机电研究所，北京 100094）

0 引言

相机标定技术是从拍摄的图像信息和标定参照物中提取相机的内外方位元素，从而建立空间三维坐标系中位置、方向信息与图像二维坐标系间的精确映射关系。相机的内方位元素指相机的主点、主距、畸变等参数，外方位元素指相机位置和方向等参数[1]。相机内外方位元素的标定在摄影测量、图像校正、三维重建以及机器视觉等诸多领域具有重要作用。相机自标定方法为近几年兴起的一种相机标定技术，该方法由一台或多台相机从不同的位置和方向对一个尺寸已知的棋盘格模板拍摄多幅图像，以模板和图像的对应关系求解出内外方位元素，具有标定操作过程简单易行、实验结果精度较高的优点。

本文介绍一种利用消失点理论得到迭代算法初值以求解相机内外方位元素的B双空间几何自标定方法。不同于张氏标定法[2]和Tsai的两步标定法仅利用标定图像的点信息，B双空间几何法基于消失点理论，利用二维棋盘格标定图像中点、线、面间固有的几何关系获得相机参数的初始估计值[3]，采用牛顿—拉夫逊（New ton-Raphson）算法对非线性的共线方程进行迭代求解。New ton-Raphson迭代算法能够在保证计算效率的同时获得较高的结果精度[4-5]，图像中的棋盘点坐标由Harris角点提取算法得到，作为已知条件，通过使用张氏标定法中的实验数据进行对比性实验，实验结果表明，两种方法得到的结果标定精度十分接近，证实本文算法能够用于相机内外方位元素的标定，标定精度较理想。

1 迭代算法

本文利用New ton-Raphson算法对由相机参数的初始估计值得到的非线性共线方程进行迭代求解，以得到精确的相机参数标定结果。相机参数的初始估计值由B双空间几何理论得到，而本文所采用的畸变模型包含3个径向和2个切向畸变系数，比张氏标定法只包括2个径向畸变系数的畸变模型能够更精准地给出畸变值。整个迭代算法的流程如图1所示。

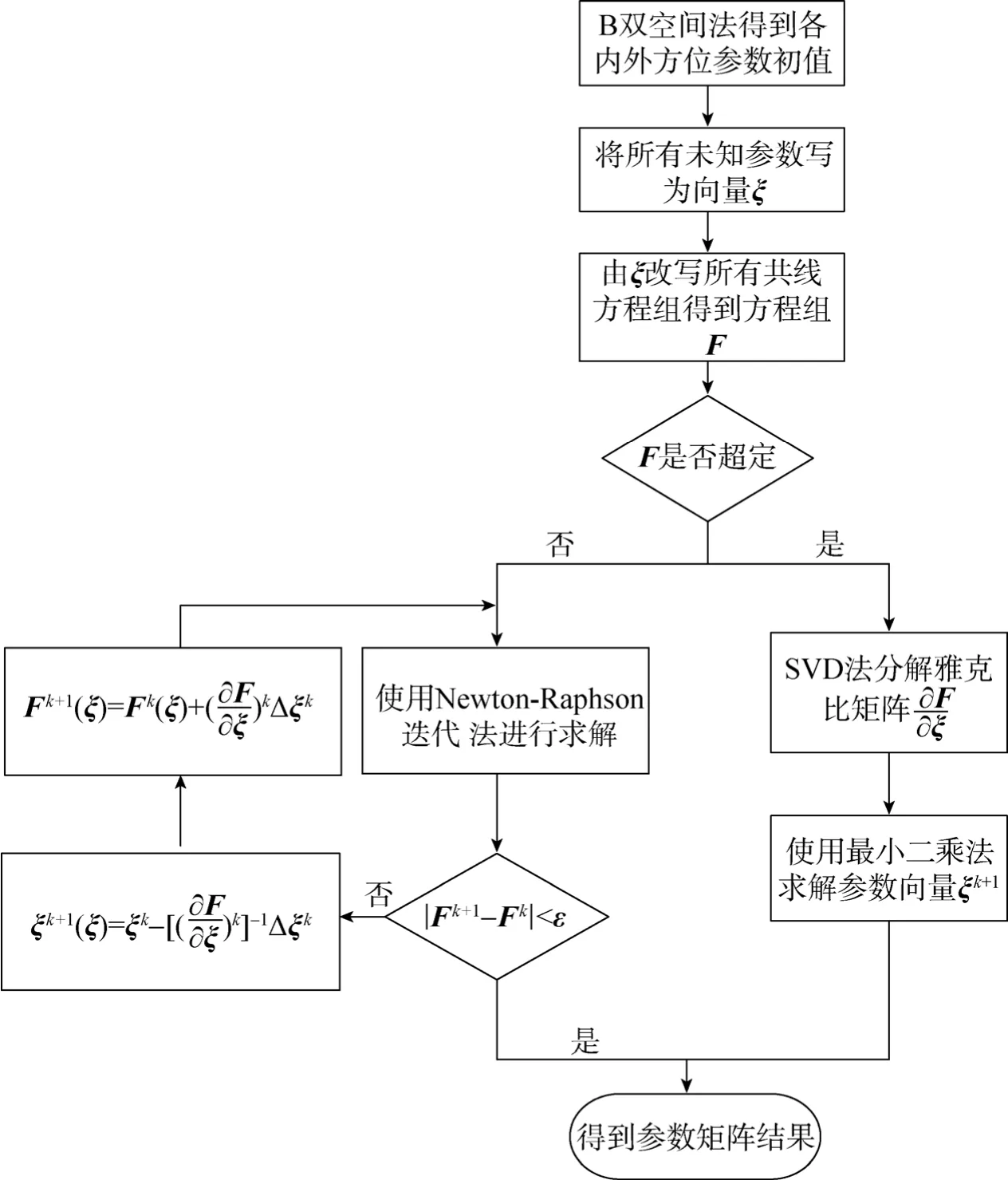
图1 迭代算法流程Fig.1 The flow chartof the iterativemethod

1.1 共线方程

设模板坐标系和图像坐标系中点的坐标分别为（X,Y,Z）和（x,y,z）。图像坐标系的原点在模板坐标系中的坐标为（XC,YC,ZC）。图像坐标系相对于模板坐标系的方向由一个3×3的旋转矩阵R表示。R的9个元素rij（i=1,2,3；j=1,2,3）非独立，通过欧拉角变换，R可以视为分别绕3个坐标轴旋转的3个旋转矩阵的乘积[6]。设绕x,y,z轴旋转的角度分别为ω，φ，κ，则

式中

以上3个方程相乘后得：

由式（2）可知，R的各行（列）向量相互正交。

在标定过程中，模板中取棋盘角点的左上点为原点，坐标值为实际距离值。对于理想相机模型，模板上一点（X,Y,Z）投影到图像坐标系后其坐标为（x,y）。但由于图像畸变，其实际坐标为（x′,y′）。

模板坐标系和图像坐标系之间的关系为

式中 Δx,Δy为包括对称和非对称畸变的畸变模型；xp,yp为图像坐标系中的主点；fx,fy为主距，fx=fdx，fy=fdy，f为相机焦距，dx,dy分别为像面上X,Y方向上的像元尺寸。Δx,Δy的计算式为

设棋盘模板上的棋盘角点数量为m，相机从不同位置拍摄的模板图像数量为n。对于每个相机的放置位置，其对应的图像上能检测到并能计算出坐标的棋盘角点的数量为mi（i=1,2,3,…,n）个，有mi≤m，因此所有未知数数量为6n+9，所有共线方程的数量为，且不超过所拍摄所有图像中的棋盘角点数量总数2mn，在检验过程中的超定方程为

1.2 求解算法

1.2.1 迭代计算

与内外方位元素有关的超定方程可使用最小二乘法求解。首先将方程改写成一个简易的形式，定义一个包括所有未知量的向量为

式中l=mi-1+j，m0=0，j=1,2,3,…,mi，i=1,2,3,…,n；χj=(Xj,Yj,Zj)为模板坐标系中第j个棋盘点的坐标向量；χC,i=(XC,i,YC,i,ZC,i)为相机第i个位置所拍摄图像的坐标原点在模板坐标系中的坐标向量。单位向量rk,i为第i组欧拉角(ωi,φi,κi)对应的旋转矩阵R中的第k列列向量[6]。

对式（9）用迭代算法进行求解，假设解向量ξ在第k次迭代得到，则式（9）左边可以用第k+1次迭代时的有限泰勒级数表示：

式中 Δξk为一个包含6n+10个元素的列向量；δ为一个包含个元素的列向量；行、6n+10列的雅克比矩阵。根据New ton-Raphson迭代算法，令δk+1=0，得到：

式中wj为由矩阵A的奇异值组成对角矩阵中的第j个元素。V■■di ag(1/wj)■■UT为矩阵A的伪逆矩阵。在本文中，雅克比矩阵的伪逆阵通过奇异值分解法得到，在ξk+1处的解向量通过最小二乘法得到。使用奇异值分解法的优点是当雅克比矩阵为奇异矩阵或病态矩阵时，上述过程依然有效。计算雅克比矩阵的条件数，即最大与最小奇异值的比值，若条件数的倒数小于10–p（p为条件数评价标准的指数），则将所有小于最大奇异值10–p倍的奇异值设为0，可以排除舍入误差对解造成的干扰，本文中的计算为双精度计算，令p=12。

1.2.3 收敛标准

文献[6]中指出New ton-Raphson方法在初始估计的迭代值非常接近方程的解时，即迭代结果已满足精度要求时收敛。本文结束迭代计算过程的收敛标准为

式中ε为一个视计算情况而定的一个无限小的数。

另一种收敛标准是检验解向量 Δξk的L∞范数的变化[6]。对于上述两种标准，都在ε= 10-8、迭代 10～20次时达到收敛。收敛结果不包含二次偏导项，与标准的New ton-Raphson算法不同，这是因为在采用最小二乘法解方程组时，有些情况下雅克比矩阵可能有较大的条件数。

1.2.4 万向节死锁

φ= π/2时，旋转矩阵为

式（14）说明，解向量仅依靠ω和κ的变化，独立未知量的数量减少了一个，这种现象称为“万向节死锁”。对于这种情况，检验结果显示收敛的解向量中ω和κ为随机值，但二者的差值正确。对于φ= π/2的万向节死锁情况无需特殊措施。由式（14）可以看出，相比于ω、κ各自的值，ω-κ的差值更重要，因为最终要得到模板点坐标和图像点坐标之间的映射关系[6-7]。

1.3 求解算法

在透视投影下，三维空间中的平行线映射到图像平面上相交于一点，称为消失点，不同消失点的连线称为消失线。不同于成像平面上的其他特征点，消失点和消失线蕴含了直线的方向信息，比边缘、拐角等特征更具鲁棒性。对消失点和消失线的分析可以提供大量的场景三维结构和方向信息[7]。本文利用B双空间几何方法对相机内外方位元素进行求解，作为迭代算法的初始估计值。B双空间几何法通过B双空间的转换将消失点和消失线映射成容易计算的有限向量[8-9]，利用平行和正交的向量关系可以计算出消失点的值，进而得到相机内外方位元素，作为迭代算法的初值[3,9-11]。

1.3.1 焦距值的确定

B双空间几何中点线面关系如图2所示，假设正方形ABCD经透视投影后，正方形的4个点在以相?机主点为原点的坐标系中的坐标分别为，其坐标值（x1,y1,1），（x2,y2,1），（x3,y3,1），（x4,y4,1）由角点提取算法给出，坐标值中的“1”为在齐次坐标系中的有限远平面，点V1为向量的消失点，点V2为向量的消失点，为与面ΠH相关的消失线。

图2 双空间几何中点线面关系Fig.2 The relationship among points,lines and planes in B-dual-space geometry

则由双空间几何关系的特性可得到：

由于ABCD为正方形，其对角线相互垂直，利用这条约束可得到两对角线与消失线间的关系为

由于V1⊥V2、V3⊥V4，可得：

式中V≅［abc］T为各消失点的像元坐标，a、b、c为像元坐标值，i=1,2,3,4。由式（17）

iiiiiii可得：

至此可得到2个主距的初始估计。

1.3.2 其他参数的确定

由文献[8,11-12]可知，在利用棋盘模板进行标定的过程中，不能确定主点位置（xp,yp）。因此在初始估计阶段，将主点位置假设为像面的中心，即为像面X、Y方向上的像元个数。通过迭代算法求解出主点的实际值。

根据文献[8]中双空间几何理论中总结的消失线特性可知，消失线向量正比于平面ΠH的法向量，因此可由其得到棋盘模板平面相对于图像平面的方向，即可通过向量得到外方位元素中表示相机方向的角度值(ω，φ，κ)。此外，文献[8]中指出模板坐标系的原点与主点之间的距离也可通过消失线向量λH求出，于是可得到外方位元素中表示相机位置向量（XC，YC，ZC），相机的外方位元素的初始估计值为(XC,YC,ZC,ω,φ,κ)。

1.4 重投影误差

作为标定结果精度的衡量标准，重投影误差定义为图像点检测值（xi，yi）和根据内外方位元素(k1,k2,k3,p1,p1,xp,yp,fx,fy)、模板点坐标（Xi,Yi）带入畸变模型后进行计算得到的图像坐标点（xi′,yi′）之间的偏差。重投影误差的计算通过建立数据拟合目标函数得到：

从上式看出，目标函数是由一组残量平方和组成，若得到的目标函数值越小，则数据拟合得越好，求得的参数值越准确。本文算法不是直接求解非线性的畸变模型，而是将其转化成求解非线性最小二乘问题，通过非线性优化算法多次迭代，最后得到使目标函数值最小的参数值，降低了求解难度。

2 与张氏标定法的比较

张正友提出了基于二维平面模板的标定方法（张氏标定法）[13-14]，张氏标定法只要从不同角度对同一标定平面(标定板)拍摄2幅以上的图像，就可以求出相机的内外方位元素。由于该方法不需要知道标定板移动的具体位置信息，而且标定板的制作简单，因此这种方法简单、灵活。其整个自标定过程可分解为以下几个步骤：

1）分别以图像幅数范围、网格板角度范围等参数拍摄照片；

2）对所拍摄照片进行图像处理，用Harris角点提取算法提取角点；

3）利用棋盘格标定板在世界坐标系的坐标和相应的图像角点坐标计算每幅图像的单应性矩阵；

4）由所得单应性矩阵，根据自标定算法求解出内方位元素矩阵初值；

5）设计畸变模型；

6）将由内方位矩阵和畸变模型计算所得的角点坐标和实际图像角点坐标代入数据拟合函数进行拟合，并通过非线性优化算法进行迭代，得到内方位矩阵和畸变系数的精确值。

本文提出的基于B双空间几何的相机自标定方法与张氏标定法类似，所需靶标同样为尺寸精准的棋盘格标定板，标定过程也同样需要上述6个步骤。但不同之处在于：

1）确定内方位元素矩阵初值的算法；

2）畸变模型；

3）非线性优化迭代算法。

两种算法的异同点见表1。

表1 两种算法的比较Tab.1 Comparison between Zhang’s and our calibration algorithms

由表1可知，本文提出的算法通过基于消失点理论的B双空间几何法，充分利用二维棋盘格标定图像中点、线、面间固有的几何关系获得相机参数的初始估计值；通过New ton-Raphson迭代算法在保证非线性优化迭代计算效率的同时获得较高的结果精度；畸变模型能更加详细地给出畸变值。

3 实验

对于本文提出的标定方法，利用文献[2]提供的测试数据进行了实验，如图3所示，并将测试结果进行对比，见表2。张氏标定法基于Levenberg-Marquardt算法对得到的内方位元素初值进行优化迭代求解，并用相同的数据目标拟合函数进行重投影误差计算，作为评价标定结果精度的标准。

图3 张氏标定法使用的标定图像Fig.3 Calibration Images of Zhangmethod

表2 张氏标定法与本文算法的结果及误差比较Tab.2 Comparison between Zhang’sand our calibration algorithm s 像元

由表2可以看出，虽然两种算法用于优化的初值相差较多，但经过优化后得到的终值十分相近。但张氏标定法得到的重投影误差为0.335个像元[14]，本文算法得到的重投影误差为0.265个像元，这表示本文方法计算出的相机内方位元素精度更高，更加接近实际相机成像模型。由于畸变模型不同，镜头畸变系数不具有可比性，但是本文的畸变模型有5项参数，能够更加准确反应实际镜头的畸变情况。

4 结束语

本文介绍了一种利用相机在不同位置拍摄的多幅图像中的特征点信息，计算相机内外方位元素的迭代计算方法。该方法用B双空间几何的特性，利用消失点、消失线理论得到迭代方法的初值。在无需进行干预初始估计值的情况下，通过迭代计算得到精度较高的内方位元素值。通过与张氏标定法的对比实验来比较两标定法的精度，实验结果表明，本文介绍的算法误差更小，其标定的相机参数也更加精确，能够用于相机内方位元素的标定，且标定精度较理想。

References)

[1] 谭启蒙,胡成威,高升.空间机械臂视觉相机内参标定技术研究[J].航天返回与遥感,2013,34(6):74-81.TAN Qimeng,HU Chengwei,GAO Sheng.Research on Calibration of Intrinsic Parameters for Space Manipulator Camera Based on 2D Planar Pattern[J].Spacecraft Recovery&Remote Sensing,2013,34(6):74-81.(in Chinese)

[2] ZHANG Zhengyou.A Flexible New Technique for Camera Calibration[EB/OL].[2014-03-20].http://research.microsoft.com/users/zhang/Calib/Calibration/Calib.txt.

[3] 吴刚,唐振民.B双空间几何中基于消隐点的摄像机标定[J].计算机工程与应用,2009,45(24):4-8.WU Gang,TANG Zhenmin.Camera Calibration Based on Vanishing Points in B-dual-space Geometry[J].Computer Engineering and Applications,2009,45(24):4-8.(in Chinese)

[4] 熊磊,刘国栋,刘小勇,等.数字图像相关中基于非线性灰度改变模型的灰度梯度迭代算法[J].机床与液压,2012,40(13):70-72.XIONG Lei,LIU Guodong,LIU Xiaoyong,et al.Gray-gradient Iterative Algorithm Based on Nonlinear Intensity Change Model in Digital Image Correlation[J].Machine Tool&Hydraulics,2012,40(13):70-72.(in Chinese)

[5] Marzan G,Karara H.A Computer Program for Direct Linear Transformation Solution of the Collinearity Condition and Some Applications of it[C].Proc.APSSymp.on Close-Range Photogrammetric Systems,Urbana,1975:420-476.

[6] Ravi S.A Method to Solve Interior and Exterior Camera Calibration Parameters for Image Resection[J/OL].[2014-03-20].http://www.nas.nasa.gov/Research/Reports/Techreports/1999/nas-99-003-abstract.htm l.

[7] 吴闻.游戏程序设计中若干问题的探讨[J].电脑知识与技术,2009,5(16):4331-4336.WU Wen.Discussion of Some Problems in Game Programm ing[J].Computer Know ledge and Technology.2009,5(16):4331-4336.(in Chinese)

[8] 梅雪,夏良正,李久贤,等.一种三维场景的消失点检测算法[J].信号处理,2007,23(6):924-926.MEIXu,XIA Liangzheng,LI Jiuxian,et al.A Vanishing Point Detection Algorithm for 3D Scene[J].Signal Processing,2007,23(6):924-926.(in Chinese)

[9] Bouguetj JY.VisualMethods for Three-dementional Modeling[D].California:California Institute of Technology,1999.

[10] Jean Y B,Pietro P.Camera Calibration from Points and Lines in Dual-Space Geometry[EB/OL].http://www.vision.caltech.edu/bouguetj/calib.doc.

[11] Jean Y B,Pietro P.Closed-form Camera Calibration in Dual-space Geometry[EB/OL].http://www.vision.caltech.edu/bouguetj/calib.doc.

[12] Tsai R Y.A Versatile Camera Calibration Technique for High Accuracy 3D Machine Vision Metrology Using off-the-shelf TV Cameras and Lenses[J].IEEE J.Rovotics Automat,1987,3(4):323-344.

[13] WANG L L,TsaiW H.Camera Calibration by Vanishing Lines for 3D Computer Vision[J].PAM I,1991,13(4):370-376.

[14] ZHANG Zhengyou.Flexible Camera Calibration by View ing a Plane From Unknown Orientations[J].IEEE International Conference on Computer Vision,1999(1):666-673.

[15] Abdel-Aziz Y,Karara H.Direct Linear Transformation from Comparator Coordinates into Object Space Coordinates[C]//Proc.APSSymp.on Close-Range Photogrammetric Systems,Urbana,IL.1971:1-48.

[16] Bell JH,M cLachlan BG.Image Registration for Pressure-Sensitive PaintApplications[J].Experiments in Fluids,1996(22):78-86.