关于太阳耀斑观测的地图匹配算法实现

李恺 张晗 康晓军

（北京机电研究所，北京 100094）

0 引言

当卫星在轨飞行过程中要求进行太阳闪耀观测时，控制软件在判断卫星星下点所在位置满足观测条件后，才可进行观测。因为卫星星下点与海岸线地图的相对位置实时变化，所以在整个观测过程中，需要根据最新更新的轨道要素数据，实时判断观测条件是否满足，这要求判断算法快速完成任务。

实际工程中，将以星下点为中心的矩形区域与海岸线地图的位置关系作为判断能否进行太阳闪耀观测的条件。当矩形处于海洋区域时，可以观测；当矩形与海洋区域相交或在陆地区域时，不可以观测。

上述问题类似于计算机图形学[1]中，利用指定区域对指定不规则多边形进行截取，并显示截取部分。但本文只需确定不规则多边形与指定区域的位置关系，截取部分的实际形状不是必须得到的。所以，本文所述问题即可被等效为如何快速准确地判定矩形（星下点矩形）与不规则多边形（陆地区域）的位置关系问题。

对于矩形和不规则多边形的位置关系[2]如图1所示，分相交、外部和内部三种情况。所使用的算法必须能区分清楚这三种情况。

常用解决算法分两种[3]，一种是以Cohen-Sutherland算法为代表的直线段裁剪法，另一种是以Sutherland-Hodgman算法为代表的多边形裁剪法。

Cohen-Sutherland算法[4]首先将矩形区域四边所在直线延长，将整个平面分成9个区域并分别赋不同码值。然后根据组成多边形的各边端点所在位置对应码值，依次判断相邻线段与矩形的位置关系，最终得到多边形与矩形的位置关系。其弊端在于仅是孤立地处理被裁剪线段两端点，没有得到整根线段的整体信息，不可避免的会求取无效交点，降低运算效率[5]。并且如果需对多边形裁剪，需要将所有边等效为独立线段，经多次重复计算才可得到最终结果[6]。

针对上述缺陷，Sutherland-Hodgman算法是将多边形关于矩形的裁剪等效为多边形关于矩形四边所在直线的裁剪，此算法充分利用了线段与被裁剪多边形位置关系信息，没有无用运算，而且算法采用流水线方式执行，更易于硬件执行[7-8]。主要缺点在于只适用于凸多边形，如果是凹多边形，需要将其分解为多个凸多边形分别判断[9]。

根据实际应用，耀斑观测只需要矩形与多边形的位置关系信息，不需得到如果两者相交，交点连线截取部分的具体形状信息。上述两种算法[10]实现过程中都会进行交点求取计算，以便得到截取形状信息，增加数学计算量，降低了软件运行速度，与耀斑计算要求的实时性相悖[11]。为此，本文提出一种新算法，将矩形与多边形等效为多条线段，仅通过比较两者等效线段位置关系即可得到矩形与多边形的位置关系。

1 等效线段法

首先，将矩形区域和多边形区域分别离散为一组线段的集合。若仅使用离散的坐标点只能描述矩形与多边形边界而无法描述其内部区域。在这里期望将矩形边界及其内部区域均表示出来，所以采用在矩形区域内，选取间隔为1°的线段来等效矩形的方式描述矩形。等效结果如图2（a）所示，矩形区域被等效成一组（五根）等间距线段（竖直粗实线）的集合。

同理，代表海岸线地图的不规则多边形也可用此种方法分割成多条等效线段。针对给出的描述海岸线地图轮廓的数据，每个坐标点的经纬度分辨率为1°，如图2（b）所示，不规则多边形的轮廓用细实线描述。假设将多边形内部沿X轴方向分割，以粗直线AB所在的X轴坐标为例，将多边形内部沿Y轴方向分割成几个区域。粗直线与多边形内部的交点分别为C、D。分割的区域分别为AC、CD、DB。其中CD属于多边形内部，则在此X轴坐标下，线段CD用来描述多边形内部。这样，整个多边形内部就可用其X轴方向上，每个坐标值对应的Y轴方向分割线段的集合（不规则多边形内的细虚线）来描述。

图2（a）也描述了线段表述的多边形和矩形的位置关系，分别是包含（s2）、相交（s3）、不包含（s1）。从图中可以看出，判断多边形与矩形的位置关系，需要判断所有组成矩形的线段与对应X轴坐标下，所有组成多边形的线段的位置关系。线段的位置利用线段上下端点对应的Y轴坐标描述。判定途径有两种：1）如果矩形全部在多边形内部或者与其相交，即判定矩形不在或不全部在多边形外部；2）直接判定矩形与多边形内部无相交或包含成分。

矩形全部在多边形内部或者与其相交的情况分4种（如图3所示）[7]，AB虚线段为多边形描述线段，粗实线为矩形描述线段，两者均在同一X轴坐标下，这里为清晰可见而分开。依次描述的情况为：①多边形描述线段的下端点在矩形描述线段内部，上端点不在内部；②多边形描述线段的上端点在矩形描述线段的内部，下端点不在内部；③多边形描述线段的上下端点均在矩形描述线段的外部；④多边形描述线段的上下端点均在矩形描述线段内部。上述任一结果出现，说明矩形描述线段与多边形相交或者相互包含。

在依次判定比较每两根线段位置关系过程中，只要比较结果出现上述4种情况中任何一种，即可判定矩形不在多边形外部，即为包含或者相交的情况。

图3 矩形全部在多边形内部（或者与其相交）情况下的等效线段位置关系Fig.3 Location relation between equivalent lines

矩形与多边形内部无相交或包含成分的情况分为两种（如图4所示），依次描述的情况为：①多边形描述线段整体在矩形描述线段的上部；②多边形描述线段整体在矩形描述线段的下部。上述任一结果出现，只能说明该矩形描述线段全部在多边形外部。

在依次判定比较每两根线段位置关系过程中，必须将描述矩形区域线段集合的每一条线段与相应X坐标下，描述多边形区域的所有线段分别进行比较，结果只出现上述两种情况，才可判定矩形全部在多边形外部。

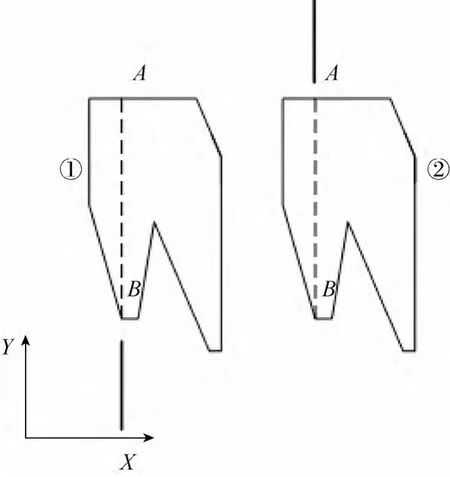
图4 矩形与多边形内部无相交（或包含）情况下的等效线段位置关系Fig.4 Location relation between lines

2 程序设计与实现

按照上述算法实现地图匹配，海岸线点坐标无需被依次存储，只需依次存储所有描述线段的上下端点坐标值即可。若按经度索引，纬度范围±90º，因此每个线段只需1byte空间，而按照纬度进行索引时，需存储线段上下端点经度值，经度范围±180º，每个线段需2byte存储空间。所以按经度索引可节省一半的存储空间，故而选用经度索引描述地图。

不同经度下的描述线段个数不同，这里为便于程序实现，记录所有经度下，描述线段数最多的个数作为所有经度的描述线段个数，这样任意经度对应的描述线段存储空间大小一致，便于程序处理。如果实际经度的描述线段较少，均填充90占位。因为实际矩形区域能够到达的区域纬度小于90°，故而判定结果必为：全在陆地区。

表1为地图数据存储结构。

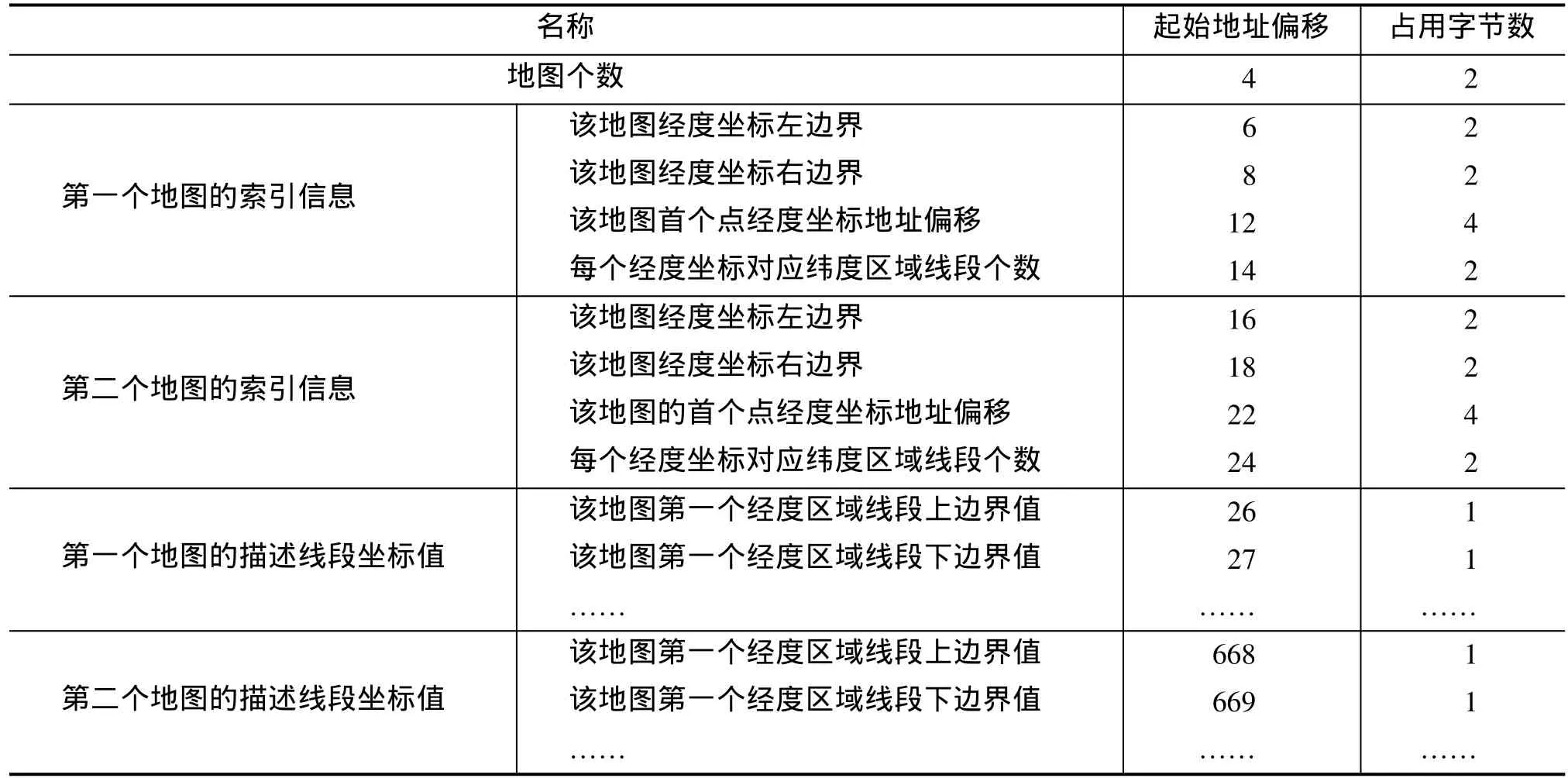
表1 等效线段法的地图数据存储结构Tab.1 Memory structure formap data of equivalent linesmethod

算法实现采用不全在海洋区域的判定途径，因为根据上文所述，此途径的比较次数较少，更加省时。上述四种情况的第三种可以归为第一种和第二种情况的组合，所以判断条件成立的情况减为三种。

为节约计算时间，首先判定矩形的经度跨度是否在地图的经度跨度区间内。另外，假设实际卫星所能运行到的纬度区域确定（实际为±60°），如果矩形超出此区域，不进行耀斑计算，设为进入陆地区。具体计算流程如图5所示。

图5 等效线段法流程Fig.5 Flow chartof equivalent linesmethod

此算法的核心部分在于三种情况的判断，即比较矩形描述线段上下端点的坐标值（yt，yb）与地图描述线段上下端点坐标（YT，YB）的大小关系：1）YBYT，且yb

首幅地图判定完毕后，如果矩形判定为在“海洋区”，即可结束判断流程。否则调入第二幅地图数据，重新进行计算流程，判断是否落入第二幅地图的“海洋区”。从而最终确定矩形与海岸线地图的位置关系。

3 实验结果分析

根据工程需要，软件需快速地判断出卫星能否进行耀斑计算，并执行相应的动作。判断时间过长会影响卫星进行耀斑观测的准确度。为此，通过表2来对上述三种算法判定时间进行总结[12-13]。

表2 三种算法实现的计算量比较Tab.1 The comparison of calculation amountbetween the threemethod

为了比较3种算法的执行时间，这里首先给出实际海岸线地图与星下点矩形的基本信息，并按每种算法的计算量最大时所用时间进行比较，图6为海岸线地图实际形状。

图6 地球指定区域海岸线地图Fig.6 Coast linemap of the certain earth area

实际组成地图的线段个数为881条，不规则排列并依次首尾衔接，两条线段衔接点坐标均为整数经纬度，同一经度对应的纬度描述线段最多3条。实际要求的星下点矩形经度跨度11°，纬度跨度2°。星下点矩形的位置完全由卫星的运行轨迹确认，由于每轨轨迹均不相同，默认星下点能够覆盖海岸线地图的所有地方。当矩形中心点坐标为（91°，22°）时，出现与地图交点个数最多情况（共7个交点，上边、下边、右边各2个，左边1个），表3的相交时间即利用此时矩形位置计算。

算法使用80c32单片机利用C语言编写，12MHz外部钟频。表3给出了矩形与地图相交、在地图内部、外部时，三种算法各自的执行时间。等效线段法在实际使用中，无需准确区分内部与相交，只要确认其位置关系为其中之一。如文章第二节所述，只需区分矩形在陆地区或在海洋区，这使得计算时间可以进一步减小。

表3 三种算法实现的计算时间比较Tab.3 Comparison of calculation time between the threemethods s

由表3结果可以看出，Cohen-Sutherland算法与Sutherland-Hodgman算法将大量的时间用于求取矩形与地图交点，因为两种算法均需利用交点求取裁剪线段形状[14]，但这并不是实际必需要求实现的，而且关于线段间位置的判断均多于地图线段组成数量。等效线段法无需求取交点，且判断次数很少，根据实际矩形与地图描述线段组成个数，当位置关系为外部和内部时，需要判断33次；相交则最多需要判断33次，即最大判断次数为矩形经度坐标跨度与海岸线地图纬度描述线段个数之积（如果判断过程中已经确定相交位置关系，终止判断）。由上述分析可知，等效线段法仅有少量的判断次数，实现更为快速，因此更能满足耀斑观测的实时快速要求。

等效线段法的地图数据总存储空间（1 766 byte）远小于直接存储地图坐标点的存储空间（2 643 byte），原因是坐标点存储法中每个纬度需要1 byte存储空间，经度需要2 byte，而等效线段法的坐标点均只需1 byte；程序代码方面上述三种算法占用空间大小近似，均在1kbyte左右。综上比较，等效线段法内存消耗更小。

等效线段法的计算精度完全取决于海岸线地图描述坐标的分辨率。星下点矩形的大小固定，中心由卫星的位置实时确定。由于实际工程中，地图的最小分辨率为1°，当卫星星下点经度坐标出现小数时，必须对其取整，以便星下点矩形描述线段能够和海岸线地图描述线段在经度坐标上一一对应。所以，求得的星下点经度必须进行四舍五入，等效线段法的计算精度会因此下降。当星下点矩形处于海岸线地图边界时，可能导致两者位置关系判断结果与实际不符。但是，可以通过提高海岸线地图坐标的分辨率来提高判读精度，因此消耗的额外计算量与地图坐标分辨率成正比增长。由表1可知，Cohen-Sutherland算法与Sutherland-Hodgman算法的计算量与地图坐标的分辨率也是成正比增长的，所以等效线段法仍具有实时快速的优点。经验证，1°的经纬度分辨率已能满足工程需要，无需再提高地图坐标分辨率。

4 结论

为了准确快速地判定耀斑观测能否进行，本文提出了一种新的算法——等效线段法，并且给出了具体原理与软件实现流程。通过实践证明，该算法因无需得出截取图形形状，而避免了交点求取计算，仅需少量次数的数值大小比较就可得到卫星视场与海洋位置关系，能够更加快速地判断耀斑观测条件是否满足，而且占用较少的软件资源。

（References）

[1] 唐云,罗俊松.计算机图形技术在数据计算方面的应用[J].制造业自动化,2010,32(11):198.TANG Yun,LUO Junsong.Application of Computer Graphics Technology in Data of Computation[J].Manufacturing Automation,2010,32(11):198.(in Chinese)

[2] New ManW M,Sproull R F.Principals of Interactive Computer Graphics[M].M cGraw-Hill New York,1979.

[3] 彭欢,陆国栋,谭建荣.基于端点与交点编码的矩形窗口多边形裁剪新算法[J].工程图学学报,2006,27(4):72-76.PENG Huan,LU Guodong,TAN Jianrong.A New Algorithm of Polygon Clipping Against RectangularWindow Based on the Endpointand Intersection-point Encoding[J].Manufacturing Automation,2006,27(4):72-76.(in Chinese)

[4] 孔德慧,尹宝才,刘媛媛.对Cohen-Sutherland线段裁剪算法的改进[J].北京工业大学学报,2002,28(4):483.KONG Dehui,YIN Baocai,LIU Yuanyuan.Improvement in the Algorithm of Cohen-surtherland Segment Clipping[J].Journalof Beijing Polytechnic University,2002,28(4):483.(in Chinese)

[5] 严圣华.二维线段裁剪C-S算法的分析与改进[C].全国第21届计算机技术与应用学术会议,2010.YAN Shenghua.The Improvement and Analysis of the Cohen-Sutherland Clipping Method[C].The 21st Computer Technology and Application Conference,2010.(in Chinese)

[6] 任洪海.一种基于直线区域划分的线段裁剪算法[J].科学技术与工程,2008,8(13):3677.REN Honghai.Line Clipping Algorithm Based on Line Region-subdivision[J].Science Technology and Engineering,2008,8(13):3677.(in Chinese)

[7] Liang Y D,Barsky BA.An Analysis and Algorithm for Polygon Clipping[J].CACM,1983(26):11.

[8] 李建胜,张韶华,范东娟.一种基于线性求解的多边形图像裁剪方法[J].计算机工程与应用,2008,39(6):170.LIJiansheng,ZHANG Shaohua,FAN Dongjuan.An Algorithm of Polygon Clipping Based on the Linear Solve Method[J].Computer Engineering and Applications,2008,39(6):170.(in Chinese)

[9] 王世萍,王志强.多边形裁剪通用算法[J].工程图学学报,1995,16(1):42-47.WANG Shiping,WANG Zhiqiang.A General Algorithm of the Polygon Clipping[J].Manufacturing Automation,1995,16(1):42-47.(in Chinese)

[10] 彭妮娜,王琨,李涛.地表双向反射特性对遥感图像的影响分析[J].航天返回与遥感,2011,32(4):45.PENG Nina,WANG Kun,LI Tao.Research of BRDF Effects on Remote Sensing Imagery[J].Spacecraft Recovery&Remote Sensing,2011,32(4):45.(in Chinese)

[11] Creiner G,Hormann K.EfficientClipping of Arbitrary Polygons[J].ACM Transactions on Graphics,1998,17(2):71-83.

[12] 张以成,冯西权.线段二维裁剪与绘制的算法性能分析[J].计算机工程与应用,2013,49(6):170.ZHANG Yicheng,FENG Xiquan.Performance Analysis on Line Two-dimensional Clipping and Draw ing Algorithm[J].Computer Engineering and Applications,2013,49(6):170.(in Chinese)

[13] 欧中亚.计算机图形学中二维裁剪算法的研究[J].中小企业管理与科技(上旬刊),2011(22):288-289.OU Zhongya.The Study of 2-D Clipping Algorithm Computer Graphics Technology[J].Management&Technology of SMEs,2011(22):288-289.(in Chinese)

[14] 徐洪学.二维有向直线段常用裁剪算法裁剪效率比较[J].微型电脑应用,1999(7):35.XU Hongxue.The Efficiency Comparison among the General Methods for 2-D Line Clipping[J].M icrocomputer Application,1999(7):35.(in Chinese)

[15] Southerland IE.AClipping Divider[M].FJCC,Thompson Books,Washington D.C,1968.