隧道型钢喷混凝土初期支护的可靠度计算方法及应用

黄逸群，林从谋，黄清祥，林大炜，孟希

（华侨大学 岩土工程研究所，福建 厦门361021）

隧道的塌方是隧道施工中比较常见和典型的事故，而且一旦发生事故，对机械设备及施工人员所造成的损失往往是巨大的.隧道的初期支护作为紧贴围岩的结构，在它们的共同作用下，围岩的整体稳定性是可以通过围岩周边位移测量值及其速率的变化综合反映出来的［1］.因此，隧道初期支护的安全性是隧道施工中所重点关心的问题.为了确保施工期间隧道的安全，初期支护的安全性评价是实现隧道动态设计的关键因素，相关的研究也取得了较多成果［2-7］.如杨成永等［2］首次提出通过初期支护监测数据得到初期支护内力并计算可靠度的“位移法”；文献［3］在“位移法”的基础上提出了格栅钢架喷混凝土支护的功能函数，通过可靠度的计算评价了格栅钢架喷混凝土支护的安全性；文献［4］运用可靠度理论分析洞顶松散土体的塌方概率，并对影响参数进行了敏感性分析；文献［5］建立了隧道扩建施工过程的有限元模型，研究CD工法开挖时软弱围岩的稳定性，并将数值计算结果同现场量测值进行了对比分析；文献［6］构建了考虑综合安全系数的隧道初期支护功能函数，利用“宽界限法”对隧道衬砌结构的体系进行分析，并计算了隧道初期支护的体系可靠度；文献［7］通过监测数据反演围岩力学参数，通过数值模拟建立了型钢喷射混凝土安全性评价的数值计算方法.然而，无论是可靠度计算的评价方法还是安全系数的评价方法，对于隧道的下一步施工都能起到准确的指导效果.本文在已有研究的基础上，针对隧道型钢喷混凝土初期支护的截面失效，提出了隧道型钢喷混凝土初期支护的截面失效的功能函数；然后结合工程实例，利用此功能函数对该隧道型钢喷混凝土初期支护进行可靠度计算及安全性评价.

1 结构的功能函数与初期支护内力的计算方法

1.1 结构的功能函数

针对隧道型钢喷混凝土初期支护的截面失效问题，参考JGJ 138-2001《型钢混凝土组合结构技术规程》［8］及JTG D70-2004《公路隧道设计规范》［9］中相关公式，把型钢喷混凝土初期支护看成是偏心受压构件，基于平截面假定，忽略纵向连接筋对初期支护内力的影响，提出受压和受弯的功能函数，即

式（1），（2）中：Zc，Zm分别为受压和受弯的功能函数；fc为混凝土轴心抗压强度设计值；b为截面宽度；x为受压区高度；h0为型钢翼缘受拉边作用点至混凝土受压边缘的距离；a′a为型钢翼缘受压边重心至混凝土截面近边的距离；f′a为型钢的抗压强度设计值；A′af和Aaf为型钢受压和受拉翼缘的面积；σa型钢翼缘受拉边应力；Naw和Maw为型钢腹板承受的轴向合力和力矩；N和M为初期支护的轴力和弯矩.

图1 初期支护偏心受压示意图Fig.1 Eccentric compression on primary lining

1.2 型钢腹板承受的轴向合力的计算

式（3），（4）中：δ1和δ2分别为型钢腹板上、下端至截面上边的距离与h0的比值；ξ和ξb分别为相对受压区高度和相对界限受压区高度；tw为型钢腹板的厚度.

计算时，先假设构件为大偏心受压，求出受压区高度x.若满足大偏心受压条件，则代入大偏心受压型钢腹板承受的轴向合力公式进行计算；若不满足则为小偏心受压，重新求出受压区高度x，再进行计算.图2为型钢腹板承受的轴向合力计算流程图.

图2 型钢腹板承受的轴向合力计算流程图Fig.2 Axial force calculation flow chart of shape steel web plate

1.3 初期支护内力的计算方法

隧道初期支护内力有如下3种计算方法.

1）假定抗力图形法 .假定抗力区范围及抗力分布规律，按超静定结构求解衬砌内力.

2）弹性地基梁法 .将衬砌结构看成是置于弹性地基上的曲梁或直梁，弹性地基上抗力按温克尔假定的局部变形理论求解.

3）弹性链杆法 .将衬砌与围岩所组成的衬砌结构体系离散化为有限个衬砌单元和弹性支承单元所组成的组合体，并以此来计算的有限元计算法.

上述计算方法是以“荷载-结构”模型通过衬砌的荷载来计算其内力，然而，新奥法隧道无法通过荷载计算衬砌内力［2］，且上述方法计算繁琐.因此，采用杨成永提出的位移法［2］来计算轴力和弯矩的.即

式（5）中：ΔNi为第i次测量时的轴力增量；ΔMi为第i次测量时的弯矩增量；ε为从第i-1次到i次测量时初期支护中轴的应变增量，ε＝（Li-Li-1）／Li-1，Li为第i次测量时初期支护弧段中轴的长度；I为截面的惯性矩；ρi为第i次测量时初期支护弧段内表面的曲率半径.

图3为初期支护弧段的计算简图.初期支护弧段的曲率半径与中轴长度可以通过拱高H和拱宽D来表征，但不同的弧段拟合曲线会影响曲率半径的计算及最后可靠指标的计算 .文献［10］研究了不同拟合曲线对可靠指标的计算的影响，得到抛物线与实际情况符合最好的结论，因此，文中也选用抛物线来进行拟合，即

图3 初期支护弧段的计算简图Fig.3 Calculation diagram of primary lining arcs

对于式（5）中混凝土的弹性模量Ei，为了考虑型钢拱架、系统锚杆、钢筋网对可靠指标计算的影响，拟采用等效的方法［11］，即把型钢拱架、系统锚杆、钢筋网的弹性模量折算到混凝土中.即有

式（8）中：Ei和E0分别为折算后和折算前的混凝土弹性模量；Eg和Ag为型刚拱架的弹性模量和截面面积；Em和Am为系统锚杆的弹性模量和截面面积；Ew和Aw为钢筋网的弹性模量和截面面积；A0为混凝土的截面面积.

2 可靠度计算中参数的不确定性及计算方法

2.1 混凝土强度参数的不确定性

混凝土的抗压和抗拉强度随着时间的变化对初期支护失效概率的计算影响较大.文献［12］给出了采用负指数拟合混凝土强度随时间增长的方法，即

式（9）中：fc，t，ft，t和E0，t分别为t时刻混凝土的抗压强度、抗拉强度和弹性模量；fc，∞，ft，∞和f0，∞分别为混凝土的极限抗压强度、极限抗拉强度和极限弹性模量；α，β和γ为时间参数，都取经验值0.015；时间t的单位为小时.t时刻混凝土的抗压强度、抗拉强度和弹性模量3个参数的变异系数可按文献［2］的取法，都取0.15，均为正态分布.

2.2 型钢拱架强度参数的不确定性

型钢拱架的抗压、抗拉强度、截面面积和弹性模量的不确定性参考文献［3］的取值.即型钢拱架的抗压、抗拉强度均值取340 MPa，变异系数为0.08；型钢拱架的截面面积均值按设计值取，变异系数为0.03；型钢拱架的弹性模量均值为200 GPa，变异系数为0.08，均为正态分布.

2.3 拱高H和拱宽D及支护厚度h的不确定性

由文献［2］可知：拱高测量误差均值为0 mm，标准差为0.812 mm；拱宽测量误差均值为0 mm，标准差为0.74 mm；支护厚度在Ⅴ级围岩下的均值按设计值取值，变异系数为0.09，均为正态分布.

2.4 蒙特卡罗模拟法

蒙特卡罗模拟法首先对随机变量进行大量随机抽样，然后把这些抽样值一组一组地代入功能函数中，确定结构的失效与否，最后用结构失效次数占总抽样数作为结构的失效概率.该方法概念明确且计算所得到的失效概率精度高.

利用提出的功能函数及各随机变量的概率特征，考虑上述优点，采用蒙特卡罗模拟法，基于Matlab编制程序进行失效概率计算，并换算为可靠指标 .为使结果更加精确，每个数据模拟次数达到107.

3 实例验算

江家渡隧道位于宁武高速公路宁德段，隧道右线起讫桩号为YK31＋640～YK32＋565，全长925 m.断面YK32＋235围岩类别为V级，初期支护混凝土设计厚度为24 cm，采用C25混凝土，型钢拱架为I18，截面面积为30.6 cm2.初期支护的施作时间为2010年6月30日，监测断面安装日期为2010年7月3日，通过对监测数据的换算，初始拱宽为11 344.56 mm，初始拱高为4 556.34 mm.该断面不同时刻、不同拱高和拱宽及计算所得的失效概率、可靠指标，如表1所示.

表1 江家渡隧道YK32＋235可靠指标计算结果Tab.1 Reliability index calculation results of Jiangjiadu tunnel at section YK32＋235

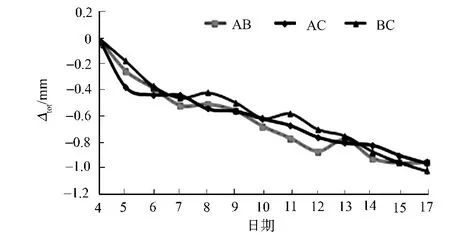
图4 YK32＋235初衬周边位移曲线图Fig.4 Surrounding displacement curve of section YK32＋235

图5 YK32＋235初衬拱顶下沉曲线图 Fig.5 Vault settlement curve of section YK32＋235

图4，5为该隧道YK32＋235断面在测试日期（2010年7月4-17日）的实测周边位移和拱顶下沉曲线图 .图4，5中：Δtot，Stot为周边位移和拱顶下沉的累计值；ABC为隧道进行周边收敛监测所布置的监测点；G1，G2，G3是拱顶下沉监测点.

从图4，5可知：该隧道断面的周边位移和拱顶下沉变形量都较小，周边位移和拱顶下沉的变形速率分别为0.083，0.130 mm·d-1，均小于相关规定的数值，说明该隧道断面处于稳定状态.

从表1可知：江家渡隧道断面YK32＋235的初期支护弧段的失效概率较低，与实际该隧道断面所处的正常稳定状态相吻合 .隧道初期支护的失效概率随着时间的变化略有起伏，主要与拱宽和拱高变形量的大小的有关，一天的时间变形量大，则失效概率变大，变形量小，则失效概率变小，但总体仍然在可接受的范围.隧道初期支护可靠指标随时间的变化也是有所起伏，与拱宽和拱高变形量大小相对应，而且符合我国现行规范［13］对可靠指标的规定.

4 结束语

文中针对型钢喷混凝土初期支护隧道的可靠度进行计算分析，提出了初期支护截面失效的功能函数；通过对比初期支护内力的不同计算方法，讨论了混凝土强度和型钢拱架的变异性 .最后针对一个实际隧道工程进行了验算，结果表明计算结果与实际状态相吻合，说明计算方法是合理有效的.然而，文中的研究也存在不足之处，如随机变量相关的统计参数还不完善，不能很好的反映实际变量的概率特征，未考虑的参数变量对可靠度的敏感性分析等.这些内容都有待进一步研究.

［1］ 牟瑞芳.论隧道工程围岩稳定性及其可控制性［J］.铁道学报，1996，18（4）：82-88.

［2］ 杨成永，张弥，白小亮.隧道喷混凝土衬砌结构可靠度分析的位移方法［J］.岩石力学与工程学报，2003，2（2）：266-269.

［3］ 李洪泉，杨成永，徐明新，等.隧道格栅钢架喷混凝土支护安全性评价［J］.岩石力学与工程学报，2009，28（2）：3903-3908.

［4］ 黄志波，林从谋，陈莹，等.隧道洞口土体塌方的可靠度分析［J］.华侨大学学报：自然科学版，2012，33（5）：557-560.

［5］ 林从谋，张在晨，郑强，等.小净距隧道原位二扩四CD工法软弱围岩稳定性及支护参数研究［J］.土木工程学报，2013，46（7）：124-132.

［6］ 朱彦鹏，陈思阳，欧华方，等.隧道初期衬砌支护系统的可靠度分析［J］.兰州理工大学学报，2011，37（4）：125-129.

［7］ 徐帮树，杨为民，王者超，等.公路隧道型钢喷射混凝土初期支护安全评价研究［J］.岩土力学，2012，33（1）：248-252.

［8］ 中华人民共和国行业标准编写组.JGJ 138-2001型钢混凝土组合结构技术规程［S］.北京：中国建筑工业出版社，2001：25-26.

［9］ 中华人民共和国行业标准编写组.JTG D70-2004公路隧道设计规范［S］.北京：人民交通出版社，2004：41-44.

［10］ 谢圣娴，杨成永，杨菁轩.不同拟合曲线对结构可靠度分析位移方法的适应性［J］.北方交通大学学报，2003，27（1）：84-86.

［11］ 李术才，朱维申，陈卫忠，等.弹塑性大位移有限元方法在软岩隧道变形预估系统研究中的应用［J］.岩石力学与工程学报，2002，21（4）：466-470.

［12］ ORESTE PP.A procedure for determining the reaction curve of shotcrete lining considering transient conditions［J］.Rock Mechanics and Rock Engineering，2003，36（3）：209-236.

［13］ 中华人民共和国住房和城乡建设部.GB 50153-2008工程结构可靠性设计统一标准［S］.北京：中国建筑工业出版社，2008：32-33.