Some Notes on Normality Criteria of Meromorphic Functions
2014-03-03,*
,*
(1.School of Mathematics Science,Xinjiang Normal University,Urumqi,830054)
(2.School of Mathematics and Information Sciences,Guangzhou University, Guangzhou,510006)
Some Notes on Normality Criteria of Meromorphic Functions
CHEN WEI1,ZHANG YING-YING1,TIAN HONG-GEN1,*AND YUAN WEN-JUN2
(1.School of Mathematics Science,Xinjiang Normal University,Urumqi,830054)
(2.School of Mathematics and Information Sciences,Guangzhou University, Guangzhou,510006)
Communicated by Ji You-qing
In this paper,we study the normality of families of meromorohic functions related to a Hayman conjecture.We prove that the conditions in Hayman conjecture and in other criterions can be relaxed.The results in this paper improve some previous results.
meromorphic function,shared value,normal criterion
1 Introduction and Main Results
We use C to denote the open complex plane,(=C∪{∞})to denote the extended complex plane and D to denote a domain in C.A family F of meromorphic functions de fi ned in D⊂C is said to be normal,if any sequence{fn}⊂F contains a subsequence which converges spherically,and locally,uniformly in D to a meromorphic function or∞. Clearly,F is said to be normal in D if and only if it is normal at every point in D(see[1]).
Let D be a domain in C,f and g be two meromorphic functions,a and b be complex numbers.If g(z)=b whenever f(z)=a,we write
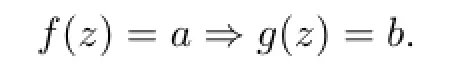
If f(z)=a⇒g(z)=b and g(z)=b⇒f(z)=a,we write
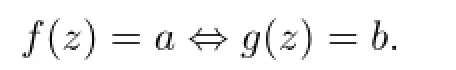
According to Bloch’s principle(see[2]),every condition which reduces a meromorphic function in the plane C to a constant forces a family of meromorphic functions in a domain D normal.Although the principle is false in general(see[3]),many authors proved normality criterion for families of meromorphic functions by starting from Liouville-Picard type theorem(see[4]).Moreover,it is interesting to fi nd normality criteria from the point of view of shared values.Schwick[5]fi rst proved an interesting result that a family of meromorphic functions in a domain is normal if every function in that family shares three distinct fi nite complex numbers with its fi rst derivative.And later,more results about normality criteria concerning shared values have emerged.In recent years,this subject has attracted the attention of many researchers worldwide.
In this paper,we use σ(x,y)to denote the spherical distance between x and y and the de fi nition of the spherical distance can be found in[6].

In 2004,Singh A P and Singh A[8]proved that the condition for the constants in Theorem 1.1 to be the same for all f∈F can be relaxed to some extent,and they proved the following theorem.
Theorem 1.2[8]LetFbe a family of meromorphic functions in the unit disc Δ.For eachf∈F,suppose that there exist nonzero complex numbersbf,cfsatisfying:
(ii)min{σ(0,bf),σ(0,cf),σ(bf,cf)}≥mfor somem>0;
ThenFis normal in Δ.
Theorem 1.3[9]LetFbe a family of holomorphic(meromorphic)functions in a domainD,n∈N,a=0,andb∈C.If−̸=bfor each functionf∈Fandn≥2 (n≥3),thenFis normal inD.
From the idea of Theorem 1.2,we generalize Theorem 1.3 as the following theorem.
Theorem 1.4(Main Theorem I)LetFbe a family of meromorphic functions in the unit disc Δ,andn(≥3)be a positive integer.For everyf∈F,there exist fi nite nonzero complex numbersbf,cfdepending onfsatisfying:
ThenFis normal in Δ.is a constant;
(ii)min{σ(0,bf),σ(0,cf),σ(bf,cf)}≥mfor somem>0;
(iii)
Theorem 1.5[10]LetFbe a family of meromorphic functions in a domainD,anda(̸=0),bbe two fi nite constants.De fi ne
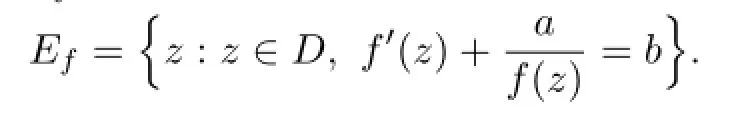
If there exists a positive numberMsuch that for everyf∈F,|f(z)|≥Mwheneverz∈Ef, thenFis normal.
Theorem 1.6[11]LetFbe a family of meromorphic functions inD,nbe a positive integer, anda,bbe two fi nite complex numbers such thata=0.If for each functionf∈F,f′−af−n̸=b,thenFis normal inD.
Theorem 1.7(Main Theorem II)LetFbe a family of meromorphic functions in the unit disc Δ,andnbe a positive integer.For everyf∈F,there exist fi nite nonzero complex numbersbf,cfdepending onfsatisfying:
ThenFis normal in Δ.
In 2009,Charak and Rieppo[12]generalized Theorem 1.5 and obtained two normality criteria of Lahiri’s type.
Theorem 1.8[12]LetFbe a family of meromorphic functions in a domainD.Leta,b∈Cwitha=0.Letm1,m2,n1,n2be nonnegative integers such that
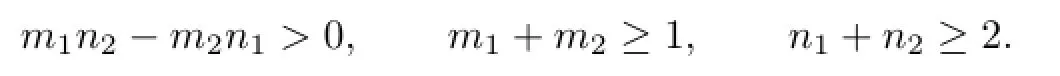
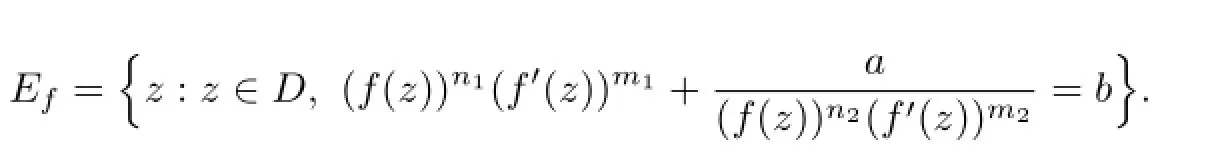
Putis a constant;
(ii)min{σ(0,bf),σ(0,cf),σ(bf,cf)}≥mfor somem>0;
(iii)
If there exists a positive constantMsuch that|f(z)|≥Mfor allf∈Fwheneverz∈Ef, thenFis a normal family.
Theorem 1.9[12]LetFbe a family of meromorphic functions in a domainD.Leta,b∈Cwitha=0.Letm1,m2,n1,n2be nonnegative integers such thatm1n2=m2n1>0,and put
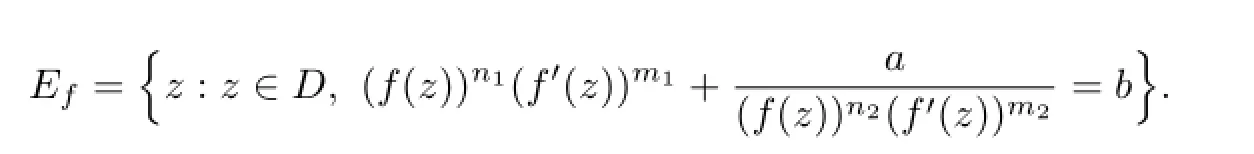
If there exists a positive constantMsuch that|f(z)|≥Mfor allf∈Fwheneverz∈Ef, thenFis a normal family.
In this paper,we also obtain the following results.
Theorem 1.10(Main Theorem III)LetFbe a family of meromorphic functions in the unit disc Δ,andm1,m2,n1,n2be nonnegative integers such thatm1n2−m2n1> 0, m1+m2≥1,andn1+n2≥2.For everyf∈F,there exist fi nite nonzero complex numbersbf,cfdepending onfsatisfying:
(ii)min{σ(0,bf),σ(0,cf),σ(bf,cf)}≥mfor somem>0;
wheres=n1+m1,t=n2+m2.
ThenFis normal in Δ.
Theorem 1.11(Main Theorem IV)LetFbe a family of meromorphic functions in a domainD,andm1,m2,n1,n2be nonnegative integers such thatm1n2=m2n1>0.For everyf∈F,there exist fi nite nonzero complex numbersbf,cfdepending onfsatisfying:
(ii)min{σ(0,bf),σ(0,cf),σ(bf,cf)}≥mfor somem>0;
wheres=n1+m1,t=n2+m2.
ThenFis normal in Δ.
2 Some Lemmas
In order to prove our theorems,we require the following results.
Lemma 2.1[7,13]LetFbe a family of meromorphic functions in a domain D,andkbe a positive integer,such that each functionf∈Fhas only zeros of multiplicity at leastk,and suppose there exists anA≥1such that≤Awheneverf(z)=0,f∈F.IfFis not normal atz0∈D,then for each0≤α≤k,there exist a sequence of pointszn∈Dwithzn→z0,a sequence of positive numbersρn→0+,and a subsequence of functionsfn∈Fsuch that
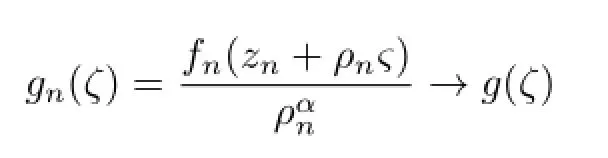
locally uniformly with respect to the spherical metric inC,wheregis a nonconstant meromorphic function,all of whose zeros have multiplicity at leastk,such thatg♯(ζ)≤g♯(0)=kA+1. Moreover,ghas order at most2.
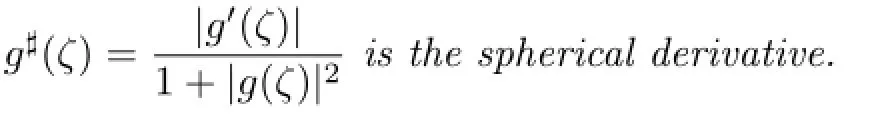
Lemma 2.2[6]Letmbe any positive number.Then,a M¨obius transformationgsatisfyingσ(g(a),g(b))≥m,σ(g(b),g(c))≥m,σ(g(c),g(a))≥mfor some constantsa,bandc,also satis fi es the uniform Lipschitz condition
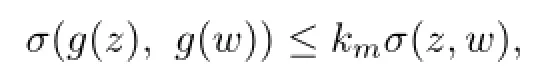
wherekmis a constant depending onm.
Lemma 2.3[14]Letfbe a meromorphic function inC,nbe a positive integer,andbbe a non-zero constant.Iffnf′̸=b,thenfis a constant.Moreover,iffis a transcendental function,thenfnf′assumes every fi nite non-zero value in fi nitely often.
Lemma 2.4Letfbe a nonconstant meromorphic function inC,anda=0be a fi nite complex number.Then for any positive integern≥3,has least one zero.
Proof.If0,thenwhere c is a constant.This contradicts that f is a meromorphic function since n≥3.
If f′−afn0,thenThen−a.By Lemma 2.3,φ is a constant,and so f is a constant which contradicts that f is a nonconstant.Hence,f′−afnhas least one zero.
Lemma 2.5[15]Take nonnegative integersn,n1,···,nkwithn≥1,n1+n2+···+ nk≥1and de fi ned=n+n1+n2+···+nk.Letfbe a transcendental meromorphic function with the de fi ciency Δ(0,f)>a.SetThen for any nonzero valuec,the function−chas in fi nitely many zeros.
Lemma 2.6[12]Letfbe a nonconstant rational function,andm,nbe natural numbers. Then,the functiontakes every fi nite nonzero valuea∈C.
Lemma 2.7[12]Leta,b∈Cwitha=0,andfbe a nonconstant meromorphic function. Ifm1,m2,n1,n2are positive integers such thatm1n2=m2n1,then
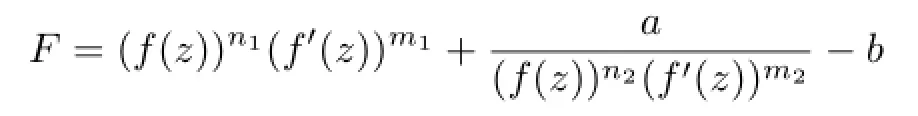
has a fi nite zero.
3 Proof of the Theorems
Proof of Theorem 1.4Let M=We can fi nd nonzero constants b and c satisfying M=For each f∈F,de fi ne a M¨obius map gfby gf=Then
By Lemma 2.4,there exists a ξ0such that

Note that
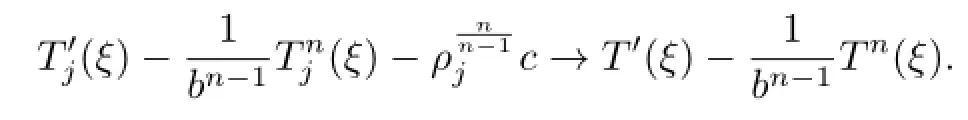
By Hurwitz’s Theorem,there exists a sequence of points ξj→ ξ0such that(for j large enough)
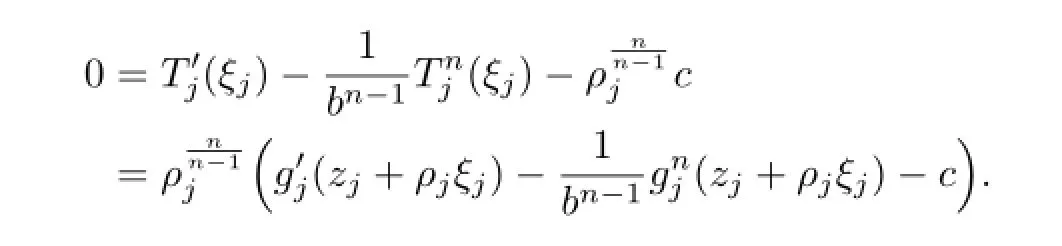
Hence
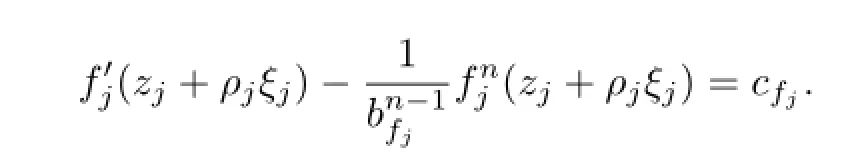
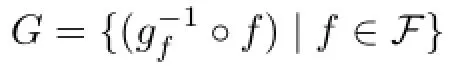
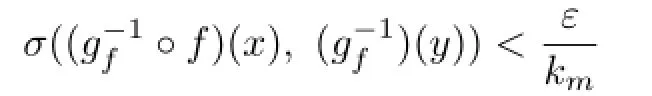
for each f∈F.By Lemma 2.2,we get
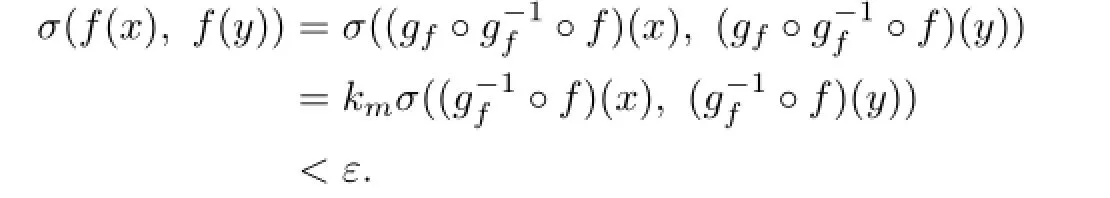
Therefore,the family is equicontinuous inΔ.This completes the proof of Theorem 1.4.
Proof of Theorem 1.7Let MWe can fi nd nonzero constants b and c satisfying M=For each f∈F,de fi ne a M¨obius map gf
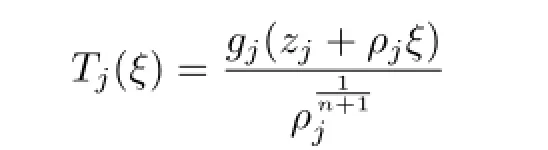
converges locally uniformly with respect to the spherical metric to a nonconstant meromorphic function T(ξ)whose spherical derivative is limited and T has order at most 2.
By Lemma 2.3,we get
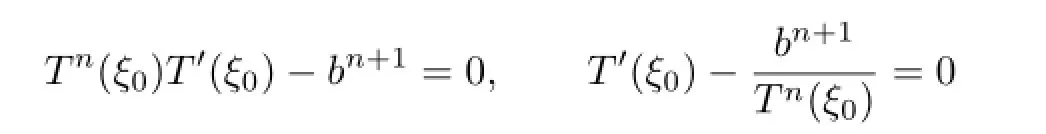
for some ξ0∈C.Clearly,ξ0is neither a zero nor a pole of T(ξ).Note that
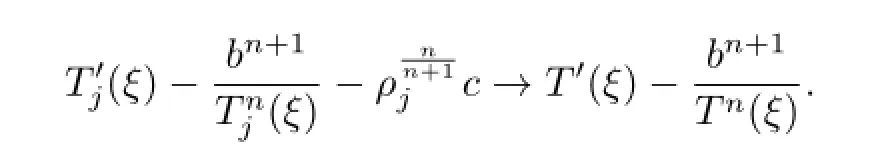
By Hurwitz’s Theorem,there exists a sequence of points ξj→ ξ0such that(for j large enough)
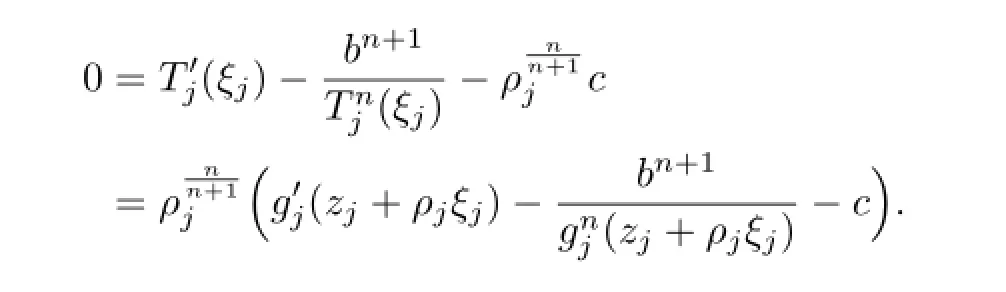
Hence
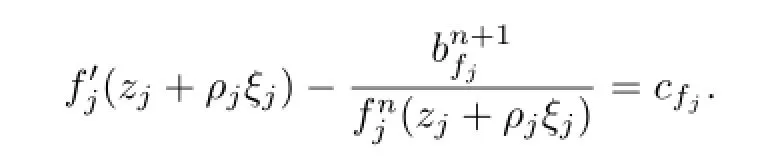
So we have|fj(zj+ρjξj)|≥|bfj|,by the condition
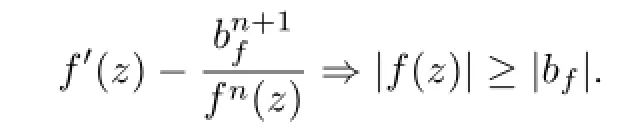
Thus
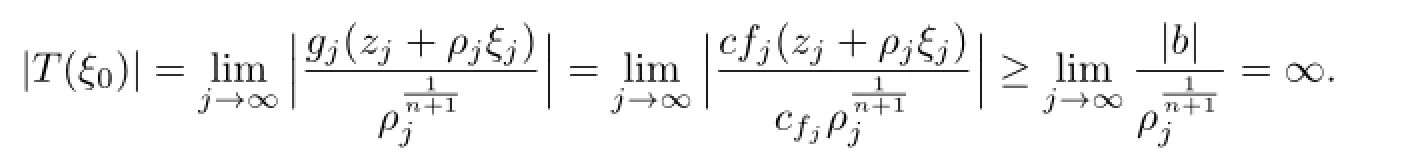
So ξ0is a pole of T(ξ),a contradiction.Hence G=is normal and equicontinuous inΔ.Then givenwhere kmis the constant of Lemma 2.2,there exists aΔ>0 such that for the spherical distance σ(x,y)<Δ,

for each f∈F.Hence,by Lemma 2.2,
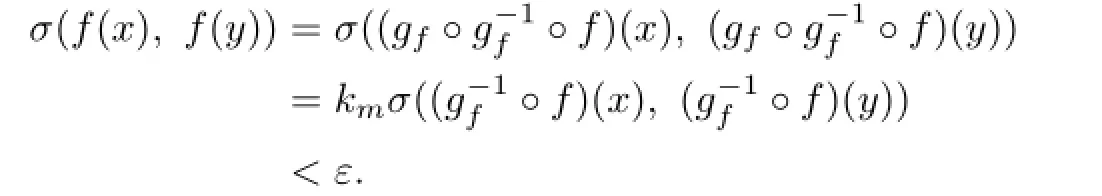
Therefore,the family is equicontinuous inΔ.This completes the proof of Theorem 1.7.
Proof of Theorem 1.10Let MWe can fi nd nonzero constants b and c satisfying M=For each f∈F,de fi ne a M¨obius map gfby gf=and thus
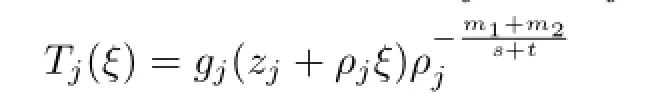
converges locally uniformly with respect to the spherical metric to a nonconstant meromorphic function T(ξ)whose spherical derivate is limited and T has order at most 2.By Lemmas 2.5 and 2.6,we obtain
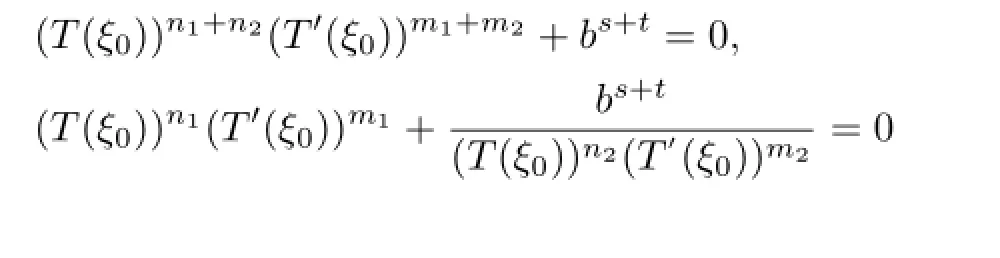
for some ξ0∈C.Clearly,ξ0is neither a zero nor a pole of T(ξ).Note
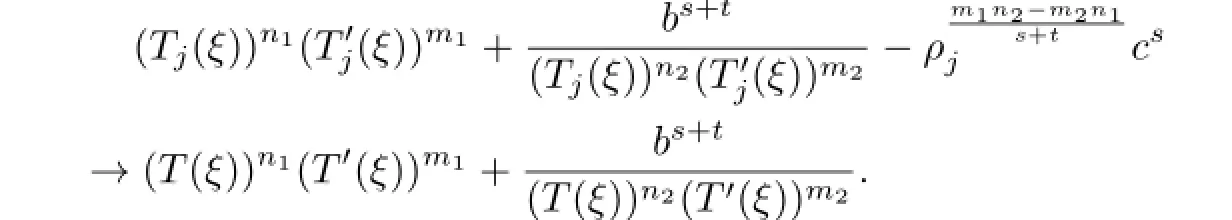
By Hurwitz’s Theorem,there exists a sequence of points ξj→ ξ0such that(for j large enough)
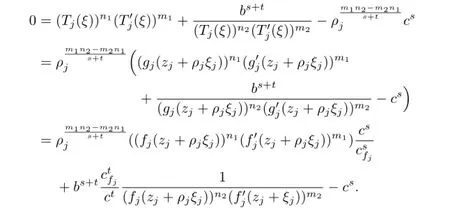
Hence
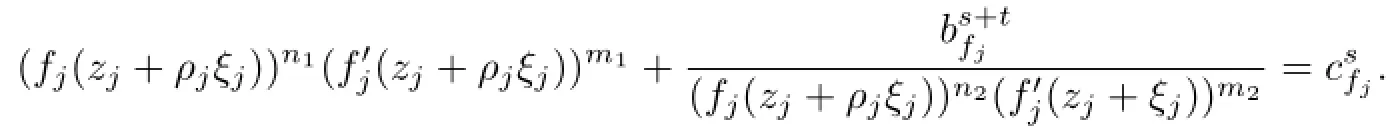
So we have|fj(zj+ρjξj)|≥|bfj|by the condition

Thus
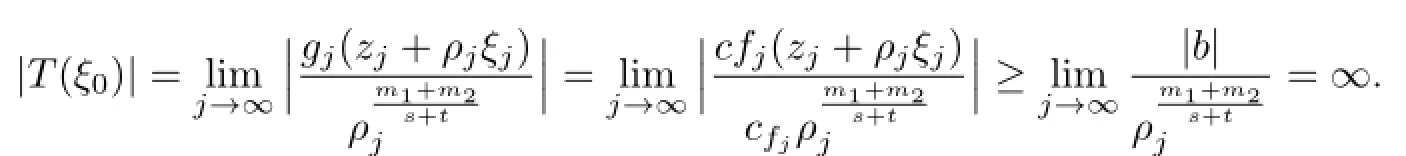
So ξ0is a pole of T(ξ),a contradiction.Hence G=is normal and equicontinuous inΔ.Then given>0,where kmis the constant of Lemma 2.2,there exists aΔ>0 such that for the spherical distance σ(x,y)<Δ,one has
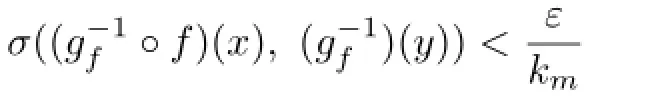
for each f∈F.Hence by Lemma 2.2.
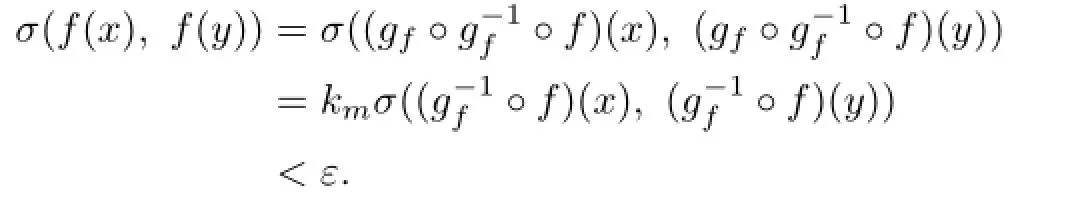
Therefore,the family is equicontinuous inΔ.This completes the proof of Theorem 1.10.
Proof of Theorem 1.11Let MWe can fi nd nonzero constants b and c satisfying M=For each f∈F,de fi ne a M¨obius map gfby gf=and thus
such that
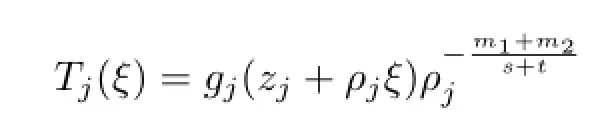
converges locally uniformly with respect to the spherical metric to a nonconstant meromorphic function T(ξ)whose spherical derivate is limited and T has order at most 2.By Lemmas 2.5 and 2.6,we get
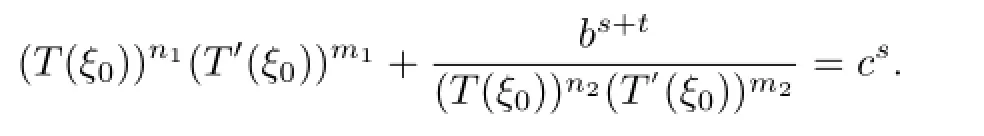
Finally,we get a contradiction by using Lemma 2.7,and in a similar way to the proof of Theorem 1.10,we can prove the Theorem 1.11 easily.This completes the proof of the theorem.
AcknowledgmentThis work was supported by the visiting scholar program of Chern institute of mathematics at Nankai University.The fourth author would like to express his hearty thanks to Chern institute of mathematics for providing very comfortable research environments to him as a visiting scholar.The authors thank the referees for reading the manuscript very carefully and making a number of valuable suggestions to improve the readability of the paper.
[1]Hayman W H.Meromorphic Functions.Oxford:Clarendon Press,1964.
[2]Bergweiler W.Bloch’s principle.Comput.Methods Funct.Theory,2006,6:77–108.
[3]Rubel L A.Four counterexamples to Bloch’s principle.Proc.Amer.Math.Soc.,1986,98: 257–260.
[4]Yang L.Value Distribution Theory.Berlin:Springer,1993.
[5]Schwick W.Normality criteria for families of meromorphic function.J.Anal.Math.,1989,52: 241–289.
[6]Beardon A F.Iteration of Rational Functions.New York:Springer-Verlag,1991.
[7]Pang X C,Zalcman L.Normality and shared values.Ark.Mat.,2000,38:171–182.
[8]Singh A P,Singh A.Sharing values and normality of meromorphic fuctions.Complex Variables Theory Appl.,2004,49(6):417–425.
[9]Hayman W K.Research Problems in Function Theory.London:The Athlone Press of Univ. London,1967.
[10]Lahiri I.A simple normality criterion leading to a counterexample to the converse of the Bloch principle.New Zealand J.Math.,2005,34:61–65.
[11]Yuan W J,Wei J J,Lin J M.A note on normal families of meromorphic functions concerning shared values.Discrete Dyn.Nat.Soc.,2011,article ID 463287:1–10.
[12]Charak K S,Rieppo J.Two normality criteria and the converse of the Bloch principle.J. Math.Anal.Appl.,2009,353:43–48.
[13]Zalcman L.Normal families:New perspectives.Bull.Amer.Math.Soc.,1998,35:215–230.
[14]Chen H H,Fang M L.On the value distribution of fnf′.Sci.China Ser.A,1995,38:789–798. [15]Yang C C,Hu P C.On the value distribution of ff(k).Kodai Math.J.,1996,19:157–167.
tion:30D30,30D45
A
1674-5647(2014)01-0081-09
Received date:Dec.11,2012.
Foundation item:The NSF(11271090)of China,the NSF(S2012010010121)of Guangdong Province,and the Graduate Research and Innovation Projects(XJGRI2013131)of Xinjiang Province.
*Corresponding author.
E-mail address:chenwei198841@126.com(Chen W),tianhg@xjnu.edu.cn(Tian H G).
杂志排行
Communications in Mathematical Research的其它文章
- Cocycle Perturbation on Banach Algebras
- Open Loop Saddle Point on Linear Quadratic Stochastic Di ff erential Games
- Stochastic Nonlinear Beam Equations with L´evy Jump
- Co fi niteness of Local Cohomology Modules with Respect to a Pair of Ideals
- Complete Convergence of Weighted Sums for Arrays of Rowwise m-negatively Associated Random Variables
- T∗-extension of Lie Supertriple Systems
