Open Loop Saddle Point on Linear Quadratic Stochastic Di ff erential Games
2014-03-03
(1.School of Basic Science,Changchun University of Technology,130012)
(2.College of Mathematics,Jilin University,Changchun,130012)
Open Loop Saddle Point on Linear Quadratic Stochastic Di ff erential Games
WANG JUN1,2
(1.School of Basic Science,Changchun University of Technology,130012)
(2.College of Mathematics,Jilin University,Changchun,130012)
Communicated by Li Yong
In this paper,we deal with one kind of two-player zero-sum linear quadratic stochastic di ff erential game problem.We give the existence of an open loop saddle point if and only if the lower and upper values exist.
stochastic di ff erential game,saddle point,open loop strategy
1 Introduction
In this paper,we consider the two-player zero-sum linear quadratic stochastic di ff erential games on a fi nite horizon.The fundamental theory of di ff erential games was given in 1965 by [1].Pontryagin’s Maximum Principle(see[2])and Bellman’s Dynamic Programming(see [3])are applied to games.Bensoussan[4],Bensoussan and Friedman[5]studied stochastic di ff erential games.It is well known that the existence of open loop saddle points guarantees the existence of the value of the di ff erential games;the existence and equivalence of the lower and upper values guarantee the existence of the value of the di ff erential games.These statements can be found,for instance,in[6–8].
Zhang[9]considered the two-person linear quadratic di ff erential games and showed that the value of the game exists if and only if both the upper and lower values exist.The same outcomes were proved by Delfour[10]by using another way.Specially,Mou and Yong[11]discussed two-person zero-sum linear quadratic stochastic di ff erential games in Hilbert spaces. The stochastic form of this problem is studied in this paper and we can achieve the same outcomes:No need of equivalence of the lower and upper values,we can prove the existence of the saddle point if and only if the lower and upper values exist.Due to stochastic op-timal control(see[4],[12])is concerned,in the present paper we use the Peng’s stochastic maximum principle(see[12])to gain the adjoint equation of this stochastic state system.
This paper is organized as follows:Section 2 provides the basic framework.Some results of payo fffunction are discussed in Section 3.The main outcomes are characterized in Section 4,where we prove the existence of the saddle point by the existence of lower and upper values in this di ff erential game.
2 Statement of the Problem
LetΩbe a bounded smooth domain in Rn,(Ω,F,P)be a probability space with fi ltration Ft,and W(·)be an Rn-valued standard Wiener process.We assume that
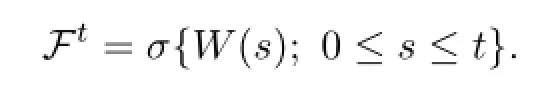
Let x be a solution of the following stochastic di ff erential equation:
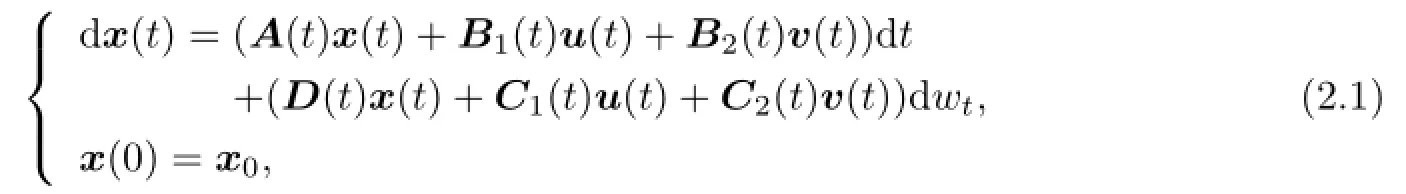
where x0is the initial state at time t=0.We call that u(t)∈L2(0,T;Rm),m≥1,is the strategy of the fi rst player if,u(·)is an Ft-adapted process with values in U(a nonempty subset of Rm(control domain))such that
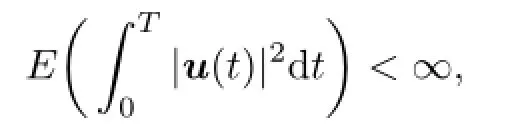
and v(t)∈L2(0,T;Rk),k≥1,is the strategy of the second player.
For any choice of controls u,v,we have the following payo fffunction:
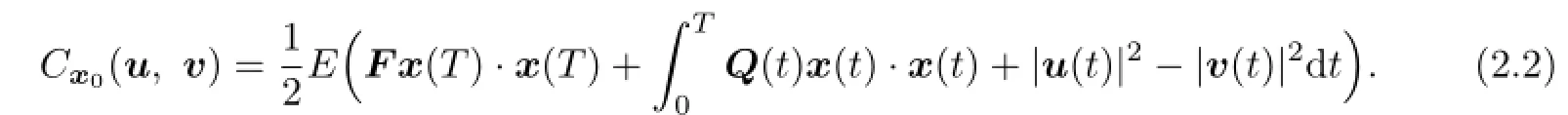
We assume that F is an n×n matrix,and A(t),B1(t),B2(t),C1(t),C2(t),D(t)and Q(t) are matrix functions of appropriate order that are measurable and bounded a.e.in[0,T]. Moreover,F and Q(t)are symmetrical.We write A,B1,B2,C1,C2,D and Q instead of A(t),B1(t),B2(t),C1(t),C2(t),D(t)and Q(t)throughout this paper and use the above assumptions.T>0 is a given fi nal time.|x|and x·y are the usual norm and inner product, respectively.
The more general quadratic structure involving cross terms and di ff erent quadratic weights N1u·u and N2v·v on u and v can be simpli fi ed to our model(see[10]).
De fi nition 2.1The game is said to achieve its open loop lower value if

is fi nite and is said to achieve its open loop upper value if
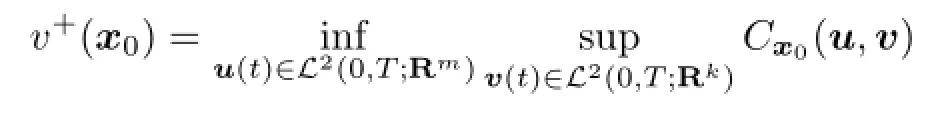
is fi nite.
Obviously,we always have

De fi nition 2.2If bothv−(x0)andv+(x0)exist andv−(x0)=v+(x0),then we say that the open loop value of the game exists and is denoted byv(x0).
De fi nition 2.3A pair of controls(¯u,¯v)∈L2(0,T;Rm)×L2(0,T;Rk)is called an open loop saddle point of the stochastic di ff erential game(2.1)with payo ff(2.2),if for all(t,x)∈(0,T)×Ω,u∈L2(0,T;Rm)andv∈L2(0,T;Rk),
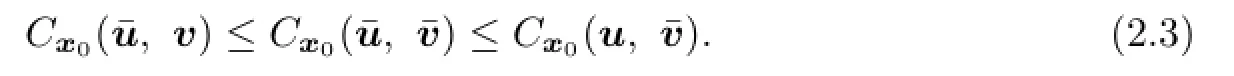
By De fi nition 2.3,(2.3)is equivalent to
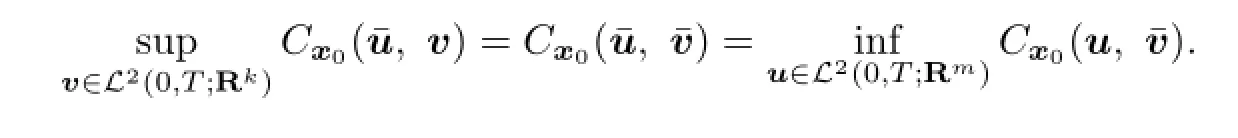
De fi nition 2.4Forx0∈Rn,we de fi ne
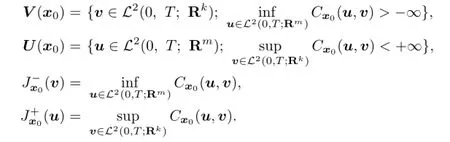
3 Some Results of Payo ffFunction
Since the payo fffunction(2.2)is quadratic,it is in fi nitely di ff erentiable.We can prove

where x is the solution of(2.1)and¯y is the solution of
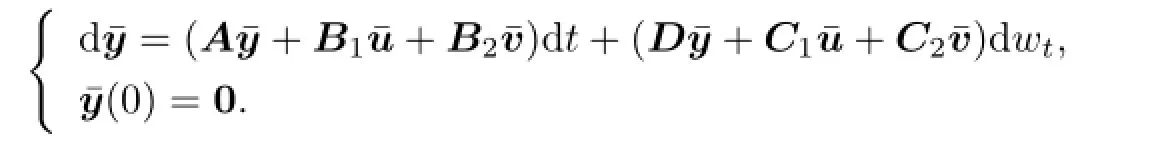
De fi nition 3.1Given a real functionfde fi ned on a Banach spaceB,the fi rst directional semiderivative atxin the directionv(when it exists)is de fi ned as
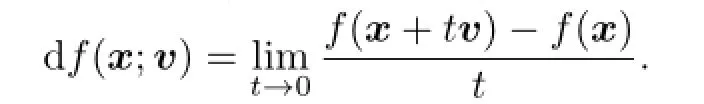
The second order bidirectional derivative atxin the directions(v,w)(when it exists)is de fi ned as
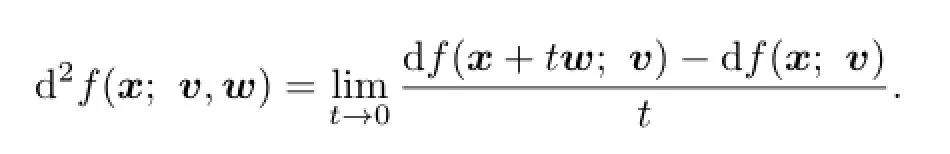

According to adjoint equation of(2.1)and(2.2),we can rewrite expression(3.1)in another form.Therefore,we quote some remarks on the stochastic di ff erential control.
According to the de fi nition of directional derivative,we have
We de fi ne the Hamiltonian by
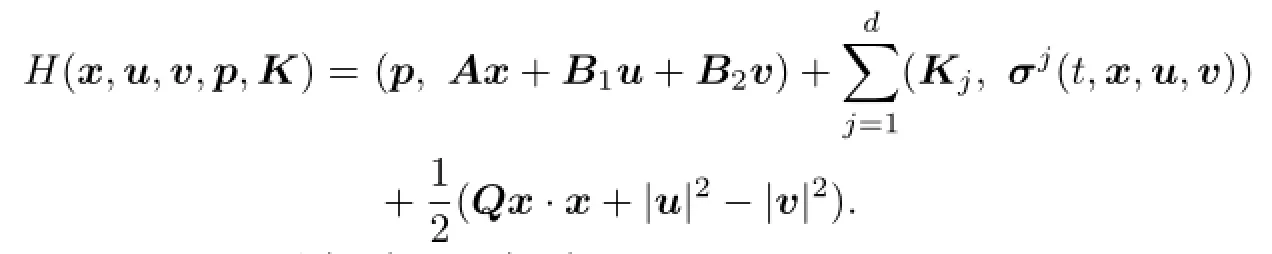
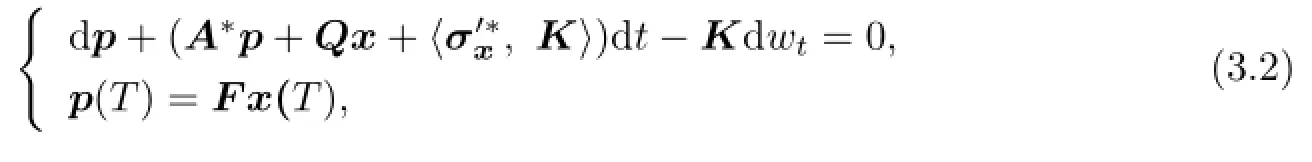
where
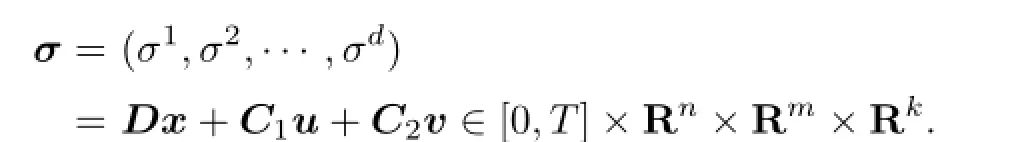
Moreover,(p(·),K(·))∈L2(0,T;Rn)×(L2(0,T;Rn))dand K=(K1,K2,···,Kd),
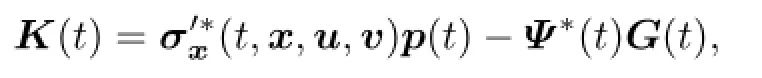
The adjoint equation of(2.1)and(2.2)is {
where Ψ(t)is de fi ned by
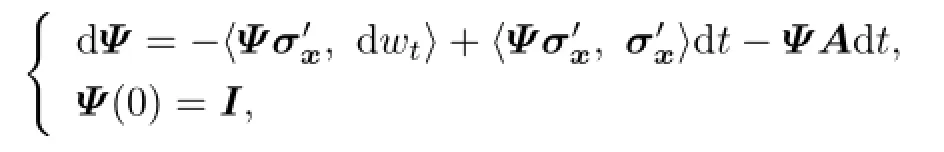
and
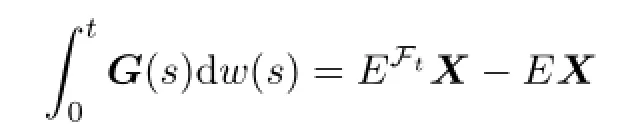
with
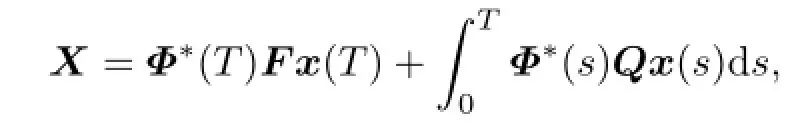
where Φ(t)is de fi ned by
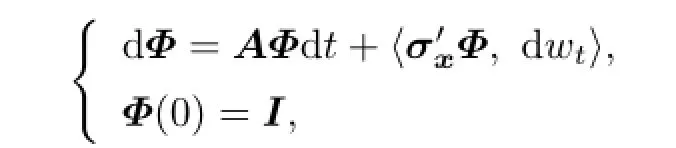
and the following property holds
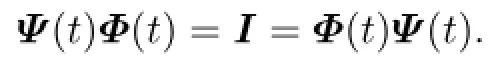
For the above assumptions and discussions about Hamiltonian and the adjoint equation, see[12]and[4].
Proposition 3.1According to adjoint equation(3.2),we can rewrite expression(3.1)in the following form:
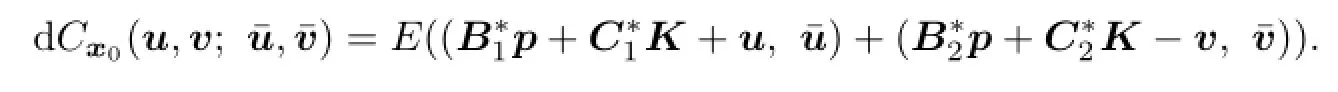
Proof.By Itˆo formula,

Thus
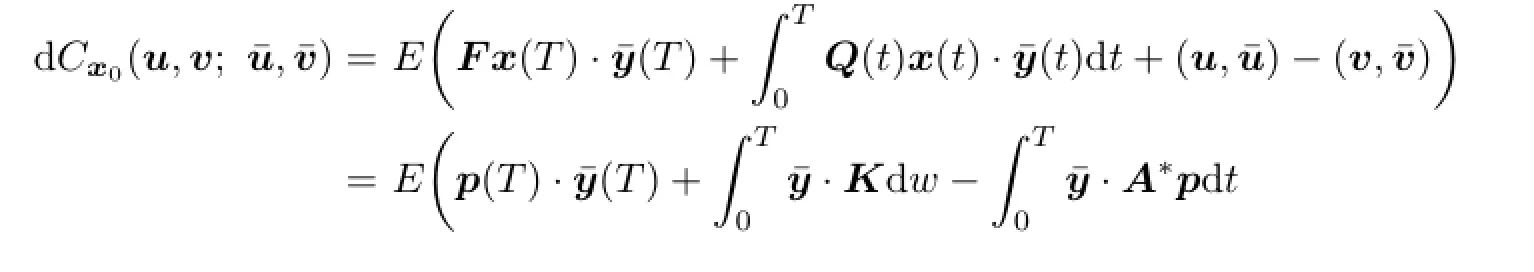
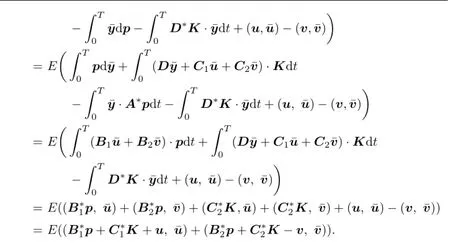
Similarly,the second order bidirectional derivative of payo fffunction is of the following form:
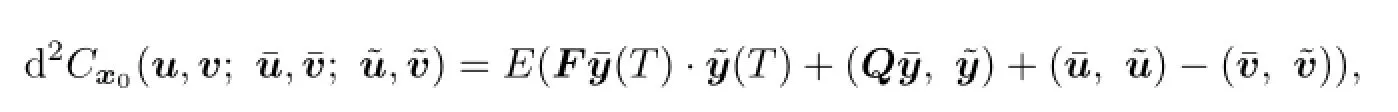
where
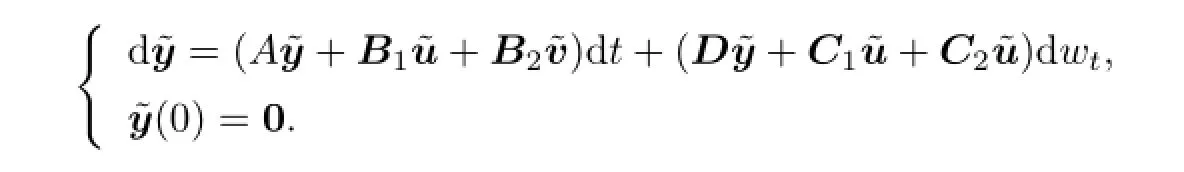
In particular,for all x0,u,v,and

Namely,the second order bidirectional derivative of payo fffunction is independent of x0and(u,v).So we have the following lemma.
Lemma 3.1The following statements are equivalent:
(1)The mapu→C0(u,0):L2(0,T;Rm)→Ris convex;
(2)For allu∈L2(0,T;Rm),C0(u,0)≥0;
(4)For allvandx0,the mapu→Cx0(u,v):L2(0,T;Rm)→Ris convex.
Corollary 3.1The following statements are equivalent:
(1)The mapv→C0(0,v):L2(0,T;Rk)→Ris concave;
(2)For allv∈L2(0,T;Rk),C0(0,v)≤0;
(4)For alluandx0,the mapv→Cx0(u,v):L2(0,T;Rk)→Ris concave.
Corollary 3.2The following statements are equivalent:
(1)The map(u,v)→C0(u,v):L2(0,T;Rm)×L2(0,T;Rk)→Ris(u,v)-convexconcave.That is,for anyv∈L2(0,T;Rk),
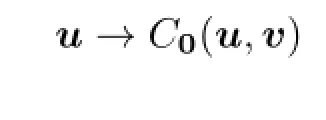
is convex,and for anyu∈L2(0,T;Rm),
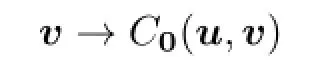
is concave;
(2)The pair(0,0)is a saddle point ofC0(u,v):

(3)For allx0,the map(u,v)→Cx0(u,v):L2(0,T;Rm)×L2(0,T;Rk)→Ris(u,v)-convex-concave.That is,for anyv∈L2(0,T;Rm),
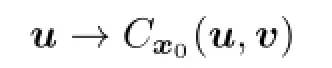
is convex,and for anyu∈L2(0,T;Rm),

is concave.
Theorem 3.1IfV(x0)̸=∅andU(x0)̸=∅,then the saddle point of payo ffC0(u,v)exists and it is(0,0).
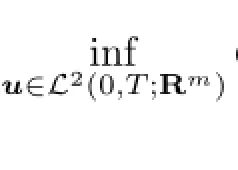
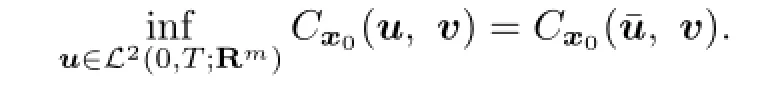
Thus
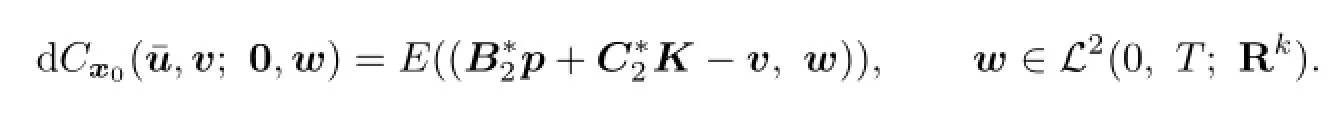
From the de fi nition of directional derivative one has
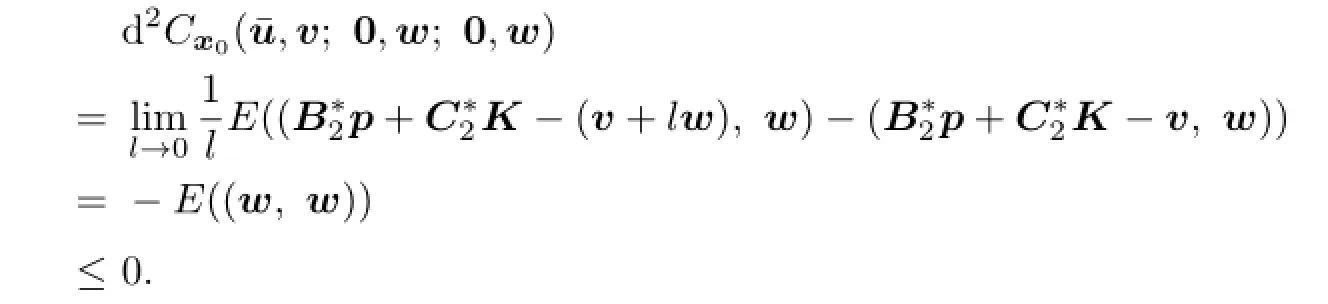
By(3.3),it follows that
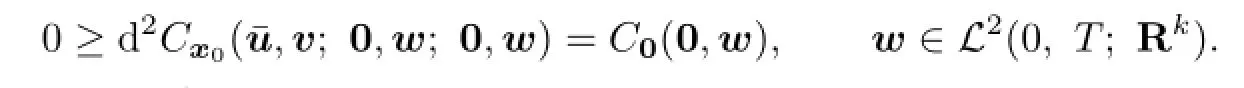
By Corollary 3.1 we have

So
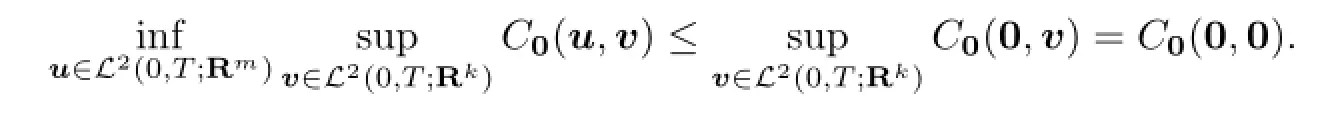
Similarly,since U(x0)̸=∅,by Lemma 3.1,we have

Hence
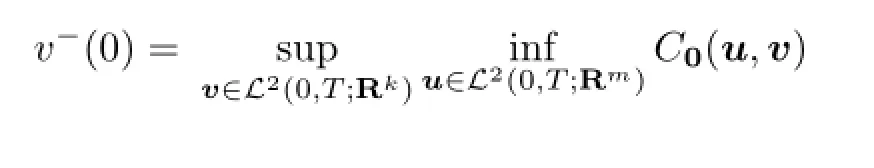
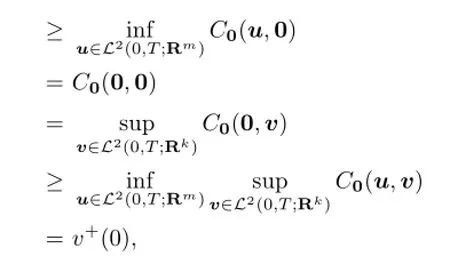
which shows that the saddle point of the payo ffC0(u,v)exists and it is(0,0).The proof is completed.
Now we show the payo ffCx0of the game when
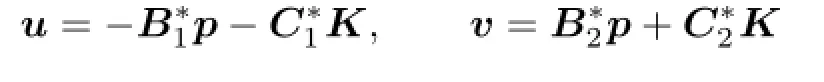
in(2.1).
Theorem 3.2There exists a solution(x,p,K)of the adjoint system

If
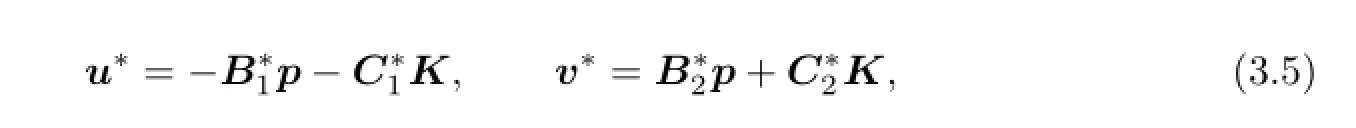
then
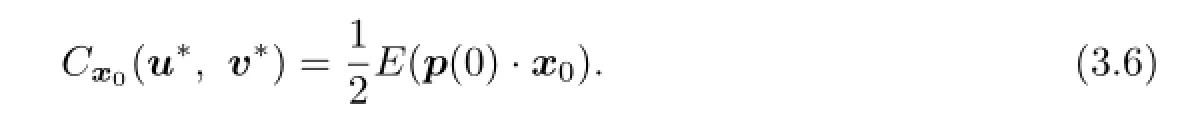
Proof.Byformula one has
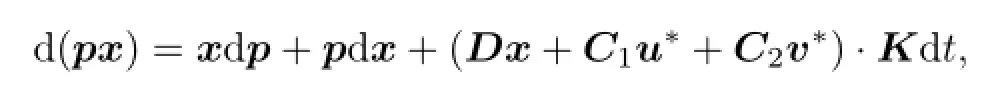
and

Then
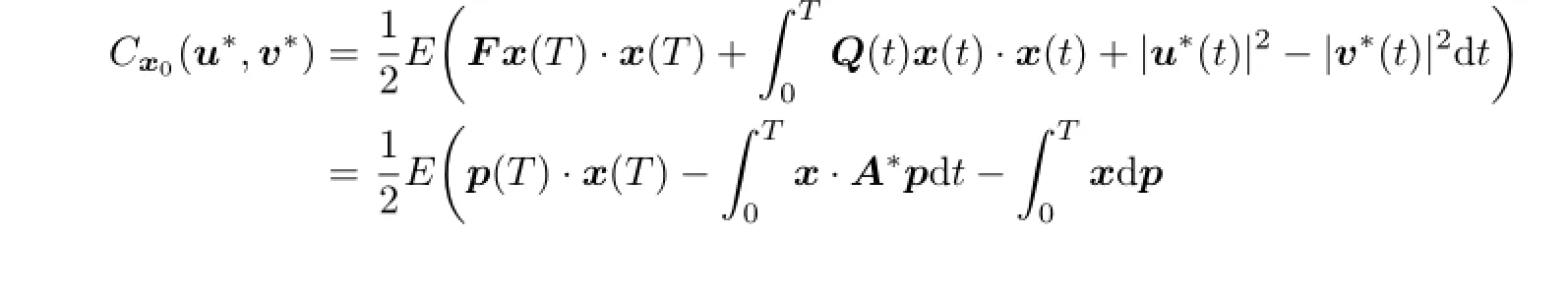
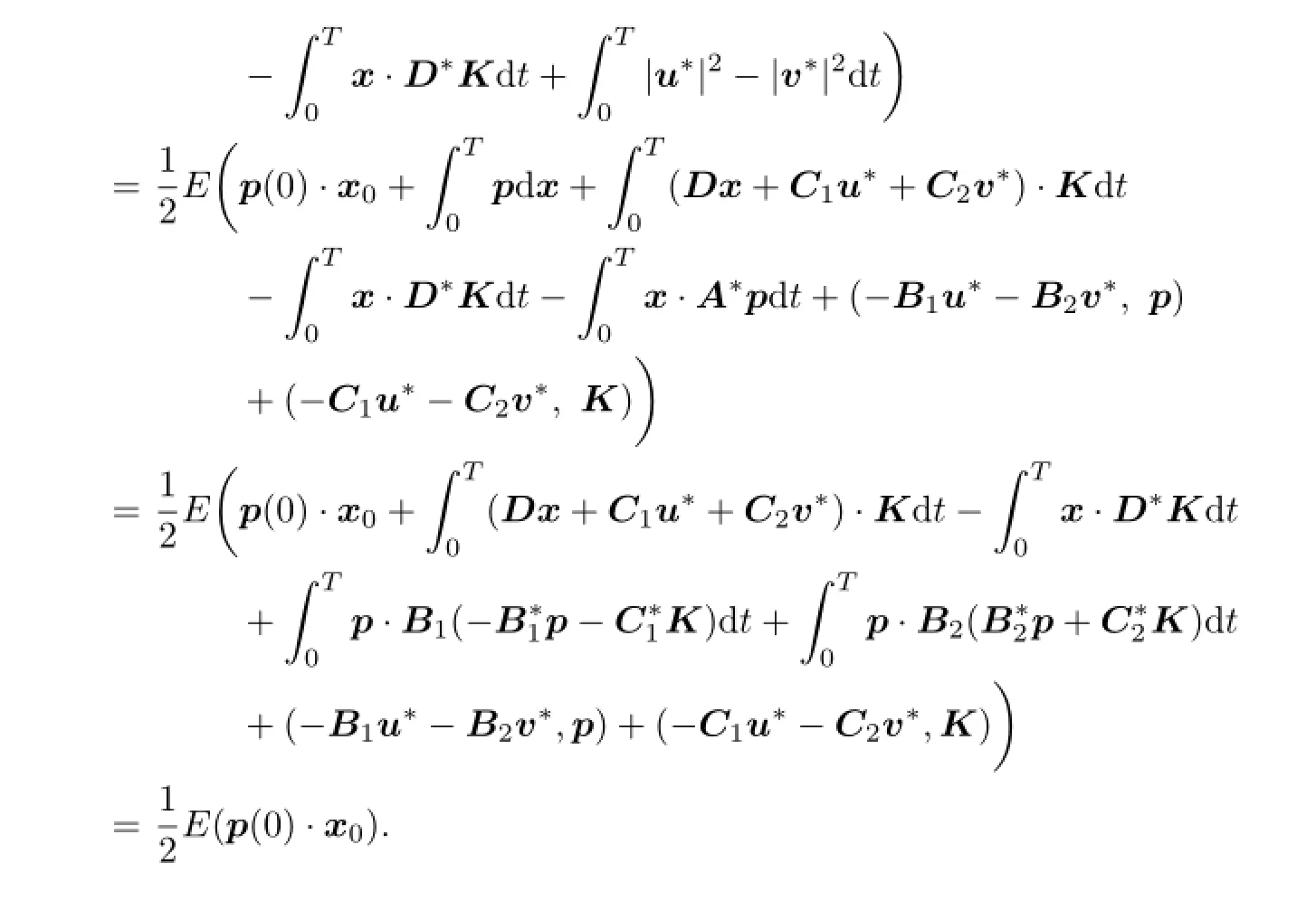
4 Main Results
In this section,we prove the existence of the saddle point of the system(2.1)-(2.3)if and only if the lower and upper values exist.
De fi nition 4.1We de fi ne
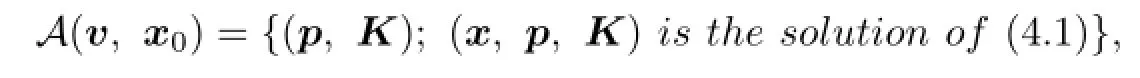
and
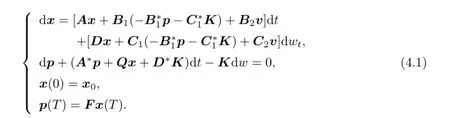
The main result in this paper is the following theorem.
Theorem 4.1Consider the stochastic di ff erential game(2.1)and(2.3).The following statements are equivalent:
(1)There exists an open loop saddle point ofCx0(u,v);
(2)The value of the game exists;
(3)Both the lower value and the upper value of the game exist.
The proof of Theorem 4.1 is discussed later.To prove it,some other theorems and discussions are needed.Firstly,we consider a part of Theorem 4.1:the open loop lower value of the game.
Theorem 4.2The following statements are equivalent:
(1)There existu∗∈L2(0,T;Rm)andv∗∈L2(0,T;Rk)such that
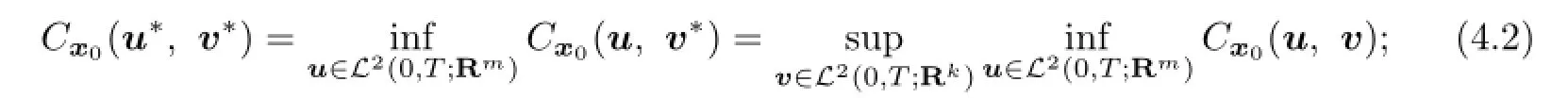
(2)The open loop lower valuev−(x0)of the game exists;
(3)There exists a solution(x,p,K)of the adjoint system(3.4)such thatV(x0),the solution pairs(u∗,v∗)is(3.5),and the open loop lower value are given by(3.6).
Proof.To prove this theorem,we need four steps.
(a)We show that if lower value exists,then for any v∈V(x0),one has

where(p,K)∈A(v,x0).
By the standard stochastic extremal principle(see[4]),(2.1)and(3.2),u∗is an optimizer if

Similarly to Theorem 3.2,we can get(4.3).
(b)We show that if lower value exists,then the following statements hold:
(i)
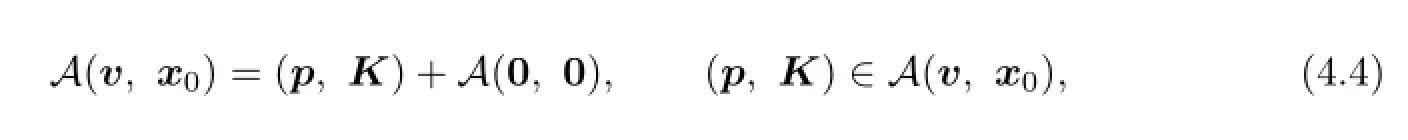
where
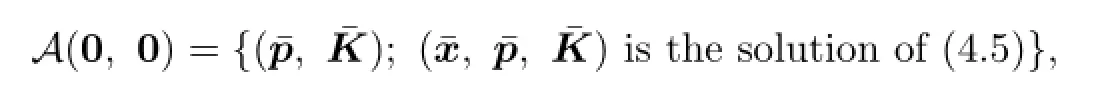
and
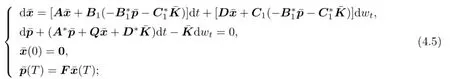
(ii)For all v∈V(0),
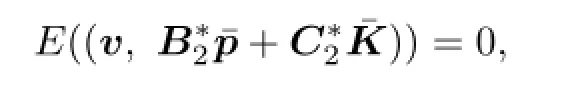
and we denote V(0)=B⊥in the sense of expectation;
(iii)
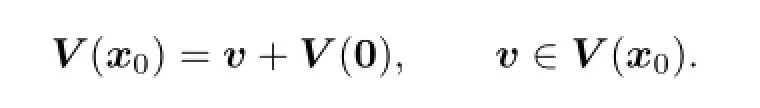
The di ff erential game(2.1)can be written as
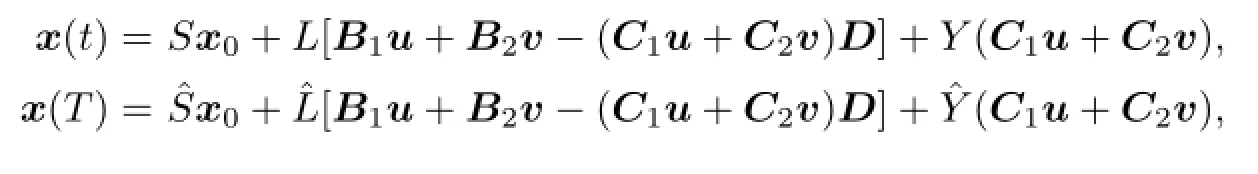
where
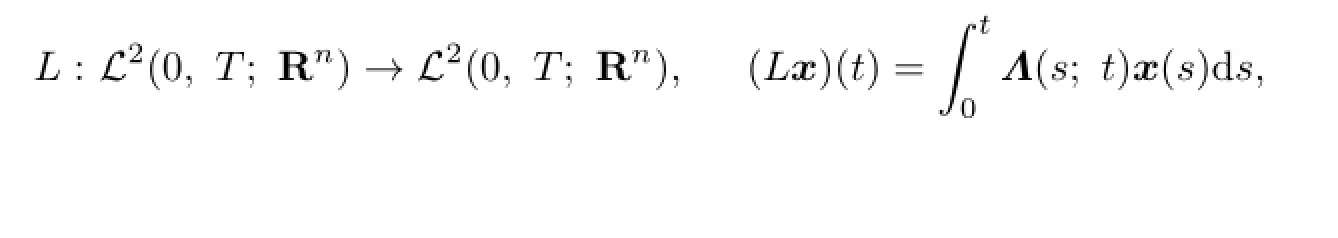
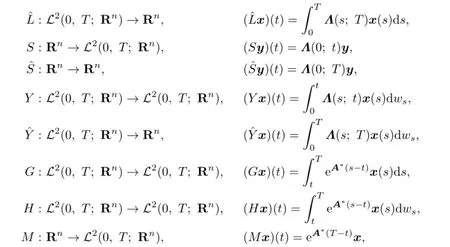
and
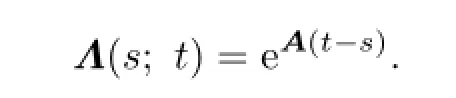
We denote by R∗the adjoint operator of the operator R.Let
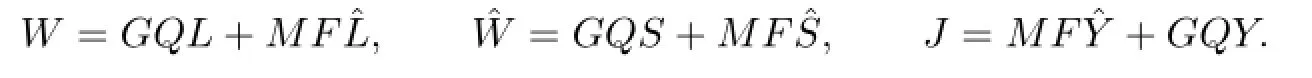
Then(4.1)can be written as
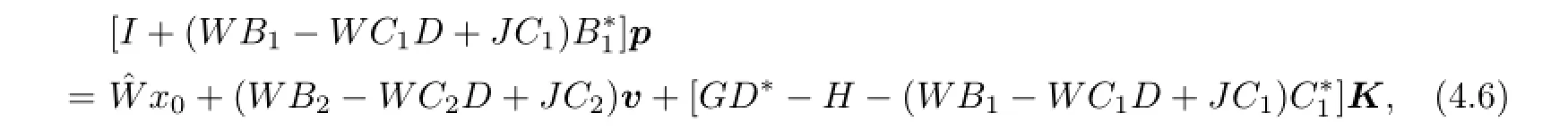
and(4.5)can be written as

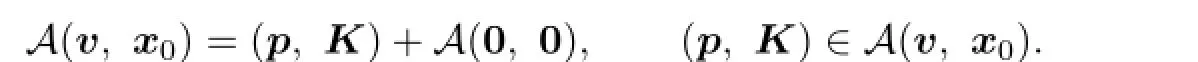
Given v∈V(x0),for all(p,K)∈A(v,x0)and∈A(0,0),we have
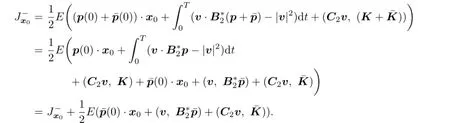
So
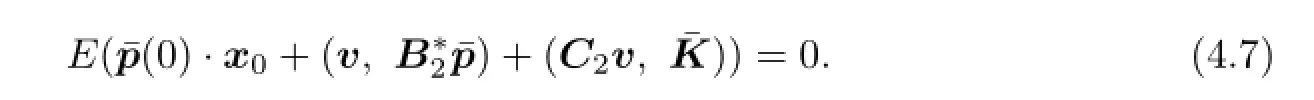
For all v∈V(0),we have
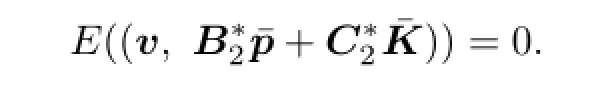
Let
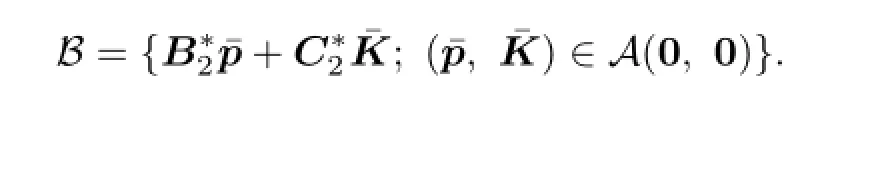
We say that V(0)=B⊥in the sense of expectation.It is easy to prove that

(c)We show that if the lower value exists,then there exist v∈V(x0)and(p∗,K∗)∈A(v,x0)such that

where(x∗,p∗,K∗)is the solution of(4.1).
Since the lower value of the game exists,there exists a v0∈V(x0)such that for any w∈V(0),
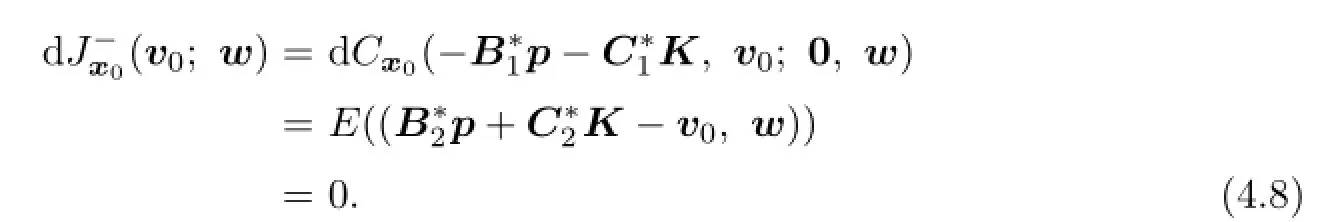
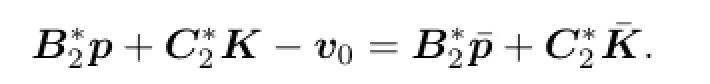
By(4.4),there exists(p∗,K∗)∈A(v0,x0)such thatand(x∗,p∗,K∗) is the solution of(4.1).Therefore,(x∗,p∗,K∗)is the solution of(3.4).By Theorem 3.2, the open loop lower value is given by(3.6).
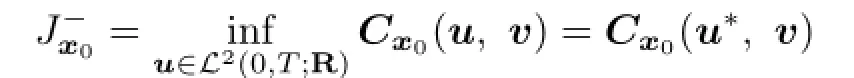
can achieve maximization at v∗.
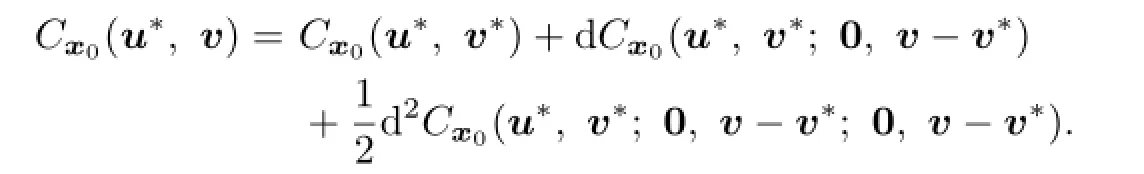
By(4.8)and v−v∗∈V(0)we have
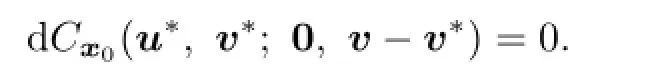
According to the de fi nition of directional derivative,we have
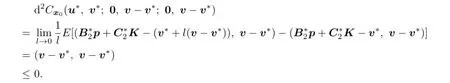
Thus
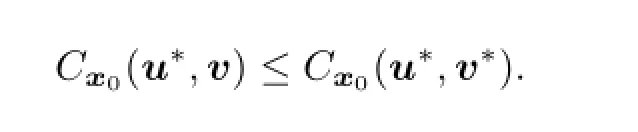
Now we go back to the proof of Theorem 4.2.
It is obvious that(1)⇒(2).
According to the above(a)–(c),we have(2)⇒(3).
(3)⇒(1).By(d),

So
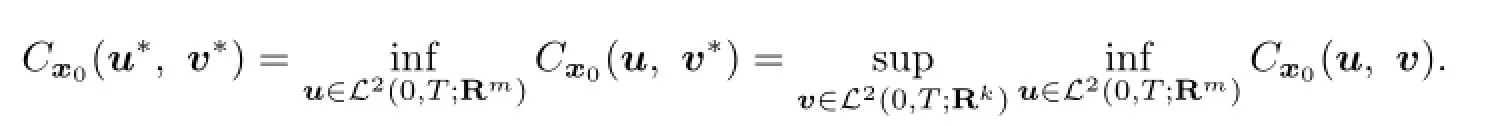
The proof is completed.
Corresponding to the Theorem 4.2,we have
Theorem 4.3The following statements are equivalent:
(1)There existu∗∈L2(0,T;Rm)andv∗∈L2(0,T;Rk)such that
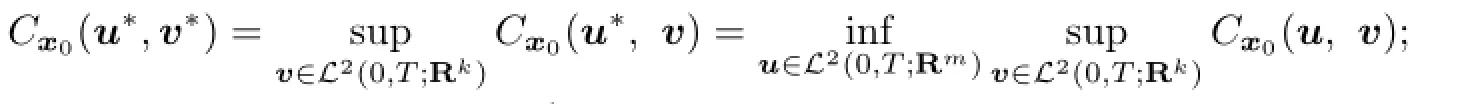
(2)The open loop upper valuev+(x0)of the game exists;
(3)There exists a solution(x,p,K)of the adjoint system(3.4)such thatthe solution pairs(u∗,v∗)is(3.5),and the open loop lower value is given by(3.6).
Now we give the proof of Theorem 4.1.
Proof of Theorem 4.1(1)⇒(2)⇒(3)are obvious.
(3)⇒(1).By Theorems 4.2 and 4.3,there exists a solution(x,p,K)of the system (3.10).Therefore,the game has a saddle point.
[1]Isaacs R.Di ff erential Games.New York:John Wiley and Sons,1965.
[2]Pontryagin L S,Boltyanskii V G,Gamkrekidze R V,Mishchenko E F.The Mathematical Theory of Optimal Processes.New York:Interscience Publishers,1962.
[3]Bellman R.Dynamic Programming.Princeton:Princeton Univ.Press,1957.
[4]Bensoussan A.Nonlinear Filtering and Stochastic Control.Lecture Notes in Math.vol.972. Berlin-Heidelberg-New York:Springer,1982.
[5]Bensoussan A,Friedman A.Nonzero-sum stochastic di ff erential games with stopping times and free boundary problems.Trans.Amer.Math.Soc.,1977,231(2),275–327.
[6]Ho Y C,Bryson A E,Baron Jr S.Di ff erential games and optimal pursuit-evasion strategies, IEEE Trans.Automat.Control,1965,AC-10:385–389.
[7]Case J H.Toward a theory of many player di ff erential games.SIAM J.Control Optim.,1969,7:179–197.
[8]Starr A W,Ho Y C.Nonzero-sum di ff erential games.J.Optim.Theory Appl.,1969,3:184–206.
[9]Zhang P.Some results on two-person zero-sum linear quadratic di ff erential games.SIAM J. Control Optim.,2005,43(6):2157–2165.
[10]Delfour M C.Linear quadratic di ff erential games:saddle point and riccati di ff erential equation. SIAM J.Control Optim.,2007,46(2):750–774.
[11]Mou L B,Yong J M.Two-person zero-sum linear quadratic stochastic di ff erential games by a Hilbert space method,J.Indian Manag.Optim.,2006,2:93–115.
[12]Peng S.A general stochastic maximum principle for optimal control problems.SIAM J.Control Optim.,1990,28(4):966–979.
tion:91A23
A
1674-5647(2014)01-0011-12
Received date:Jan.4,2011.
Foundation item:The Young Research Foundation(201201130)of Jilin Provincial Science&Technology Department,and Research Foundation(2011LG17)of Changchun University of Technology.
E-mail address:0435lover@163.com(Wang J).
杂志排行
Communications in Mathematical Research的其它文章
- Cocycle Perturbation on Banach Algebras
- Stochastic Nonlinear Beam Equations with L´evy Jump
- Co fi niteness of Local Cohomology Modules with Respect to a Pair of Ideals
- Complete Convergence of Weighted Sums for Arrays of Rowwise m-negatively Associated Random Variables
- T∗-extension of Lie Supertriple Systems
- Generalized Extended tanh-function Method for Traveling Wave Solutions of Nonlinear Physical Equations
