Cocycle Perturbation on Banach Algebras
2014-03-03
(1.Department of Mathematics,Tianjin Polytechnic University,Tianjin,300160)
(2.Basic Department,Tianjin Vocational Institute,Tianjin,300410)
Cocycle Perturbation on Banach Algebras
SHI LUO-YI1AND WU YU-JING2
(1.Department of Mathematics,Tianjin Polytechnic University,Tianjin,300160)
(2.Basic Department,Tianjin Vocational Institute,Tianjin,300410)
Communicated by Ji You-qing
Let α be a fl ow on a Banach algebra B,and ta continuous function fromRinto the group of invertible elements of B such that usαs(ut)=us+t,s,t∈R. Then βt=Adut◦αt,t∈Ris also a fl ow on B,where Adut(B)for any B∈β is said to be a cocycle perturbation of α.We show that if α,β are two fl ows on a nest algebra(or quasi-triangular algebra),then β is a cocycle perturbation of α.And the fl ows on a nest algebra(or quasi-triangular algebra)are all uniformly continuous.
cocycle perturbation,inner perturbation,nest algebra,quasi-triangular algebra
1 Introduction
In the quantum mechanics of particle systems with an in fi nite number of degrees of freedom, an important problem is to study the di ff erential equation
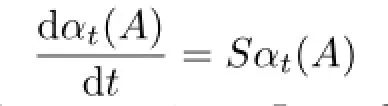
under variety of circumstances and assumptions.In each instance the A corresponds to an observable,or state,of the system and is represented by an element of some suitable Banach algebra B.S is an operator on B,and{αt}t∈Ris a group of bounded automorphisms on B.The function
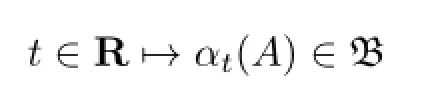
describes the motion of A.The dynamics are given by solutions of the di ff erential equation subject to certain supplementary conditions of continuity.Thus it is worth to study the group of bounded automorphisms on B.For more details see[1].
A fl ow α on B is a group homomorphism of the real line R into the group of bounded automorphisms on B(i.e.,tαt)such that
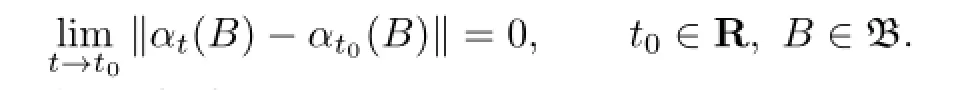
If there exists an h∈B such that
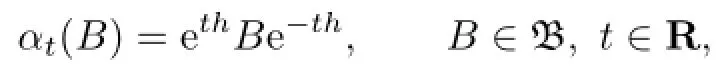
then we call α an inner fl ow.We say that a fl ow α is uniformly continuous if
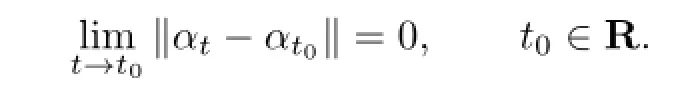
If α is a fl ow on B and if u is a continuous map of R into the group of invertible elements G(B)of B such that
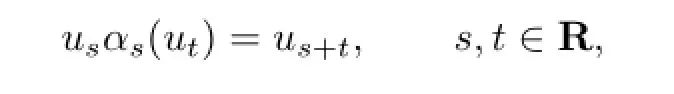
then we call u=(ut)t∈Ran α-cocycle for(B,R,α).Let
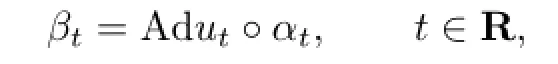
where
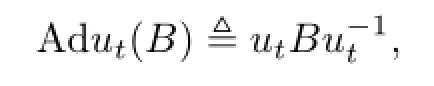
i.e.,
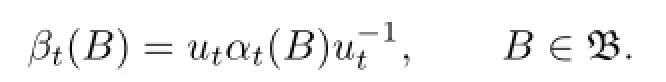
Then β is also a fl ow on B,and is said to be a cocycle perturbation of α.
If α is a fl ow on B,let D(δα)be composed of those B∈B for which there exists an A∈B with the property that
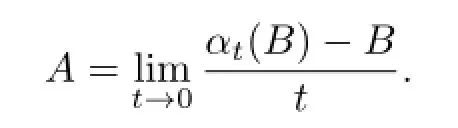
Then δαis a linear operator on D(δα)de fi ned by
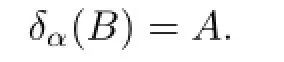
We call δαthe in fi nitesimal generator of α.By Proposition 3.1.6 of[1],δαis a closed derivation,i.e.,the domain D(δα)is a dense subalgebra of B and δαis closed as a linear operator on D(δα)and satis fi es
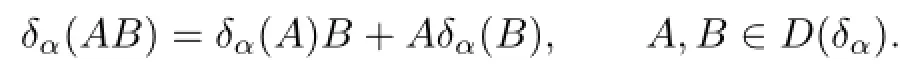
We call β an inner perturbation of α if α,β are two fl ows on B,
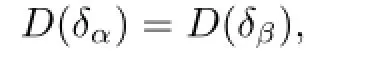
and there exists an h∈B such that
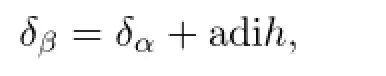
where i is the imaginary unit,and
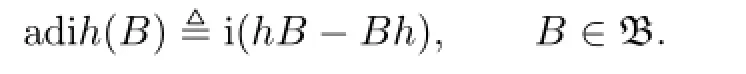
Moreover,
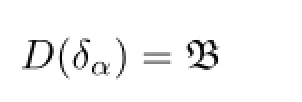
if and only if α is uniformly continuous.For more details see[1–2].

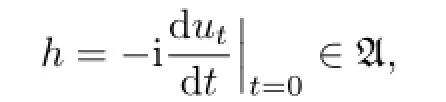
then the in fi nitesimal generator of the fl ow
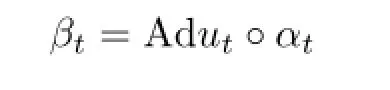
is given by
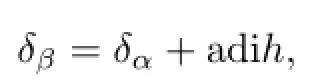
i.e.,β is an inner perturbation of α.Moreover,for any α-cocycle u=(ut)t∈R,there is a w∈G(A)and a di ff erentiable α-cocycle v=(vt)t∈R,i.e.,vtis an α-cocycle and di ff erentiable such that
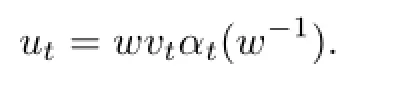
In Section 2,we consider the cocycle of fl ows on Banach algebras and obtain some similar results to[3].
It is well-known that a fl ow α on B may not be uniformly continuous even if B is a C∗-algebra(see[1–2]).In Section 3,we study the fl ows on a nest algebra τ(N)and the quasi-triangular algebra
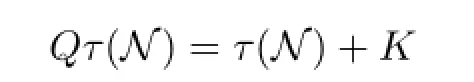
(see[11]).We recall that a nest N is a chain of closed subspaces of a Hilbert space H containing{0}and H which is,in addition,closed under taking arbitrary intersections and closed spans.The nest algebra T(N)associated with N is the set of all T∈B(H)which leave each element of the nest invariant.For instance,if H is separable with orthonormal basisand Hn=span{e1,···,en},then exists for any t0∈R,and
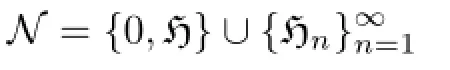
is a nest.In this case,T(N)is simply the set of all operators whose matrix representation with respect to this basis is upper triangular.It is obvious that τ(N)and Qτ(N)are typical Banach algebras.We obtain that all of the fl ows on τ(N)(or Qτ(N))are uniformly continuous.Moreover,all of the fl ows are cocycle perturbation to each other.
2 Cocycle Perturbations
Let B be a Banach algebra,α be a fl ow on B and u be an α-cocycle.Then

is a cocycle perturbation of α.In this section,we obtain that β is an inner perturbation of α if and only if u is di ff erentiable(see Theorem 2.1).Moreover,for any α-cocycle u,there is a di ff erentiable α-cocycle v and an inventible element w in B such that
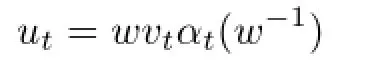
(see Theorem 2.2).
The following lemmas are useful for this paper.
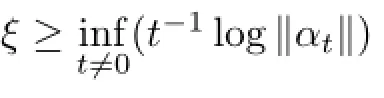
Lemma 2.2([1],Proposition 3.1.33)Letαbe a fl ow on a Banach algebraBwith in fi nitesimal generatorδα.For eachP∈Bde fi ne the bounded derivationδPby
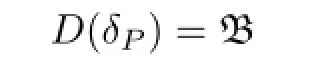
and
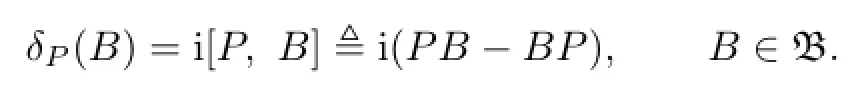
Thenδ+δPgenerates a fl ow onBgiven by
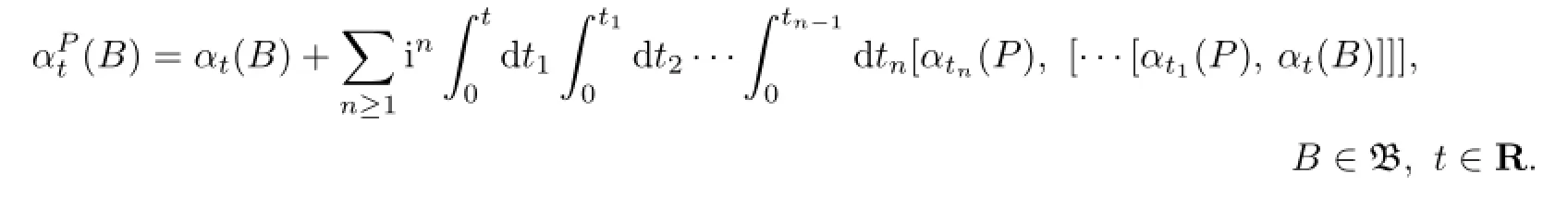
Lemma 2.3LetBbe a Banach algebra with unit1,αbe a fl ow onBandδdenote the in fi nitesimal generator ofα.Furthermore,for eachP∈B,de fi neδPas in Lemma2.2. Thenδ+δPgenerates a fl ow onBgiven by
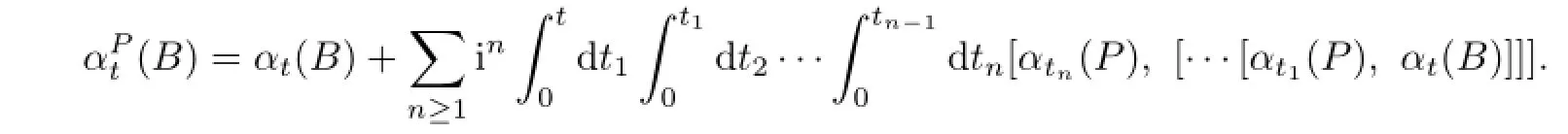
Moreover,
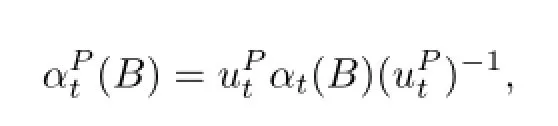
whereis a one-parameter family of invertible elements,determined by
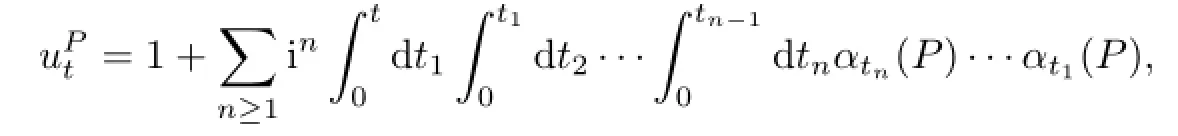
which satis fi es theα-cocycle relation

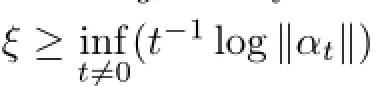
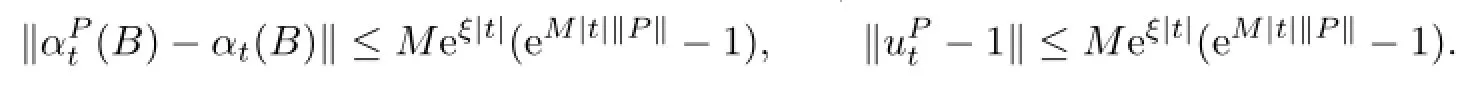
Proof.The fi rst statement of the lemma can be obtained from Lemma 2.2.We just give the proof of the last statement of this lemma.
We consider uPtde fi ned by the series.
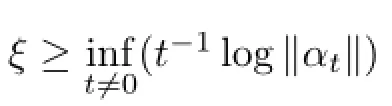
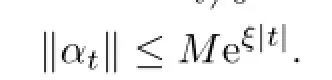
Let

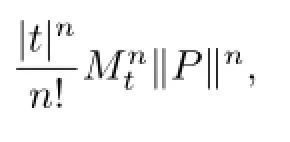
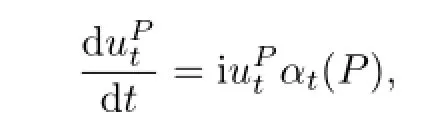
and
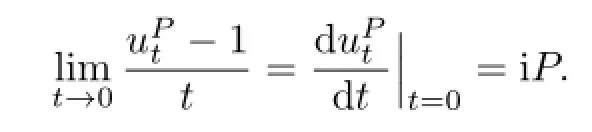
Hence,
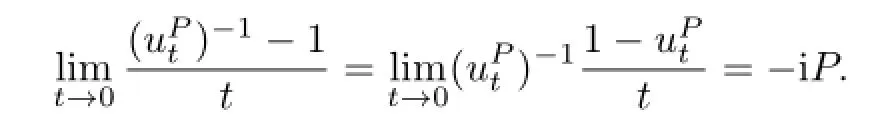
To establish the α-cocycle relation,we fi rst note that
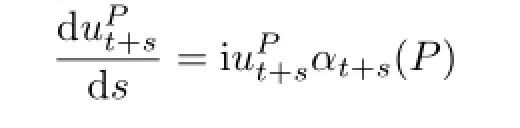
and
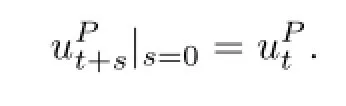
Since
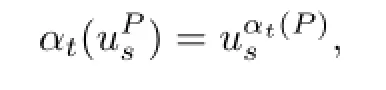
we can get
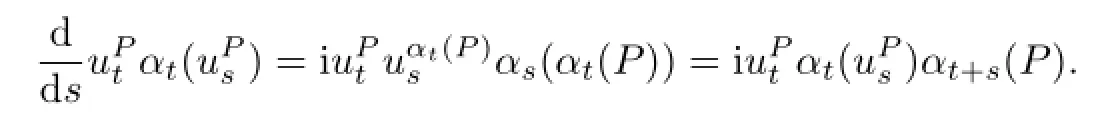
Moreover,
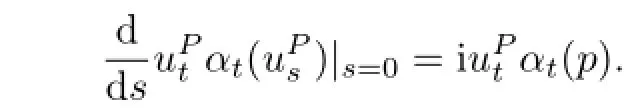
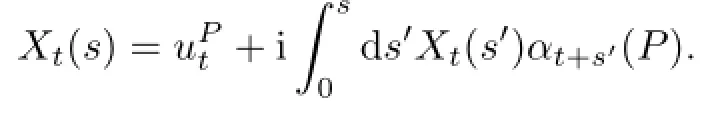
Hence,
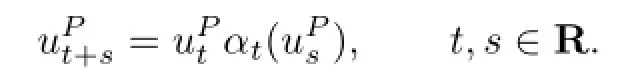
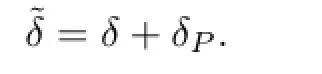
Choosing A∈D(δ+δP),one has
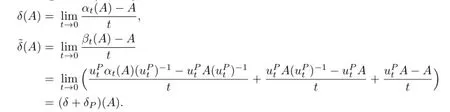
Similarly,if A∈D(˜δ),we obtain that
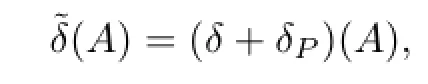
and then

Thus,by Theorem 3.1.26 in[1],one must have
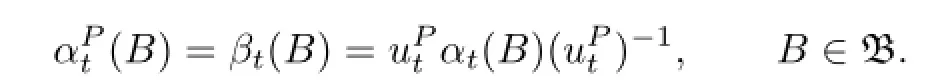
Theorem 2.1Letαbe a fl ow onB,(ut)t∈Rbe anα-cocycle,andβt=Adut◦αt.Thenβis an inner perturbation ofαif and only ifutis di ff erentiable.
Proof.Sufficiency.It follows immediately from Lemma 2.3.

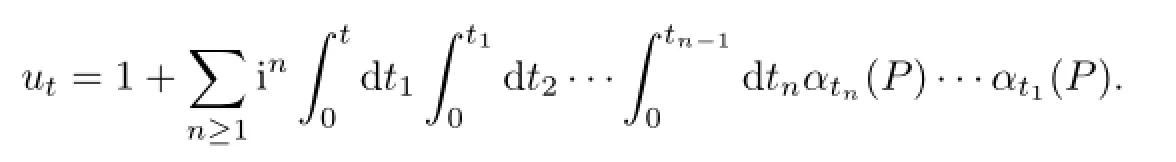
Hence,β is an inner perturbation of α by Lemma 2.3.
Corollary 2.1Adopt the assumptions of Lemma2.3and also assume thatαtis an inner fl ow,i.e.,there exists anh∈Bsuch that
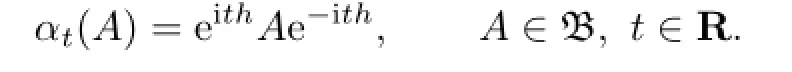
Then
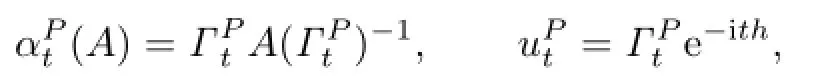
whereis de fi ned as in Lemma2.3,and
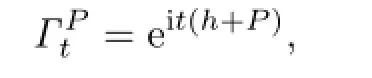
i.e.,is an inner fl ow.
Proof.If
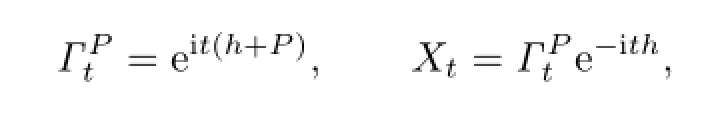
then

and X0=1.Thus,Xtis the unique solution of the integral equation
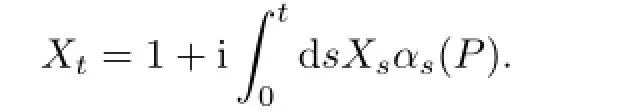
This solution can be obtained by iteration and one fi nds Xt=whereis de fi ned as in Lemma 2.3,and
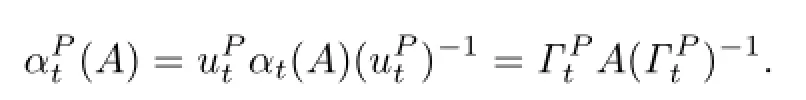
The proof is completed.
In the following we show that every α-cocycle is similar to a di ff erentiable α-cocycle.
De fi nition 2.1Letαbe a fl ow onB.A∈Bis called an analytic element forαif there exists an analytic functionf:C→Bsuch that
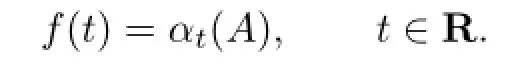
Lemma 2.4Letαbe a fl ow on the Banach algebraB,andM,ξbe constants such that
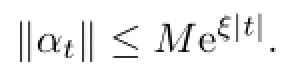
ForA∈B,de fi ne
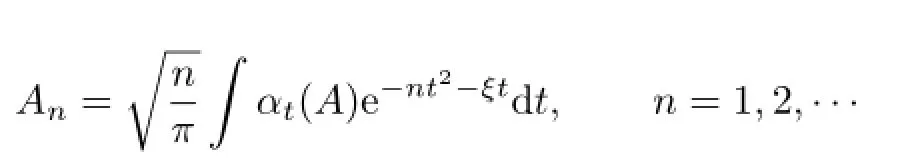
Then eachAnis an entire analytic element forαt,and there exists anNsuch that
‖An‖≤2M‖A‖, n≥N,andAn→Ain the weak topology asn→∞.In particular,theαanalytic elements form a normal-dense subspace ofB.
Proof.Since
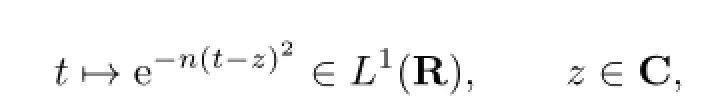
we know that
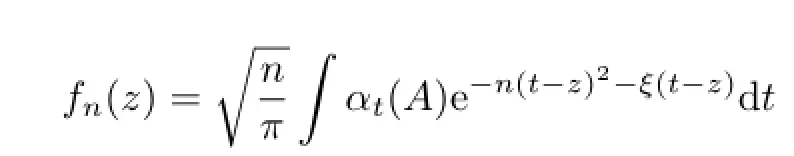
is well de fi ned for all z∈C.For z=s∈R,we have

But for η∈B∗we have
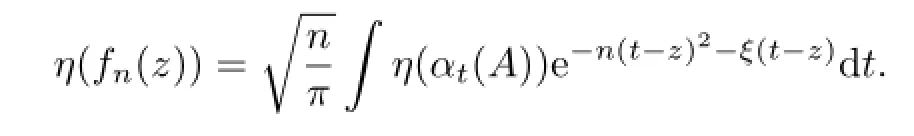
Since
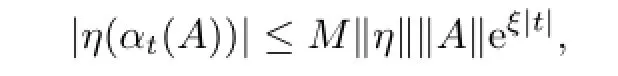
i
t follows from the Lebesgue dominated convergence theorem that tη(fn(z))is analytic.
Hence each Anis analytic for αt(A).Furthermore,we can derive the estimate
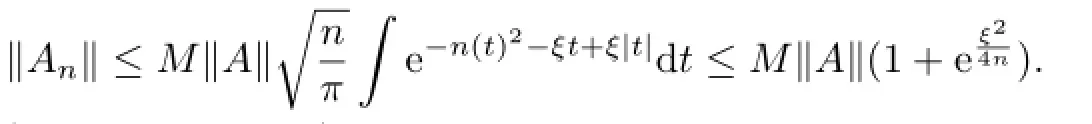
Hence,there exists an N such that

Noting that
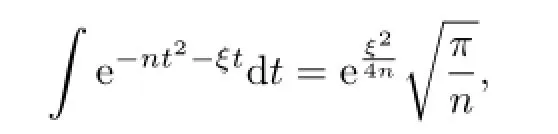
one has
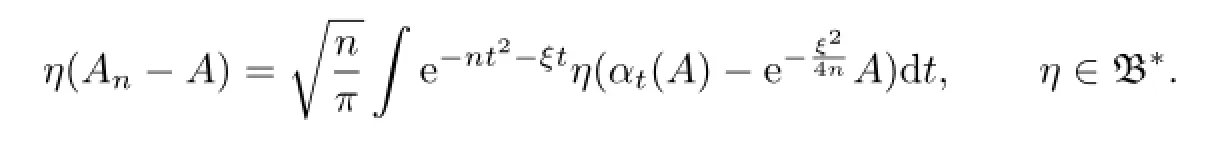
For any ε>0 we may choose a δ>0 such that|t|<δ implies
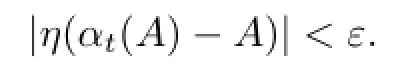
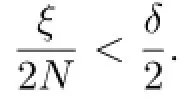
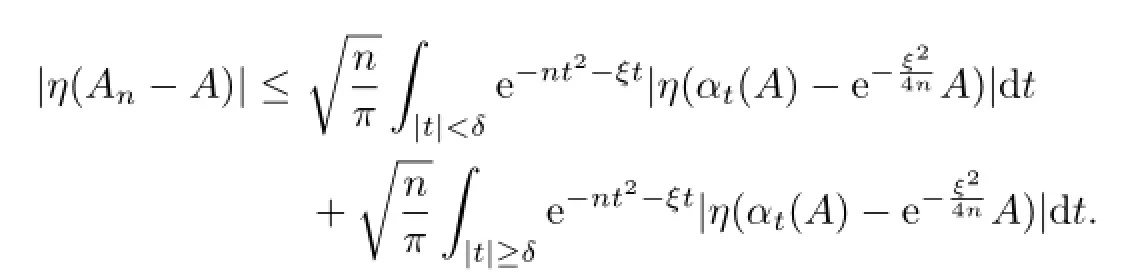
On the other hand,
√
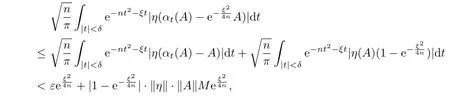
and
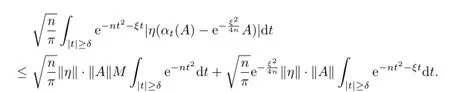
So,for any η∈B∗,
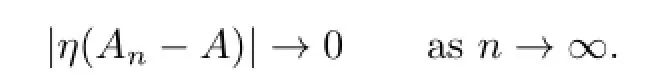
Finally,note that the norm closure and the weak closure of a convex set are the same,so the α analytic elements form a normal-dense subspace of B.
Theorem 2.2Ifuis anα-cocycle forB,then for a givenε>0there exist a di ff erentiableα-cocyclevand aw∈G(B)such that
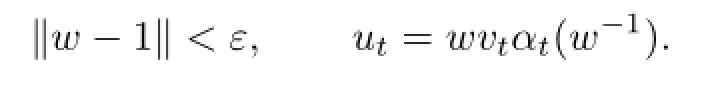
Proof.The proof is similar to that of Lemma 1.1 in[3]and is omitted.
For given two fl ows α and β on a unitary Banach algebra B,we say that β is a conjugate to α if there exists a bounded automorphism σ of B such that

Conjugate,cocycle perturbation and inner perturbation de fi ne three equivalence relations. We say that β is cocycle-conjugate to α if there exists a bounded automorphism σ of B such that β is a cocycle perturbation of σασ−1.This also de fi nes an equivalence relation among the fl ows.We say that α is approximately inner if there is a sequence{hn}in B such that
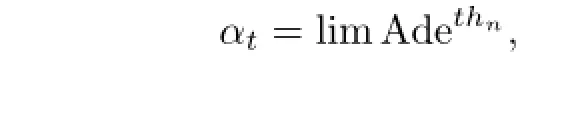
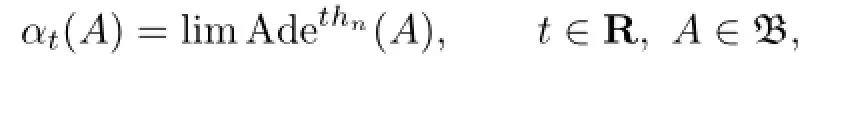
i.e.,or equivalently,uniformly continuous in t on every compact subset of R and every A∈B. A fl ow on a Banach algebra B is said to be asymptotically inner if there is a continuous function h of R+into B such that
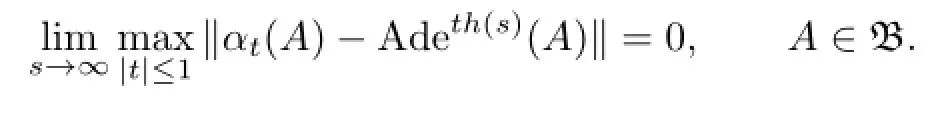
Corollary 2.2Letαandβbe two fl ows on Banach algebraB.Then the following conditions are equivalent:
(i)βis cocycle-conjugate toα;
(ii)βis an inner perturbation ofσασ−1for some automorphismσofB,whereσασ−1is the actiont
If one of above conditions is satis fi ed andαis inner(approximately or asymptotically inner), then so isβ.
Proof.The fi rst statement of the proposition can be obtained from Corollary 1.3 of[3].We just give the proof of the last statement of the corollary.
First we prove that if β is an inner perturbation of α,i.e.,
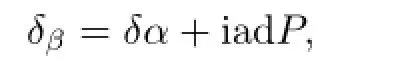
then it follows that if α is inner(approximately or asymptotically inner),so is β.
(a)If α is inner,then so is β by Corollary 2.1.
(b)If α is approximately inner,then there is a sequence{hn}in B such that
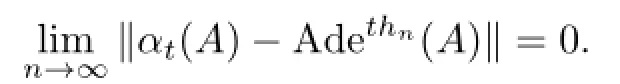
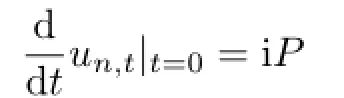
by means of Lemma 2.3.Since βt=Adut◦αtand un,t→ut,we obtain that

Besides,Adun,t◦αn,tis inner by Corollary 2.1.Then β is approximately inner.
(c)If α is asymptotically inner,then there is a continuous function h of R+into B such that
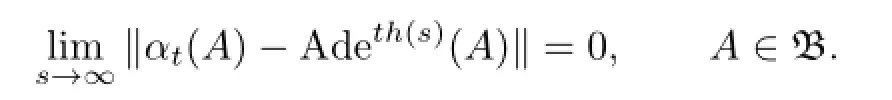
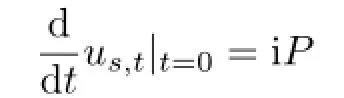
by means of Lemma 2.3.Since βt=Adut◦αtand us,t→ut,we obtain that

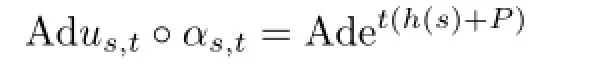
by Corollary 2.1.Then β is approximately inner.The proof is completed.
In the following we prove that if β is conjugate to α,i.e.,there is a bounded automorphism σ of B such that
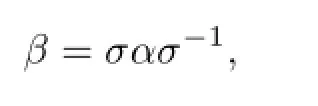
then,if α is inner(approximately or asymptotically inner),then so is β.
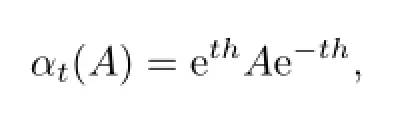
then

i.e.,β is inner.
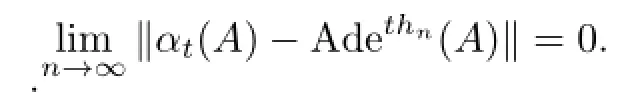
Because β is conjugate to α,i.e.,
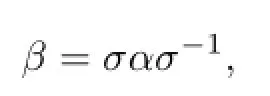
σ is the bounded automorphism of A,so there exists an M>0 such that
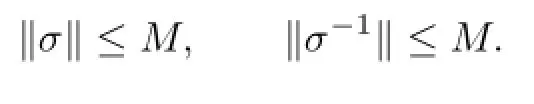
Therefore,
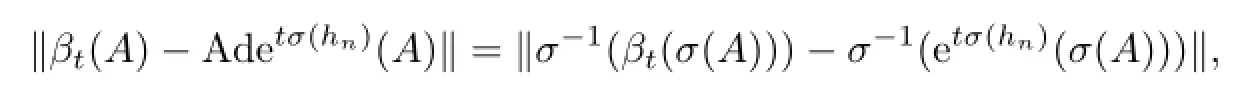
i.e.,β is asymptotically inner.
Finally,if β is cocycle-conjugate to α,then there is a bounded automorphism σ of B such that β is a cocycle perturbation of σασ−1.If α is inner(approximately or asymptotically inner),then so is σασ−1.Then so is β.
[1]Bratteli O,Robinson D W.Operator Algebras and Quantum Statistical Mechanics I.Berlin-Heidelberg-New York:Springer-Verlag,1979.
[2]Sakai S.Operator Algebras in Dynamical Systems.Cambridge:Cambridge Univ.Press,1991.
[3]Kishimoto A.Locally representable one-parameter automorphism groups of AF algebras and KMS states.Rep.Math.Phys.,2000,45:333–356.
[4]Kishimoto A.UHF fl ows and the fl ip automorphism.Rev.Math.Phys.,2001,13(9):1163–1181.
[5]Kishimoto A.Examples of one-parameter automorphism groups of UHF algebra.Comm.Math. Phys.,2001,216:395–428.
[6]Kishimoto A.Approximately inner fl ows on seperable C∗-algebras.Rev.Math.Phys.,2002,14:1065–1094.
[7]Kishimoto A.Approximate AF fl ows.J.Evolution Equation,2005,5:153–184.
[8]Kishimoto A.The one-cocycle property for shifts.Ergodic.Theory Dynam.Systems,2005,25: 823–859.
[9]Kishimoto A.Multiplier cocycles of a fl ow on a C∗-algebra.J.Funct.Anal.,2006,235:271–296.
[10]Kishimoto A.Lifting of an asymptotically inner fl ow for a separable C∗-algebra.in:Bratteli O, Neshveyev S,Skau C.The Abel Symposium 2004 Operator Algebras.Berlin:Springer,2006: 233–247.
[11]Davidson K R.Nest Algebras.Essex:Longman Group UK limited,1988.
tion:47D03,46H99,46K50,46L57
A
1674-5647(2014)01-0001-10
Received date:Sept.17,2010.
Foundation item:The NSF(11226125,10971079,11301379)of China.
E-mail address:shiluoyi@aliyun.com(Shi L Y).
杂志排行
Communications in Mathematical Research的其它文章
- Open Loop Saddle Point on Linear Quadratic Stochastic Di ff erential Games
- Stochastic Nonlinear Beam Equations with L´evy Jump
- Co fi niteness of Local Cohomology Modules with Respect to a Pair of Ideals
- Complete Convergence of Weighted Sums for Arrays of Rowwise m-negatively Associated Random Variables
- T∗-extension of Lie Supertriple Systems
- Generalized Extended tanh-function Method for Traveling Wave Solutions of Nonlinear Physical Equations
