Generalized Extended tanh-function Method for Traveling Wave Solutions of Nonlinear Physical Equations
2014-03-03
(1.Fundamental Department,Aviation University of Air Force,Changchun,130022)
(2.College of Mathematics and Statistics,Northeast Normal University, Changchun,130023)
(3.Key Laboratory of Symbolic Computation and Knowledge Engineering of Ministry of Education,Jilin University,Changchun,130012)
(4.School of Mathematics,Jilin University,Changchun,130012)
Generalized Extended tanh-function Method for Traveling Wave Solutions of Nonlinear Physical Equations
CHANG JING1,GAO YI-XIAN2,3AND CAI HUA4,*
(1.Fundamental Department,Aviation University of Air Force,Changchun,130022)
(2.College of Mathematics and Statistics,Northeast Normal University, Changchun,130023)
(3.Key Laboratory of Symbolic Computation and Knowledge Engineering of Ministry of Education,Jilin University,Changchun,130012)
(4.School of Mathematics,Jilin University,Changchun,130012)
Communicated by Li Yong
In this paper,the generalized extended tanh-function method is used for constructing the traveling wave solutions of nonlinear evolution equations.We choose Fisher’s equation,the nonlinear schr¨odinger equation to illustrate the validity and advantages of the method.Many new and more general traveling wave solutions are obtained.Furthermore,this method can also be applied to other nonlinear equations in physics.
generalized tanh-function method,nonlinear Schr¨odinger equation, Fisher’s equation
1 Introduction
It is well known that the nonlinear phenomena is very important in variety of the scienti fi c fi elds,especially in fl uid mechanics,solid state physics,plasma physics,plasma waves, capillary-gravity waves and chemical physics.Most of these phenomena are described by the nonlinear partial di ff erential equations.So exact solutions of the nonlinear partial di ff erential equations play an essential role in the nonlinear science.For this end,various methods,such as the inverse scattering method(see[1]),the Hirota’s bilinear technique(see[2]), and truncated Painl´ve expansion(see[3])have been developed to obtain exact solutions. The tanh method presented by Mal fl iet[4–6]is a powerful solution method to get the exact traveling wave solutions.Later,Fanet al.[7–8]proposed an extended tanh-function method and obtained the new traveling wave solutions which cannot be obtained by tanh-function method.Recently,El-Wakil and Abdou[9]modi fi ed the extended tanh-function method and obtained some new exact solutions.In this paper,we extended the modi fi ed tanh-function method to get the new exact traveling wave solutions.For illustration,we apply this method to Fisher’s equation and the nonlinear Schr¨odinger equation with general nonlinearity.
2 The Generalized Extend tanh-function Method
In this section,we give a brief description of the generalized extended tanh method.Consider the following nonlinear partial di ff erential equation(PDE):
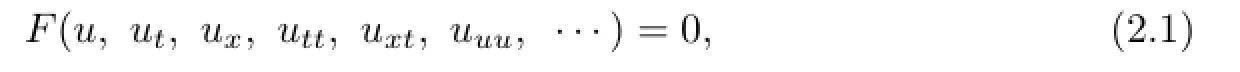
where u=u(t,x)is an unknown function,F is a polynomial in u=u(t,x)and its various partial derivatives,in which the highest order derivatives and nonlinear terms are involved.
We fi rst consider the traveling wave solutions of(2.1)
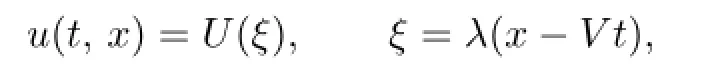
and reduce(2.1)into the following ordinary di ff erential equation(ODE):
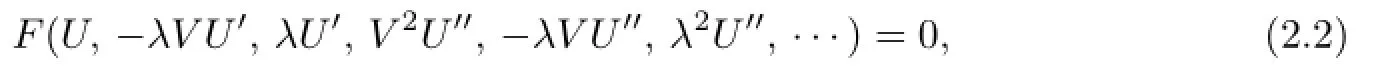
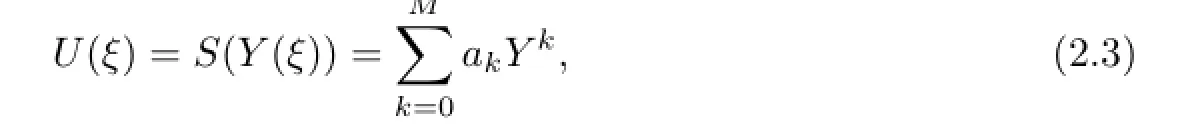
where the positive integer M can be determined by balancing the highest order derivative term with the nonlinear terms in(2.2),and Y is the solution of the Riccati equation

where α and b are constants to be determined.Substituting(2.3)and(2.4)into(2.2)and equating the coefficients of all powers Ykto zero yield a system of algebraic equations for V,λ,a0,ai(i=1,2,···),from which the constants are obtained explicitly.
The Riccati equation(2.4)has general solutions as follows:
(I)If α=0 and b=−1,then
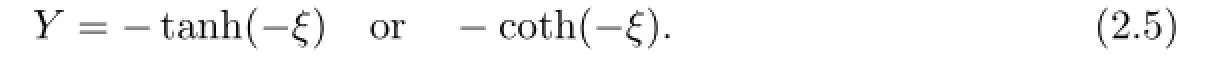
This method is the traditional tanh method(see[4–6]).
(II)If α=0 and b is an arbitrary constant,then
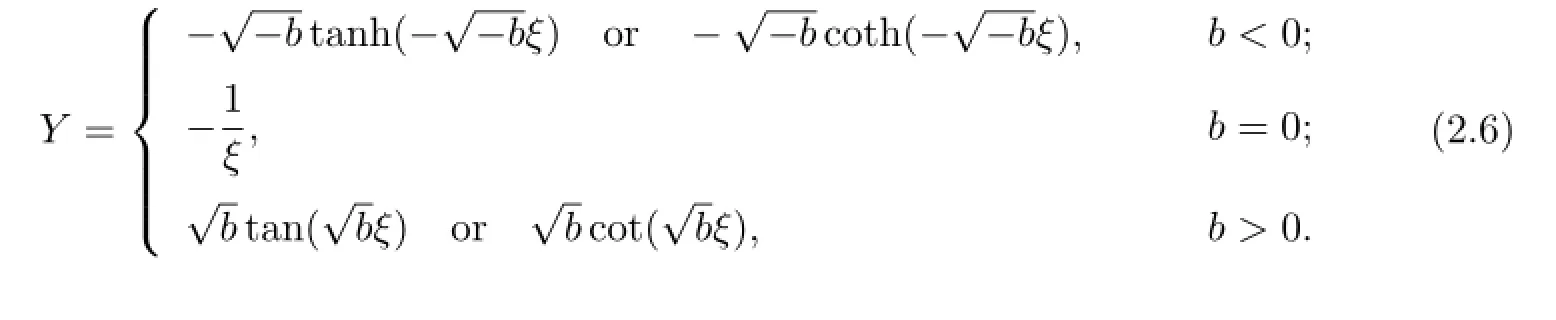
This method is the extended tanh-function method(see[7–9]).
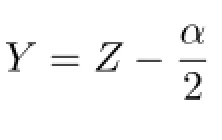

Thus the solutions of(2.4)are
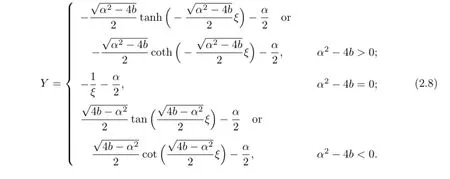
3 Applications
3.1 Fisher’s Equation
We consider the generalized Fisher’s equation

and look for the traveling wave solution

Then(3.1)is transformed into the following ODE:

Substituting(2.3)and(2.4)into(3.2),we can get
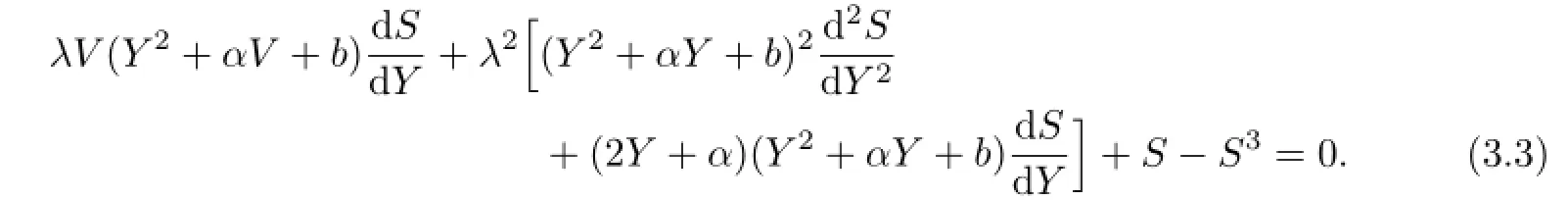
To determine the parameter M we usually balance the linear terms of highest order in the resulting equation(3.3)with the nonlinear terms of highest order.Thus we get

Write
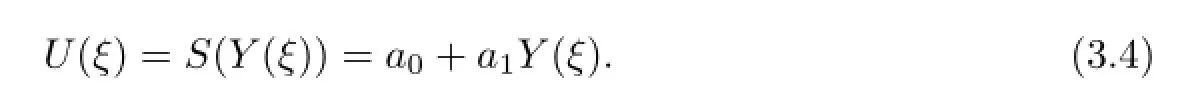
Substituting(3.4)into(3.3),we have the algebraic equation with respect to V,λ,a0,a1,as follows:
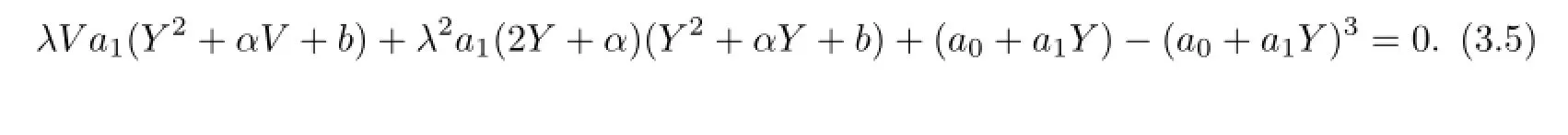
So we get
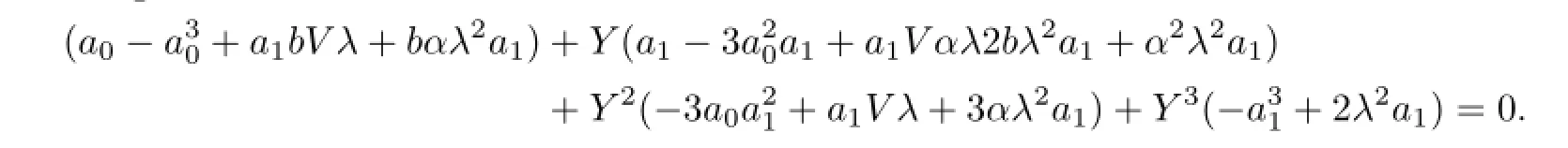
Equating each coefficient of this polynomial to zero,we obtain the following system of the algebraic equations with respect to V,λ,a0,a1,α,b:
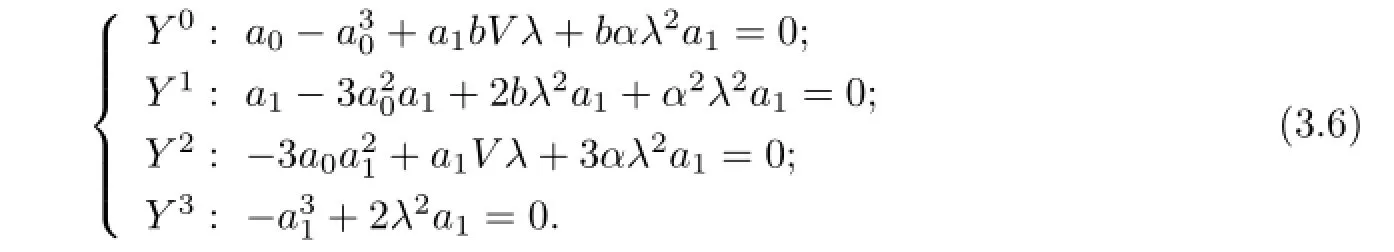
(I)If α=0 and b=−1,with the aid of Mathematica,we get the solutions of(3.6):
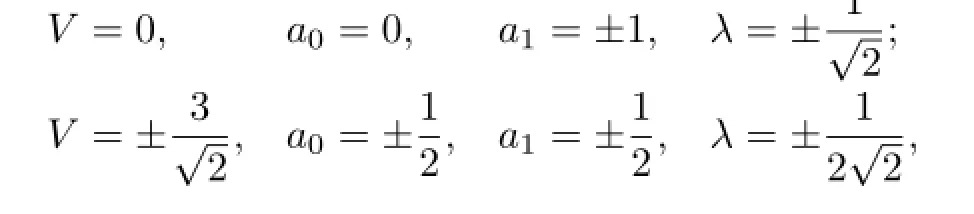
with
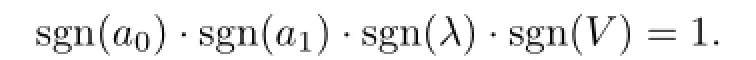
So,according to(2.5),we get the solutions of(3.1)as follows(see[10]):
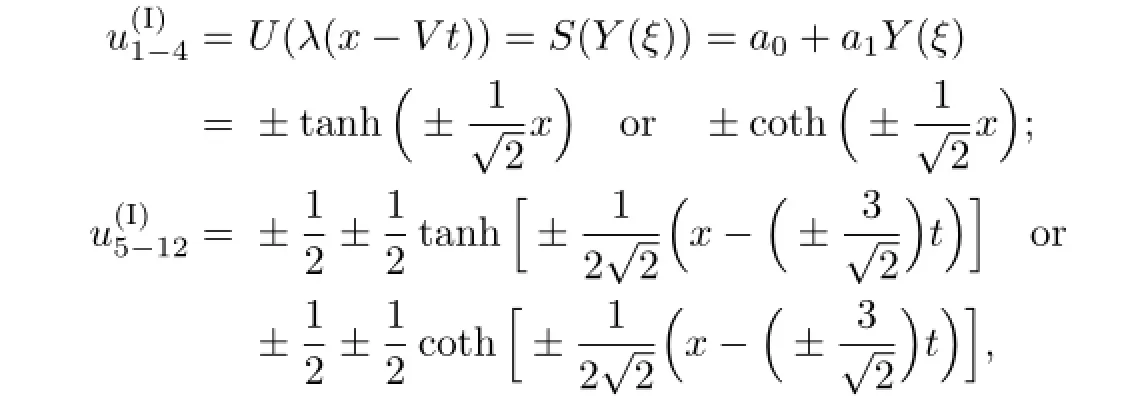
with
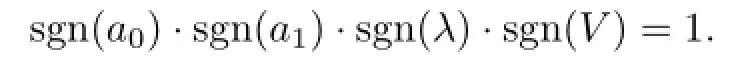
(II)If α=0 and b is an arbitrary constant,then the method is the modi fi ed extended tanh-function method.With the aid of Mathematica,we get the solutions of(3.6):
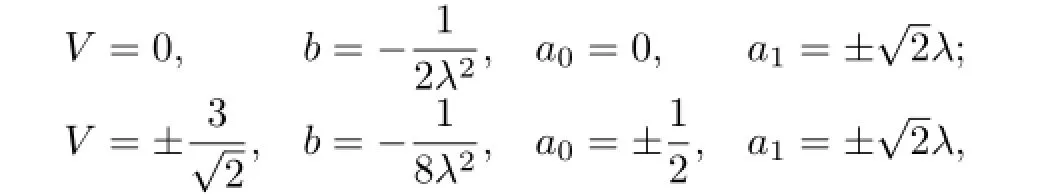
with
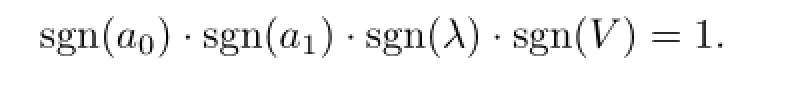
Obviously,when b<0,according to(2.5),we get the solutions of(3.1)as follows:

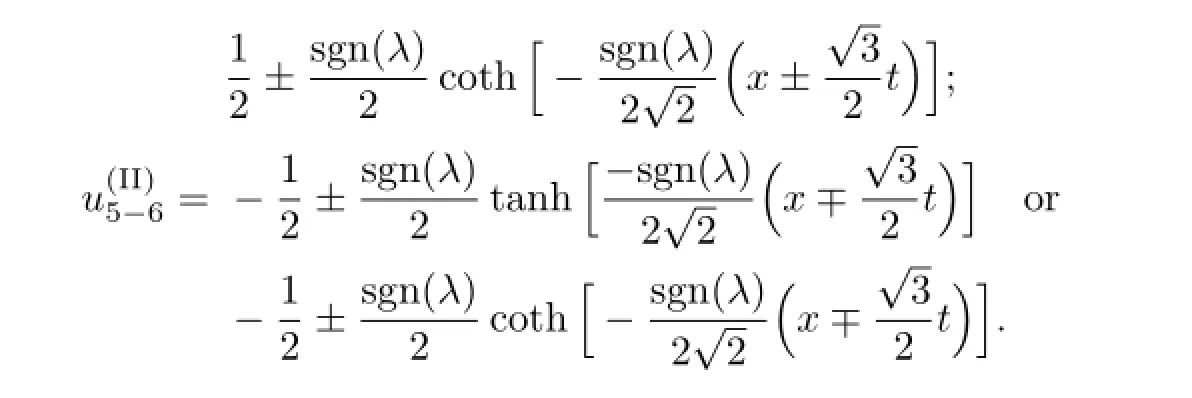
(III)(i)When α2−4b=0,α̸=0,with the aid of Mathematica,we obtain the solutions of(3.6)as follows:
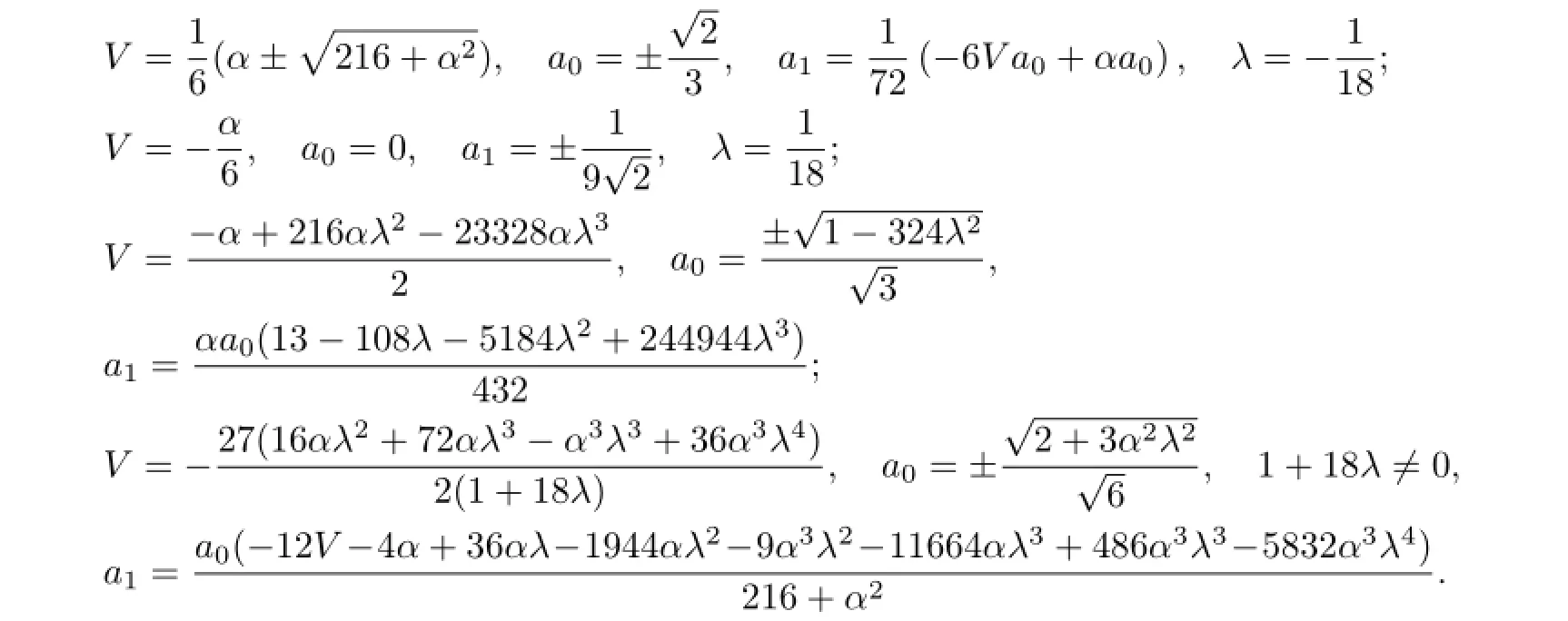
According to(2.8),we obtain the solutions of(3.1):
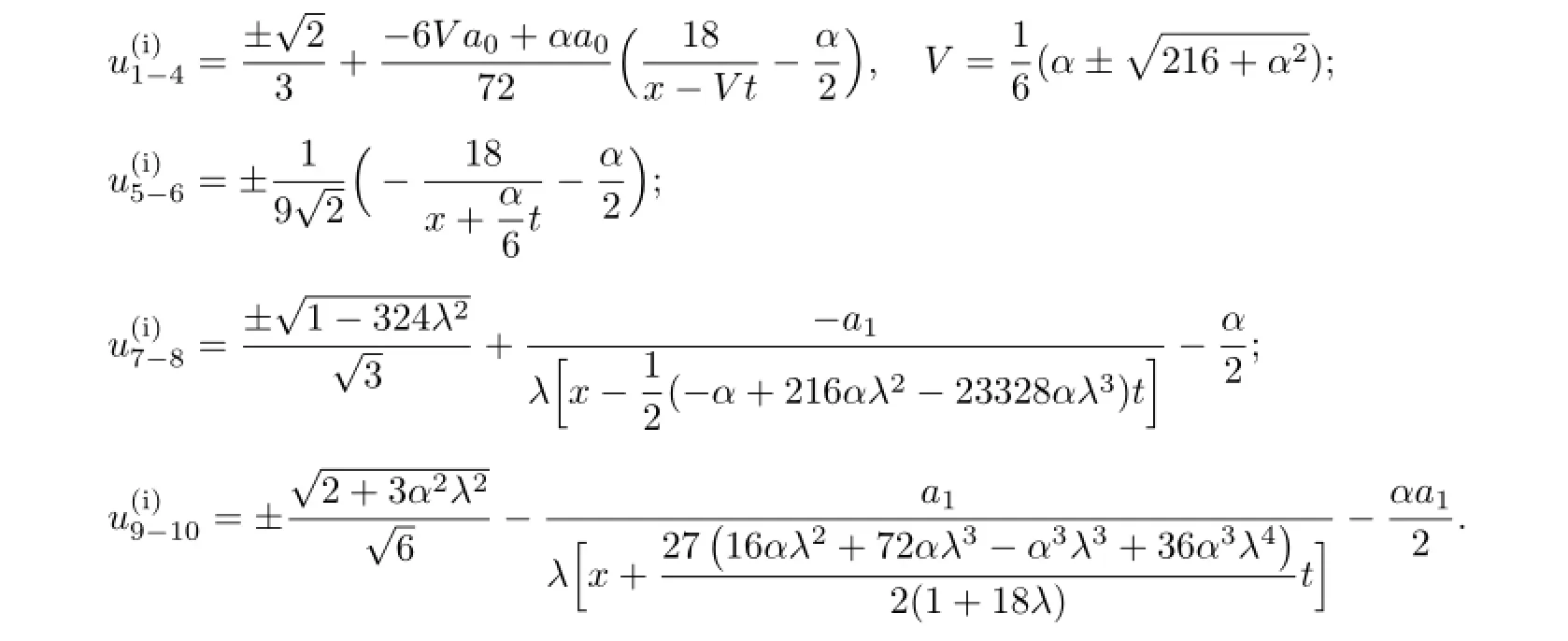
(ii)When α2−4b=0 and α̸=0,with the aid of Mathematica,we get the solutions as follows:
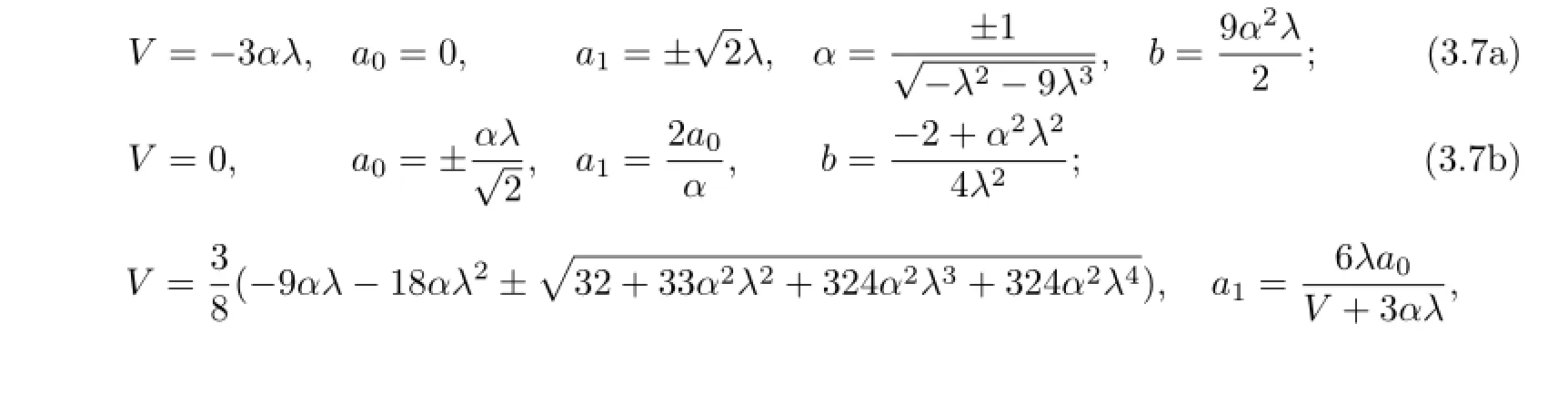
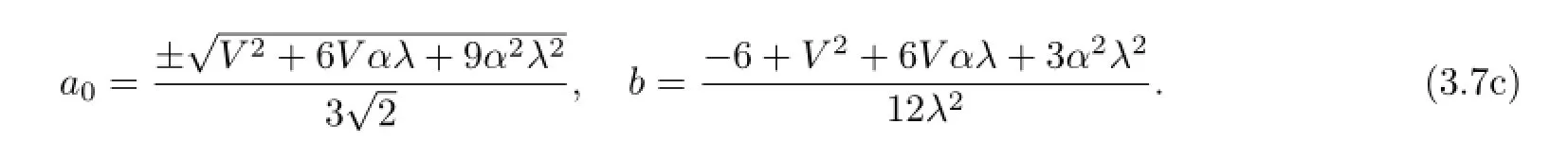
Obviously,from(3.7a)we have
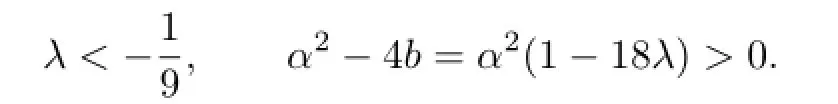
So,according to(2.8),we have the exact traveling wave solutions of(3.1)as follows:

From(3.7b)we have α2−4b=2>0.The traveling wave solutions of(3.1)are
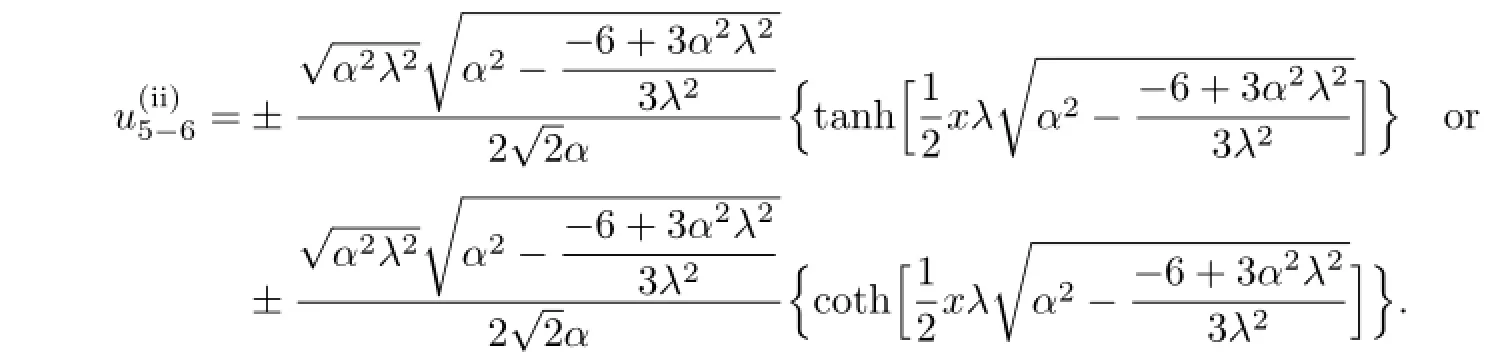
So,if 6−V2−6V αλ>0,then we get the solutions of(3.1)as follows:
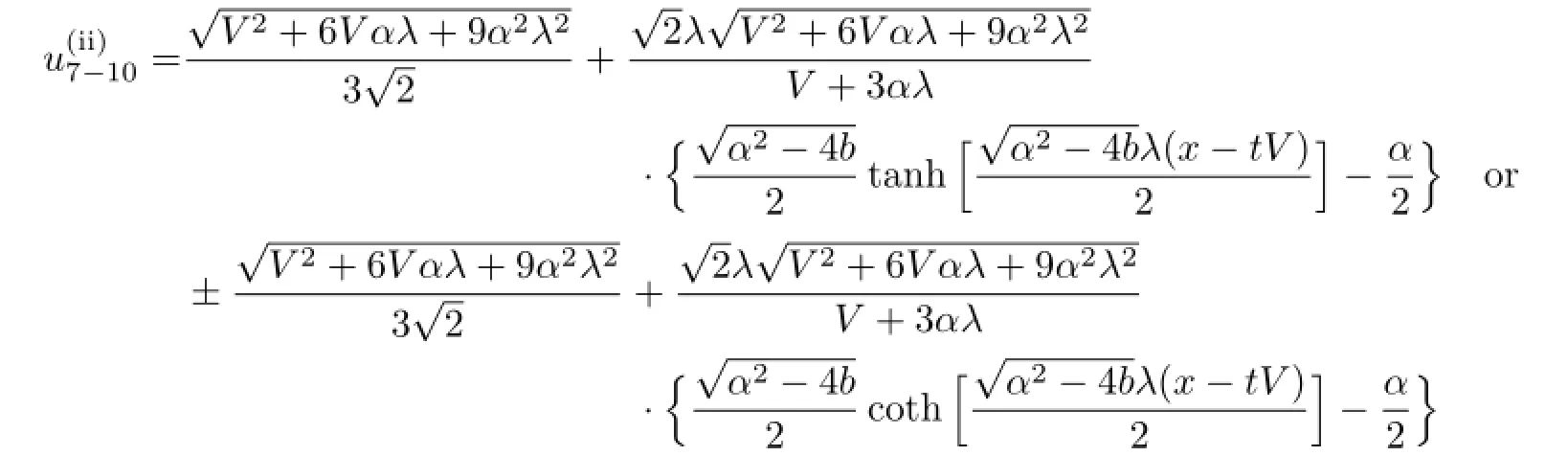
with
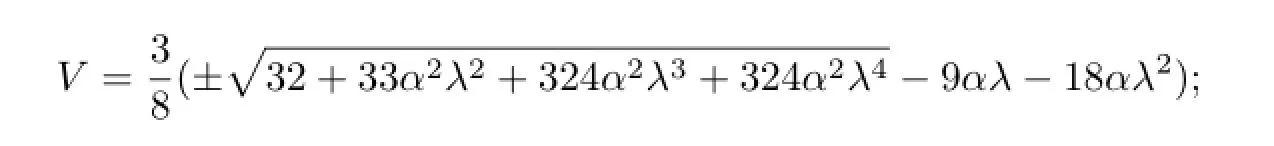
if 6−V2−6V αλ<0,then the traveling wave solutions of(3.1)are

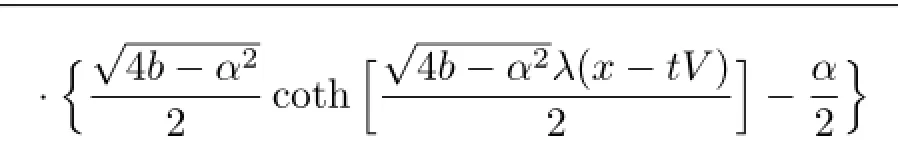
with the same velocity as above.
3.2 The Nonlinear Schr¨odinger Equation
We consider the nonlinear Schr¨odinger equation
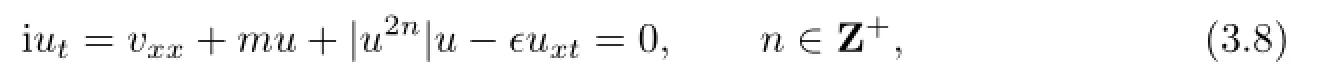
where u(t,x)is a complex function,and m,ϵ∈Rare constants.We assume that

where U(t,x)is a real function,µand ν are constants to be determined.Substituting(3.9) into(3.8),removing the common factor ei(µx+νt)and separating the real and imaginary parts,we have the following PDEs of U(t,x): {
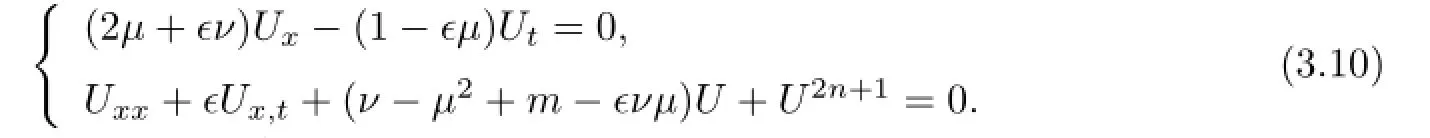
(I)When n=1,we look for the traveling wave solutions
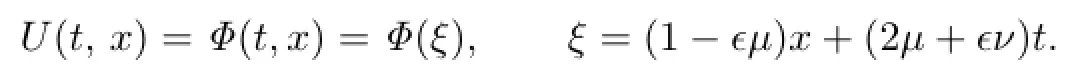
Then(3.10)becomes
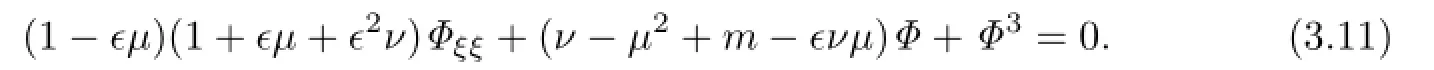

Balancing the linear term of the highest order with the nonlinear term yields M=1. Therefore,we getΦ(ξ)=a0+a1Y.Substituting it into the above equation,we get the system of algebraic equations with respect to a0,a1,µ,ν,α,b:
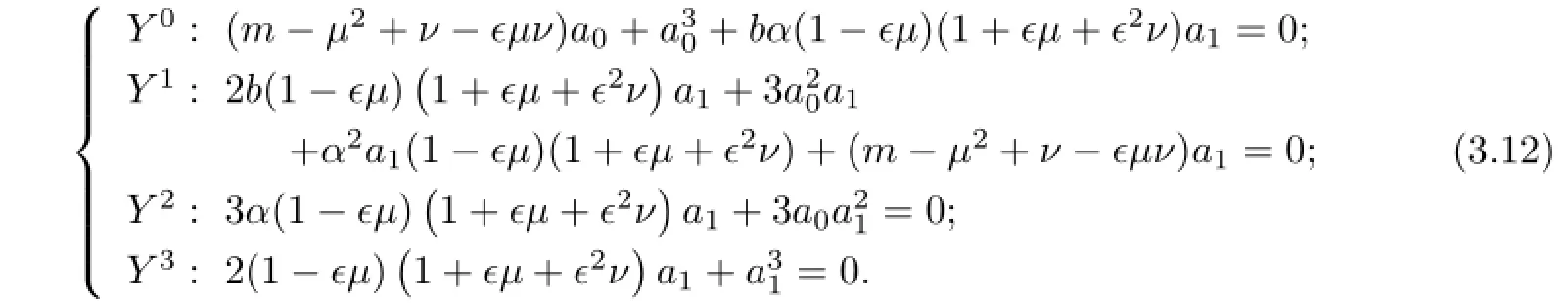
(i)When α=0 and b=−1,with the aid of Mathematica,we get the solutions of(3.12):
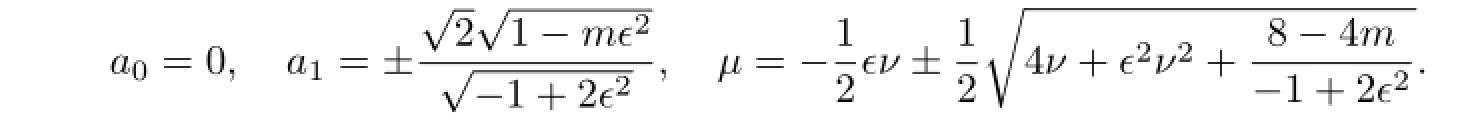
So,by the traditional tanh method,we can get the traveling wave solutions of(3.8):
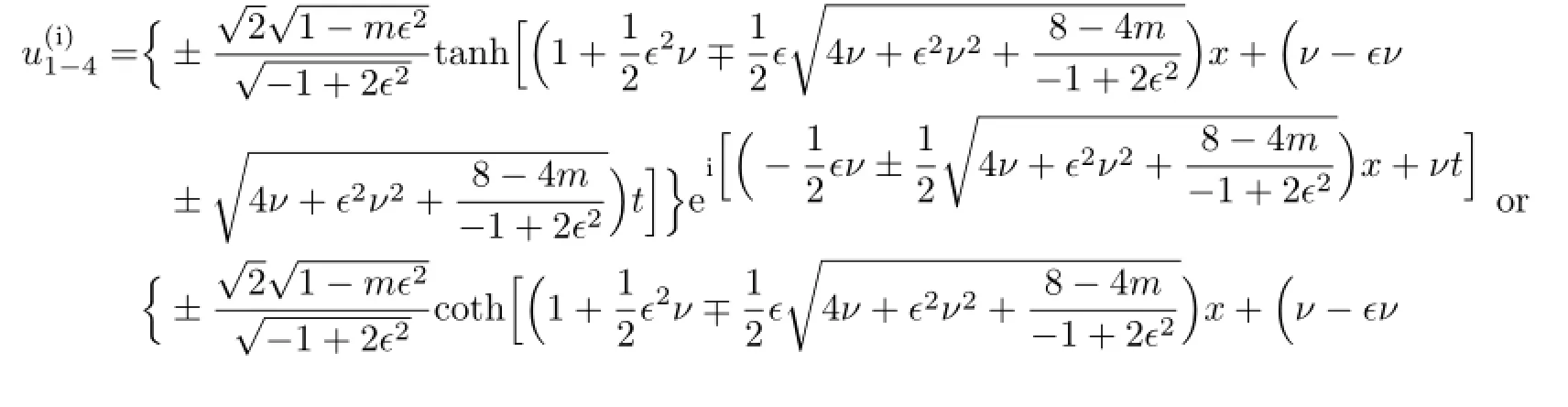
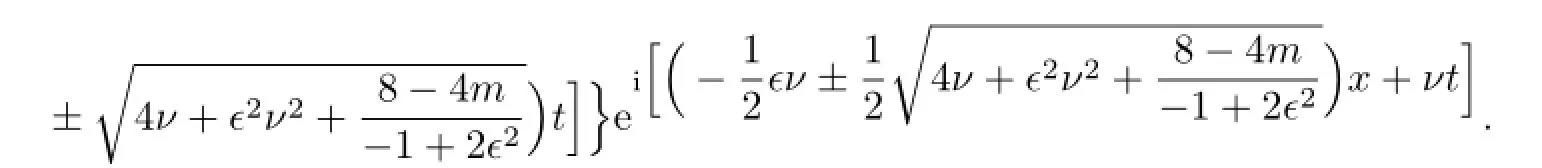
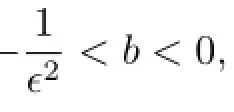
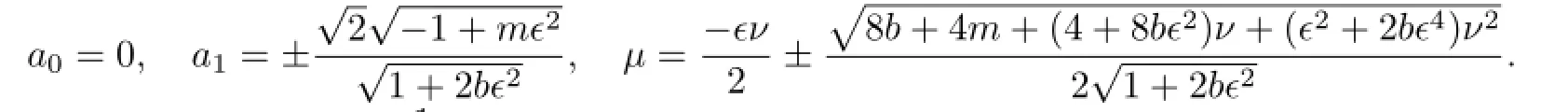

If b=0,then the solutions of(3.8)are
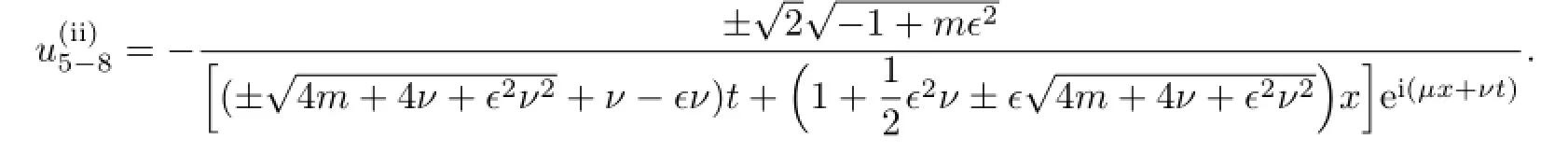
If b>0,then the traveling wave solutions of(3.8)are
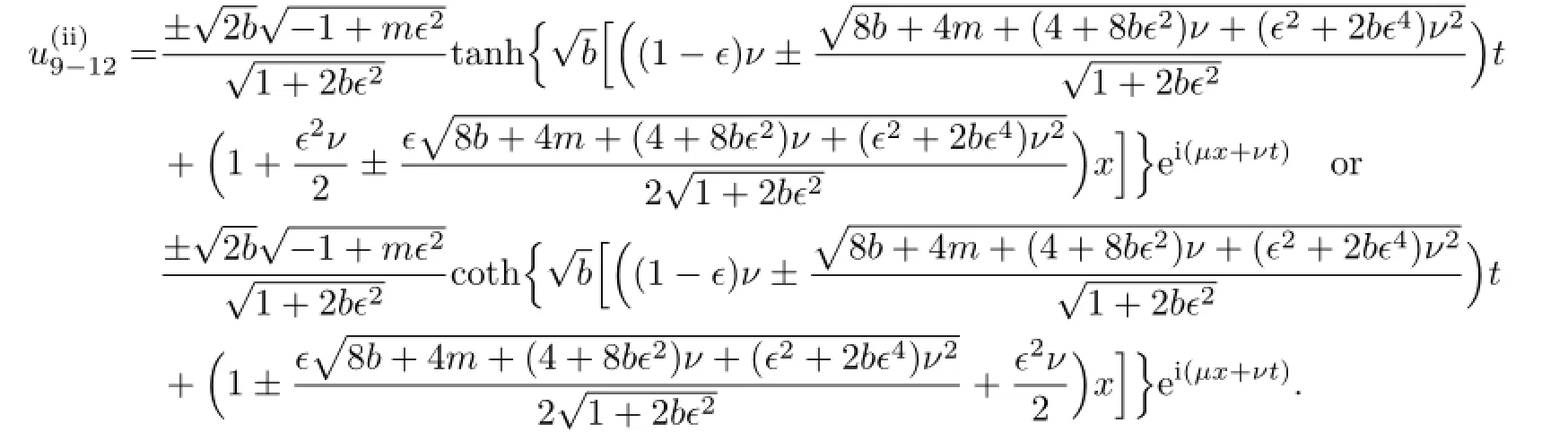
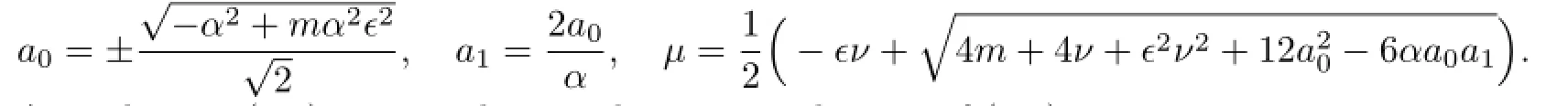
According to(2.8),we get the traveling wave solutions of(3.8):
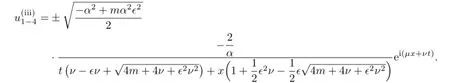
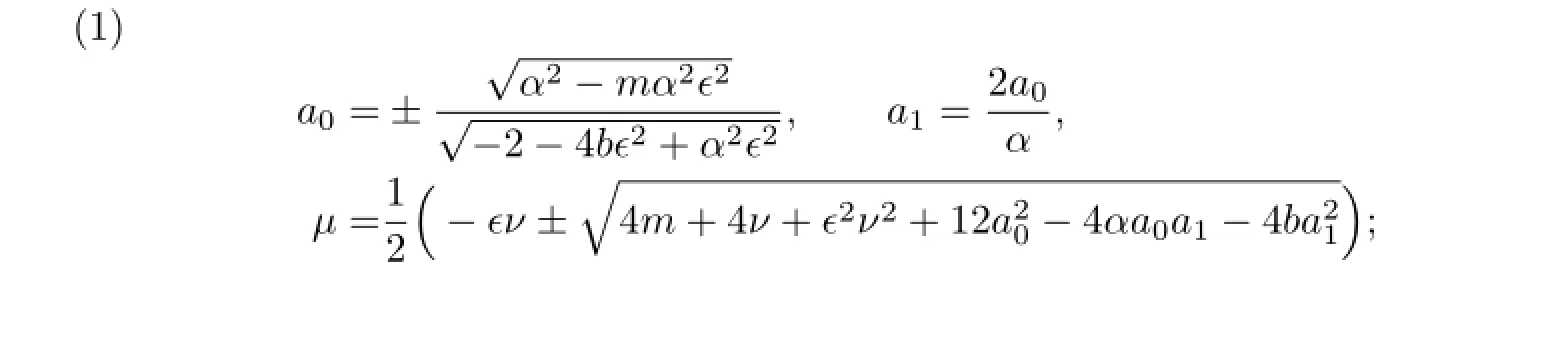
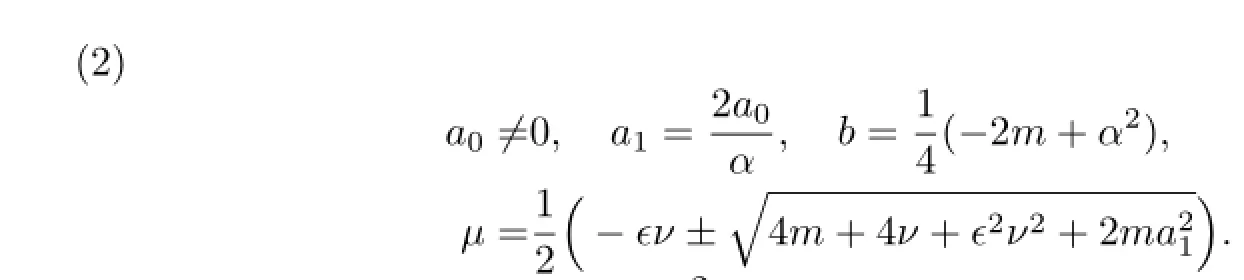
Obviously,in(1)we have α2−4b>
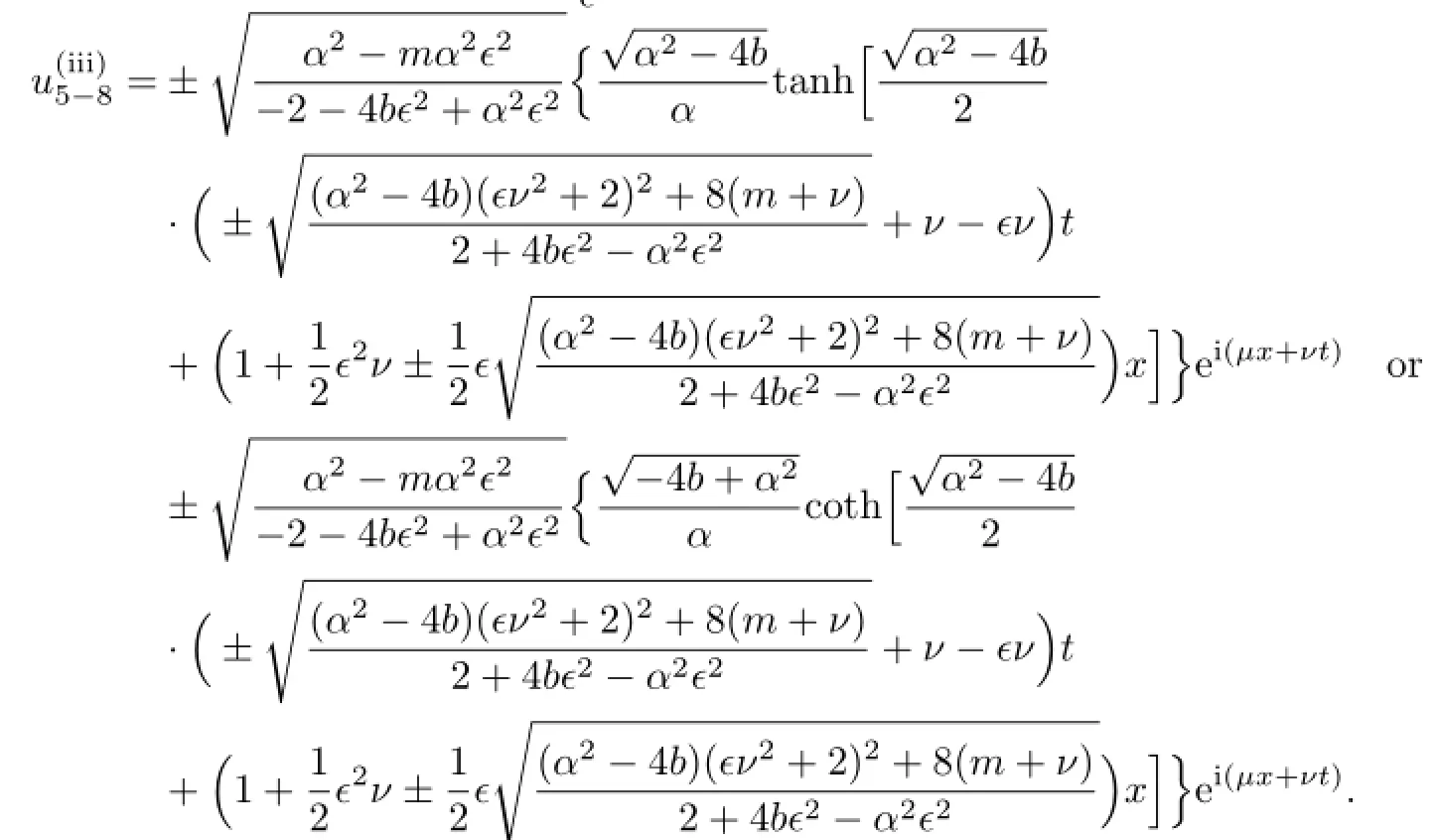
>0.So the traveling wave solutions of(3.8)are
In(2),we have α2−4b=2m.So,if m>0,we can get the solutions of(3.8)
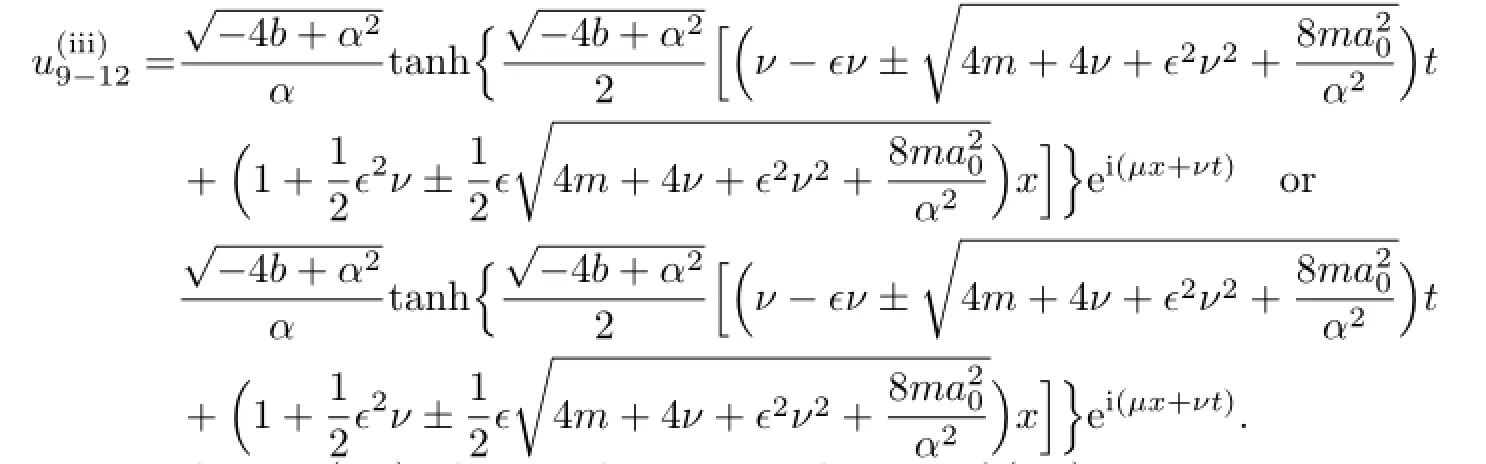
If m<0,according to(2.8),the traveling wave solutions of(3.8)are
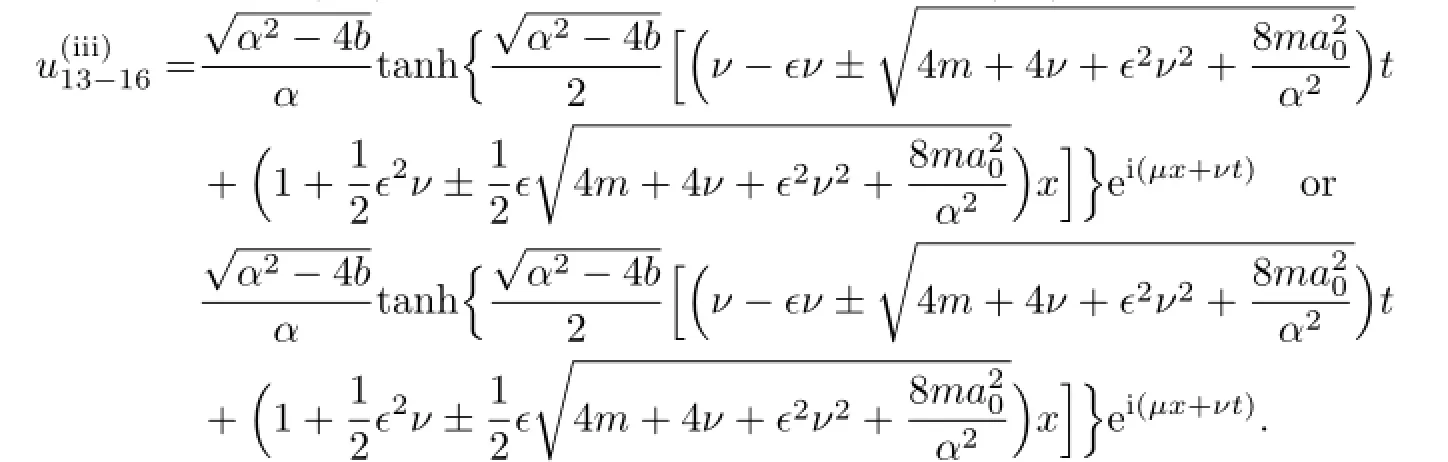
(II)When n>1,if we proceed as presented above,we fi nd M=
This means that the tanh method is not appropriate for any positive integer n≥2.In order to use the method, we make the following transformation as that in[10]:
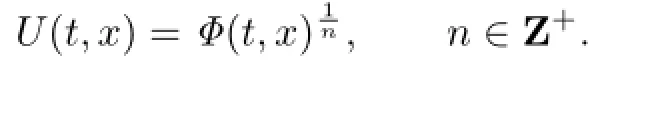
Then(3.10)is changed into
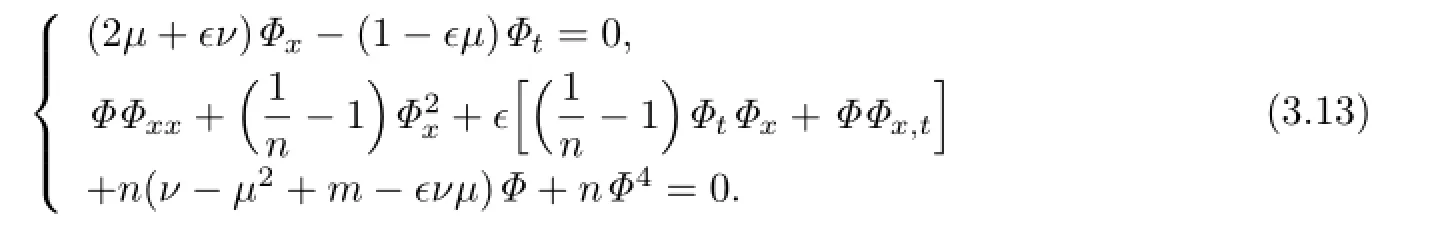
Assume that the traveling wave solutions of(3.13)have the form
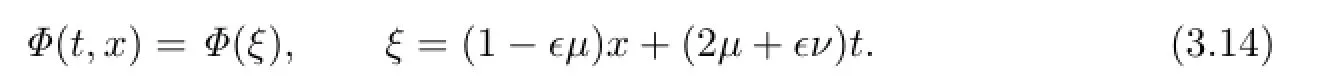
Substituting(3.14)into(3.13),we get

According to(2.3),we assume that
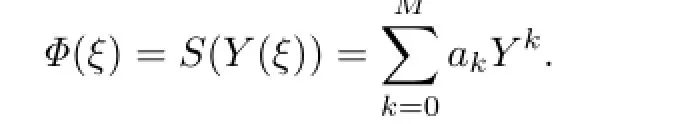
Substituting(2.4)into(3.15),we can get
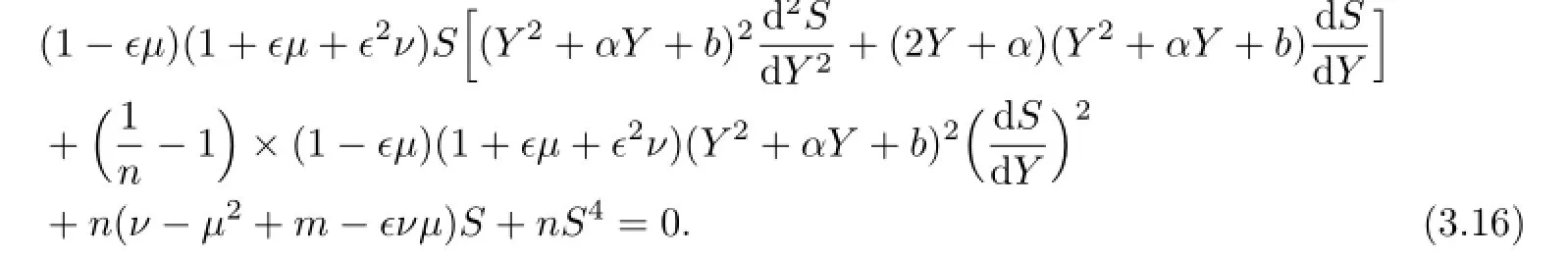
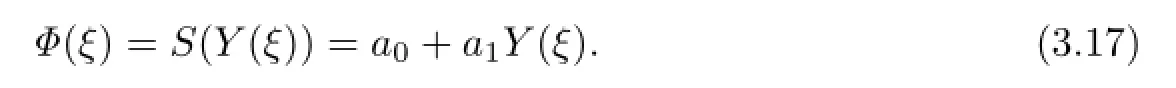
Substituting(3.17)into(3.16),we can get the system of the algebraic equation with respect to a0,a1,ν,µ:
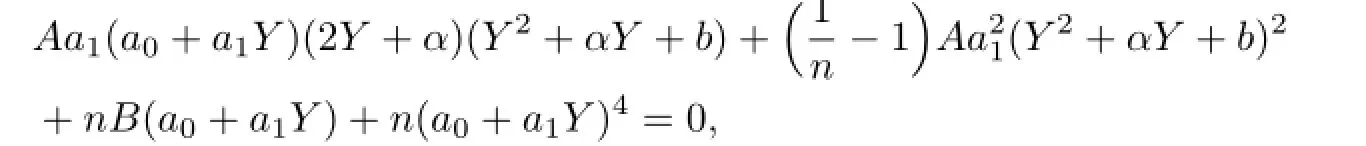
with

Equating each coefficient of this polynomial in Y to zero,we obtain the following system of the algebraic equations:
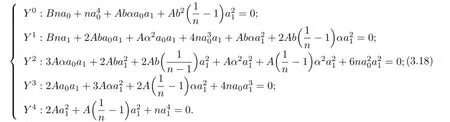
(i)When α=0 and b=−1,there are no non-trivial solutions of(3.18).
(ii)When α=0 and b is an arbitrary constant.If b=0,with the aid of Mathematica, we get the solutions of(3.18)
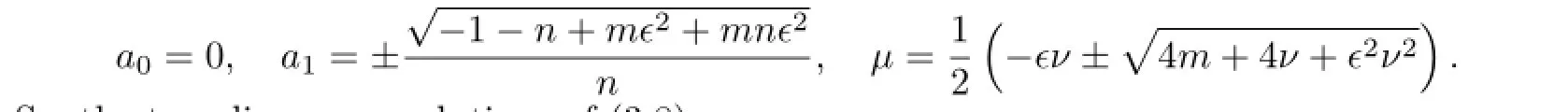
So,the traveling wave solutions of(3.8)are
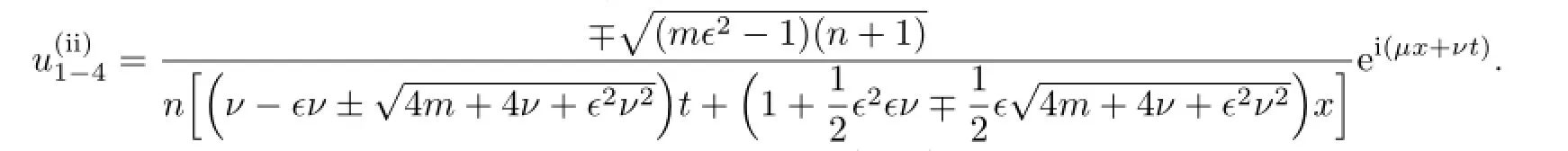
If b=0,then there are no non-trivial solutions of(3.18).
(iii)When α̸=0,with the help of Mathematica,there are no non-trivial solutions of (3.18).
4 Conclusion
In this paper,we have applied the generalized tanh method to construct a series of traveling wave solutions for some special types of equations:Fisher’s equation and the nonlinear Schr¨odinger equation.These traveling wave solutions are expressed in terms of hyperbolic tangent(cotangent),trigonometric and rational functions depending on di ff erent parameters. The performance of the generalized tanh method is direct,concise and e ff ective.This method will be used in further works to establish more and new solutions of many other nonlinear evolution equations.
[1]Ablowitz M J,Clarkson P A.Solitons,Nonlinear Evolution and Inverse Scattering.Cambridge: Cambridge Univ.Press,1991.
[2]Gu C H.Soliton Theory and Its Application.Berlin:Springer,1995.
[3]Tian B,Gao Y.Truncated Painlev´e expansion and a wide-ranging type of generalized variablecoefficient Kadomtsev-Petviashvili equations.Phys.Lett.A,1995,209:297–304.
[4]Mal fl iet W.Solitary wave solutions of nonlinear wave equations.Amer.J.Phys.,1992,60(7): 650–654.
[5]Mal fl iet W.The tanh method:I.Exact solutions of nonlinear evolution and wave equations. Phys.Scripta,1996,54:563–568.
[6]Mal fl iet W.The tanh method:II.Perturbation technique for conservative systems.Phys. Scripta,1996,54:569-575.
[7]Fan E.Extended tanh-function method and its applications to nonlinear equations.Phys.Lett. A,2000,277:212–218.
[8]Fan E,Hon Y C.Generalized tanh method extended to special types of nonlinear equations. Z.Naturforsch,2002,57a:692–700.
[9]El-Wakil S A,Abdou M A.New exact travelling wave solutions using modi fi ed extended tanhfunction method.Chaos Solitons Fractals,2007,31:840–852.
[10]Wazwaz A M.The tanh method for travelling wave solutions of nonlinear equations.Appl. Math.Comput.,2004,154(3):713–723.
tion:34N05
A
1674-5647(2014)01-0060-11
Received date:Sept.15,2011.
Foundation item:The NSF(11001042)of China,SRFDP(20100043120001)and FRFCU(09QNJJ002).
*Corresponding author.
E-mail address:changjing81@126.com(Chang J),caihua@jlu.edu.cn(Cai H).
杂志排行
Communications in Mathematical Research的其它文章
- Existence of Solutions to Generalized Vector Quasi-variational-like Inequalities with Set-valued Mappings
- Some Notes on Normality Criteria of Meromorphic Functions
- Variational Approach to Scattering by Inhomogeneous Layers Above Rough Surfaces
- T∗-extension of Lie Supertriple Systems
- Complete Convergence of Weighted Sums for Arrays of Rowwise m-negatively Associated Random Variables
- Co fi niteness of Local Cohomology Modules with Respect to a Pair of Ideals
