改进遗传K 均值算法在负荷特性分类的应用

黄毅成，杨洪耕

（四川大学电气信息学院，成都610065）

近年来，随着电网需求侧负荷特性多样化以及电网复杂程度的提高，使得对综合负荷特性建立完全精确的数学模型变得十分困难[1]，需要对负荷进行分类和综合，从而建立一定精确程度的负荷模型[2]，其中，负荷特性的聚类分析是负荷建模的基础工作。精确的负荷特征分类对电网规划、实时调度和运行规划等具有重要的现实意义。

负荷建模为电网规划、运行规划、调度等提供有效的数学参考模型，随着负荷建模的研究深入，负荷特性的分类越来越受到重视。文献[3]应用基于模糊矩阵和模糊C 均值方法对负荷特征进行聚类，但模糊矩阵聚类精确度低，而且模糊C 均值算法对中心敏感，易陷入局部最优；文献[4-5]提出对模糊C 均值方法的改进，而如何确定最优聚类数目问题依然存在；文献[6]提出改进的K 均值聚类方法，针对聚类中心敏感和聚类数目确定提出改进，但数据量增大时，精确性会降低；文献[7]提出一种应用KOHONEN 神经网络解决负荷动特性聚类的方法；文献[8]采用灰色关联度聚类，基于统计学方法，需要对实地负荷进行调查统计，工作量大，不利于推广。上述方法对负荷聚类精度有一定提高，但由于负荷特征存在随机性，分散性和最优聚类数目确定和聚类中心选择是目前研究所重视的问题。

本文提出一种改进遗传算法，利用K 均值的局部搜索能力和遗传算法[9]的全局搜索能力，以万安变电站220 kV 侧有功无功电压96 个实测数据作为负荷特征量进行聚类分析。相比于其他聚类方法，本文在利用遗传算法搜索最优聚类中心的同时，采用可变长编码方案，让聚类数目自动变化，动态寻优，以取得更好的聚类效果。仿真实例结果显示本文方法有效提高了分类的准确性。

1 负荷模型

负荷模型的精确性是建立在负荷特征分类准确的基础上，即负荷建模的准确性直接反映了负荷分类的准确性。本文采用静态负荷模型对分类负荷特征进行综合分析，具体表达式为

式中：U 为实际电压；U0为基值电压；P、Q 分别为端电压为实际电压U 时负荷吸收的功率；P0、Q0分别为端电压为基值电压U0时负荷吸收的功率；系数a、b、c 为各类负荷所占百分比，有

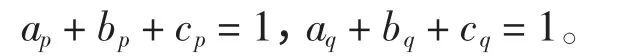
定义拟合误差e 为

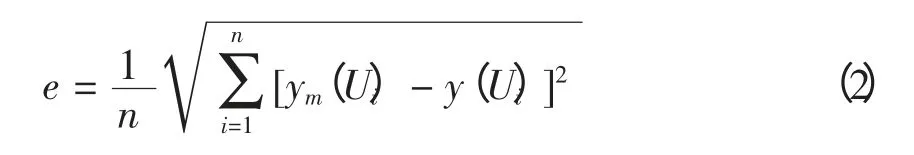
式中：ym（Ui）为模型有功无功响应；y（Ui）为实测有功无功数据；Ui为第i 个样本数据电压值。

2 算法实现过程

2.1 可变长编码遗传K 均值算法聚类

将遗传算法用于聚类分析中，并在种群进化过程中引入了K 均值算法操作[10]。

2.1.1 负荷特征选择及编码方案

在聚类问题中，聚类中心往往难以确定，因此采用动态方式确定聚类中心，相应的染色体采用可变长编码方案[11]。

本文采用万安变电站1 周内96 个数据作为负荷特征样本数据进行编码，染色体的基因由初始聚类中心对应的样本数据直接表示，其编码形式为

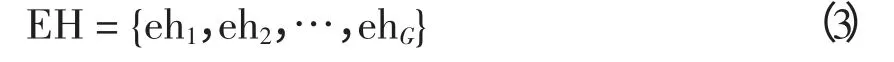
式中：EH为染色体种群；G 为种群数；ehi为第i 条染色体；L 为染色体长度，不同染色体长度不同；T为初始聚类中心对应的负荷特征样本数据。长度为5 的染色体ehi如图1 所示。

2.1.2 适应度函数

由于染色体编码采用的是可变长的编码方式，那么聚类中心的数目并不固定，其适应度函数与定长编码时的适应度函数有所区别，即

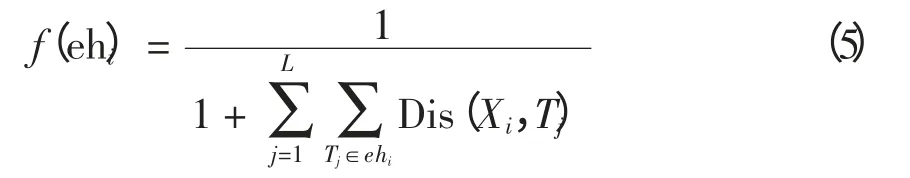
式中，Xi为染色体ehi中心。通过计算该类负荷特征Tj到中心的距离总和，就可得到各类的适应度值，进而求得染色体ehi的适应度。

2.1.3 种群初始化

由于染色体长度可变，因此种群初始化的方法具有一些自身的特点。随机设置染色体的长度L为聚类数的经验值）。随机从N个样本中选取M 个样本形成一条染色体，重复G次，形成规模为G 的种群。

2.1.4 遗传算子

1）选择算子

用适度比例法与精英个体保存相结合的混合选择算子选择进行交叉和变异的染色体。在每一步的迭代中，选出适应度最高的n 个染色体作为精英个体直接进入下一代；再用适度比例法选出优秀个体进入下一代，染色体ehi被选中的概率为

2）插入删除交叉算子具体操作

针对采用的可变长染色体编码，设计插入删除交叉算子。插入删除交叉算子的主要思想是将一个染色体的一段基因删除，并将这段基因插入另一个染色体的某一个位置，再对染色体进行重复基因删除操作，即

图1 染色体编码Fig.1 Chromosome encoding

式中，d 为同一条染色体中两基因的距离。当d 小于5 时，则判定两基因相似。若染色体超长，则进行截尾操作，具体操作如图2 所示。

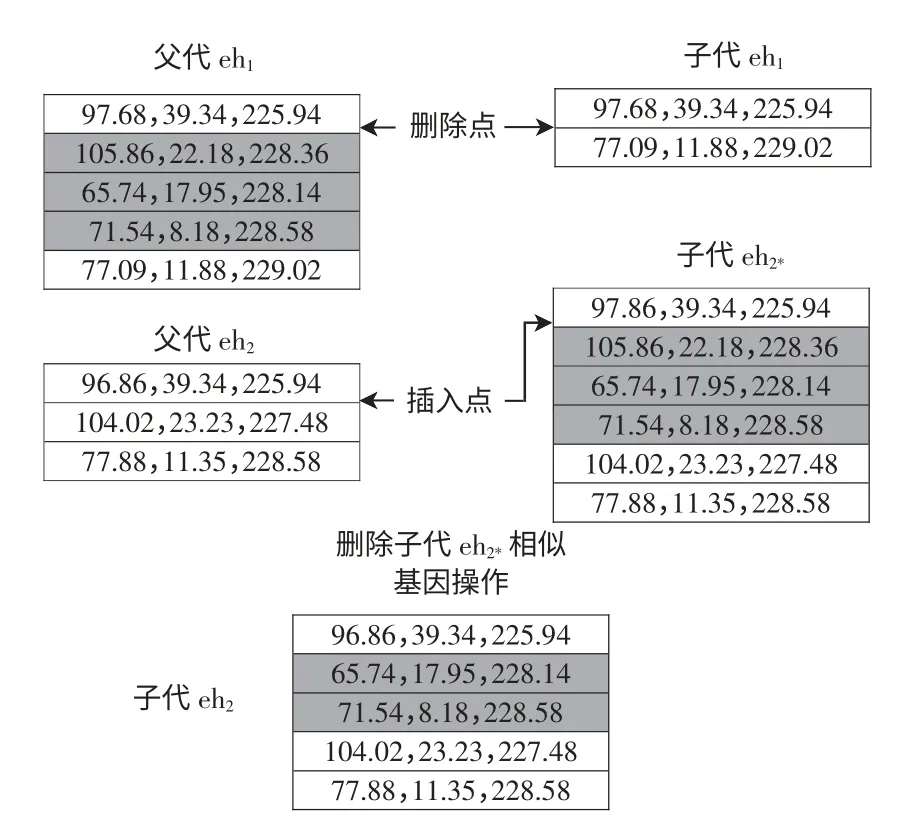
图2 插入删除操作Fig.2 Insertion and deletion operation

3）变异操作

随机产生一个介于[1，L]之间的自然数I，将I作为变异点个数；从i=1 开始，随机生成一个介于[0，1]之间的自然数r。若r ≤Mm（变异概率），则不进行变异操作；否则随机生成一个介于[1，N]之间的自然数，用该自然数对应的样本负荷特征数据替换父代染色体中的数据；置i=i+1，重复上述过程直到i>I，退出变异操作。

4）自适应交叉和变异概率

采用自适应遗传算子对交叉概率和变异概率进行调整，使得遗传算法具有更高的全局最优性和更快的收敛速度。

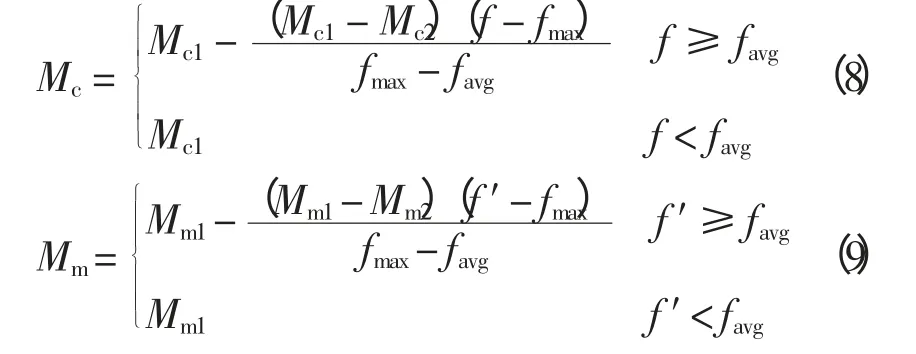
式中：fmax为当代群体中最大适应度值；favg为当代群体平均适应度值；f 为要进行交叉操作的两染色体中的较大适应度值；f′为要进行变异操作的染色体适应度。

2.1.5 K 均值操作

以产生的新群体的编码值为中心，把每个样本点分配到最近的类，形成新的聚类划分；再按照新的聚类计算聚类中心，取代原来的编码值。

K 均值算法具有较强的局部搜索能力，因此引入K 均值操作后，遗传算法的收敛速度可以大大提高。

2.1.6 循环终止条件

循环代数从0 开始，每循环1 次，代数加1。当前循环代数小于预先规定的最大循环代数，则继续循环；否则结束循环，或者适应度不发生变化，则同样跳出循环。

2.2 算法流程

改进遗传K 均值算法聚类流程如图3 所示。

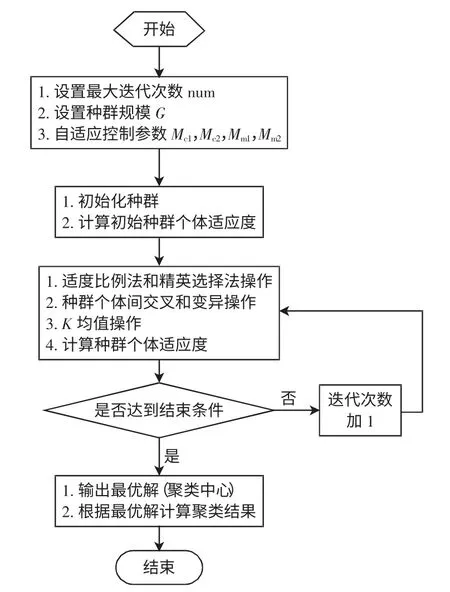
图3 改进遗传K 均值算法聚类流程Fig.3 Flow chart of clustering based on improved genetic and K-means algorithm

3 实例分析

采用万安220 kV 变电站220 kV 侧的96 个样本负荷特征数据，分别用K 均值算法、遗传算法以及改进遗传K 均值算法进行聚类分析。

首先在不确定聚类数的情况下，采用K 均值算法和遗传算法进行聚类，K 均值初始聚类中心确定为6，遗传算法采用定长染色体编码，且编码长度为6 对负荷特征进行聚类，聚类中心和样本编号如表1 和表2 所示。

算法参数设置如下：种群大小G=50，算法的最大迭代次数num=100，交叉概率Mc1=0.9，Mc2=0.62，变异概率Mm1= 0.1，Mm2= 0.01，精英个体数n =2，染色体最大长度L 设置为14，算法运行20次。得到的聚类结果如表3 所示。

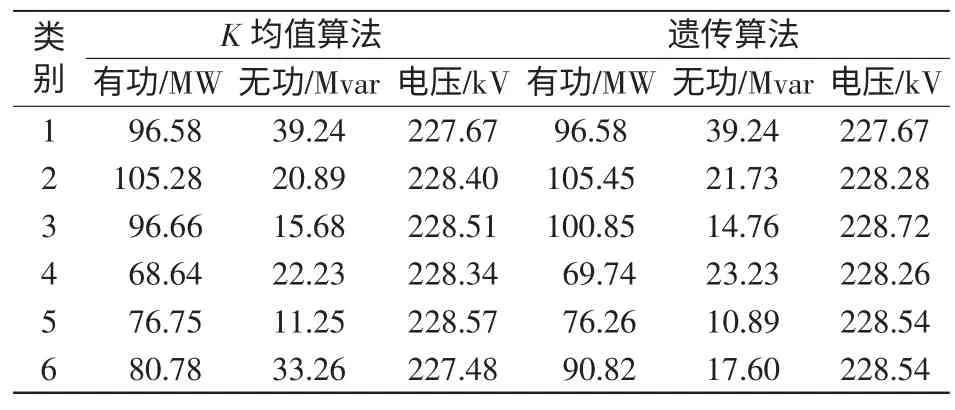
表1 K 均值算法和遗传算法聚类中心Tab.1 K-means and genetic algorithm clustering centers

表2 K 均值算法和遗传算法聚类结果Tab.2 K-means and genetic algorithm clustering results

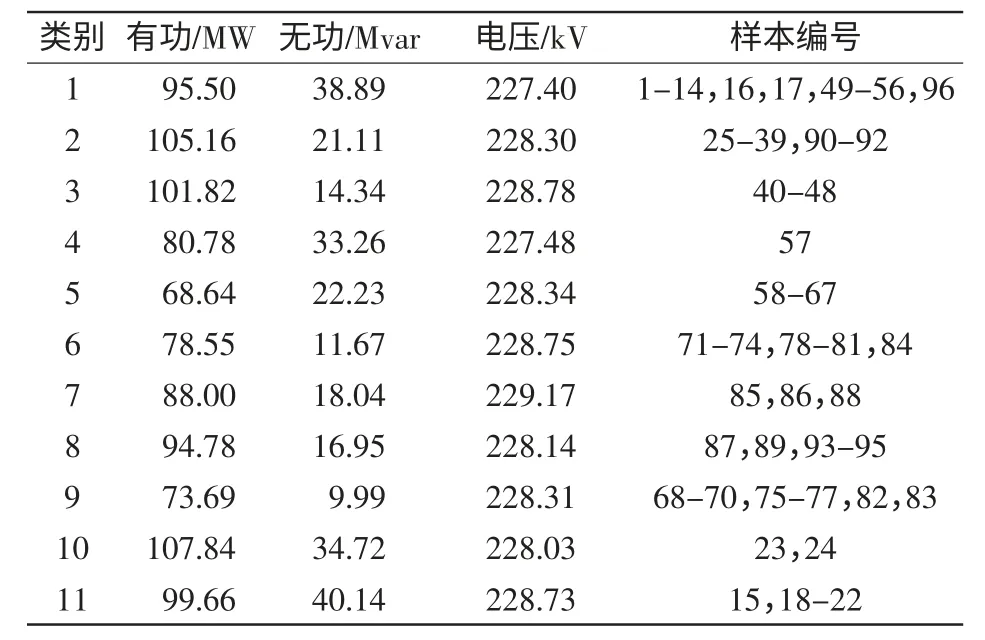
表3 改进遗传K 均值算法的聚类结果Tab.3 Clustering results of improved genetic and Kmeans algorithm

选取3 种方法中的相似类与第2 类负荷特征进行参数辨识，建立等效模型，并将聚类结果进行比较。第2 类负荷参数辨识结果见表4。

表4 第2 类参数辨识结果Tab.4 Results of 2nd parameters identifying

把第2 类负荷各样本的电压分别作用于等效模型，得到各类算法的拟合曲线，将有功功率拟合曲线进行比较，结果如图4～图6 所示。

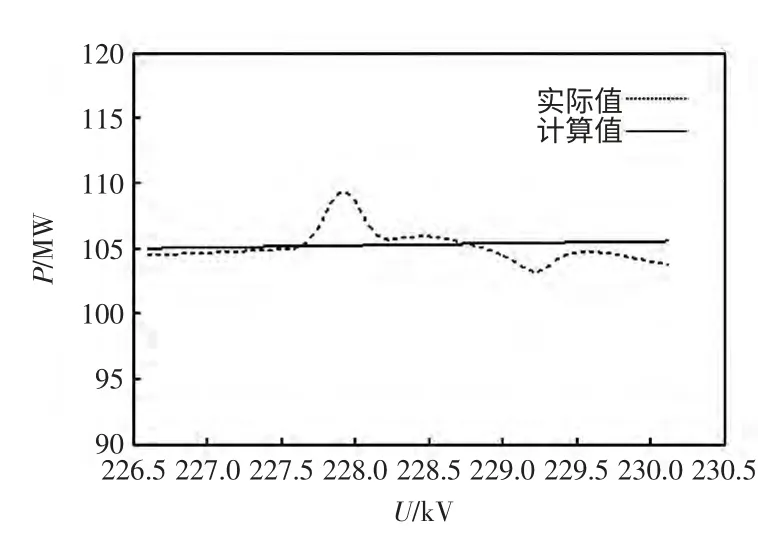
图4 K 均值算法的第2 类曲线拟合Fig.4 2nd clustering curves of K-means

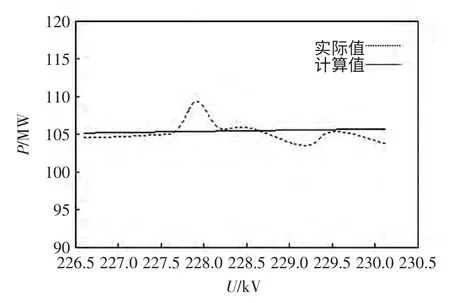
图5 遗传算法的第2 类曲线拟合Fig.5 2nd clustering curves of genetic algorithm

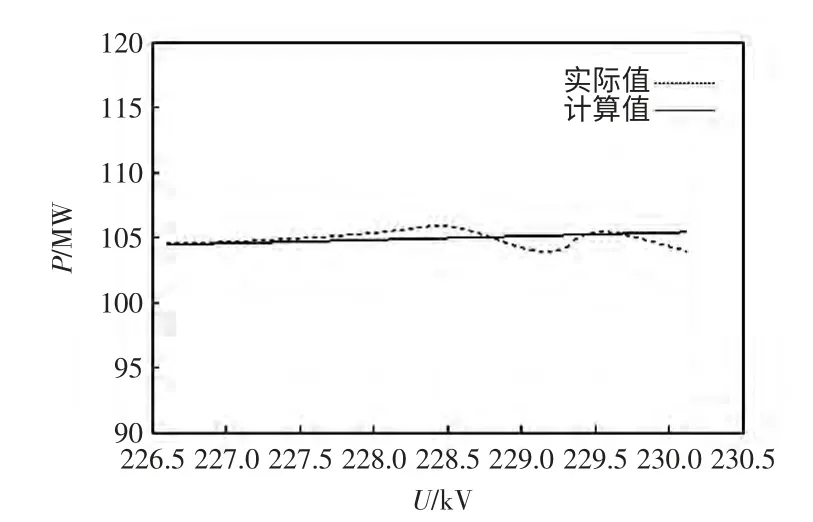
图6 改进遗传K 均值算法的第2 类曲线Fig.6 2nd clustering results of improved genetic and K-means algorithm algorithm

第2 类误差拟合如表5 所示。对比可以看出，在聚类数目为6 时，K 均值和遗传算法的曲线误差较大，对比聚类数目为11 时本文方法，其聚类数目对于负荷特征分类结果精确度的影响大。本文利用可变长编码方案，让聚类数目自动变化，可以获得更好的聚类效果。

表5 第2 类拟合误差比较Tab.5 2nd clustering fitting errors comparison

本文方法确定聚类数目为11 后，采用K 均值和遗传算法，设置初始聚类中心数目为11，并对定长为11 的染色体进行聚类分析，所得结果如表6所示。其中，用定长为11 的染色体编码的遗传算法所得聚类结果和本文方法所得结果一致。

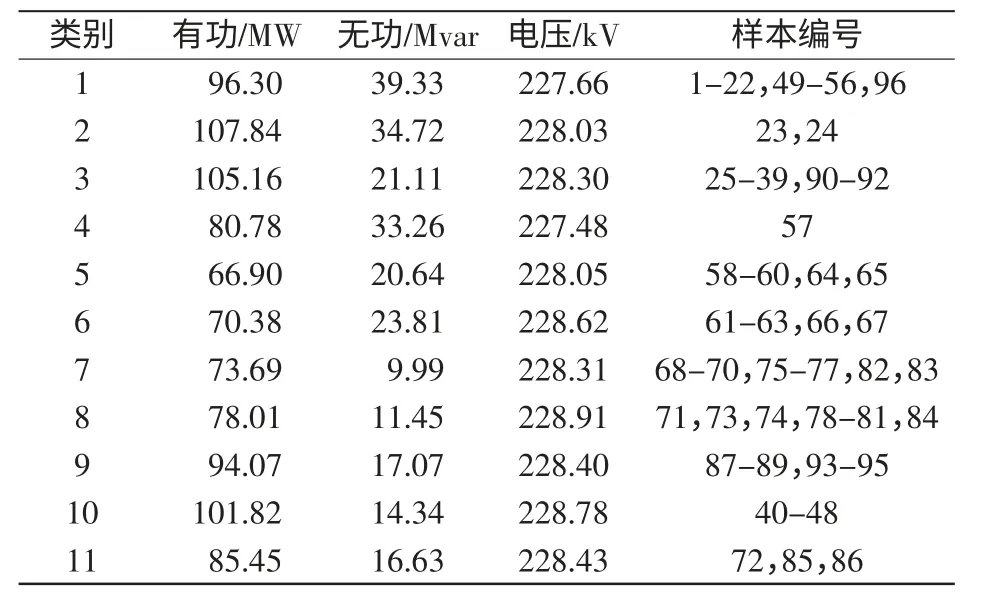
表6 K 均值算法聚类结果Tab.6 K-means algorithm clustering results

选取2 种方法中的第1 类负荷特征进行参数辨识，建立等效模型，并将结果进行比较。第1 类负荷参数辨识结果见表7。

表7 第1 类参数辨识结果Tab.7 Results of 1st parameters identification

聚类数目为11 的情况下，将上述2 算法结果中的有功功率拟合曲线进行比较，如图7 和图8所示。

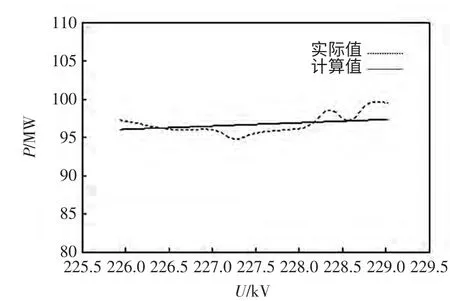
图7 K 均值算法第1 类拟合曲线Fig.7 1st clustering curves of K-means algorithm

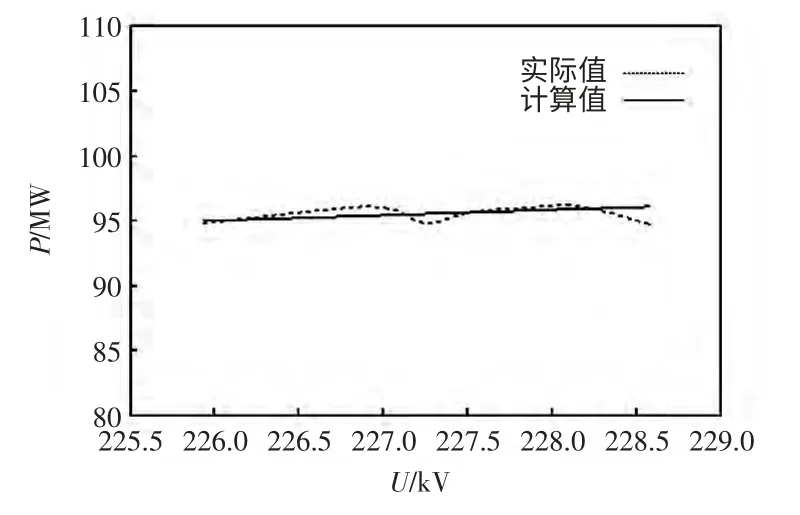
图8 改进遗传K 均值算法第1 类拟合曲线Fig.8 1st clustering curves of improved genetic and K-means algorithm

第1 类K 均值聚类方法和本文方法聚类结果拟合误差如表8 所示。对比可以看出，初始聚类中心的选择会影响最终的分类结果。本文方法利用遗传算法自动搜索最优聚类中心，获得了更好的聚类效果。

表8 第1 类拟合误差比较Tab.8 1st fitting errors comparison

4 结语

负荷特性具有随机性、时变性和多样性的特点，在负荷建模时需要对电力负荷进行分类处理，从而提高建模的准确性。本文提出一种改进遗传算法和K 均值聚类相结合的方法，在利用K 均值聚类的快速全局搜索能力和遗传算法的局部搜索寻优特点的同时，主要针对聚类数目的寻优以及聚类中心的确定，克服其他聚类方法遇到的聚类数目不确定问题，从而提高聚类准确性。实例分析表明，用本文方法对电力综合负荷特性进行分类，相比于其他2 种方法，获得了更为理想的分类效果。

[1]李培强，李欣然，林舜江（Li Peiqiang，Li Xinran，Lin Shunjiang）.电力负荷建模研究述评（Critical review on synthesis load modeling）[J]. 电力系统及其自动化学报（Proceedings of the CSU-EPSA），2008，20（5）：56-64，123.

[2]张红斌，汤涌，张东霞，等（Zhang Hongbin，Tang Yong，Zhang Dongxia，et al）.负荷建模技术的研究现状与未来发展方向（Present situation and prospect of load modeling technique）[J]. 电 网 技 术（Power System Technology），2007，31（4）：6-10.

[3]李培强，李欣然，陈辉华，等（Li Peiqiang，Li Xinran，Chen Huihua，et al）. 基于模糊聚类的电力负荷特性的分类与综合（The characteristic classification and synthesis of power load based on fuzzy clustering）[J]. 中国电机工程学报（Proceedings of the CSEE），2005，25（24）：73-78.

[4]曾博，张建华，丁蓝，等（Zeng Bo，Zhang Jianhua，Ding Lan，et al）.改进自适应模糊C 均值算法在负荷特性分类的应用（An improved adaptive fuzzy C-means algorithm for load characteristic classification）[J]. 电力系统自动化（Automation of Electric Power Systems），2011，35（12）：42-46.

[5]鞠平，金艳，吴峰，等（Ju Ping，Jin Yan，Wu Feng，et al）.综合负荷特性的分类综合方法及其应用（Studies on classification and system of composite dynamic loads）[J].电力系统自动化（Automation of Electric Power Systems），2004，28（1）：64-68.

[6]白雪峰，蒋国栋（Bai Xuefeng，Jiang Guodong）.基于改进K-means 聚类算法的负荷建模及应用（Load modeling based on improved K-means clustering algorithm and its application）[J]. 电力自动化设备（Electric Power Automation Equipment），2010，30（7）：80-83.

[7]张红斌，贺仁睦，刘应梅（Zhang Hongbin，He Renmu，Liu Yingmei）.基于KOHONEN 神经网络的电力系统负荷动特性聚类与综合（The characteristic clustering and synthesis of electric dynamic loads based on Kohonen neural network）[J].中国电机工程学报（Proceedings of the CSEE），2003，23（5）：1-5，43.

[8]廖向旗，李欣然，李培强，等（Liao Xiangqi，Li Xinran，Li Peiqiang，et al）.基于灰色关联度聚类的负荷特性分类（Classification of substation load characteristic based on gray relevancy clustering）[J]. 电力科学与技术学报（Journal of Electric Power Science and Technology），2007，22（2）：28-33.

[9]舒祥波（Shu Xiangbo）.一种自适应遗传算法的聚类分析及应用（Analysis and application of an adaptive genetic algorithm of clustering）[J].信息技术（Information Technology），2011，（4）：190-192，196.

[10]赖玉霞，刘建平，杨国兴（Lai Yuxia，Liu Jianping，Yang Guoxing）.基于遗传算法的K 均值聚类分析（K-means clustering analysis based on genetic algorithm）[J].计算机工程（Computer Engineering），2008，34（20）：200-202.

[11]戴文华，焦翠珍，何婷婷（Dai Wenhua，Jiao Cuizhen，He Tingting）. 基于并行遗传算法的K-means 聚类研究（Research of K-means clustering method based on parallel genetic algorithm）[J]. 计算机科学（Computer Science），2008，35（6）：171-174.