基于BWD 谱峭度的暂态电能质量扰动分类识别

陈 刚，刘志刚，张巧革

（1.西南交通大学电气工程学院，成都610031；2.四川省资阳电力公司，资阳641300）

随着电力系统规模的不断扩大和各种电力电子设备、非线性负荷、冲击性负荷的大量投入，电能质量水平与用户要求之间的差距日益加大，严重影响工业产品质量和居民日常生活，所带来的问题引起各国电力工作者的高度重视，暂态电能质量也逐渐成为供电部门和广大用户所共同关心的问题[1-2]。现有装置对暂态扰动的监测识别存在着十分明显的局限性，监测的指标较少，且大多产品只能针对电压暂降、电压暂升和电压中断这3种扰动进行监测识别，对脉冲暂态、振荡暂态的监测识别比较缺乏。

特征提取是暂态扰动识别的首要步骤，其目的是使不同类别的扰动相互能够得到充分区分，有效减少输入分类器的向量维数，提高分类速度和准确度。目前，常用的特征提取方法有：基于多分辨率得到的信号子频带的能量[3]、小波变换系数的标准差[4]、小波熵[5]、基于S 变换得到的各种特征[6]等。对于扰动信号的特征提取，目前尚未找到一种特别适合的方法，各种新方法的使用也在不断探索中。

峭度是随机变量的四阶累计量，作为一个全局性指标不能反映特定信号分量的变化情况，因此，为了克服峭度在工程应用中的不足之处，文献[7]提出了谱峭度SK（spectral kurtosis）方法，并用来检测信号中的暂态成分；文献[8]定义谱峭度为一个过程偏离高斯分布的程度，并在将其应用到轴承故障诊断中；文献[9]系统定义了谱峭度，提出了基于短时傅里叶变换STFT（short-time Fourier transform）的谱峭度方法，并且在理论上进行了证明，论证了其具有检测加性噪声中非平稳、非高斯信号特征的能力；文献[10]提出了基于Morlet 小波变换WT（wavelet transform）的谱峭度法，通过构造最优Morlet 小波滤波器来诊断回转机械故障；文献[11]提出基于WVD（Wigner-Ville distribution）的谱峭度法，并将其应用到轴承的故障诊断中。

谱峭度能够表征信号中的非平稳和非高斯成分，并且能够自动抑制白噪声干扰。本文提出一种基于巴特沃斯分布BWD（Butterworth distribution）的谱峭度计算新方法，并将其用来提取脉冲暂态和振荡暂态2 类扰动的特征。通过求取2 类暂态扰动信号的谱峭度，提取各自特征向量，输入粒子群PSO（particle swarm optimization）优化参数的支持向量机SVM（support vector machine），对2 类暂态扰动信号进行分类。通过仿真分析验证了本文方法的可行性和有效性。

1 谱峭度的定义

考虑非平稳信号的Wold-Cramer 分解，定义Y（t）为由信号X（t））激励的系统响应[9]，即

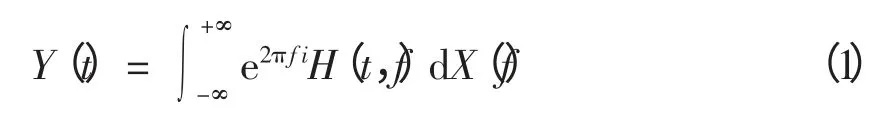
式中，H（t，f）为系统的时变传递函数，是信号Y（t）在频率f 处的复包络。

S2nY（f）为2n 阶瞬时矩，是复包络能量的度量，可定义为

则Y（t）的四阶谱累积量定义为

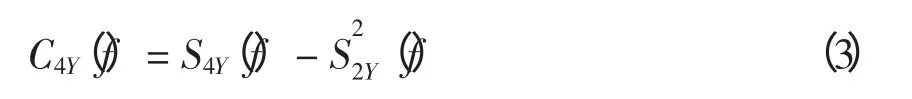
当n 分别取1、2 时，谱峭度可定义为

2 基于BWD 的谱峭度计算方法

现有谱峭度计算方法在理论和实际应用上虽然已经取得了一些成果，但也存在各自的缺陷。如：STFT 谱峭度方法受窗函数的影响较大，一旦窗函数确定，时频分辨率也就确定，时间和频率分辨率只能折中选择，分辨率不高；WT 谱峭度方法在尺度变化上较为固定，且不能显示足够的尺度分辨率来匹配所有可能的瞬态信号成分；WVD 谱峭度方法时频分辨率较高，但是存在交叉项的干扰，导致出现错误的谱峭度成分；BWD 能够保持高的时频分辨率的同时有效抑制交叉项，且满足Kernel类时频分布的大多数时频分布性质。

本文提出一种基于BWD 的谱峭度计算新方法其计算方法的主要步骤如下。

步骤1 计算1 个非平稳随机信号x（t）的Butterworth 分布[12]，结果为

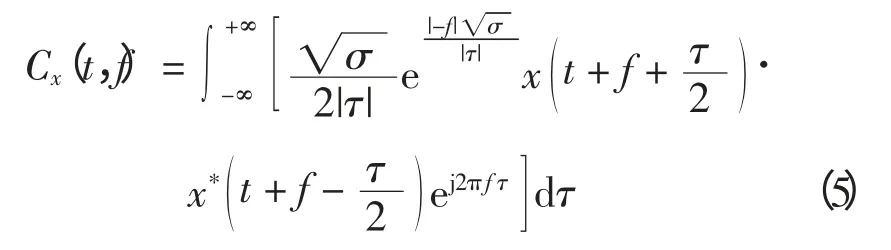
步骤2 根据Butterworth 分布求取x（t）的2阶瞬时谱距S2（f）和4 阶瞬时谱距S4（f），即

式中，〈·〉k为k 阶平均值。

步骤3 根据谱峭度定义，求得谱峭度，即

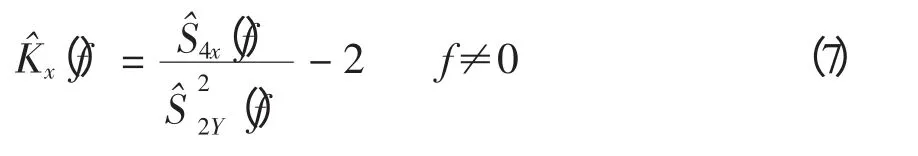
基于BWD 的谱峭度法，继承了BWD 较高的时频聚焦性和抑制交叉项干扰的能力，更清晰、准确地表征信号中包含的非平稳和非高斯成分。

3 基于BWD 谱峭度的暂态扰动分类原理

本文所提出的基于BWD 谱峭度的暂态扰动分类方法的核心思想是：①利用基于BWD 谱峭度方法求取脉冲暂态和振荡暂态扰动信号的谱峭度，将谱峭度的最大值、最小值和均值作为特征量；②采用PSO 优化参数的SVM 作为分类器对2类暂态扰动信号进行分类识别。其具体算法流程如图1 所示。

图1 算法原理框图Fig.1 Diagram of algorithm principle

3.1 基于谱峭度的暂态扰动特征量提取

（1）扰动信号提取。设u（n）为含有扰动信号的输入电压信号，n = 1，2，…，N，N 为数据长度。将u（n）进行小波变换[13]，得

式中：Aj（n）为尺度j 的近似分量；Dj（n）为尺度j 的细节分量；J 为最大分解尺度。当j=J 时，AJ（n）为最大分解尺度下的近似分量，可认为此近似分量只包含工频信号，则扰动信号可表示为

（2）求取扰动信号谱峭度。首先根据式（5）求ur（n）的Butterworth 分布，再根据式（6）得出2 阶和4 阶瞬时谱距，最后根据式（7）获得ur（n）的谱峭度

3.2 SVM 分类识别

支持向量机SVM 是在统计学习理论基础上提出的一类新的机器学习算法，其基于结构风险最小化原理，与传统机器学习方法相比，具有小样本学习能力强、模型推广性能好、高维输入数据处理能力等特性[14]。

（1）核函数的选取。SVM 主要采用的核函数有线性核函数、多项式核函数、径向基核函数和Sigmoid 核函数。线性核函数多用于样本线性可分的情况；其余核函数多用于样本线性不可分的情况，其中径向基核函数用得较为普遍，分类效果也较好[15]。因此，本文选择径向基核函数，表达式为

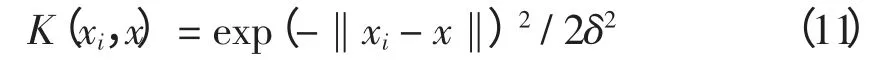
式中，δ 为核宽度。

（2）参数选择。惩罚因子C 和径向基核宽度δ的选取对分类结果有较大影响。本文利用文献[16]中提出的PSO 优化SVM 参数方法，主要步骤为：①读取数据样本，并随机产生（C，δ）作为粒子的初始位置Pi；②计算各粒子适应度函数值，记录最小适应度函数值并更新粒子的位置和速度；③将②中得到的作为模式搜索的初始值，并给定单位向e，精度ε ＞0，置k=0，y=从y出发，依次做平行于e 的轴向探测移动；⑤若，则停止迭代，输出结果；否则返回④。若最大迭代次数|δk|＞ε，则返回②。

（3）训练样本分类。将特征向量和特征向量对应的类别输入PSO 优化参数的SVM 进行训练，然后对测试样本进行分类，得出分类结果。

4 仿真分析

4.1 提取特征量

在实际电网运行中，暂态脉冲主要由雷击、非良好接地、感性负荷投切等原因产生，其中雷击是暂态脉冲的主要成因，对电网的损害也最大。暂态振荡主要由电容投切、电缆、架空线路投入等原因造成[17]。本文利用PSCAD/EMTDC 建立了一个输电线路模型，如图3 所示，其中电源E1、E2 均为220 kV，相角为0；A1、A2、A3 为母线；B1、B2、B3、B4 为断路器；C1、C2、C3 为对地电容。

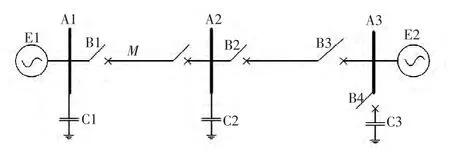
图2 220 kV 输电线路简化模型Fig.2 Simplified model of 220 kV transmission line

（1）产生脉冲暂态。在点M 处加一个控制源为雷电流的受控电流源模拟雷击现象，获得脉冲暂态仿真信号。

（2）产生振荡暂态。在母线A3 处投入1 μF 的接地电容组C3，获得振荡暂态仿真信号。

用PSCAD/EMTDC 产生仿真信号，而实际采集的扰动信号中经常夹杂着噪声，因此加入信噪比SNR（signal to noise ratio）为30 dB 的白噪声模拟实际环境，采样频率设为10 kHz，采样时间设为3 个工频周期，采集的原始含噪脉冲和振荡暂态扰动如图4 所示。利用小波变换分别提取各自扰动分量，如图5 所示。

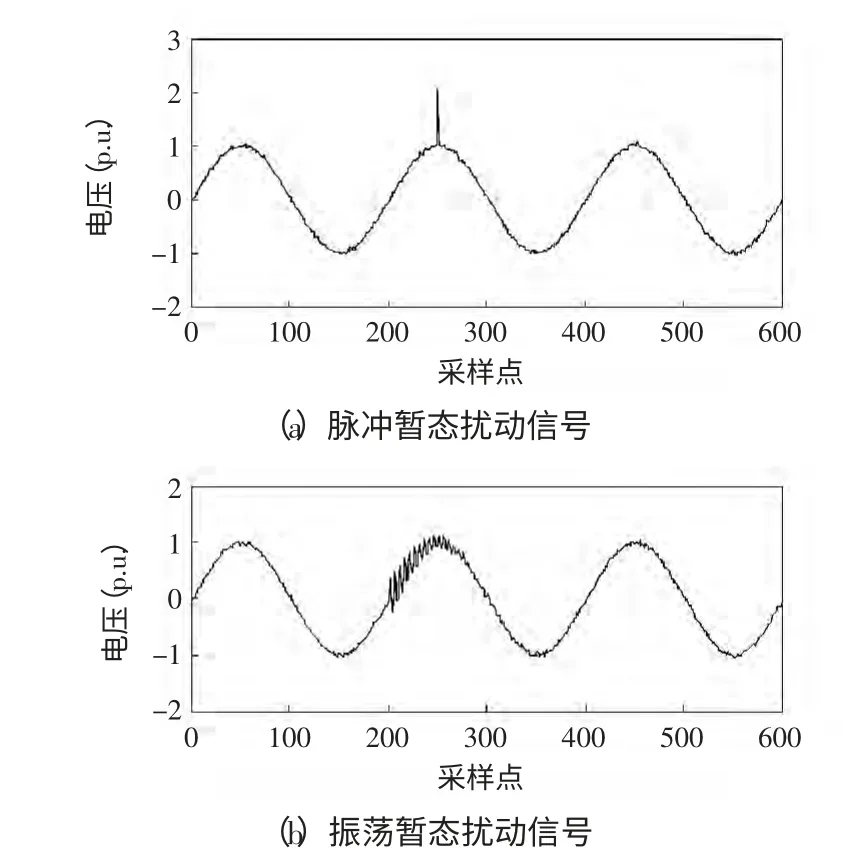
图3 原始含噪扰动信号Fig.3 Original disturbance signals with noise

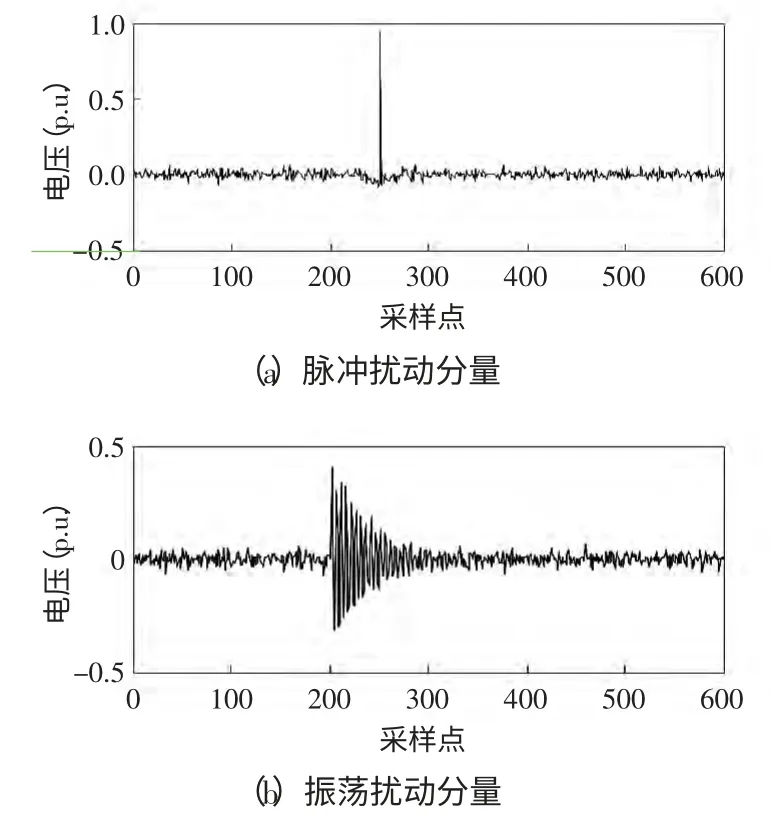
图4 经小波变换提取的扰动分量Fig.4 Extracted disturbance component with wavelet transform

利用第3 节基于BWD 的谱峭度算法，求出含噪脉冲分量和含噪振荡分量的谱峭度，如图6 所示。对原始扰动信号分别加入SNR 为20 dB 和40 dB 的白噪声，得出不同信噪比条件下2 类扰动的特征量，见图6（a）；改变脉冲的幅值、发生的时间，振荡的幅值、持续时间、频率和衰减系数，信噪比选为30 dB，再对2 类扰动分别进行特征提取，见图6（b）。

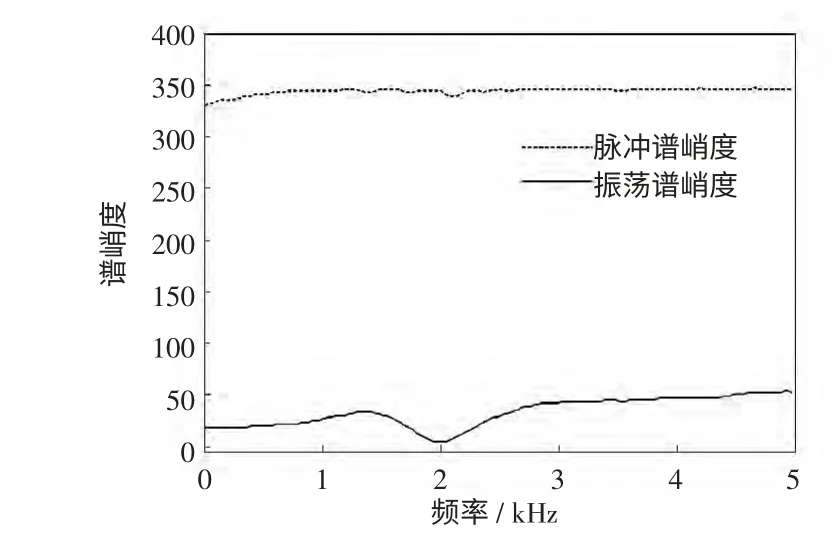
图5 脉冲和振荡扰动谱峭度Fig.5 SpectralKurtosisofpulseandoscillationdisturbance

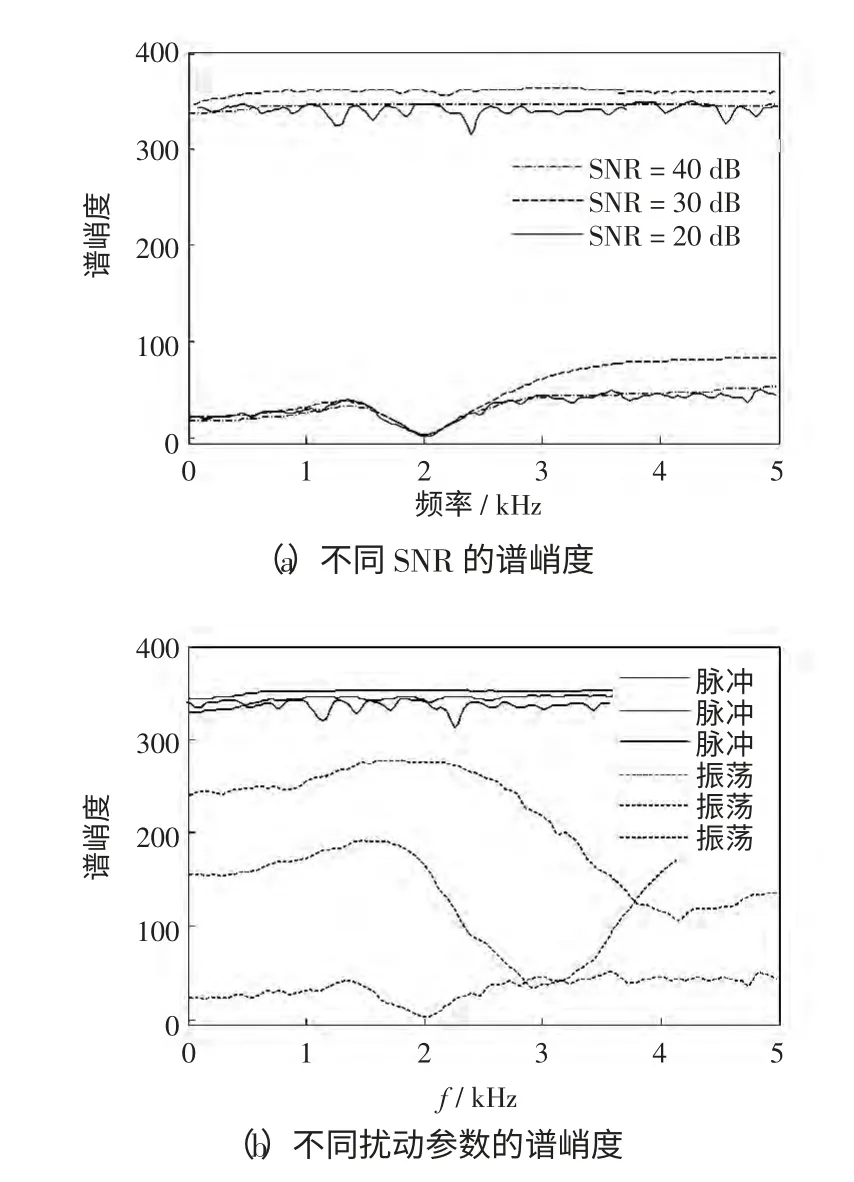
图6 扰动信号谱峭度Fig.6 Spectral kurtosis of disturbance signals

由图6 可见，加入不同SNR（40 dB、30 dB、20 dB）的噪声对谱峭度的计算结果影响不大，对暂态脉冲和暂态振荡提取出的特征量总体趋势基本不变，只是个别值的大小有所不同。当扰动信号参数不同时，可以看出谱峭度对2 类扰动提取的特征比较明显，暂态脉冲特征基本保持不变，但是随着暂态振荡频率的升高，持续时间的缩短，衰减系数的增大，其特征向暂态脉冲靠拢。总体来说，本文提出的基于BWD 谱峭度计算方法对脉冲和振荡2类暂态扰动提取的特征区别明显，有较强的抗噪性能，对后续SVM 分类器的设计与识别非常有利。

4.2 SVM 分类识别

根据第4.1 节2 种暂态扰动产生的模型，再利用PSCAD/EMTDC 软件分别产生2 类扰动信号各250 组仿真数据，采样频率设为10 kHz，采样时间设为3 个工频周期，SNR ≥20 dB。随机选取2 类暂态扰动各50 组作为训练样本，其余各200 组作为测试样本，通过基于BWD 谱峭度方法获得特征向量，将特征向量输入SVM 进行训练和分类。核函数选取为径向基核函数，再利用PSO 对惩罚因子和径向基核宽度进行优化，得到最优参数（C，δ）=（0.45，0.1），分类结果如表1 所示。

由表1 可以得出，对暂态扰动的识别率达到99.5%。脉冲暂态能够完全识别，分错样本均为振荡暂态，通过查验原始振荡样本得出，这些分错振荡样本都是在振荡频率特别高、衰减系数特别大、持续时间特别短的情况下产生，这些条件使得其特征向量更接近于脉冲暂态。PSO 优化参数的SVM 具有较强的小样本学习能力，模型推广能力强，适合于暂态扰动信号的识别。

4.3 叠加其他扰动对分类器的影响

通过叠加其他扰动来讨论SVM 分类器的性能。主要讨论叠加电压暂升、电压暂降、谐波等情况，其产生模型基于文献[18]。采样频率设为10 kHz，采样时间设为3 个工频周期，SNR ≥20 dB。用PSCAD/EMTDC 分别产生叠加了电压暂升、暂降和谐波的脉冲暂态和振荡暂态信号，训练样本各50 组，测试样本各200 组。分类识别结果如表2所示。

由表2 可知，叠加暂升和暂降对SVM 分类器的识别影响不大，因为暂升和暂降只在幅值的大小上变化，其频率保持不变，在提取扰动信号分量时不会对脉冲和振荡造成影响；而谐波的频率范围比较大，可能与脉冲和振荡混叠，影响其识别。总的来说，叠加其他扰动后，本文方法乃有较高识别率。

表1 分类结果Tab.1 Comparison of classification results

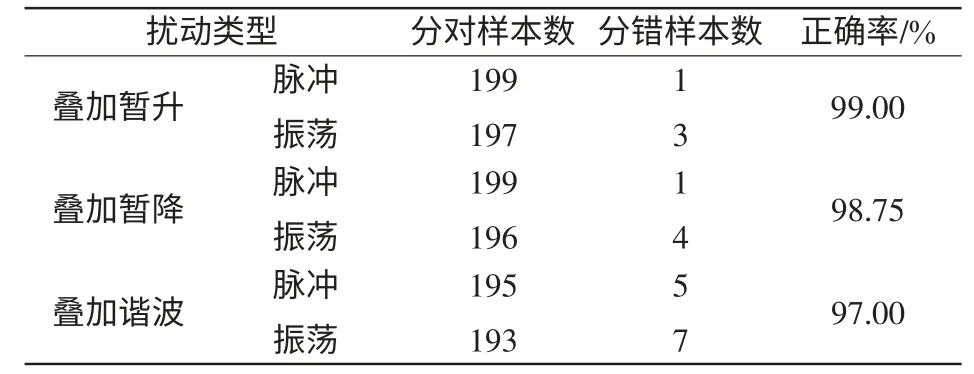
表2 叠加其他扰动的分类结果Tab.2 Classification results with superposing other disturbances

5 结语

BWD 具有较高的时频聚焦能力，同时能够有效抑制交叉项的干扰。根据这一特性，本文提出一种基于BWD 的谱峭度计算新方法，并将其用来提取暂态扰动信号的特征。所提取的特征区分非常明显，且受噪声影响小，对后续分类器的设计很有利。结合PSO 优化参数的SVM 对2 类暂态扰动进行分类，所用训练样本少，识别精度高；且在叠加有电压暂升、暂降和谐波扰动的情况下，仍然能够获得较高的识别率。

[1]Stones J，Collinson A.Power quality[J].Power Engineering Journal，2001，15（2）：58-64.

[2]林海雪（Lin Haixue）.现代电能质量的基本问题（Main problems of modern power quality）[J]. 电网技术（Power System Technology），2001，25（10）：5-12.

[3]刘桂英，粟时平（Liu Guiying，Su Shiping）. 风电接入系统暂态电能质量扰动小波检测方法（Wavelet detection method of transient power quality disturbance for power system connected with wind energy generation）[J].电力系统及其自动化学报（Proceedings of the CSU-EPSA），2011，23（1）：22-27.

[4]张凯，关根志，龙望成，等（Zhang Kai，Guan Genzhi，Long Wangcheng，et al）.基于多分辨率标准差及自组织映射网络的电能质量扰动分类识别（Power quality disturbance classification based on standard deviation of multiresolution analysis and self-organizing feature mapping）[J].电力自动化设备（Electric Power Automation Equipment），2008，28（8）：41-45.

[5]李东敏，刘志刚，蔡军，等（Li Dongmin，Liu Zhigang，Cai Jun，et al）.基于多小波包系数熵和人工神经网络的输电线路故障类型识别方法（Transmission lines fault recognition method based on multi-wavelet packet coefficient entropy and artificial neural network）[J]. 电网技术（Power System Technology），2008，32（24）：65-69.

[6]岳明道（Yue Mingdao）.基于S 变换和分类树的电网暂态电能质量扰动分类辨识（Transient power quality disturbance classification and identification in grid based on S transform and classification trees）[J].电力系统保护与控 制（Power System Protection and Control），2011，39（9）：32-37.

[7]Dwyer R F.Detection of non-Gaussian signals by frequency domain Kurtosis estimation[C]//IEEE International Conference on Acoustics，Speech and Signal Processing，Boston，USA：1983.

[8]Vrabie V D，Granjon P，Serviere C.Spectral kurtosis：from definition to application[EB/OL]. http：//hal.archives-ouvertes.fr/docs/00/06/31/63/PDF/nsip03.pdf，2003.

[9]Antoni J. The spectral Kurtosis：a uueful tool for characterizing non-stationary signals[J].Mechanical Systems and Signal Processing，2006，20（2）：282-307.

[10]Sawalhi N，Randall R B.Spectral Kurtosis optimization for rolling element bearings[C]//Eighth International Symposium on Signal Processing and its Applications. Sydney，Australia：2005.

[11]石锁林，张亚洲，米文鹏（Shi Suolin，Zhang Yazhou，Mi Wenpeng）.基于WVD 的谱峭度法在轴承故障诊断中的应用（Application of Wigner-Ville-distribution-based spectral Kurtosis algorithm to fault diagnosis of rolling bearing）[J]. 振动、测试与诊断（Journal of Vibration，Measurement&Diagnosis），2011，31（1）：27-31，126.

[12]武开有，徐以涛，沈良（Wu Kaiyou，Xu Yitao，Shen Liang）. 基于Butterworth 分布的跳频信号参数估计（Paramer estimation of frequency-hopping signals based on Butterworth distribution）[J].军事通信技术（Journal of Military Communications Technology），2009，30（1）：11-15.

[13]何正友，蔡玉梅，王志兵，等（He Zhengyou，Cai Yumei，Wang Zhibing，et al）.电力暂态信号小波分析的后处理方法研究（A study on post-analysis methods of wavelettransformed power system transient signals）[J].电网技术（Power System Technology），2005，29（21）：46-51.

[14]俞晓冬，周栾爱（Yu Xiaodong，Zhou Luan’ai）.基于改进SVM 模型的电能质量扰动分类（Classification method of power quality disturbances based on improved SVM model）[J]. 电力系统保护与控制（Power System Protection and Control），2010，38（3）：15-19.

[15]张全明，刘会金（Zhang Quanming，Liu Huijin）. 最小二乘支持向量机在电能质量扰动分类中的应用（Application of LS-SVM in classification of power quality disturbances）[J]. 中国电机工程学报（Proceedings of the CSEE），2008，28（1）：106-110.

[16]王喜宾，张小平，王翰虎（Wang Xibin，Zhang Xiaoping，Wang Hanhu）.基于粒子群优化模式搜索的支持向量机参数优化及应用（Parameter optimization of support vector machine and application based on particle swarm optimization mode search）[J]. 计算机应用（Journal of Computer Applications），2011，31（12）：3302-3304，3326.

[17]Abdel-Galil T K，Kamel M，Youssef A M，et al. Power quality disturbance classification using the inductive inference approach[J]. IEEE Trans on Power Delivery，2004，19（4）：1812-1818.