基于分段积温效应的夏季负荷组合预测方法

2014-03-02谭风雷苗振林

电力需求侧管理 2014年2期

谭风雷，苗振林

（东南大学电气工程学院，南京 210096）

电力负荷预测是电力系统规划和运行的基础。电力负荷预测方法一般分为传统预测方法和现代预测方法。电力负荷预测精度受到很多因素的影响，例如：气象因素、经济水平和社会因素等，综合考虑各种因素是提高负荷预测精度的有效途径。

随着经济水平的发展，社会文化的进步，人民生活水平的提高，使得电力负荷不断提高，大功率、高耗能电器的使用越来越普及，降温取暖负荷所占比例越来越大，这使得气象因素对电力负荷的影响越来越显著，尤其是在炎热的夏季。因此，本文将重点研究夏季负荷。

本文主要研究考虑积温效应的温度修正方法。电力负荷的积温效应一般是指在持续低温或高温天气状况下，负荷出现不同程度的反常增长。但实际上，由于负荷的连续性，当2天之间温差较大，负荷相差并不大，这样就会使得相同温度在不同时期，负荷相差较大，本文也将其称为积温效应。文献[1]只是研究了一般的积温效应，没有考虑第二种积温效应。文献[2]分析了积温效应的2种表现形式，但只是对温度进行了分段修正，没有将2种形式分开研究。文献[3]研究了多日积温效应，但是没有研究积温效应持续时间长度对负荷的影响，须将积温效应按持续时间长度分段讨论。

本文主要采用组合方法预测负荷。充分考虑传统负荷预测方法和现代负荷预测方法的优缺点，采用基于多元线性回归法、BP神经网络和支持向量机（SVM）的组合预测方法。文献[4]采用模拟退火法优化BP神经网络，文献[5]采用模拟退火法优化支持向量机（SVM），但是没有给出模拟退火法初值的选择方法。本文采用基于最小二乘法优化的模拟退火法优化参数，既能提高运行效率，又可以得到全局最优解。

在此背景下，本文提出了3种考虑积温效应的温度修正方法预测负荷。首先，分析积温效应的2种表现形式；然后根据积温效应的特点，建立考虑积温效应的温度修正模型；最后利用江苏某地区的工作日负荷作为历史数据，采用基于最小二乘法优化的模拟退火法确定积温效应的最优参数，预测10个工作日的负荷，得到了比较准确的预测结果。

1 积温效应

随着大功率、高耗能电器越来越普及，降温取暖负荷所占比例越来越大，使得气象因素对电力负荷的影响越来越显著,积温效应作为反应阶段性天气状况的负荷,在负荷中占据了越来越高的比例,因此，考虑积温效应的负荷预测变得尤其重要。

1.1 积温效应分析

电力负荷中的积温效应一般是指在持续低温或高温天气状况下，负荷出现不同程度的反常增长，具体的表现形式如下。

（1）持续多天低温或高温天气状况下，负荷会出现不同程度的反常增长。

（2）由于负荷的连续性原理，当2天之间温差较大，但负荷相差不大，这样就会导致相同温度在不同时期，负荷相差较大。

1.2 积温效应量化

根据积温效应的表现形式，本文将积温效应分为多日积温效应和两日积温效应。多日积温效应就是通常意义上的积温效应，两日积温效应就是表现形式（2）。综合考虑积温效应的表现形式，本文提出了一种考虑积温效应的温度修正方法，并将其称为方法一。

式中：Ti、ti分别为第i个预测日的修正温度和实际温度，c1、c2分别为考虑两日积温效应和多日积温效应的气温修正系数，s为积温效应持续时间；针对两日积温效应，修正温度之前需要确定2天之间的温差m；针对多日积温效应，修正温度之前需要确定持续天数n，温度下限TL。

实际上，表达式（1）没有考虑积温效应持续时间长度对负荷的影响，显然持续时间长度不同对负荷影响很大，因此，需要对持续时间分段讨论，本文将其称为分段积温效应，并提出了2种基于分段积温效应的温度修正方法。

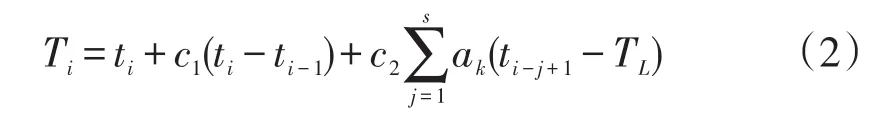
式中：ak（k=1,2,3,4）为分段积温效应系数，当s=n时，k=1；当s=n+1时，k=2；当s=n+2时，k=3；当s≥n+3时，k=4。

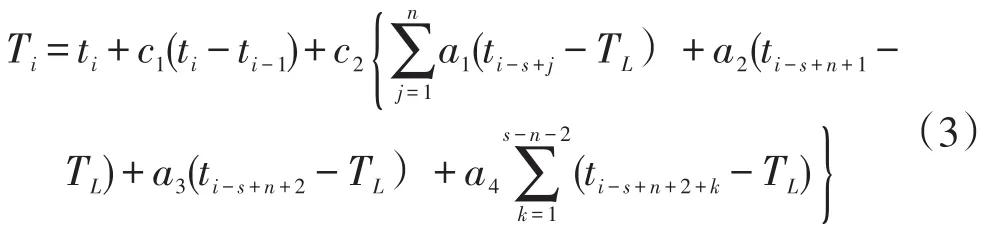
其中，表达式（2）称为方法二，表达式（3）称为方法三。

1.3 积温效应参数确定

根据积温效应的特点和表现形式，本文提出一种具体有效的积温效应参数确定方法。

积温效应参数确定方法的具体步骤。

（1）分别研究日最大温度，日平均温度，日最大负荷对应温度与日最大负荷的相关性，选择与日最大负荷相关性最大的温度作为温度的研究对象。

式中：r为温度与负荷的相关性，ti为第i个预测日的实际温度，-t为平均温度，Pi为第i个预测日的实际负荷，为平均负荷。

（2）建立温度与日最大负荷的一元线性回归模型预测负荷。

式中：Pi(ti)为第i个预测日所对应的预测负荷，a、b分别为回归系数。

（3）将温度修正公式代入式（5）预测第i日负荷，并结合式（6），采用基于最小二乘法优化的模拟退火法（LS-SA）求解最优参数（c1,c2,a1,a2,a3,a4）。

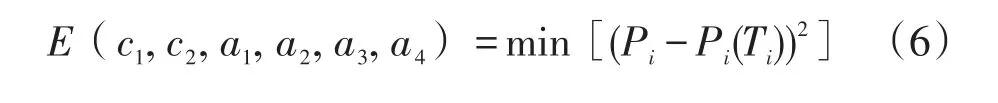
式中：E（c1,c2,a1,a2,a3,a4）为最优参数（c1,c2,a1,a2,a3,a4）所对应的误差平方和。

2 组合预测及参数优化

2.1 组合预测

组合预测（CF）方法是对同一个问题采用2种以上不同预测方法的预测。组合预测模型可能得到一个较好的预测值，在一定程度上优化预测结果。目前，负荷预测方法有很多，主要分为传统预测方法和现代预测方法。传统预测方法包括：灰色系统理论、指数平滑法、时间序列法、回归分析法、卡尔曼滤波法和负荷求导法。传统预测方法主要借助数学工具对负荷进行预测，方法简单，但误差相对较大。现代预测方法包括：相似日法、专家系统法、人工神经网络、小波分析法、模糊理论预测法、支持向量机法。现代预测方法主要借助人工智能进行负荷预测，方法比较复杂，但是误差相对较小，可以很好地满足实际负荷预测要求。充分考虑各种预测方法的优缺点，并结合实际情况，本文选择多元线性回归法（MIR），BP神经网络[12]和支持向量机（SVM）[13—14]这3种预测方法组合预测负荷。

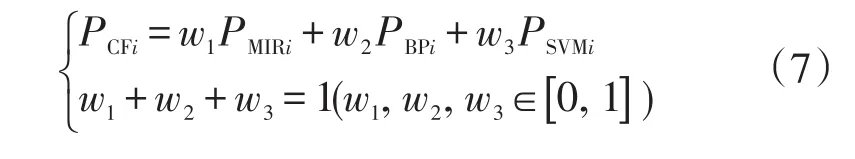
式中：w1，w2，w3为组合系数，PCFi为组合方法预测负荷；PMIRi为回归法预测负荷，具体实现是：借助历史数据，将修正之后的温度值与负荷值进行一元线性回归，得到表达式（5）的参数，再将待预测日修正之后的温度值代入表达式（5）即可预测当日负荷；PBPi为BP神经网络预测负荷，具体实现分为：训练和预测2个部分，首先BP神经网络采用单输入单输出结构，将修正之后的温度值作为输入，负荷值作为输出，借助历史数据多次训练BP神经网络，然后将待预测日修正之后的温度代入训练好的BP神经网络中，即可预测当日负荷；PSVMi为支持向量机（SVM）预测负荷，具体实现是：首先借助历史数据，将修正之后的温度列向量作为训练样本的输入特征，将负荷列向量作为训练样本的输出特征，选择合适的核函数及其相关参数训练支持向量机（SVM），训练之后将待预测日修正之后的温度代入训练好的支持向量机（SVM）中，即可预测当日负荷。

2.2 参数优化

针对积温效应参数和组合预测系数，本文采用基于最小二乘法优化的模拟退火法（LS-SA）确定。传统的模拟退火法（SA）优化参数时，由于初始值很难确定，只能通过经验选取，使得优化结果时常会收敛到局部最优，很难得到全局最优，这在一定程度上影响了模拟退火法的运用推广。而采用最小二乘法优化的模拟退火法，由于采用了最小二乘法，不仅可以降低模拟退火法的迭代时间，提高运行效率，还能够得到全局最优参数。其具体实现步骤：首先，确定系统的目标函数；然后采用最小二乘法多次寻优，找到目标函数最优参数的大致位置；最后将最优参数的大致位置作为模拟退火法的初值代入模拟退火法迭代寻优，得到全局最优参数。

模拟退火算法（SA）[4—5]是一种通用概率演算法，用来在一个大的搜寻空间内找寻命题的最优解。模拟退火是Kirkpatrick等在1983年发明的，它借鉴了物理上金属退火的原理，即将热力学的理论运用到统计学上，其出发点是基于物理中固体物质的退火过程。模拟退火算法从某一较高初始温度出发，伴随温度参数的不断下降，结合概率突跳特性在解空间中随机寻找目标函数的全局最优解，即局部最优解能概率性地跳出并最终趋于全局最优。模拟退火算法是一种通用的优化算法，理论上算法具有概率的全局优化性能。

3 算例分析

由于日最大负荷不仅受温度影响，还受其他一些因素影响，如：节假日和星期类型。因此，本文在分析数据时，首先剔除掉节假日和双休日当天的数据，将正常工作日的数据作为主要的研究对象。本文以江苏某地区2012年6月、7月40组工作日负荷数据作为历史数据，预测8月前10个工作日的负荷。

3.1 参数确定

对大量负荷数据进行分析处理，并结合实际情况，选择最优积温效应参数如表1所示。

表1 积温效应参数

结合积温效应参数确定方法的步骤（3），将江苏某地区2012年6月、7月40组工作日负荷温度数据作为研究对象，代入表达式（5）中，采用最小二乘法优化的模拟退火法（LS-SA）优化得到全局最优参数，如表2、表3所示。

表2 温度修正参数一

表3 温度修正参数二

3.2 结果分析

（1）积温效应结果分析

为了验证所提出的考虑积温效应的负荷预测方法的正确性，将未经修正的温度直接代入回归模型（MIR）进行预测，同时与采用本文温度修正方法进行预测的结果进行对比分析，结果如表4所示。

分析表4可知：①温度修正方法使得负荷预测精度得到很大提高；②温度修正方法三预测效果最好，预测精度达到97.86%，最大相对误差为4.86%，而最小相对误差为0.34%。因此，下文对积温效应研究时，主要采用温度修正方法三。

表4 考虑积温效应的负荷预测结果

为了直观的比较预测结果，绘制了考虑积温效应的负荷预测结果图，如图1所示，横坐标表示8月前10个工作日，纵坐标表示所对应的负荷。

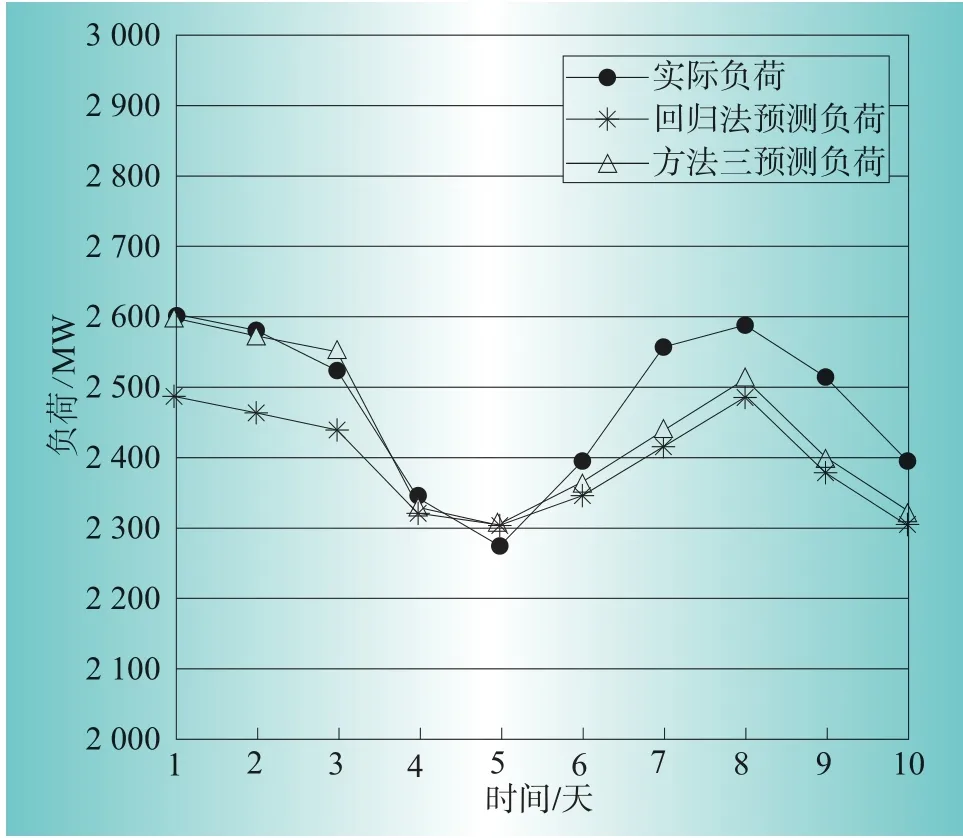
图1 积温效应负荷预测结果

（2）组合预测结果分析

为了减少预测负荷的误差，改进预测效果，本文采用组合预测方法提高预测精度，借助基于最小二乘法优化的模拟退火法优化组合预测系数。首先，分别计算回归法（MIR）预测值、BP神经网络预测值和支持向量机（SVM）预测值；然后将3类预测值代入表达式（7）中，得到关于组合系数w1，w2和w3的组合预测值；接着求解组合预测值相对实际负荷值的相对误差的绝对值；最后，将该值作为基于最小二乘法优化的模拟退火法的目标值，并结合表达式（7）中的限制条件，即可求解组合预测系数，求解结果如表5所示，将得到的组合预测系数代入组合预测模型，借助修正之后的温度值即可预测负荷，预测结果如表6所示。

分析表6可知：①组合预测（CF）方法负荷预测效果好，预测精度达到98.42%，而最大相对误差为4.17%，最小相对误差为0.14%，可以满足系统调度人员的需要；②尽管组合预测（CF）平均相对误差大于支持向量机（SVM），但是最大相对误差小于SVM，误差平方和远小于SVM，从统计学原理上讲，预测误差波动更小，预测效果更加稳定；③负荷预测方法选择应该从2个方面考虑：平均相对误差和误差平方和。平均相对误差研究整体负荷预测精度；误差平方和研究预测误差波动程度。负荷预测时应该充分考虑这2点，结合多目标规划问题选择负荷预测方法。

表5 组合预测系数

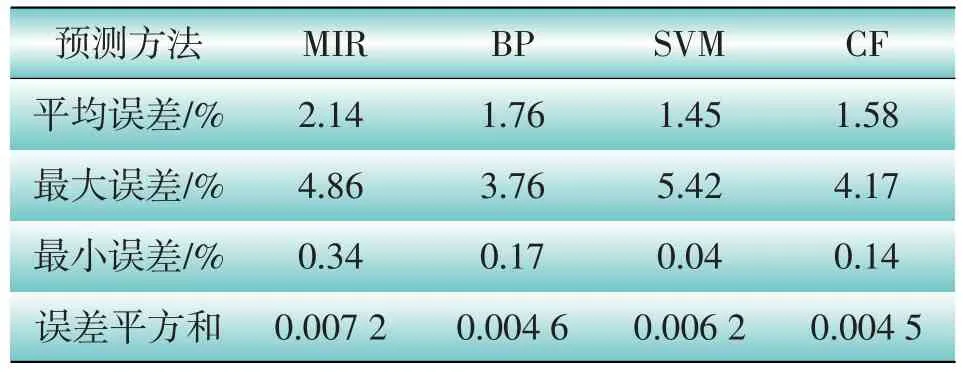
表6 组合预测结果

为了直观的比较预测结果，绘制了组合预测结果图，如图2所示，横坐标表示8月前10个工作日，纵坐标表示所对应的负荷。

图2 组合预测结果

4 结论

气象因素对夏季负荷有着很大的影响，尤其是温度及其积温效应。

本文分析了积温效应的2种表现形式：多日积温效应和两日积温效应。结合其表现形式，提出了3种考虑积温效应的温度修正方法，并进行了分析比较。以江苏某地区2012年6月、7月的负荷数据作为历史数据，采用基于最小二乘法优化的模拟退火法（LS-SA）求解积温效应的相关参数，并对8月前10个工作日的负荷进行预测，最后采用基于多元线性回归法、BP神经网络和支持向量机（SVM）的组合预测方法预测负荷，结果表明：所提出的基于分段考虑积温效应的夏季负荷预测方法预测精度高，可以满足系统调度人员的需要，能够得到很好的运用。

[1]蒋建东，程志豪，朱明嘉.考虑积温效应的短期负荷组合预测方法[J].电力自动化设备，2013,31（10）：28-31.

[2]李嘉龙，李小燕，刘思捷，等.考虑气温累积效应的短期负荷预测[J].华北电力大学学报，2013,40（1）：49-53.

[3]肖伟，罗滇生，董雪.积温效应分析及日最大负荷预测中的应用[J].微计算机信息，2009,25（11）：262-264.

[4]张林，刘先珊，阴和俊.基于模拟退火的Gauss-Newton算法神经网络在短期负荷预测中的应用[J].武汉大学学报，2005,38（4）：28-33.

[5]李瑾，刘金朋，王建军.采用支持向量机和模拟退火算法的中长期负荷预测方法[J].中国电机工程学报，2011,31（16）：63-66.

[6]王鹏，邰能灵，王波，等.针对气象因素的短期负荷预测修正方法[J].电力系统自动化，2008,32（13）：92-96.

[7]王治华，李扬，赵翠宇，等.南京市夏季气温敏感负荷研究[J].电力系统自动化，2002,26（3）：60-63.

[8]金丽莉，谭风雷，吴志坚，等.考虑积温效应的负荷预测研究[J].电力需求侧管理，2013,15（1）：7-10.

[9]胡长洪.考虑实时气象因素的短期负荷预测[D].杭州：浙江大学，2010.

[10]黄永高.电力负荷预测方法的研究[D].南京：东南大学，2010.

[11]李元诚，方廷健，于尔铿.短期负荷预测的支持向量机方法研究[J].中国电机工程学报，2003,23（6）：55-59.

[12]张少迪.基于PSO-BP神经网络的短期负荷预测算法[J].现代电子技术，2013,36（12）：155-158.