一种改进的共轭梯度法的全局收敛性
2014-03-02蒙诗德陈献媛邱小芬区红蓝
□蒙诗德,陈献媛,邱小芬,区红蓝
(1,2,3,4.玉林师范学院 数学与信息科学学院,广西 玉林 537000)
一种改进的共轭梯度法的全局收敛性
□蒙诗德1,陈献媛2,邱小芬3,区红蓝4
(1,2,3,4.玉林师范学院 数学与信息科学学院,广西 玉林 537000)
本文给出了一种新的共轭梯度公式该公式在标准Wolfe线搜索下具有充分下降性和全局收敛性.
无约束优化;共轭梯度法;线搜索;全局收敛性
1 引言
考虑无约束优化问题

其中f∶Rn→R为一阶连续可微的非线性函数,其梯度函数记为g=g(x).
求解无约束优化问题(1.1)的一般方法有如下迭代公式

其中αk为搜索步长,一般采用某个线搜索来获得,常用的线搜索有精确线搜索和非精确线搜索, 典型的非精确线搜索有wolfe非精确线搜索, 简称wolfe线搜索. 其中标准wolfe线搜索要求αk满足
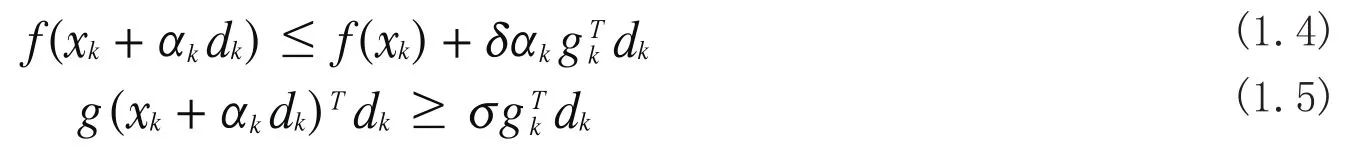
其中δ和σ是满足0<δ<σ<1的常数.
强wolfe线搜索要求αk满足(1.4)和

推广的wolfe线搜索要求满足(1.4)和

其中σ1∈(δ,1),σ1≥0.βk是标量,不同的βk对应不同的共轭梯度法,文献[1-7]已给出选取βk的几种公式,各种公式的全局收敛性一直被许多学者所关注. 其中Powell[8]证明了FR 方法在精确线搜索下具有全局收敛性;Al-Baali[9]在非精确线搜索搜索下证明了FR方法具有全局收敛性但数值结果较差;文献[7]提出了βk的一种计算公式
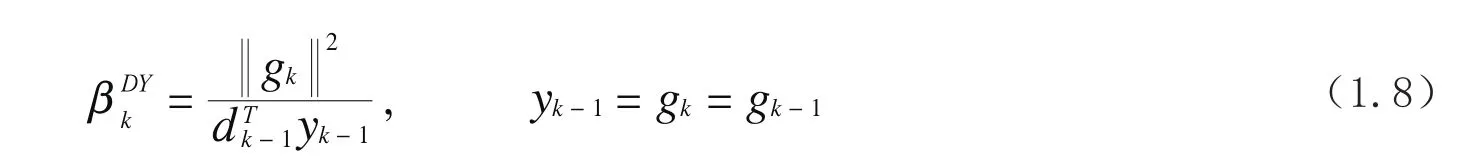
相应得到共轭梯度法,并证明了在标准wolfe搜索下的全局收敛性;文献[10]提出了新的DY-型共轭梯度公式:

并证明了在推广wolfe线搜索下的全局收敛性;文献[11]提出了新的共轭梯度公式:
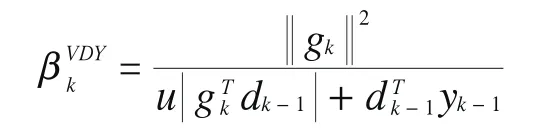
其中u>1,并证明了在标准wolfe线搜索下的全局收敛性. 本文吸收文献[10-11]的思想,提出一个新的βk公式,并证明新公式在标准wolfe线搜索下具有充分下降性和全局收敛性.
2 新的共轭梯度公式及其下降性
2.1 新的共轭梯度公式和算法:
本文给出新的共轭梯度公式:

其中rk满足(1.9),u>1.
算法A:
Step1 任意给定x1∈Rn,令d1=-g1,k∶=1,若g1=0,则停止;
Step2 计算αk>0,满足式(1.4),(1.5);
Step3 令xk+1=xk+αkdk,计算gk+1=g(xk+1),若gk+1=0,则停止;
Step4 由(1.3)式计算dk+1,其中βk满足(1.9)式和(2.1)式,置k∶=k+1,转Step2.
2.2 新公式的下降性
为了以后证明需要,提出两个基本假设:
(H1)f在水平集Ω={x∈Rn|f(x)≤f(x1)}上有下界,其中x1为初始点;
(H2)f在水平集Ω连续可微,其梯度向量g满足Lipschitz条件,即存在常数L>0,使得
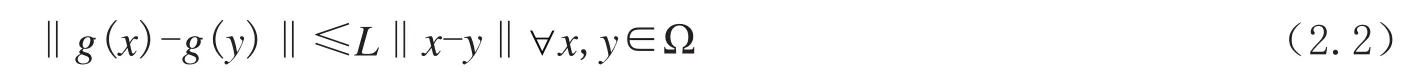
定理2.1若假设(H1),假设(H2)成立,βk满足(1.9)式和(2.1)式,αk由线搜索(1.4)式和(1.5)式所确定. 则对∀k≥1,有

即新算法A具有充分下降性.
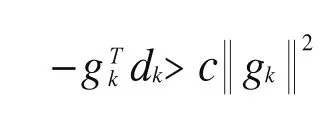
3 新算法的全局收敛性
先给出一个引理.
引理3.1若假设(H1),假设(H2)成立,对于(1.2)式和(1.3)式,βk满足(1.9)式和(2.1)式,αk由线搜索(1.4)式和(1.5)式所确定. 则Zoutendijk成立,即

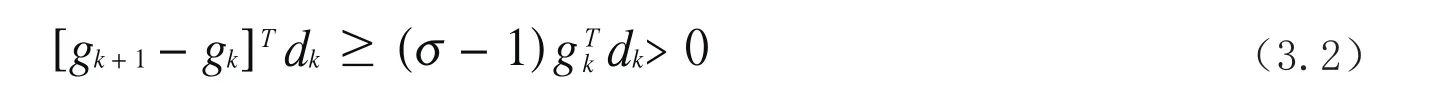
另一方面,由Lipschitzts 条件(2.2)式有

由(3.2)式和(3.3)式得

由(1.4)式得

上式两边求和得
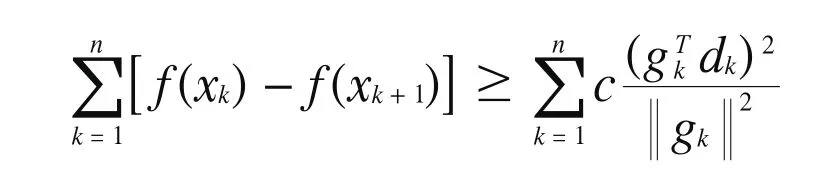
由于{f(xk)}为收敛数列,上式令n→∞两边取极限知
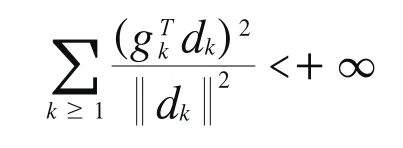
因此,Zoutendijk条件成立,引理3.1得证.
定理3.1若假设(H1),假设(H2)成立,对于(1.2)式和(1.3)式,βk满足(1.9)式和(2.1)式,αk由线搜索(1.4)式和(1.5)式所确定. 则算法或者终止于稳定点或者

证明:若定理不成立,则存在γ>0,使得

由(1.9)式知

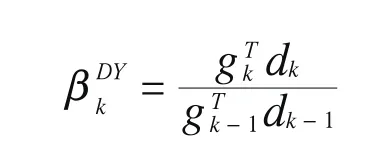
将(1.3)写成dk+gk=βkdk-1两边取模平方并由(3.6)式得上式两边除以得
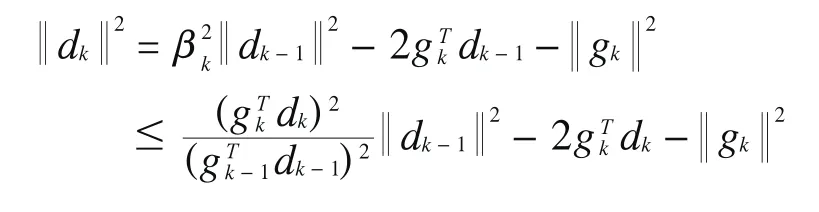

这与Zoutendijk条件矛盾. 故定理得证. ■
[1]Hestenesand M R, Stiefel E L. Methods of conjugate gradient for solving linear systems[J]. J Res Nat Bur Standards Sect, 1952, 49: 409-436.
[2]Fletcher R, Reeves C. Function minimization by conjugate gradients[J].Compute J, 1964, 7: 149-154.
[3]Polak E, Ribiere G.. Note sur la convergence de directions conjugees[J]. Rev Francaise Informat Recherche Operationelle, 3e Année, 1969, 16: 35-43.
[4]Polak B T. The conjugate gradient method in extremem problems [J]. USSR Comp Math and Math Phys, 1969, 9: 94-112.
[5]Fletcher R. Practical Methods of Optimization, vol 1: Unconstrained Optimization[M]. 2nd edition. New York: Wiley, 1987.
[6]Liu Y ,Storey C. Efficient Generalized Conjugate Gradient Algorithms, part 1: theory [J]. Journal of Optimization Theory and Application, 1991, 69: 129-137.
[7]Dai Y H, Yuan Y. A Nonlinear Conjugate Gradient with a Strong Global Convergence Property[J]. SIAM Journal of Optimization,2000,10:177-182.
[8]Powell M J D. Nonconvex minimization calculations and the conjugate gradient method, in: Lecture Notes in Mathematics vol J [M ]. Berlin: Springer-Verlag, 1984:122-141.
[9]M Al-Baali. Descent property and global convergence of the Fletcher-Reeves method with inexact line search [J]. IMA J. Numer Anal, 1985, 5: 121-124.
[10]蒙诗德,刘利英,吴庆军等. 一类新的DY-型共轭梯度法的全局收敛性[J].广西科学,2006,13(4):276-278.
[11]刘金魁,王开荣.一种改进的共轭梯度法及全局收敛性[J].经济数学,2008,25(3):309-35.
[12]戴或红,袁亚湘. 非线性共轭梯度法[M].上海:上海科学出版社,2000,69.
【责任编辑 谢明俊】
The Global Convergence Property Of An Improved Conjugate Gradient Method
MENG Shi-de1,CHEN Xian-yuan2,QIU Xiao-fen3,OU Hong-lan4
(1, 2, 3, 4. College of Mathematics & Information Science, Yulin Normal University, Yulin, Guangxi, 537000)
This paper provides a new formula of Conjugate Gradientand this formula has abundant descendent property and Global Convergence Property under the standard of Wolfe linear search.
unconstrained optimization, conjugates gradient method, line search, global convergence
O224
A
1004-4671(2014)05-0017-04
2014-09-08
2014年玉林师范学院大学生创新创业训练计划项目(编号:122)。
蒙诗德(1956~),男,广西北流人,玉林师范学院数学与信息科学学院副教授,研究方向:优化理论。
