双层Lengyel-Epstein模型不同耦合形式下的图灵斑图
2014-03-01白占国景宏华李新政李新娟
白占国,景宏华,李新政,李 燕,李新娟
(1.河北科技大学理学院,河北石家庄 050018;2.河北师范大学河北省职业技术教育研究所,河北石家庄 050080)
双层Lengyel-Epstein模型不同耦合形式下的图灵斑图
白占国1,景宏华2,李新政1,李 燕1,李新娟1
(1.河北科技大学理学院,河北石家庄 050018;2.河北师范大学河北省职业技术教育研究所,河北石家庄 050080)
采用双层Lengyel-Epstein模型研究了2个子系统在不同耦合形式下斑图的形成机制。研究3种不同波数比的条件下,耦合形式和耦合强度对斑图的形成的重要作用。当波数比为1时,2个子系统会出现相同的简单斑图(如简单六边形、四边形和条纹斑图),耦合形式和耦合系数的改变未对斑图的形成产生影响;当波数比大于1时,短波系统出现种类丰富的复杂斑图。由于图灵模间发生共振耦合:线性耦合系统出现白眼超六边和类蜂窝斑图,非线性耦合系统选择环状超六边和白眼等复杂超点阵斑图。另外,2种耦合形式图灵模产生共振所需的耦合强度不同。
Lengyel-Epstein模型;图灵模;耦合;斑图
白占国,景宏华,李新政,等.双层Lengyel-Epstein模型不同耦合形式下的图灵斑图[J].河北科技大学学报,2014,35(2):134-138.
BAI Zhanguo,JING Honghua,LI Xinzheng,et al.Analysis of Turing pattern in two-layer coupled Lengyel-Epstein model[J].Journal of Hebei University of Science and Technology,2014,35(2):134-138.
斑图是自然界广泛存在的一种在时空上具有某种规律性的非均匀结构,是均匀恒定状态的线性失稳导致了系统某种时空对称性破缺的结果[1-5]。人们按斑图包含空间波矢的多少,将斑图粗略地分为3类:1)具有单个波矢的简单斑图,2)包含2个或2个以上空间波矢的复杂斑图,3)具有无限个波矢的混沌态,经空间分析发现复杂斑图是由简单子斑图结构按照一定的波长关系组合而成。由于复杂斑图的组成单元是一个介观结构,既具有“准粒子”的微观特性,又具有整体相关的宏观特征,所以超点阵复杂斑图已成为研究的热点。
近年来,人们利用多种形式在实验和理论上获得了种类丰富的超点阵斑图[6-9],其中以介质阻挡放电系统最为显著,在该系统中已获得了蜂窝、白眼、超四边、超六边、点线斑图和螺旋波等复杂斑图[10-12]。人们根据BARRIO等提出超点阵斑图的形成是由于2个模相互作用的观点[13],开始利用双层耦合模型对实验中观察到的超点阵斑图进行理论模拟,并获得了许多有意义的研究成果[14-16]。已有文献主要利用模与模的线性耦合作用获得超点阵斑图,对非线性相互作用研究较少。在本研究中,采用双层Lengyel-Epstein数值模型,通过改变2个图灵模的波数比和耦合强度,从模与模的线性和非线性耦合2个方面,获得了种类丰富的斑图,分析了图灵模对不同斑图形成的影响,并从理论上分析了复杂图形的形成机理及其动力学行为。
1 模 型
图灵在1952年首先利用化学反应扩散方程组对斑图的形成进行了理论解释[17],目前用于研究图灵分岔斑图的主要有Schnackenberg、Brusselator和 Lengyel-Epstein 等模型[18-20]。本研究所采用的模型是CIMA化学反应系统双层耦合的Lengyel-Epstein方程,每层包括一个活化子和一个禁阻子,在无量纲的情况下该模型形式如下:

其中i和j表示2个子系统1(u1,v1)和2(u2,v2),u和v分别为活化子和禁阻子的浓度;Du和Dv分别为u和v变量的扩散系数,α,β为2个子系统耦合强度,动力学行为由控制参数a和b所决定。在本文中固定a=15和b=9。该系统具有唯一的均匀定态解,对该均匀定态解作线性稳定性分析可得到斑图动力学中最常见的2类初级分岔现象:当控制参数b满足时,系统经历霍普夫分岔;当b满足时,系统经历图灵分岔,并产生一组特征波数均为的图灵模,从式中可以看出图灵模的波数kc反比于2个变量扩散系数Du和Dv的乘积。图1是2个系统的色散关系:具有较大扩散系数的失稳模q(长波模)具有较小的波数,而具有较小扩散系数的稳定模kc(短波模)具有较大的波数。
数值模拟采用欧拉向前差分的方法进行积分,在一个含有N×N(128×128)个格子的二维平面上进行,时间积分步长为Δt=0.01个时间单位,初始条件为均匀定态上加一个很小的随机扰动,边界条件选用周期性边界条件。

图1 2个耦合系统色散关系Fig.1 Dispersion relation of two coupled mode
2 结果与分析
由于双层模拟系统中斑图的选择完全取决于2个图灵模之间的地位与相互作用,因此通过合理选择参数使2个子系统分别具有长波模和短波模,保持长波模为失稳形式、短波模为线性稳定形式,进而讨论两模作用引起的复杂斑图。
图2中是波数比为1时,不同情况下2个子系统出现的简单六边形斑图。从图2中可以看出:无论耦合系数和形式如何改变,两子系统形成斑图都与子系统无耦合时生成的简单六边形相同,均具有相同的空间点阵形式,说明两子系统波数相等时斑图不受耦合项的影响,仅与扩散系数有关,且随扩散系数的增大图形单元间的距离增大。由于波数相等时两子系统的图灵模波数相同且地位相等,两波模无共振耦合发生,不会有新的失稳模产生,因此系统仅有单一空间尺度的简单斑图形成,二维傅里叶频谱显示具有一套矢量结构,呈六边形分布,且波形空间分布图中仅有一种强度波形。

图2 波数比为1时的简单六边形斑图Fig.2 Simple hexagon pattern when the wave number ratio is 1
波数比大于1时,两子系统图灵模地位不同,长波模处于主导地位,短波模受长波模调制(系统处于初级图灵分岔点附近,两模虽能发生耦合但不满足共振条件,图灵斑图受空间共振规律的约束,系统对失稳模的波长选择是单一的或一条较窄的波段,因此2个子系统呈现出相同单一空间尺度的简单斑图);在高级图灵分岔点附近,在一定条件下2个子系统图灵模会发生空间共振耦合,有新的失稳模产生,新生模与基模间形成三波共振或多波共振,从而在短波模所处的子系统中会形成复杂的图灵斑图。
图3是波数比为2时,短波模系统形成的超六边形斑图。从图3中可以看出不同模拟参数下两模线性耦合作用时可形成白眼超六边形,在非线性耦合作用下可形成环状超六边斑图,构成六边形的子单元不再是简单的一个点或线,而是由复杂结构的子单元构成,白眼超六边形斑图子单元中心为一白眼斑图周围有6个暗点,环状超六边斑图子单元从里到外由3层不同颜色圆环构成;二维傅里叶频谱分布图显示超六边斑图是由几套子结构构成,且不同层次波矢的波数不同;波形空间分布显示是由2种不同强度的波耦合而成。
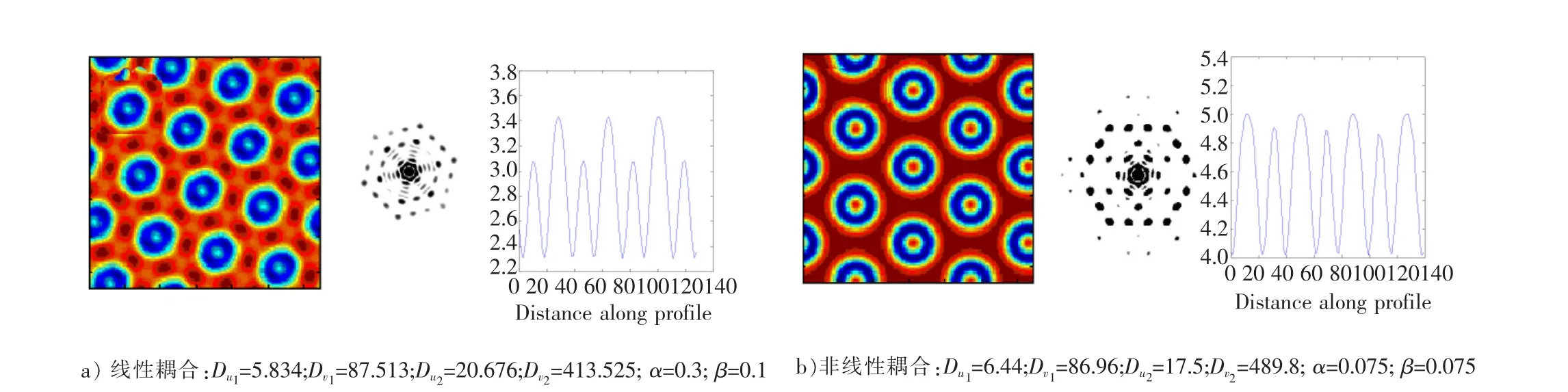
图3 波数比为2时的超六边形斑图Fig.3 Super hexagon pattern when the wave number ratio is 2
图4是波数比为3时,短波模系统形成的类蜂窝(图4 a1))和白眼斑图(图4 b1))。

图4 波数比为3时的类峰窝和白眼斑图Fig.4 Honeycomb-like and white-eye pattern when the wave number ratio is 3
在相同的模拟参数下两模在线性耦合作用时形成类蜂窝斑图,非线性耦合作用时形成白眼斑图,类蜂窝斑图的中心斑图与普通超六边形的子单元结构相同,边缘为短线相连形成的六边形边框,白眼斑图的每一个六边形晶胞中心为白色斑点,向外依次是一个暗环和亮环,形成类似于眼睛的结构,同样类蜂窝和白眼斑图的傅里叶频谱图是由几套子结构构成、波形空间显示出2种不同强度的波。从图4中分析可以看出复杂斑图不但受波数比的影响,还与两模耦合形式及强度有关,且通过对比模拟参数发现在非线性耦合作用时两模产生共振所需耦合强度一般小于线性耦合。
3 结 语
综上所述,利用双层四变量Lengyel-Epstein数值模型,通过两模在线性和非线性耦合的相互作用下获得了多种复杂斑图。模拟结果表明:只有两子系统图灵模的波数比大于1、两模发生共振耦合时,系统才有新的不稳定波矢产生,此时系统处在图灵高级分岔点附近,由于不稳定模具有2个或2个以上不同的波长,且不同波矢间满足三波共振关系,在短波模子系统中才能产生超点阵斑图。对于相同系统参数,线性耦合与非线性耦合方式系统出现的斑图式样不同,而且在非线性耦合作用时两模产生共振所需耦合强度一般小于线性耦合。本文模拟结果为深入研究各种复杂斑图具有一定的参考价值。
[1] SCHENK C P,OR-GUIL M,BODE M,et al.Interacting pulses in three-component reaction-diffusion systems on two-dimensional domains[J].Physical Review Letters,1997,78:3781-3784.
[2] BERENSTEIN I,DOLNIK M,YANG L F,et al.Turing pattern formation in a two-layer system:Superposition and superlattice patterns[J].Physical Review E,2004,70(4):046219.
[3] ARBELL H,FINEBERG J.Pattern formation in two-frequency forced parametric waves[J].Physical Review E,2002,65(3):036224.
[4] SHARPE J P,RAMAZZA P L,SUNGAR N,et al.Pattern stabilization through parameter alternation in a nonlinear optical system[J].Physical Review Letters,2006,96(9):094101.
[5] STOLLENWERK L,LAVEN J G,PURWINS H G.Spatially resolved surface-charge measurement in a planar dielectric-barrier discharge system[J].Physical Review Letters,2007,98(25):255001.
[6] BOIS J S,JÜLICHER F,GRILL S W.Pattern formation in active fluids[J].Physical Review Letters,2011,106(2):028103.
[7] DONG Lifang,FAN Weili,HE Yafeng,et al.Square superlattice pattern in dielectric barrier discharge[J].Physical Review E,2006,73(6):066206.
[8] YANG L F,DOLNIK M,ZHABOTINSKY A M,et al.Spatial resonances and superposition ptterns in a reaction-diffusion model with interacting turing modes[J].Physical Review Letters,2002,88(20):208303.
[9] DONG Lifang,LIU Weili,WANG Hongfang,et al.Honeycomb hexagon pattern in dielectric barrier discharge[J].Physical Review E,2007,76(4):046210.
[10] DUAN Xiaoxi,OUYANG Jiting,ZHAO Xiaofei,et al.Pattern formation and boundary effect in dielectric barrier glow discharge[J].Physical Review E,2009,80:016202.
[11] NIE Q Y,REN C S,WANG D Z,et al.Self-organized pattern formation of an atmospheric pressure plasma jet in a dielectric barrier discharge configuration[J].Applied Physics Letters,2007,90(22):221504.
[12] DONG Lifang,SHANG Jie,HE Yafeng,et al.Collective vibration of discharge current filaments in a self-organized pattern within a dielectric barrier discharge[J].Physical Review E,2012,85(6):066403.
[13] BARRIO R A,VAREA C,ARAGÓN J L,et al.A two-dimensional numerical study of spatial pattern formation in interacting turing systems[J].Bulletin of Mathematical Biology,1999,61(3):483-505.
[14] BERENSTEIN I,YANG Lingfa,DOLNIK M,et al.Superlattice turing structures in a photosensitive reaction-diffusion system[J].Physical Review Letters,2003,91(5):058302.
[15] DUAN X X,OUYANG J T,ZHAO X F,et al.Pattern formation and boundary effect in dielectric barrier glow discharge[J].Physical Review E,2009,80:016202.
[16] MÍGUEZ D G,DOLNIK M,EPSTEIN I,et al.Interaction of chemical patterns in coupled layers[J].Physical Review E,2011,84(4):046210.
[17] TURING A M,The chemical basis of morphogenesis[J].Bulletin of Mathematical Biology,1990,52(1):153-197.
[18] CROSS M C,HOHENBERG P C.Pattern formation outside of equilibrium[J].Reviews of Modern Physics,1993,65(3):851-1100.
[19] KYTTÄK,KASKI K,BARRIO R A.Complex turing patterns in non-linearly coupled systems[J].Physica A:Statistical Mechanics and Its Applications,2007,385(1):105-114.
[20] NI Weiming,TANG Moxun.Turing patterns in the Lengyel-Epstein system for CIMA reaction[J].Transactions of the American Mathematical Society,2005,357(10):3953-3969.
Analysis of Turing pattern in two-layer coupled Lengyel-Epstein model
BAI Zhanguo1,JING Honghua2,LI Xinzheng1,LI Yan1,LI Xinjuan1
(1.School of Science,Hebei University of Science and Technology,Shijiazhuang Hebei 050018,China;2.Institute for Vocational &Technical,Hebei Normal University,Shijiazhuang Hebei 050080,China)
The formation mechanism of Turing pattern is investigated by the two-layer coupled Lengyel-Epstein model.It is found that the coupling form and strength take an important role in the pattern formation under three wave number ratios between two Turing modes.When the wave number ratio is 1,the same simple pattern can be formed in the two subsystems(such as simple hexagon,quadrilateral and stripe pattern),and coupling coefficient and form have no effect on the pattern formation.When the wave number ratio is more than 1,the short wave mode subsystem can form a variety of superlattice patterns due to the resonance interaction between the two Turing modes:Two complex structures of super hexagon of white-eye and honeycomb-like appear in linear-coupling system,while superlattice patterns of super hexagon of circle and white-eye yield in nonlinear-coupling system.In addition,different coupling strength is required for resonance of Turing-mode in two-kind coupling forms.
Lengyel-Epstein model;Turing mode;couple;pattern
O415.3
A
1008-1542(2014)02-0134-05
10.7535/hbkd.2014yx02004
2013-10-28;
2013-12-12;责任编辑:张 军
国家自然科学基金(11247242);河北省自然科学基金(A2014208171);河北科技大学科研基金(QD201225,QD201226,SW09)
白占国(1971-),女,河北景县人,副教授,博士,主要从事等离子体物理及斑图动力学方面的研究。
E-mail:baizhanguo2011@163.com
