集中荷载作用下两端固支梁考虑SD效应的极限荷载分析

李 斌，韦成龙，李传习

(1. 湖南理工学院 土木建筑工程学院，湖南 岳阳 414006；2. 长沙理工大学 土木与建筑工程学院，湖南 长沙 410076)

梁是土木工程中广泛应用的结构，充分发挥其强度潜力具有重要的意义。许多学者在梁弹塑性阶段的受力、变形以及塑性极限荷载的求解方面做了大量工作[1-5]。如曹天捷，等[3]通过对挠度和弯矩关系进行积分得到含未知支反力的挠曲线方程，然后利用边界条件和连续性条件进行数值求解；李会知，等[4-5]利用虚功原理和单位荷载法研究了均布荷载作用下一次超静定梁在弹塑性加载过程中支反力与荷载的关系，并对集中荷载作用下两端固支超静定梁的全部弹塑性受力变形过程进行了分析。

但是，材料的拉伸与压缩屈服极限存在明显差异(即SD效应)[6-11]，塑性材料的压、拉屈服极限之比γ一般情况下为1～4/3。采用拉压强度相同的本构关系来分析梁各阶段受力、变形以及塑性极限荷载将给计算结果带来误差。为此，笔者选择集中荷载作用下的两端固支超静定梁，将材料本构关系简化成压拉屈服极限不同的理想弹塑性模型，利用结构对称性对SD效应影响的两端固支梁弹塑性加载及变形特点进行分析。根据截面上的弯矩值将梁划分为3个弹塑性发展状态不同的梁段，分别建立各种状态下的挠曲线近似微分方程。在对横截面中性轴进行确定的同时，给出了两端固支超静定梁在跨中集中荷载作用下弹塑性发展各阶段依赖于压、拉强度比的极限弯矩和位移公式。探讨了压、拉强度比对该超静定梁弯曲性能的影响。

1 受力变形特点分析

图1为两端固支超静定梁。假定材料为理想弹塑性材料，跨中作用集中力为F，压、拉屈服极限之比γ=σsc/σst>1，用σsc，σst分别表示材料拉、压屈服极限。梁截面为矩形，属于小柔度梁，可采用小变形理论分析，其等效结构如图2(a)。从变形和受力来说，该半结构又处于反对称状态，中点4截面的弯矩为0，其受力和变形可进一步等效于图3的静定悬臂梁。

图1 两端固支超静定梁Fig.1 Staticallay-fixed beam fixed at two ends

图2 l/2等效结构Fig.2 Equivalent force diagram of l/2

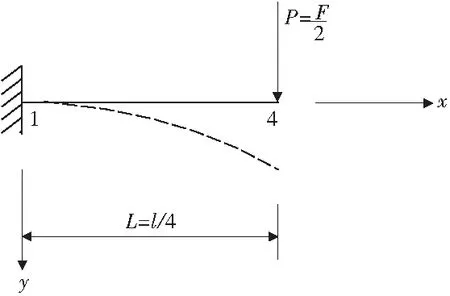
图3 等效悬臂梁Fig.3 Equivalent cantilever

超静定梁其他计算点处的内力和位移可以根据该等效悬臂梁的计算结果，对称计算得到。计算点7处的挠度y7=2y4，而其他各计算点处的挠度满足：y7+i=y7-i=y7-yi+1(i=1，2，3…，6)。

2 等效悬臂梁的弹塑性分析

为方便问题的描述，令P=F/2，L=l/4。逐级增大荷载，则等效悬臂梁的受力变形将经历以下3个阶段。

2.1 阶段Ⅰ

全梁处于弹性变形状态，梁竖向位移为：

(1)

式中：H1，H2为积分常数。

在本阶段，可以利用x=0处的位移及1阶导数为0的边界条件求得H1=H2=0。

2.2 阶段Ⅱ

逐级增大P，等效悬臂梁靠近固定端部分梁段进入单侧塑性状态，横截面上既有弹性区也有塑性区，在截面的弹性区内应力线性分布；塑性区内，应力等于屈服应力，如图4。取长度为dx的微段，横截面上的中性轴将偏离几何中轴，如图5。

图4 微段变形Fig.4 Deformation of micro-segment

图5 单侧塑性状态应力分布Fig.5 Stress distribution in unilateral plastic state

根据静力平衡条件：

(2)

(3)

以及横截面上任意点处的应变：

可得偏心距e、受拉弹性区高度d以及曲率半径ρ(x)，即：

(4)

(5)

在横截面上塑性区与弹性区的交界线y=d-e处，交界线上的应力已达屈服应力，则曲率半径可表示为：

(6)

将式(4)带入式(6)可得，单侧塑性状态下几何中轴挠曲线y(x)的近似微分方程为：

(7)

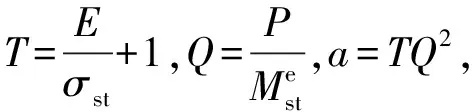
I1ξ+I2

(8)

式中：I1，I2为积分常数，可以利用x=0处的位移及1阶导数为0的边界条件确定：

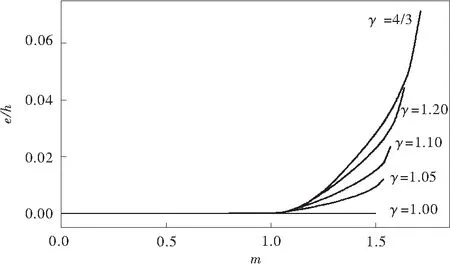
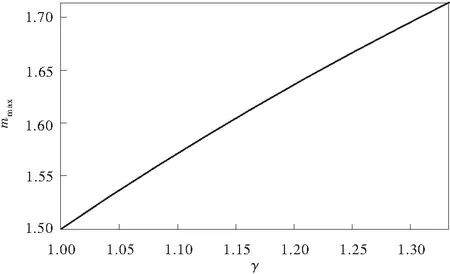
在完全弹性区域(x1≤x

Lx1) +I1

该阶段，横截面上最大压应力不大于屈服压应力，即：

(9)

2.3 阶段Ⅲ

等效悬臂梁靠近固定端部分梁段进入双侧塑性状态。此时，其他梁段部分处于单侧塑性状态、部分处于完全弹性状态，如图6。

图6 双侧塑性状态应力分布Fig.6 Stress distribution in bilateral plastic state

用阶段Ⅱ的方法，可由图6得到进入双侧塑性状态梁段截面处：

(10)

将式(10)代入式(6)，并引入变换ξ=Gx+A，可得双侧塑性状态下，几何中轴的挠曲线方程为：

(11)

在单侧塑性区域(x1≤x

同样，在完全弹性区域(x2≤x

3 算例及结果分析

以长800 cm、宽10 cm、高12 cm的矩形截面钢梁(坐标系及受力情况见图1)为例，研究SD效应对两端固支梁塑性极限弯矩Mu及变形的影响规律。材料σst=190 MPa，弹性模量E=200 GPa。

令γ分别等于4/3，1.20，1.10，1.05，1.00。分析SD效应对中性轴偏位、结构极限弯矩以及变形影响。

如图7，考虑SD效应时固定端(跨中)所在截面的中性轴偏位呈现有规律的变化(F的初值为11.4 kN，逐级增大至78 kN)，当m>1时(即进入阶段Ⅱ和阶段Ⅲ)，中性轴与截面几何中轴逐渐分离，且γ越大中心轴偏位越明显。若取γ= 4/3，偏心距e最大可达到0.071 37h。因此，笔者将坐标系原点建立在横截面的几何中轴上，为描述梁截面上任意点的位移带来了方便。

图7 SD效应引起的中性轴偏位Fig.7 Neutral axis deviation caused by SD effect

图8 γ对mmax的影响Fig.8 Effect of γ on mmax

图9 γ对跨中挠度wmax的影响Fig.9 Effect of γ on the deflection value wmax

与材料的σsc和σst的情况相比较，取γ=σsc/σst=4/3时塑性极限弯矩提高14.286%;而在同级荷载作用下(集中力F=68 kN，此时固端截面和跨中截面附近区域进入了阶段Ⅲ)，其跨中挠度减少16.804%。显然考虑材料的SD效应时，梁的抗弯能力提高，实际上是材料自身潜力的充分发挥。

各级荷载作用下两端固支梁考虑SD效应时(取γ=4/3)的弹塑性状态分布区间以及弹塑性发展全过程的挠曲线，可见表1及图10。

表1 各级荷载作用下梁的弹塑性状态分布区间

图10 各级荷载作用下梁的挠曲线Fig.10 Deflection curves of beam under loads

4 结 语

笔者利用结构对称性，对两端固支超静定梁在跨中集中荷载作用下考虑材料SD效应时的弹塑性加载全过程进行了分析。推导了理想弹塑性矩形截面梁几何中轴在完全弹性状态、单侧塑性状态及双侧塑性状态时的曲率方程，得到了悬臂梁几何中轴的曲率方程和位移方程。所得的解不仅能包含经典塑性理论的结果，而且能反映材料的压、拉强度差效应.分析可知，考虑材料SD效应时，中心轴在弹塑性加载过程中逐渐偏位，塑性极限弯矩和抗弯能力提高。因此，考虑材料SD效应可以得出更符合材料性质的极限荷载，可以更好的发挥材料的强度潜力，取得显著的经济效益。

[1] 伍小强,余同希.悬臂梁弹塑性大挠度全过程的分析[J].力学学报,1986,18(6):516-527.

Wu Xiaoqiang,Yu Tongxi.Analysis of the entire process of the large deflection of an elastic-plastic cantilever beam [J].Chinese Journal of Theoretical and Applied Mechanics, 1986, 18(6): 516-527.

[2] 干洪.梁的弹塑性大挠度数值分析[J].应用数学和力学,2000,21(6):633-639.

Gan Hong.Numerical analysis of the large deflection of an elastic-plastic beam[J].Applied Mathematics and Mechanics,2000,21(6): 633-639.

[3] 曹天捷,杜蓬娟.一次超静定理想弹塑性梁的全过程分析[J].工程力学,1999,16(3):105-112.

Cao Tianjie,Du Pengjuan.Analysis of the entire process of an elastic-plastic beam with one degree of indeterminacy [J].Engineering Mechanics,1999,16(3): 105-112.

[4] 李会知,刘敏珊,陈淮,等.均布荷载作用下一次超静定梁的弹塑性分析[J].工程力学,2006,23(10):86-90.

Li Huizhi,Liu Minshan,Chen Huai,et al.Elastic-plastic analysis of a beam with one degree of indeterminacy under an even load [J].Engineering Mechanics, 2006, 23(10): 86-90.

[5] 李会知,杨建中,李昊.集中荷载作用下两端固支梁的弹塑性力学解[J].郑州大学学报:理学版,2007,39(1):107-109.

Li Huizhi,Yang Jianzhong,Li Hao.The elastic-plastic solution of the beam fixed at two ends under a concentrated load [J].Journal of Zhengzhou University: Natural Science Edition, 2007, 39(1): 107-109.

[6] Theocaris P S.Yield criteria based on void coalescence mechanisms [J].International Journal of Solids and Structures, 1986, 22 (4): 445-466.

[7] Theocaris P S.A general yield criterion for engineering materials,depending on void growth [J].Meccanica, l986, 21(2): 97-105.

[8] 阮澍铭,张泽华,孙纲廷.拉压性能不同材料的几种结构的极限分析[J].应用力学学报,1996,l3(3):199-123.

Ruan Shuming,Zhang Zehua,Sun Gangting.Limit analysis of several structures which are made of materials having different behavior in tension and compression [J].Chinese Journal of Applied Mechanics,1996, l3(3):199-123.

[9] 王延斌,俞茂宏.拉压异性的简支圆板在线形分布荷载作用下的塑性极限分析[J].土木工程学报,2003, 36(8): 31-36.

Wang Yanbin,Yu Maohong.Plastic limit analysis of simply supported circular plates with different tensile and compressive strength under linear distributed load [J].China Civil Engineering Journal,2003,36 (8):31-36.

[10] Liang Yaping,Wang Huizhen,Ren Xingmin.Elastic-plastic limit analysis of combination cylinders made of S-D effect materials based on unified strength theory[J].Journal of University of Science and Technology of China, 2008, 38(4): 364-368.

[11] 阮澍铭.拉压性能不同材料全量型本构关系及环板的应力分析[J].烟台大学学报:自然科学与工程版,2002,l5(2):151-156.

Ruan Shuming.Deformation theory of constitutive equation for material with different behavior in tension and compression and analysis of annular plate [J].Journal of Yantai University: Natural Science & Engineering, 2002, l5(2): 151-156.