虎门桥主梁挠变之AR(P)模型分析
2014-03-01曾繁祥
曾繁祥,徐 兮
(1.重庆交通大学 土木建筑学院,重庆 400074;2.重庆育才工程咨询监理有限公司,重庆 400074)
虎门大桥是一座大跨径连续钢构桥,主梁施工采用的是挂篮悬臂浇筑工艺[1]。所谓挂篮悬臂浇筑,就是以桥墩为支点,使用悬吊的挂篮,对称地由两侧向跨中逐段现浇施工,最后完成桥跨段合龙的一种方法。显然,随着浇筑的逐步推进,主梁向中间相向延伸,其悬重和悬长必然不断增加,不间断地影响或改变着悬臂的施工状态,悬臂中的各梁块,在愈来愈大的荷载和张拉力的持续作用下,势必产生越来越大的挠变,若桥跨挠曲发展到超限的程度,轻则降低合龙精度,重则引发重大质量、安全事故。为使主梁的合龙精度满足相关规范和技术标准的要求,需要调整悬臂使之尽可能稳定地接近设计状态[2],而调整的依据,必须是可靠的,同时是事前的。
由于时间序列分析法中的AR(P)模型,是一种稳健度、可转移度、条理度都较高的模型,且具有较强的预报能力,应用时只需将对象的监测值作变量建立模型,即可预测同一对象将来的变形程度与发展规律[3],将其作为边施工边测量边预报的大跨径桥主梁的控制理论,无疑是十分合适的。
1 AR[P]模型
1.1 参数估计
有观测列x1,x2,…,xn,模型为P阶,则数据列中元素与前P个元素组成回归关系[2]如式(1):
(1)

令 :
(2)
与式(2)相应的误差估值方程组为:

(3)

(4)
参数φ的最小二乘估值为:
(5)
1.2 模型定阶
据AR(P)模型定阶理论[3],建立检验统计量如式(6):
(6)

选显著水平α,以分子自由度为2,分母自由度为n- 2P,由F分布表得Fα。若F>Fα,表示P阶与P-1阶两模型有显著差别,应采用P阶;反之,两模型无显著差别,应采用P-1阶。
1.3 预报模型
AR(P)模型的分步预报方程如下[4]:
(7)
(8)
2 实例分析
虎门大桥19号墩上游桥边跨20~23号块的实测挠度数据,列于表1[1]。

表1 挠曲变化分析
以块件编号为横坐标、挠度为纵坐标,绘出1线的20~23号块段挠变曲线(图1)。

图1 挠曲变化Fig.1 Deflection change
需要说明的是,AR(P)模型的定阶问题,本应按1.2节方法解决,但这就至少需要7个变量数据,目前数据量不足,因此暂取2阶,待数据量满足后,再计算验证取值正确与否。
由式(7)可知预报方程[5-7]:
(9)
由式(2)得式(10):
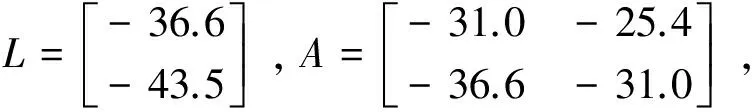
(10)

完成后,测得实际下挠值为-50.5 mm;由式(7)算得v5=-3.819 75;然后将上述数据填入表1,并在图1中延绘1线、点绘2线(预报曲线)的24号块之点。
同理,可以依次计算得到后续每一梁块的预报挠度,并据此调整悬臂放样高程,并顺序完成各梁块浇筑—测量u—求v—填表—延绘1、2线的工作(见表1、图1)。
3 P取值的验证
以1.2节方法,运用20~28块的挠度实测值(n=9),算得=0.904;取α=0.05,P=3,分母自由度为3(n-2P=9-2×3=3),查F分布表,得Fα=19.16。显然F 从表1的一系列回归残差v值看出[8],绝对值最大为-1.7,较《规范》规定的,高差误差允许值±20 mm,显然小许多;再者,图1的1线反映的是挠变实况,明显呈现线性规律;2线是挠变预测图像,明显亦呈现线性,并与1线吻合得十分好。从两个侧面说明挠度预报精度非常高。 相邻梁块挠度实测值互差、预报值互差均未大于20 mm,且无突变;图1的1、2两线线形均平顺光滑,都证实浇筑悬臂放样高程设置合理、调整程度恰当。 综上所述,判定本例工程全程安全,挠变监控整体有效,同跨合龙精度严格满足设计要求及《规范》规定。 在箱梁桥桥跨挂篮悬臂浇筑施工中,以AR(P)模型为平台,进行挠度监控数据处理,一方面让施工中的调整事前、有据,另一方面表明自回归理论具备实用、严谨的优势。 [1] 牛和恩.虎门大桥工程[M].北京:人民交通出版社,1998. Niu He’en.The Humen Bridge [M].Beijing:China Communications Press,1998. [2] 吴怀宇.时间序列分析与综合[M].武汉:武汉大学出版社,2004. Wu Huaiyu.Time Series Analysis and Synthesis [M].Wuhan:Wuhan University Press, 2004. [3] 白凤山,么焕民,李春玲.数学建模[M].哈尔滨:哈尔滨工业大学出版社,2003. Bai Fengshan,Yao Huanmin,Li Chunlin.Mathematical modeling [M].Harbin: Harbin Institute of Technology Press, 2003. [4] 徐兮,曾繁祥.箱梁桥悬臂施工挠度控制的回归方法[J].数学的实践与认识,2010(8):103-105. Xu Xi,Zeng Fanxiang.Regression analysis methods for deflection Controlling of box girder Bridge cantilever [J].Mathematics in Practice and Theory, 2010(8): 103-105. [5] 岳建平,方露,黎昵.变形监测理论与技术研究进展[J].测绘通报,2007(7):1-4. Yue Janping,Fang Lu,Li Ni.Research advances of theory and technology in deformation monitoring[J].Bulletin of Surveying and Mapping, 2007(7): 1-4. [6] 何晓群,刘文卿.应用回归分析[M].北京:中国人民大学出版社,2001. He Xiaoqun,Liu Wenqing.Applied Regression Analysis [M].Beijing: China Renmin University Press, 2001. [7] 郑少华,姜奉华.试验设计与数据处理[M].北京:中国建材工业出版社,2004. Zheng Shaohua,Jiang Fenghua.Experiment Design and Data Processing [M].Beijing: China Building Materials Press, 2004. [8] 曾山,徐兮.隧拱变形分析的自回归与分段回归方法应用[J].重庆交通大学学报:自然科学版,2013,32(3):442-445. Zeng Shan, Xu Xi.Application of auto-regression and subsection-regression method in tunnel deformation analysis[J].Journal of Chongqing Jiaotong University:Natural Science, 2013, 32(3): 442-445.4 分 析
5 结 语
