非均匀预应力筋束非线性松弛损失研究

彭 凯，于丛丛

(重庆交通大学 土木建筑学院，重庆 400074)

预应力筋松弛与混凝土徐变同是影响预应力混凝土结构应力损失和长期工作性能的基本问题之一[1-2]。目前对常规条件下单根高强钢丝、钢绞线的松弛性能研究已经较为全面和充分[3-6]，国内外相关的设计技术规范发展也较为成熟[7-11]。当前预应力筋松弛问题的研究更加关注各种特殊环境因素或使用条件，如建筑火灾引起的高温环境[12]，加工、运输过程造成的残余应力[13-14]，以及施工及使用过程温度、应力变化[15]等对预应力筋松弛损失的影响。其中比较严峻的一个现实问题是，在实际结构中预应力筋往往成束使用，而实测数据显示[16]，由于预应力施工技术要求较高、过程控制难度较大，预应力筋张拉锚固时刻筋束内各根力筋初应力均匀性难以保障，部分力筋锚固初应力偏离筋束平均初应力较大，甚至会因为接近或超过屈服点发生过大松弛或长期强度降低。鉴于单根预应力筋松弛损失对初应力的敏感性和两者之间的非线性关系[3-6]，对实际结构中的非均匀预应力筋束，如果仍按预应力筋束平均初应力值计算其松弛损失，很有可能造成预应力松弛损失估计偏差较大。这在一定程度上可视为近年来国内外频繁出现的预应力混凝土结构有效预应力长期损失过大、开裂、下挠失控等诸多预应力相关病害现象[1-2]的主要原因之一，值得在预应力结构设计和施工中予以重视。

1 单根预应力筋的松弛规律及预应力筋成束使用存在的问题

1.1 单根预应力筋的松弛规律

现有国内外研究成果表明[3-6]，就单根预应力筋(高强钢丝或钢绞线)而言，初应力水平是影响常温下预应力钢筋松弛性能的最主要因素之一。力筋松弛率随着初应力水平的提高呈非线性增大的趋势。根据文献[6]的试验数据，得到在不同时间长度内力筋松弛率R与初始应力水平σi/fpk(σi为力筋初应力，fpk为力筋抗拉强度标准值)之间的关系，如图1。

图1 低松弛钢丝松弛率与σi/fpk关系曲线Fig.1 Relationship between σi/fpk and relaxation ratios of low-relaxation prestressing steel wires

由图1可见，σi/fpk= 0.5～0.6时，松弛率R基本不变；σi/fpk= 0.6～0.7时，松弛率R的增长逐渐加快；σi/fpk= 0.7～0.8时，即接近或超过钢绞线的比例极限(对应的σi/fpk≈0.75)时，松弛率R急剧增大，表现出明显的非线性。

美国加州交通局针对预应力钢绞线开展过常温下的松弛实验[17]，分别对两根ASTM 1 860 MPa级钢绞线试件施加相当于82.3%和67.8%极限抗拉强度的初应力后保持长度72 h，得到了如表1的试验结果。

表1 不同初始应力下72 h内钢绞线发生的松弛损失

表1显示，在72 h内，初应力水平大小不同的两根钢绞线的松弛应力损失分别达到各自初应力的23.5%和3.6%，前者应力松弛损失率是后者的6.5倍，松弛损失绝对值是后者的7.9倍。可见，预应力筋的松弛应力损失对初应力水平非常敏感，尤其当预应力筋的初应力接近或超过比例极限时，松弛损失将急剧增加。究其原因，可归结为此时钢筋塑性变形的明显增加。

在总结前期实验和理论研究成果的基础上，现有各国预应力结构设计规范[7-11]给出了计算预应力钢筋松弛损失的较为类似的公式。以我国交通行业JTG D 62—2004《公路钢筋混凝土及预应力混凝土桥涵设计规范》[10]为例，其中计算预应力钢丝、钢绞线松弛损失终极值的公式为：

(1)

式中：ψ为张拉系数，一次张拉时，ψ=1.0，超张拉时，ψ= 0.9；ξ为 钢筋松弛系数，I级松弛(普通松弛)，ξ=1.0，II级松弛(低松弛)，ξ= 0.3；σpe为传力锚固时的钢筋应力。

由式(1)可见预应力筋松弛损失与传力锚固时的钢筋应力存在明显的非线性关系。

1.2 预应力筋束松弛损失计算存在的问题

目前在实际结构中预应力筋往往成束使用。国内外相关设计规范[7-11]对预应力筋松弛估算的规定中，均隐含有这样一条假定：多根预应力筋组成的预应力筋束松弛率等效于具有筋束平均初应力水平的单根预应力筋的松弛率，也即在给定时刻计算预应力筋束的松弛力值等效于具有筋束平均初应力水平的单根预应力筋的松弛力值按照该筋束所含根数线性放大。然而，一旦预应力筋束内部分预应力筋锚固初应力接近或超过其条件屈服强度，其松弛损失将大大超过按照筋束平均初应力水平估算的松弛损失值。更有甚者，预应力筋受过高应力长期持续作用可能会发生塑性应变过大、疲劳强度降低而断裂，而且这一过程可能引发连锁反应：同一束力筋一部分高应力钢绞线的疲劳断裂会造成余下钢绞线应力集中，上述高应力松弛效应有可能会逐根传递[16]。

因此，在同一束非均匀预应力筋束内，在其他条件不变的情况下，由于各根力筋锚固初应力水平分布不均匀，其对应的给定时段内松弛率分布也不均匀，且松弛率与初应力水平之间存在明显的非线性关系，若将单根预应力筋试验得到的应力松弛模型直接线性推广到非均匀预应力筋束并按其平均初应力水平估算束力长期松弛损失，从理论上看存在较大疑点，在实践中也可能造成不利的结构效应。这也正是笔者研究的核心问题。

2 实测预应力筋束锚固初应力分布及松弛损失计算

针对上述问题，笔者基于某桥梁施工现场预应力筋束内各单根钢绞线(ASTM 1 860 MPa级低松弛钢绞线)锚固初应力实测数据开展研究。表2所列为其中3束预应力筋(张拉控制应力σcon=0.75fpk，有超张拉)传力锚固后12 h内单根钢绞线锚下初应力实测值σi及其与钢绞线抗拉强度fpk的比值σi/fpk。

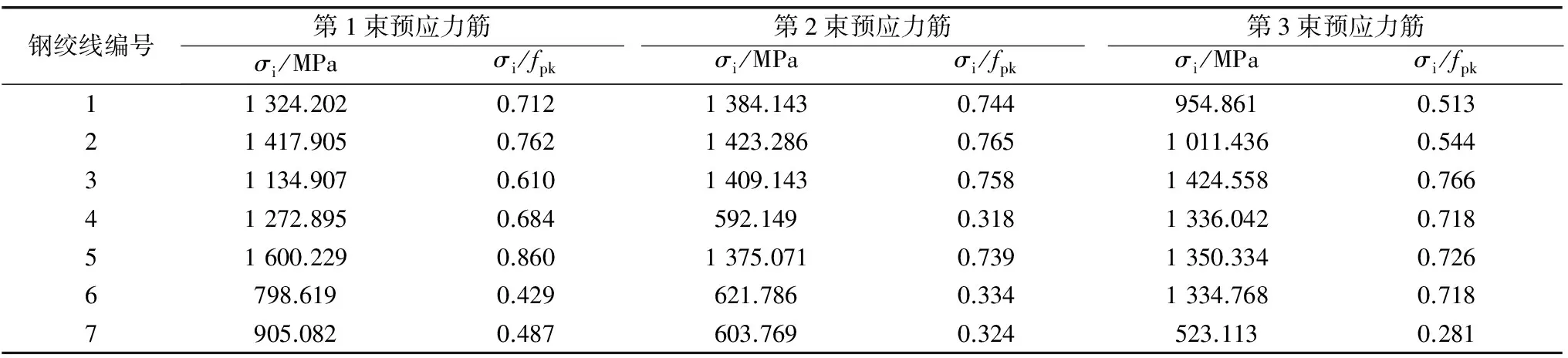
表2 传力锚固后12h内各单根钢绞线σi及σi/fpk(fpk = 1 860 MPa)

表2数据显示，设计张拉控制应力σcon= 0.75fpk时，同束预应力筋传力锚固后，相应的锚具变形回缩及构件弹性压缩等引起的预应力损失已经发生，此时测得的筋束内部分钢绞线锚下初应力仍然超过张拉控制应力，有的甚至达到0.860fpk；另有部分钢绞线锚下初应力偏小，甚至低至0.281fpk。这表明现有施工条件下预应力筋束锚下初应力的分布可能具有严重的非均匀性，其对筋束松弛损失的影响尚未引起足够重视。表3所列为考虑锚下初应力分布非均匀性，对表2中第2束预应力筋根据式(1)，分别按各单根钢绞线锚固初应力及筋束平均锚固初应力计算得到的筋束应力松弛损失结果。

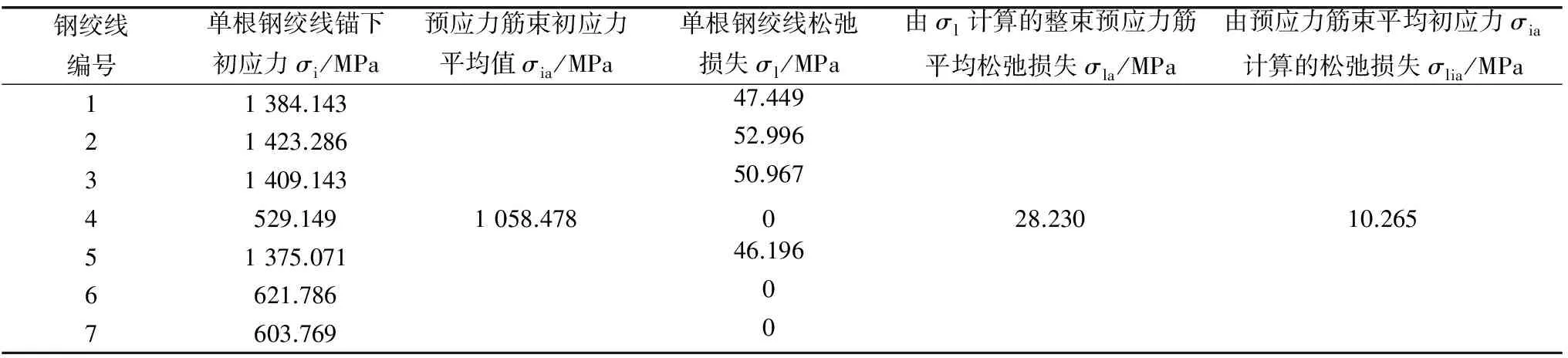
表3 考虑预应力筋束初应力分布非均匀性的松弛损失计算结果

由表3可见，由σl计算的整束预应力筋的平均松弛损失σla为28.230 MPa；由预应力筋束平均初应力σia计算的松弛损失σlia为10.265 MPa。前者大约是后者的2.75倍。这一结果表明：鉴于预应力筋束内各单根力筋初应力分布的不均匀性及力筋松弛损失与初应力水平之间的非线性关系，按照具有筋束平均初应力水平的单根力筋的松弛损失线性增大(即直接乘以筋束内力筋根数)得到的整束预应力筋的松弛损失，与按照筋束内各单根力筋非均匀初应力分布计算得到的整束预应力筋松弛损失之间，可能会出现成倍的误差。

为此，通过对预应力筋束内各根力筋锚固初应力分布的概率描述和随机数模拟，对非均匀预应力筋束松弛损失的计算误差开展进一步研究。

3 非均匀预应力筋束松弛损失计算误差的参数分析

根据实测数据统计分析，同一束预应力筋传力锚固时各根钢绞线初应力大致呈正态分布。因此，可以通过调整正态分布概率模型的参数，借用现有成熟的随机数生成方法来模拟预应力筋束内各根力筋的初应力分布特性，用于非均匀预应力筋束松弛损失计算误差的参数分析。根据某特大型预应力混凝土梁桥51号墩左幅14号块孔号1预应力筋束(含30根钢绞线，σcon= 0.75fpk)内各根钢绞线锚固初应力实测值，采用Excel软件随机数生成功能模拟其分布，二者对比见图2。采用离散系数(离散系数δ=标准差σ/平均值μ)表示同一筋束内各根力筋锚固初应力的非均匀程度。

图2 同束预应力筋内钢绞线锚固初应力实测值分布的随机模拟Fig.2 Stochastic simulation of strands’initial stress distribution for a prestressing steel bundle

针对一束含7根钢绞线的预应力筋束，利用图2的随机模拟方法，分别调整离散系数δ和平均值μ的取值，得到多组力筋锚固初应力分布样本，再按照表3计算各根钢绞线松弛损失平均值σla，并由预应力筋束平均初应力σia计算松弛损失σlia，在此基础上建立δ，μ与松弛损失比值σla/σlia之间的关系(图3)，借以考察预应力筋束内各根力筋初应力非均匀分布特性对松弛损失计算误差的影响。

图3 筋束内钢绞线初应力平均值和离散系数δ对σla/σlia的影响Fig.3 Effect of strands’initial stress dispersion coefficients δ and average values on σla/σlia in prestressing bundles

如图3，随机模拟中预应力筋束平均初应力值μ取1 039.89～1 299.87 MPa，μ与对应张拉控制应力σcon的关系由实测数据统计得到，列于表4。离散系数δ在区间(0, 0.5)取值。

表4 不同张拉控制应力下的钢绞线锚固初应力

由图3，在不同的筋束平均初应力值μ条件下，随δ值的增大，比值σla/σlia均呈现非线性增长趋势，且μ值越大增速越快。即非均匀预应力筋束的松弛损失若按照常规的取筋束平均初应力进行计算，其误差将随着筋束内初应力离散系数的增加而非线性增大；同样的筋束内初应力离散系数下，张拉控制应力越大，松弛损失的计算误差越大。

在实际预应力结构中，取决于设计要求的预应力锚具和管道的规格，一束预应力筋内钢绞线根数N一般在2～30范围内变化。其他条件不变，非均匀预应力筋束内钢绞线根数对筋束松弛损失的计算误差的影响应予以考察。按照前述随机模拟方法，计算得到预应力筋束内钢绞线不同根数N及离散系数δ对σla/σlia的影响关系见图4(计算取σcon= 0.70fpk)。

图4 筋束内钢绞线根数N和离散系数δ对σla/σlia的影响Fig.4 Effect of strands’quantity N and dispersion coefficients δon σla/σlia in prestressing bundles

图4中，在离散系数δ取0～0.5(实际问题中δ值一般不会超过0.5)时，预应力筋束内钢绞线根数N取不同值计算得到的δ-(σla/σlia)曲线基本重合。采用其他σcon值计算会得到类似结果，限于篇幅，不再图示。这表明预应力筋束内钢绞线根数N对初应力非均匀性造成的松弛损失计算误差影响不大。

4 预应力筋松弛损失计算误差的拟合估计及控制建议

为方便工程应用，图3所示预应力筋束在不同张拉控制应力下初应力离散系数对筋束松弛损失计算误差的影响关系随机模拟结果，可采用多项式进行拟合。对应于σcon= 0.75fpk，0.70fpk，0.65fpk拟合得到的δ- (σla/σlia)关系式分别为式(2)～式(4)。与图3相对应，式(2)～式(4)适用的离散系数δ取值区间为(0，0.5)：

σla/σlia=22.313 0δ2-1.194 7δ+1.050 0

(2)

σla/σlia=5.763 6δ2+0.245 4δ+0.963 8

(3)

σla/σlia=3.967 0δ2-0.234 3δ+0.993 0

(4)

对于σcon< 0.65fpk的情形，由图3可见，其对应的δ-(σla/σlia)曲线与σcon= 0.65fpk对应的δ-(σla/σlia)曲线很接近，可直接利用后者的拟合结果。

根据式(2)～式(4)，将δ-(σla/σlia)关系多项式拟合结果示于图5，可见各多项式拟合误差均很小(相关系数分别为0.982 7，0.972 8，0.971 2)，方便在实际的预应力结构设计、施工中用来估计预应力筋束松弛损失计算误差并予以修正。

图5 δ-(σla/σlia)关系的多项式拟合Fig.5 Polynomial fitting of δ-(σla/σlia)

此外，在现有技术经济条件下，在预应力工程施工中如何尽量提高施工质量，将预应力筋束锚固初应力的离散系数δ控制在合理的范围内，才是解决非均匀预应力筋束松弛损失过大的根本途径。由图3、图5可见，当δ≤0.1时，σla/σlia≈ 1，也即此时采用规范[3]的筋束松弛损失计算方法已足够精确，误差很小。因此，建议在预应力施工中通过引入过程监测控制方法[16]，将预应力筋束锚固初应力的离散系数δ控制在0.1以内。如现有经济和技术条件达不到上述控制目标，则应在设计和施工中根据实际情况，按式(2)～式(4)估计非均匀预应力筋束松弛损失计算误差并予以修正。

5 结 论

笔者就预应力筋束锚固初应力分布的非均匀特性，对筋束松弛损失的影响及其控制开展研究，主要结论如下：

1)实测数据表明，现有施工条件下预应力筋束锚固初应力分布的非均匀性不可忽略，对筋束松弛损失的计算误差影响应予以重视。

2)预应力筋束锚固初应力样本可采用正态分布模型予以近似描述和随机模拟。

3)预应力筋束锚固初应力离散系数δ对筋束松弛损失计算误差的影响关系具有明显的非线性特征，δ值越大，误差值和误差增速越大；该影响关系可采用多项式进行较好的拟合。

4)在实际工程应用中，建议通过施工质量控制手段将预应力筋束锚固初应力离散系数δ控制在0.1以内，否则可按笔者推荐公式对筋束松弛损失的计算误差进行估计和修正。

[1] 王敏.从预应力损失角度对混凝土桥梁病害成因的研究[D].武汉:武汉理工大学,2005.

Wang Min.Research on the Disease Cause of Concrete Bridge From Pre-Stress Loss [D]. Wuhan: Wuhan University of Technology, 2005.

[2] 黄雅宁,周水兴,王艳,等.新旧规范对预应力连续刚构桥线形影响分析[J].重庆交通大学学报:自然科学版,2010,29(2):174-176.

Huang Yaning, Zhou Shuixing,Wang Yan,et al.Deck layout influence of continuous rigid-frame bridge between updated and old specification[J].Journal of Chongqing Jiaotong University:Natural Science, 2010, 29(2): 174-176.

[3] Magura D D,Sozen M A,Siess C P.A study of stress relaxation in prestressing reinforcement [J].PCI Journal, 1964, 9(2): 13-57.

[4] 高伯阳.预应力高强度钢丝和七股钢绞绳的徐变及应力松弛试验[J].土木工程学报,1964(2):30-40.

Gao Boyang.Experiment on creep and stress relaxation of prestressing high-strength steel wires and 7-wire steel strands [J].China Civil Engineering Journal, 1964(2): 30-40.

[5] 陆光闾.预应力高强钢丝松弛性能研究[J].土木工程学报,1997,30 (6):41-46.

Lu Guanglv.Study on the stress relaxation in prestressed wires[J].China Civil Engineering Journal, 1997, 30(6): 41-46.

[6] 陆光闾.低松弛预应力钢丝松弛性能研究[J].上海铁道大学学报:自然科学版,1997,18(2):46-52.

Lu Guanglv.Experiment study on the stress relaxation in low relaxation prestressing wires [J].Journal of Shanghai Tiedao University:Natural Science,1997,18(2): 46-52.

[7] Comite Euro-International du Beton.Bulletin D.information No.213/214 CEB-FIP Model Code 1990:Concrete Structures[S].Lausanne,Switzerland: Comite Euro-International du Beton,1993.

[8] AASHTO.LRFD Bridge Design Specifications:SI Units[S].3rd ed.Washington,DC: AASHTO, 2005.

[9] GB 50010—2010 混凝土结构设计规范[S].北京:中国建筑工业出版社,2010.

GB 50010—2010 Code for Design of Concrete Structures [S].Beijing: China Architecture & Building Press, 2010.

[10] JTG D 62—2004 公路钢筋混凝土及预应力混凝土桥涵设计规范[S].北京:人民交通出版社,2004.

JTG D 62—2004 Code for Design of Highway Reinforced Concrete and Prestressed Concrete Bridges and Culverts [S].Beijing: China Communications Press, 2004.

[11] TB 10002.3—2005铁路桥涵钢筋混凝土和预应力混凝结构设计规范[S].北京:中国铁道出版社,2005.

TB 10002.3—2005 Code for Design on Reinforced and Prestressed Concrete Structure of Railway Bridge and Culvert [S].Beijing:China Railway Publishing House, 2005.

[12] 张昊宇,郑文忠.高温下1770级φP5钢丝蠕变及应力松弛性能试验研究[J].土木工程学报,2006,39(8):7-13.

Zhang Haoyu, Zheng Wenzhong.An experimental study on the creep and stress relaxation properties of 1770 φP5 prestressing steel wires at high temperatures [J].China Civil Engineering Journal, 2006, 39(8): 7-13.

[13] Atienza J M,Elices M.Role of residual stresses in stress relaxation of prestressed concrete wires [J].Journal of Materials in Civil Engineering, 2007, 19(8): 703-708.

[14] Elices M,Suarez F,Gálvez J C,et al.Influence of coiling on the stress relaxation of prestressing steel wires[J].Structural Concrete,2011, 12(2): 120-125.

[15] 姚慧芳,陈德荣,王钦堂.高强钢丝和钢绞线松弛问题探讨[J].公路交通技术, 2007 (3):134-136.

Yao Huifang,Chen Derong,Wang Qintang.Discussion on high strength steel wire and steel strand slack [J].Technology of Highway and Transport,2007(3):134-136.

[16] 王继成,向中富,彭凯,等.桥梁预应力及索力张拉测控技术[M].北京:人民交通出版社,2010.

Wang Jicheng,Xiang Zhongfu,Peng Kai,et al.Measurement and Control Technology for Tensioning of Bridge Prestress and Cable Force[M].Beijing: China Communications Press, 2010.

[17] Department of Transportation,State of California.Prestress Manual[E/OL].Sacramento: Department of Transportation, State of California, 2005[2013-06-01]http://dot.ca.gov/hq/esc/construction/manuals/.