基于路径提取的旋转模糊图像复原算法
2014-03-01罗院红许廷发朱振福
罗院红,许廷发,朱振福
(1.北京理工大学 光电学院 光电成像技术与系统教育部重点实验室,北京100081;2.北京环境特性研究所 目标与环境光学特征国防科技重点实验室,北京100854)
0 引言
随着传感器成像技术的发展,越来越多的光学成像传感器安装在运动平台上。当光学传感器随着旋转平台作高速旋转运动时,在传感器成像的曝光时间内,由于光学传感器与场景之间存在较大的相对运动,所获取的图像将会产生严重的旋转模糊。模糊图像给后续的视频图像跟踪处理,包括目标检测、识别和跟踪带来很大的困难,因此,有效地对旋转模糊图像进行复原是视频图像跟踪的一项重要工作。
国内外针对旋转模糊图像的复原问题已开展了一些相关的研究。Sawchuk[1-2]使用极坐标变换的方法,将二维直角坐标系下的图像变换到极坐标下,这样直角坐标系下的图像旋转模糊在极坐标下就变成旋转角θ 方向的直线运动模糊,缺点是要进行两次坐标变换和两次灰度插值,运算量很大而且容易丢失原始图像信息。洪汉玉等[3-4]提取一种基于Bresenham 路径提取的最小二乘复原算法,该算法避免了坐标变换的繁琐运算,但是最小二乘算法运算量仍然较大,且容易产生高频振荡,不利于实时实现。
为了避免大量的坐标变换和灰度插值运算,本文提出一种基于模糊路径的图像复原方法。这种方法通过数据分离,将二维图像旋转模糊复原转换为一维的反卷积复原。本方法能够快速地复原提取后的一维数据;能够解决旋转角度较大时的图像复原问题,且速度较快,能达到实时性的要求。
1 旋转模糊退化模型
旋转图像模糊不同于直线运动模糊,旋转模糊是沿路径的径向运动模糊。其模糊长度随半径的变换而变化,即离旋转轴心越远,模糊长度越长。原始图像的象素灰度值沿以旋转轴心为圆心的一系列同心圆路径在像平面内进行模糊,称这一系列同心圆路径为模糊路径。
电荷耦合元件(CCD)成像的过程其实就是像素灰度的积分过程,而图像模糊就可看成是场景中运动轨迹上若干个点的能量在CCD 像平面上的积累,设清晰图像为f(x,y),旋转模糊图像为g(x,y),则在曝光时间T 内,实际采集的模糊图像g(x,y)与清晰图像f(x,y)的关系可表述为

采用极坐标表示为

为了便于离散化处理,将弧长l =rθ 来代替角度θ 坐标,并令s=rωt,ar=rωT,则有
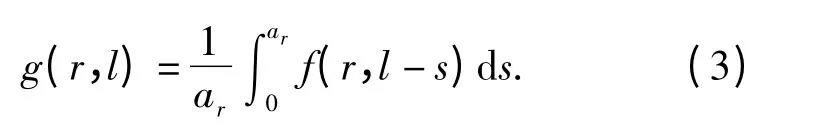
将(3)式沿模糊路径分离并进行空间离散化后可得

式中:gr(i)为模糊图像的像素灰度值;fr(i)为清晰图像像素灰度值;Nr为圆周上像素的总数。这样就将二维图像的旋转模糊问题转化为一维的直线运动模糊问题。gr(i)即是对应半径为r 的图像数据,其中ar为沿模糊路径的模糊长度。
观察(4)式,将fr(i)周期延拓,即有fr(i)=fr(i +Nr);并定义对应于半径为r 时的一维点扩散函数可将其写成离散卷积的形式:
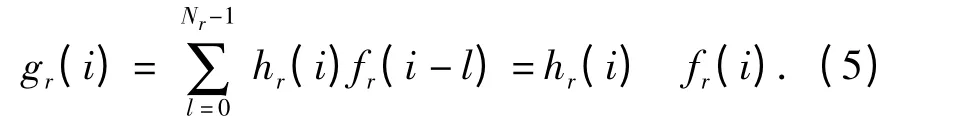
写成矩阵形式,有g=Cf,其中C 是点扩散函数hr(i)的循环矩阵。引入噪声项,则基于模糊图像的退化模型为

这样就将二维的旋转模糊复原问题转化为模糊路径上一维数据的复原,而同一模糊路径上的模糊是空间不变的,即同半径上的图像像素模糊长度相同,具有相同的点扩散函数。因此,为了复原图像,可以逐一地沿圆周模糊路径反卷积去模糊。
2 模糊路径提取
由第1 节的理论推导可知,旋转模糊复原首先要提取模糊路径上的象元灰度值。传感器成像是将场景中的能量信息记录在二维的离散像平面上,离散平面上的像素点并不在标准的圆周上,如图1(a)所示。一种可行的方法是用双线性差值将离散直角坐标上的像素值转化到圆周上,但这种方法难免导入复杂的运算,计算量大。因此本文使用最小偏差圆弧插补法来提取模糊路径,提取的模糊路径为近似圆周,见图1(b).
本文结合最小偏差圆弧插补算法和图像旋转模糊原理[5-6],用插补法提取1/4 圆弧的模糊路径,根据对称性求得其他3 个象限模糊路径。提取的路径如图1(b)所示,并非理想的标准圆,但插补法提取的路径上的点与理想圆弧的误差小于0.5 个像素点,而图像灰度值是高度相关法的,所以模糊路径上的各像素点与理想圆周上点的像素值非常接近。最小偏差插补法只需要在步进时进行简单的误差判断,避免了三角函数、开方等复杂的运算,大大减少了计算量。
最小偏差插补法在给定运动模式下能够提取任意轨迹的路径,包括直线、圆弧和非圆弧曲线,所以在图像旋转模糊路径为非正规圆时,也可以用最小偏差插补法提取模糊路径。也就是在旋转轴心不稳定的情况下,最小偏差插补法提取路径仍然有效,仍可以在模糊路径上复原图像,这种能力是极坐标变化法所不具备的。
3 旋转模糊图像复原模型
3.1 维纳滤波复原模型
对于上述的一维图像模糊数据可用一维的维纳滤波复原。基于卷积定理,对(5)式作傅里叶变换,转换为频域,有

图像噪声可以看作是随机过程,图像复原其实就是一个基于统计估计的数据复原过程。维纳滤波就是找一个原图像f 的估计值,使得它们之间的均方误差最小,即使e2=E{(f-)2}最小。由此可推导,维纳滤波得到一维复原数据的频谱[7-8]:


图1 基于最小偏差圆弧插补的模糊路径提取方法Fig.1 Trail extraction based on circular minimum deviation interpolator
式中:k(u)=Sn(u)/Sf(u),Sn和Sf分别表示噪声和未退化图像的功率谱,由于未退化图像的功率谱无法精确获取,所以常采用信噪比作为参数,k(u)=1/SNR,SNR =(Sg-Sn)/Sn,Sg为模糊图像的功率谱,因此通过计算模糊图像和噪声的功率谱,即可获维纳滤波参数。实际模糊图像复原过程中,综合考虑算法的实时性和有效性,对于同一传感器的图像,往往在初始运算过程中通过计算某一幅图像的信噪比,进而获取维纳滤波参数k,后续的图像复原都使用该滤波参数进行复原,即采用常量维纳滤波复原图像。
3.2 对角加载算法复原
3.2.1 对角加载算法原理
对角加载算法主要是源于对逆滤波的改进。退化后的一维图像数据可表示为g =Cf,C 就是退化矩阵,为一循环矩阵。无约束的代数法复原可得,复原数据C-1g,对循环矩阵C 对角化后可推导得,,这就是逆滤波。
由于矩阵C 具有零特征值或小特征值,C 具有零特征值时C 不可逆,具有小特征值时,求逆会带来严重的震荡。所以逆滤波会产生严重的病态问题。一种解决矩阵病态性的方法是对角加载技术,修正循环矩阵C[9]。修正后的矩阵为C' = C +ΔλI,可证明C'的特征值变为ξ(k)= λ(k)+ Δλ,λ(k)是原循环矩阵C 的特征值。
证明1 C'的特征值E(C')=E(C +ΔλI)=E(C)+E(ΔλI)=E(C)+ΔλE(I),由于E(C)=λ(k),所以E(C')=λ(k)+Δλ. 即修正后循环矩阵的特征值为λ(k)+Δλ,且C'只是改变原矩阵C对角元素的值,所以修正后的矩阵仍然为循环矩阵。
修正前的循环矩阵为
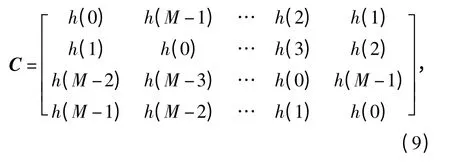
修正后的矩阵为

显然,C'仍然是循环矩阵,所以仍然可以对角化。应用修正后的估计退化模型就可以得到f 的估值=(C+ΔλI)-1g. 其中h =[h(0),h(1),…,h(M -1)]是点扩散函数,比较修正前后的循环矩阵可知,经过对角加载后的点扩散函数变为h' =[h(0)+Δλ,h(1),…,h(M-1)],设其频谱为H'(u). 加载后的滤波矩阵变为

微量加载量Δλ 的选取是自适应的过程,经多次仿真实验,取Δλ =1/L 可得到较好的复原效果,L为圆弧长度,所以越往图像边缘,加载量越小。
3.2.2 对角加载算法的改进——梯度加载算法
但是另一方面,对角加载会影响矩阵的小特征量,使得小特征量趋向等于加载量λ,导致高频分量加强,反映在图像上就是复原图像引起一定的震荡,导致抗噪能力降低。如果在保持低复杂度的情况下,引入新的加载,在修复病态性的同时,提高算法的抗噪能力和鲁棒性,将是一举两得的解决方案。在此实验过程中可以发现,由于退化函数模型的特殊性,在引入对角加载的过程中,将产生针对像素点的单向平滑效应。针对此特点,只需要再引入相应有方向性的简单约束,即可实现对图像的平滑,而梯度算子正是这样的一种方案。梯度加载C″ =C +Δλ·Δ,即由梯度矩阵取代原来的单位矩阵。前面分析,逆滤波是一种无约束的复原,对角加载只是改善了矩阵的病态性,并没有给任何约束,仍然是一种无约束的复原。在f(x)的一阶导数即梯度计梯度算子为 ,引入梯Δ度算子就相当于给简单的方向性约束,即可实现图像的平滑。
梯度矩阵为

即修正后的矩阵为

C″仍然是循环矩阵,比较可得,梯度算子加载后的点扩散函数变为

其频谱为H″(u),剃度加载后f 的估计值
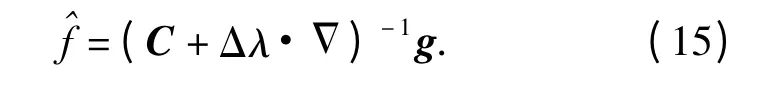
加载后的滤波矩阵变为

通过梯度加载量的引入,既可以避免图像复原的退化矩阵的病态性,又可以实现图像的平滑。相对极坐标变换法和约束最小二乘法,梯度加载算法的计算量大大减少,梯度加载复原只需要进行一次退化函数的傅里叶变换,可以用快速傅里叶变换算法计算,避免了前面算法的大量乘法运算和多次傅里叶变换计算。计算量的降低对于弹上系统等实时性要求很高的系统具有重大的意义。
不管是维纳滤波还是对角加载滤波复原,都是首先沿模糊路径快速提取模糊像素的灰度值g(i),然后在频域内进行滤波得到估计值的频谱(u),再快速傅里叶逆变换得到(i),这样从小到大改变半径,逐步恢复各模糊路径上的图像数据。由于模糊路径上的点不能全部映射直角坐标系下的像素点,所以恢复后的图像会出现空穴点(即未恢复的像素点),可以使用中值滤波或邻域求均值的方法消除空穴点。
4 实验结果及分析
4.1 复原效果评价指标
除了直观的视觉图像复原效果,本文采用峰值信噪比作为客观评价指标来评价图像复原前后的效果。峰值信噪比PSNR 定义为

式中:Ii分别表示清晰图像和复原图像的灰度值,M、N 为图像的长和宽。
4.2 极坐标下的图像复原过程
图2为基于极坐标变换(CRT)的图像复原过程,图2(a)为旋转角度10°的模糊图像,图2(b)为模糊图像在极坐标下的变换,图2(c)为复原后的清晰极坐标图像,图2(d)为清晰极坐标图像变换到直角坐标系下的图像,是最终的复原图像。由于作了两次的坐标变换和两次灰度插值,在离散的极坐标变换过程中,图像中心和图像边缘采用相同的量化步长,导致图像中心处信息冗余而图像边缘处信息丢失,越靠近边缘信息丢失越多,复原效果也就越差;在极坐标逆变换过程再次插值运算,导致信息进一步丢失,所以复原效果不佳,且有一定的振荡效应。复原图像的算法效果(峰值信噪比PSNR)见表1.

图2 基于CRT 的图像复原过程Fig.2 The restoration process of rotary motion-blurred image based on CRT

表1 算法效果(PSNR)比较Tab.1 The effects of different algorithms dB
4.3 基于模糊路径提取的图像复原效果
与CRT 算法不同,基于模糊路径的复原方法,是沿模糊路径由小到大逐个去除其空间可变模糊。为了证明算法在大角度旋转模糊条件下的适应性,在不同的旋转角度下进行基于模糊路径提取的维纳滤波仿真实验,表2为仿真图像复原效果,可见即使在旋转模糊角度较大的情况下,本文算法仍然得到较好的复原效果。这主要是因为采用了沿模糊路径的空间自适应算法,不同于CRT 算法使用相同的点扩散函数,算法根据不同的模糊路径长度采用不同的点扩散函数,因而能够较好地复原模糊路径较大时的旋转模糊图像。

表2 在不同旋转角度下基于模糊路径提取的复原效果图Tab.2 Comparison of blurred images and restored images at different rotary angle
噪声是影响图像复原效果的一个重要因素,为了证明本文算法的鲁棒性,模糊退化图像叠加不同信噪比高斯噪声进行仿真实验,模糊角度为10°,分别叠加40 dB、30 dB 和20 dB 的加性高斯噪声,复原效果如表3所示。在信噪比下降的情况下,复原图像的信噪比也逐渐下降,且图像边缘产生了一定的振铃效应,但仍然具有较好的复原效果。

表3 不同信噪比下的复原效果Tab.3 Restored results under different SNRs
按照(17)式计算各种算法复原图像的峰值信噪比PNSR,见表1.
极坐标变换的方法对图像的改善效果较差,复原图像的信噪比明显低于基于模糊路径提取的方法。维纳滤波由于引入平滑效应,复原图像的视觉效果好于对角加载,但其锐度较低,峰值信噪比不如对角加载和梯度加载;对角加载锐度较高,但是其高频加强的特性也使得噪声得到放大,且边缘处有震荡条纹,主要是直接引入对角加载无约束造成的;而引入约束的梯度加载复原图则明显地降低了震荡效应,且有较好的锐度和视觉效果,集合了维纳滤波和对角加载的优点。
4.4 算法处理时间比较
所有算法都在Intel 酷睿i3 3.1 GHZ,VC2005的环境下仿真,不同尺寸的图像使用不同算法的时间比较,如表4所示,算法处理时间随图像尺寸的增大呈指数级增长,基于模糊路径的方法(维纳滤波、对角加载和梯度加载方法)处理时间相差不大,但远小于传统的极坐标变换方法,且图像越大差距越明显。

表4 算法处理时间比较Tab.4 Processing time of different algorithms s
4.5 真实图像复原效果
为了验证算法的实际可行性,利用实验室架构的旋转模糊图像平台采集模糊图像,旋转平台的角速度ω 可调,且CCD 的曝光时间t 已知,相乘可得到曝光时间内图像的旋转角度,即模糊角度θ =ωt.如图3所示,图3(a)为实际CCD 采集的旋转模糊图像,图3(b)为其复原效果图。但实际图像的复原效果不如仿真效果,分析其原因,主要有两点:1)转台旋转时其旋转轴心并不完全稳定,因而模糊路径并不是模型中假设的标准圆;2)实际采集的图像有噪声的影响,且图像信噪比无法精确得知,影响了图像反卷积复原的效果。
5 结论

图3 实际模糊图像的复原效果图Fig.3 The restored results of real blurred images
本文对径向可变模糊图像复原问题进行了研究。不同于以往的CRT 方法,本文不需要进行坐标变换的繁琐运算,而是用最小偏差插补算法提取模糊路径上的像素灰度值。针对提取后的一维模糊像素值,提出了维纳滤波法、对角加载和梯度加载的方法。进行了仿真实验,验证了算法复原效果,有良好的抗噪能力;对实际采集的旋转模糊图像复原,也得到了较好的复原效果。
References)
[1] Sawchuk A A,Space variant image restoration by coordinate transformations[J].JOSA,1974,64(2):138 -144.
[2] Sawchuk A A.Space variant image motion degradation and restoration[J].Proceedings of IEEE,1972,60(7):854 -861.
[3] 洪汉玉.成像探测系统图像复原算法研究[D]. 武汉:华中科技大学,2004:122 -125.HONG Han-yu. Research on image restoration algorithms in imaging detection system[D]. Wuhan:Huazhong University of Science and Techonology,2004:122 -125. (in Chinese)
[4] 洪汉玉,张天序.非零边界旋转运动模糊图像的恢复算法[J].中国图像图形学报,2004,9(3):265 -274.HONG Han-yu,ZHANG Tian-xu. Restoration algorithm for rotational motion blurred images with non-zeros boundary[J]. Image and Graphics,2004,9(3):265 -274. (in Chinese)
[5] 赵巍.数控系统的插补算法及减速控制方法研究[D]. 天津:天津大学,2004:23 -31.ZHAO Wei.Research on interpolation algorithm and accelerationdeceleration controller in CNC system[D]. Tianjin:Tianjin University,2004:23 -31. (in Chinese)
[6] Wright W E. Parallelization of Bresenham’s line and circle algorithms[J]. Proceedings of IEEE Computer graphics and Applications,1990,9(6):60 -67.
[7] Heltrom C W. Image restoration by the method of least squares[J].JOSA,1967,57(3):297 -303.
[8] 邹谋炎. 反卷积和信号复原[M]. 北京:国防工业出版社,2001:91 -111.ZOU Mou-yan. Deconvolution and signal recovery[M]. Beijing:National Defense Industry Press,2001:91 -111. (in Chinese)
[9] 张杰,廖桂生,王珏. 对角加载对信号源数检测性能的改善[J].电子学报,2004,32(12):2094 -2097.ZHANG Jie,LIAO Gui-sheng,WANG Jue. Performance improvement of source number detection using diagonal loading[J]. Acta Electronica Sinica,2004,32(12):2094 -2097. (in Chinese)
