过载指令约束下的导弹导引律设计

孟克子，周荻

(哈尔滨工业大学 航天学院，黑龙江 哈尔滨150001)

0 引言

经典的比例导引律形式简单、易于实现，被广泛应用于引导导弹拦截非机动目标或弱机动目标且十分有效，但比例导引律用于拦截大机动目标时难以满足制导精度要求［1］。目前，许多非线性控制方法被用于新型导引律的设计，如几何控制方法［2］，Lyapunov函数方法［3］，非线性H∞控制方法［4］，一阶滑模控制方法［5-6］等。

在实际应用中，由于物理约束(主要是饱和约束)的存在，导引律产生的过载指令信号可能会受到限制，从而会降低制导性能甚至导致制导系统不稳定，尤其是导弹相对目标过载能力优势不大的情况，如空空导弹拦截无人机，无人机由于无人驾驶可执行较大的过载机动。目前，过载指令约束下的导引律设计主要采用最优控制方法［7-11］。Rusnak等［7-9］以零脱靶量和能量最优为性能指标，基于极小值原理推导了过载指令约束下的最优导引律。Hexner 等［10-11］针对导弹的过载指令饱和以及目标的随机机动特性，采用线性二次型高斯(LQG)理论和随机输入描述函数(RIDF)设计了过载指令约束下的最优导引律。需要说明的是，文献［7 -11］中采用的是以目标-导弹在参考直角坐标系中的纵向相对位置(或相对位置)及其导数作为主要状态变量的线性时不变制导方程。而通常采用在极坐标下建立的以目标-导弹相对距离及视线角速率为主要状态变量的制导方程依据准平行接近理论设计导引律更具实际意义。

Farrell 等［12］针对输入饱和的不确定非线性系统，提出了指令滤波backstepping 方法，能够有效消除饱和非线性的影响。Farrell 等［13］和Sonneveldt等［14］成功地将指令滤波backstepping 方法用于输入饱和的非线性飞行设计问题。指令滤波backstepping 方法通过引入指令滤波器和构造辅助微分方程来处理饱和约束，同时指令滤波器避免了传统backstepping方法中由于对虚拟控制的解析求导而出现的“项数爆炸”现象。

另外，导弹自动驾驶仪动态特性是影响制导精度的主要因素之一。Chwa 等［15］采用滑模控制设计了考虑导弹控制回路动态特性的自适应非线性导引律。考虑导弹自动驾驶仪的一阶动态特性，孙胜等［16］利用backstepping 方法设计了三维非线性导引律。曲萍萍等［17-18］采用动态面控制法设计了考虑导弹自动驾驶仪二阶动态特性的平面及三维非线性导引律。

鉴于指令滤波backstepping 方法的优点及导弹自动驾驶仪动态特性对制导精度的影响，本文基于以目标-导弹相对距离和视线角速率为主要状态变量的平面制导方程，采用指令滤波backstepping 方法在导弹自动驾驶仪存在二阶动态延迟的情况下设计了一种过载指令约束下的导引律，并针对视线方向施加控制和不施加控制两种情况进行了仿真验证。

1 问题描述

平面内目标-导弹相对运动几何关系如图1所示，其中M 和T 分别表示导弹和目标的质心，R 表示目标-导弹之间的相对距离，q 表示视线角，vm和vt分别表示导弹和目标的速度，θm和θt分别表示导弹和目标的弹道倾角。

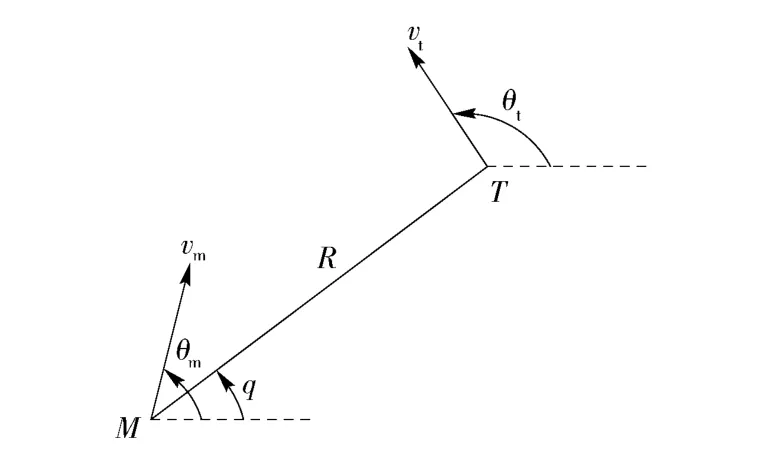
图1 平面内目标-导弹相对运动几何关系Fig.1 Relative kinematic relationship between target and missile in the plane

由图1可导出目标-导弹相对运动学方程为

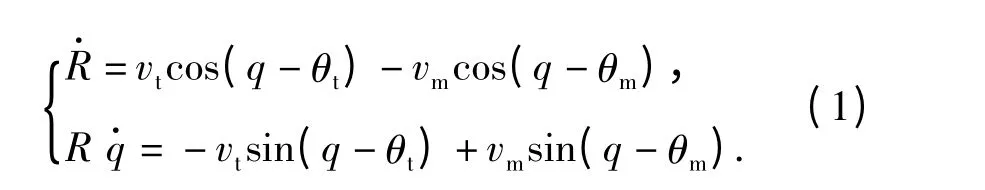
(1)式相对时间t 求导并整理，可得

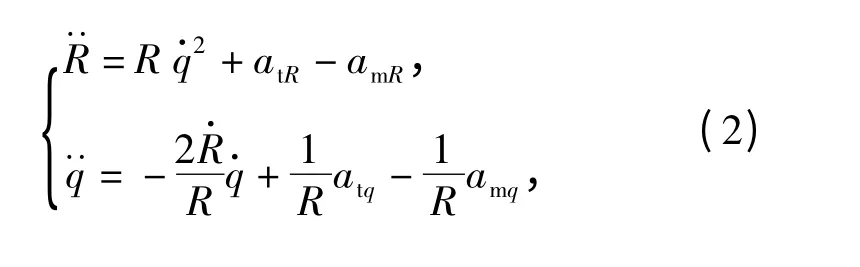
式中:atR和atq分别表示目标加速度沿视线方向和视线法向的分量;amR和amq分别表示导弹加速度沿视线方向和视线法向的分量。

过载指令约束下的导弹自动驾驶仪二阶动态特性为

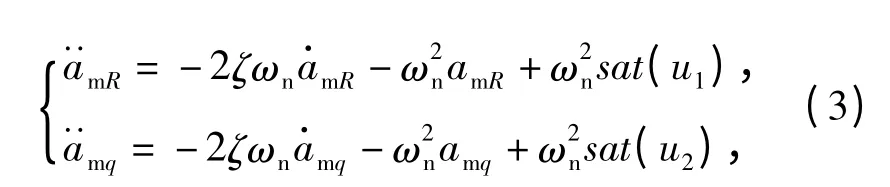
式中:

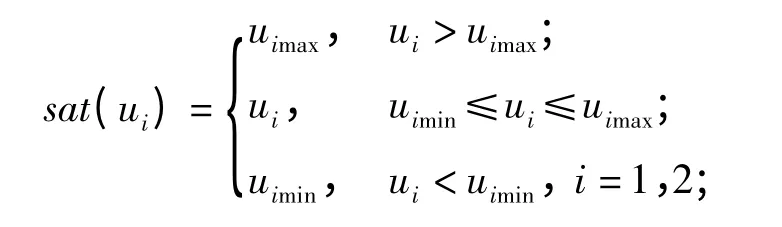
ζ 和ωn分别表示自动驾驶仪二阶动态特性的阻尼比和自然振荡角频率;u1和u2分别表示视线方向和视线法向的导弹自动驾驶仪过载指令。

设末制导的初始时刻为0，结束时刻为tf. 为了拦截目标，期望tf时刻R 变为0. 而R 变为0 的充分条件是目标-导弹相对速度满足(4)式所示的约束关系。文献［6，19］采用变结构控制设计了视线方向的导引律u1. 而文献［20 -21］认为渐近稳定并非R 的理想响应特性，其以局部稳定原则设计了不以R 渐近稳定为目标的视线方向导引律u1，且制导性能更高。由此，本文在假设推力可控的条件下依循文献［20 -21］的思路设计u1.

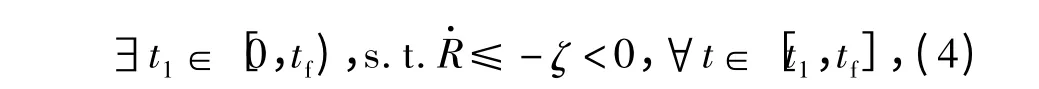
式中:ζ=const ＞0.

x1-子系统:

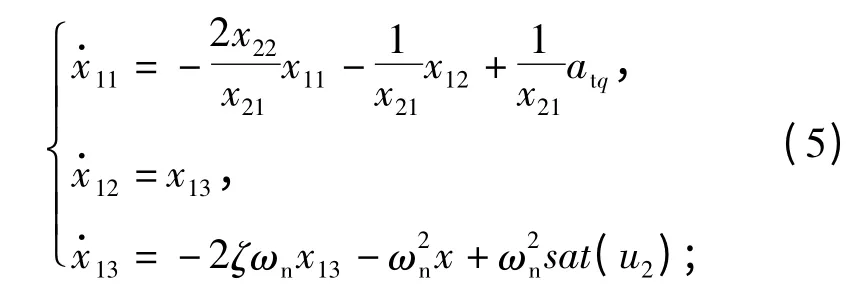
x2-子系统:

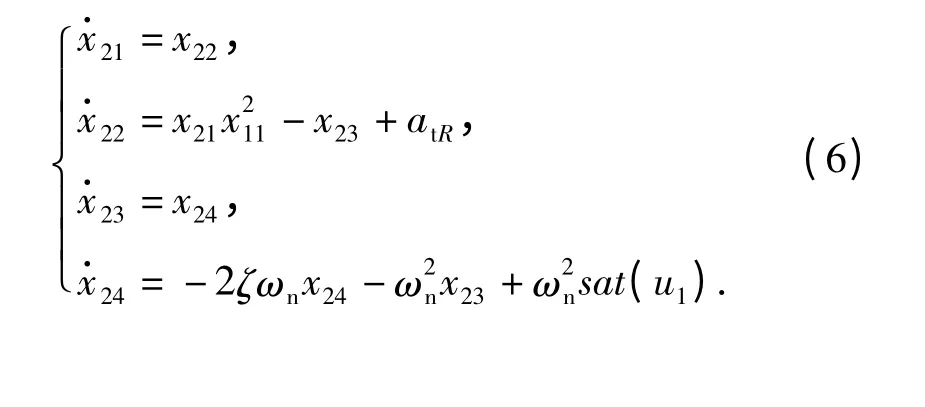
通常目标加速度难以测量，但其一定是有界的，在导引律的设计过程中将其视为有界干扰，满足|atq| ＜ε1和|atR| ＜ε2，其中ε1、ε2(可根据对目标加速度的估计而定)为已知的正常数。

2 视线法向导引律设计及稳定性分析

2.1 指令滤波器

指令滤波器［15-17］的方框图如图2所示，x0d为滤波前的虚拟/名义控制指令。滤波器状态空间形式为

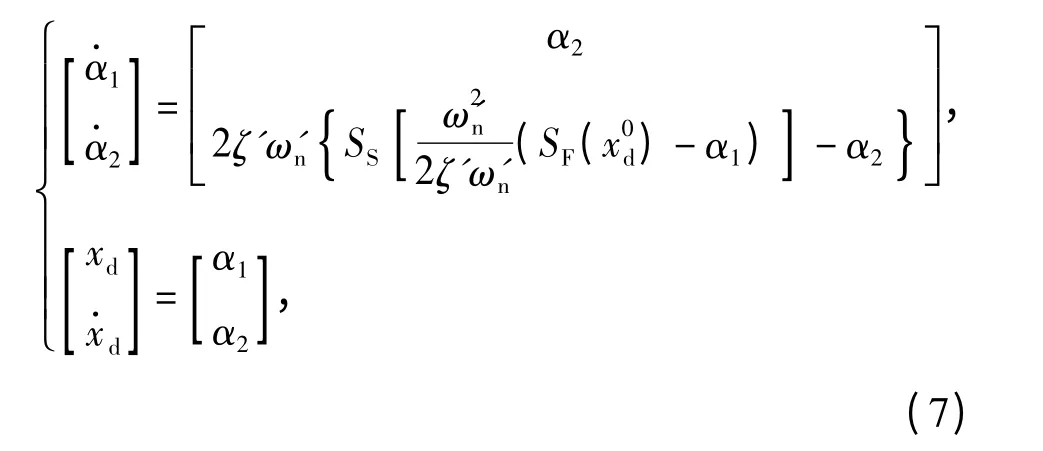
式中:SF(·)和SS(·)分别为对应于幅值与速率的饱和函数，SF(·)与SS(·)的定义类似，表示为

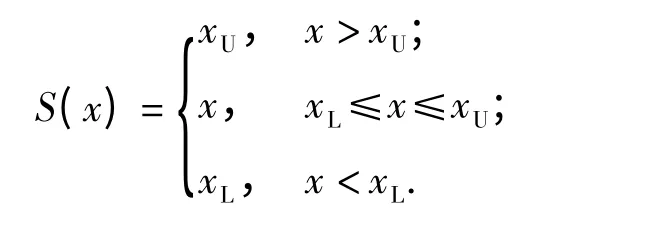
式中:xU和xL分别为变量x 的上限和下限。

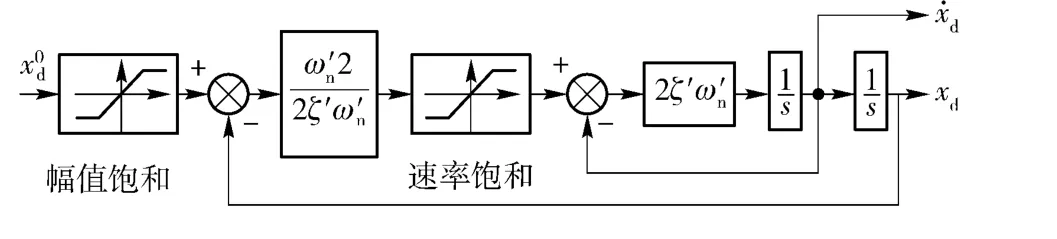
图2 指令滤波器Fig.2 Command filter

指令滤波器的功能:1)计算虚拟控制xd及其对时间的导数，消除了传统backstepping 方法中虚拟控制的解析求导运算;2)保证虚拟控制xd及其对时间的导数满足约束。如果采用指令滤波器只是为了计算xd及其导数，那么xU应取为正无穷大，xL应取为负无穷大，此时指令约束不起作用。指令滤波器转化为

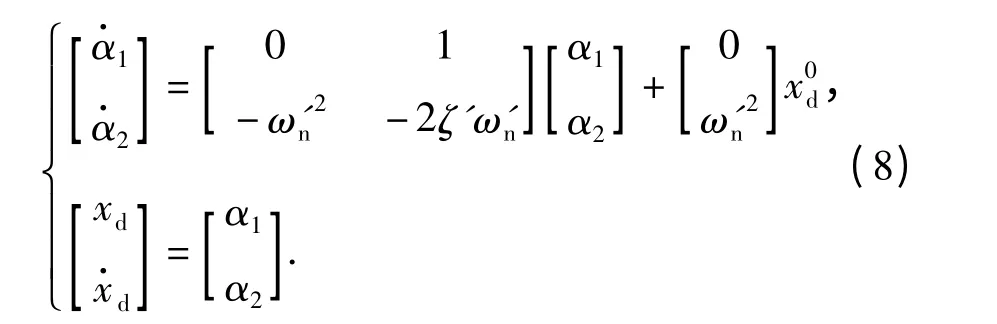
注意到，如果x0d有界，则xd和有界且连续。则误差xd-x0d总是有界的。当指令信号不存在约束时，可以通过选取比x0d的带宽大的多的ω'n使得误差xd-x0d为任意小。

2.2 视线法向导引律设计

定义跟踪误差

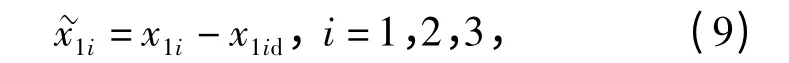
式中:x11d=0 为视线角速率的期望值，x1id(i =2，3)将在下文中定义。

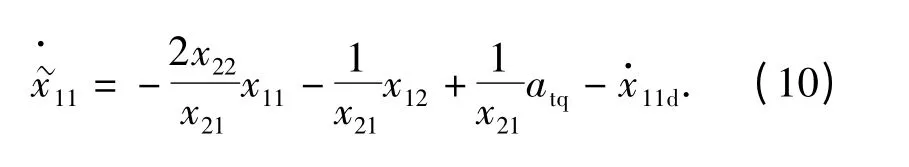
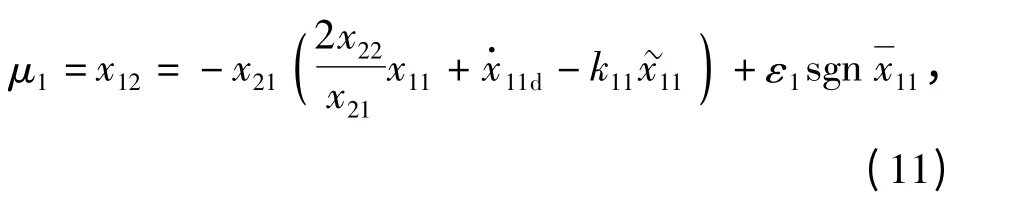
式中:k11=constant ＞0;为跟踪误差的修正项，将在下文中定义。

基于指令滤波backstepping 方法，过载指令约束下的视线法向导引律的设计步骤如下:

1)定义

式中:ζ12将在下文中定义。虚拟控制经过指令滤波器产生幅值、速率和带宽约束的虚拟控制x12d及其对时间的导数定义辅助微分方程

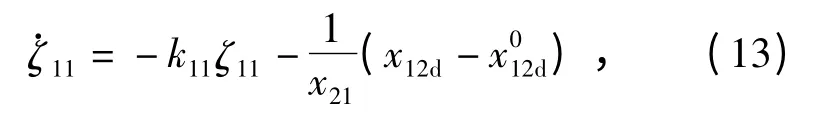
(13)式为构造的线性稳定的辅助微分方程，ζ11表征了约束对跟踪误差的影响，下文中的ζ12、ζ13、ζ23、ζ24与ζ11意义类似。

2)定义修正跟踪误差

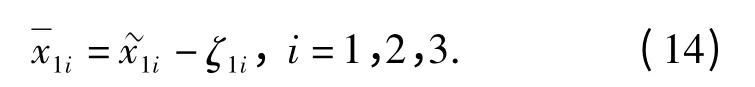
3)定义

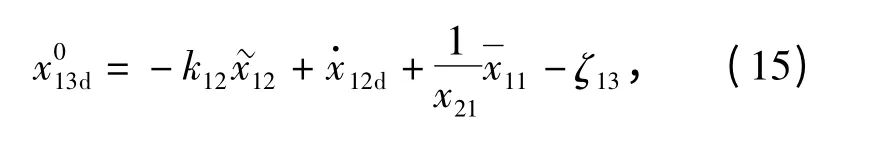
式中:k12=constant ＞0;ζ13将在下文中定义。虚拟控制经过指令滤波器产生带约束的虚拟控制x13d及其对时间的导数定义辅助微分方程

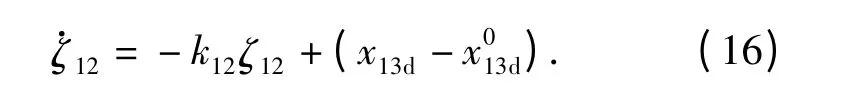
4)定义名义控制

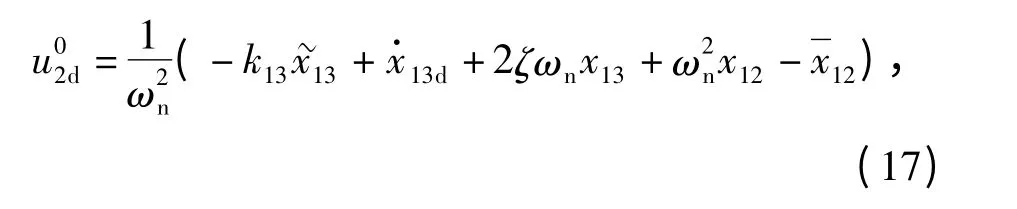
式中:k13=constant ＞0. 名义控制经过指令滤波器产生带约束的控制u2d. 定义辅助微分方程

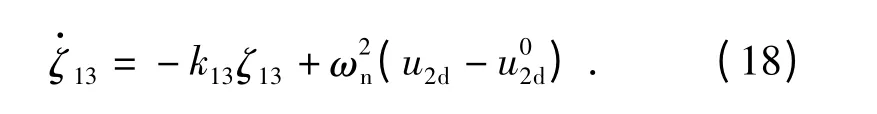
在指令滤波器的作用下，u2d位于饱和界限范围之内，是物理上可执行的。由此，认为

需要说明的是，指令滤波backstepping 视线法向导引律并非全解析表达式，而是中间表达式(12)式、(15)式、(17)式，辅助微分方程(13)式、(16)式、(18)式以及指令滤波器的组合，其实现过程如图3所示。制导律中含有的微分方程为低阶线性方程，只需用4 阶龙格-库塔法进行简单的数值积分运算，我们在普通的计算机上用Matlab 编程实现该制导算法时，解算出一拍的制导指令只需要10 ms. 考虑到现代计算机的快速解算能力，该导引律在弹上用数字信号处理器实现并不困难。

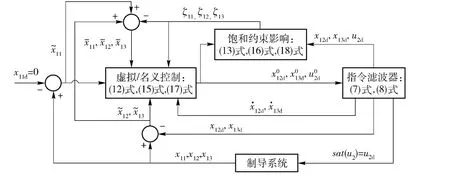
图3 指令滤波backstepping 视线法向导引律结构框图Fig.3 Block diagram of guidance law along the normal direction of LOS based on command filtered backstepping

2.3 基于Lyapunov 函数的x1-子系统稳定性分析

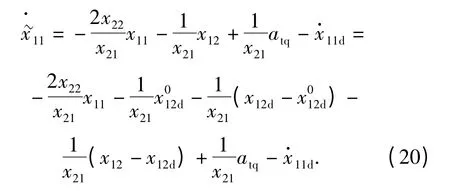
结合定义(9)式和(14)式，分别将(11)式～(13)式代入(20)式中，得

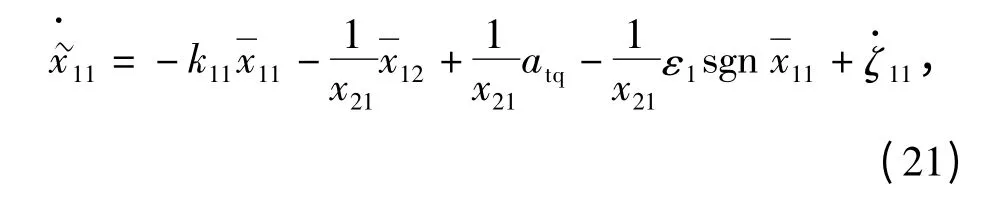
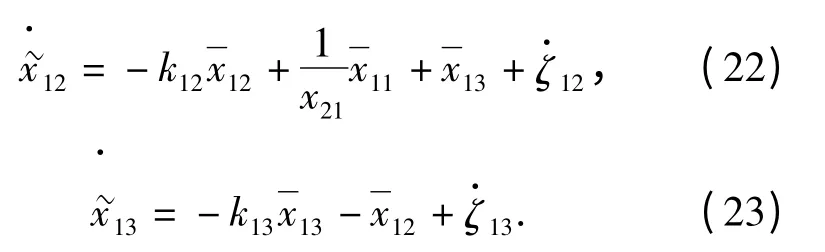
结合定义(14)式和(21)式～(23)式，可得修正跟踪误差(i=1，2，3)的动态为

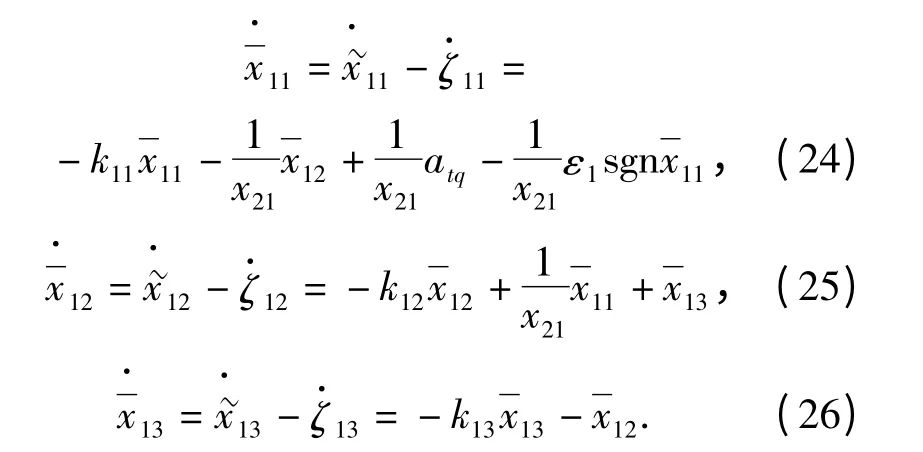
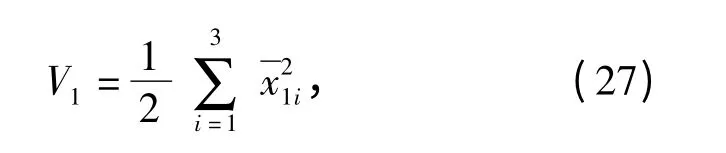
(27)式对时间t 求导并将(24)式～(26)式代入，得

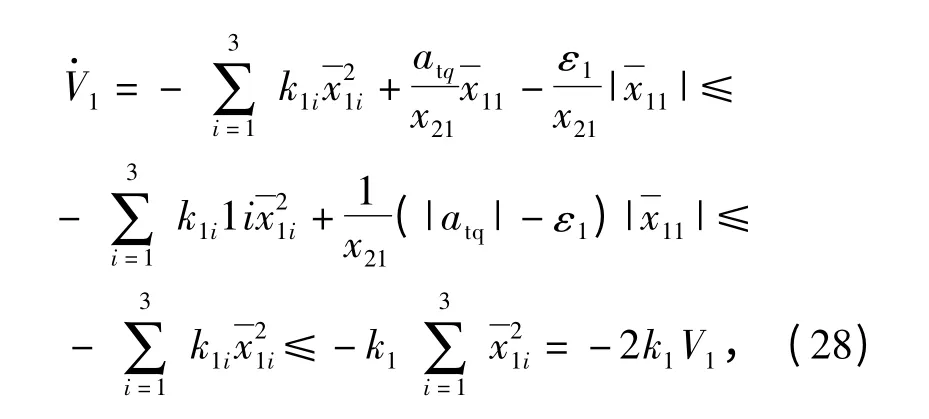
式中:k1=min{k1i，i=1，2，3}. 求解(28)式，得

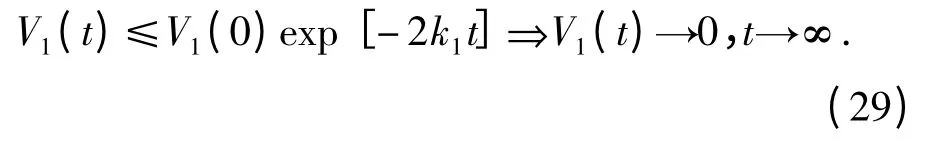
由(29)式可知，无论控制及中间虚拟控制是否饱和，修正跟踪误差(i =1，2，3)都将随着时间t趋于无穷大而趋于0，而实际跟踪误差(i =1，2，3)无此性质。但是，文中只考虑名义控制的饱和非线性，中间虚拟控制状态(i=2，3)不存在饱和约束，亦即2.2 节中1 步和3 步中采用的是(8)式所示的指令滤波器，而4 步中采用的是(7)式所示的指令滤波器且只约束幅值。由此，误差u2d-非0但有界，而误差x1id-x01id(i=2，3)在(8)式所示的滤波器作用下可为任意小。则变量ζ13非0 但有界而变量ζ11和ζ12将趋近于0. 零化ζ11使得修正跟踪误差11趋于实际跟踪误差由此，视线角速率q·渐近趋近于0，满足视线法向导引律u2的设计目标。

3 视线方向导引律设计及稳定性分析

若导弹在制导过程中，推力不可控或推力为0，则(4)式要依靠制导过程初始时刻目标-导弹相对运动几何关系保证。若导弹在制导过程中，推力大小和方向可控，为使满足(4)式所示的约束，则可以按如下步骤设计视线方向导引律u1.

3.1 视线方向导引律设计

选取虚拟控制

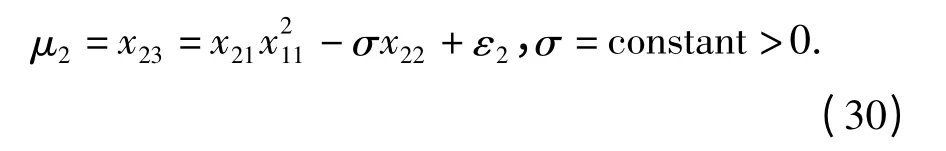
在虚拟控制μ2的作用下，有

求解(31)式，得

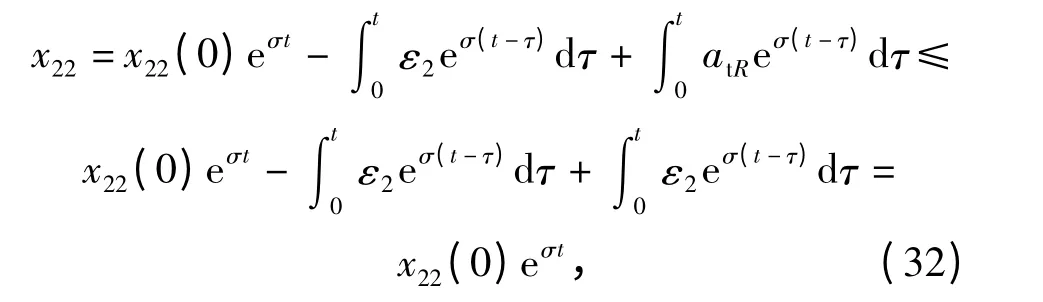
式中:x22(0)=(0). 选取(0)= -ζ，则对∀t∈［0，tf)，有=x22≤-ζ ＜0，满足(4)式所示的约束关系。

视线方向上导引律的设计目标转化为:在u1的控制作用下，使x23跟踪μ2的变化，从而使目标-导弹相对速度满足(4)式所示的约束关系。记

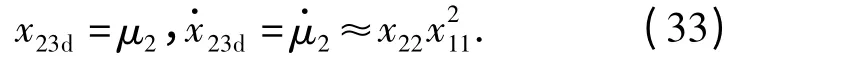
定义跟踪误差

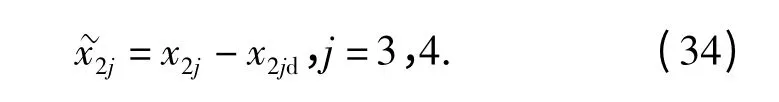
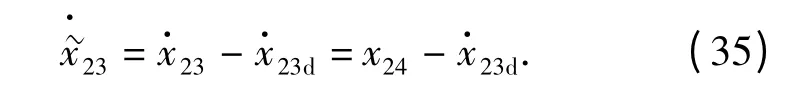
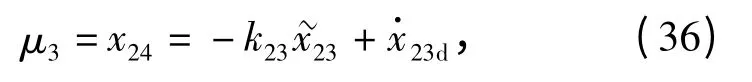
式中:k23=constant ＞0.

基于指令滤波backstepping 方法，过载指令约束下的视线方向导引律的设计步骤如下:1)定义

式中:ζ24将在第3 步中定义。虚拟控制经过指令滤波器产生带约束的虚拟控制x24d及其对时间的导数. 定义辅助微分方程

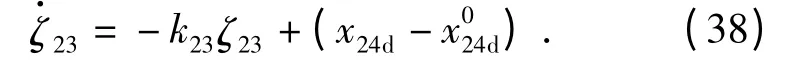
2)定义修正跟踪误差

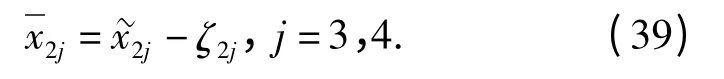
3)定义名义控制

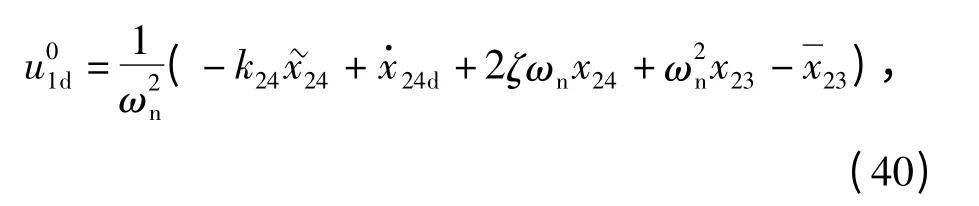
式中:k24=constant ＞0. 名义控制经过指令滤波器产生带约束的控制u1d. 定义辅助微分方程

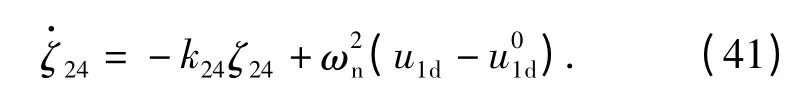
在指令滤波器的作用下，u1d位于饱和界限范围之内，亦即是物理上可执行的。由此，认为

与视线法向导引律相同，视线方向导引律也非全解析的形式，其实现的结构框图与图3类似，这里不再给出。

3.2 基于Lyapunov 函数的x2-子系统稳定性分析

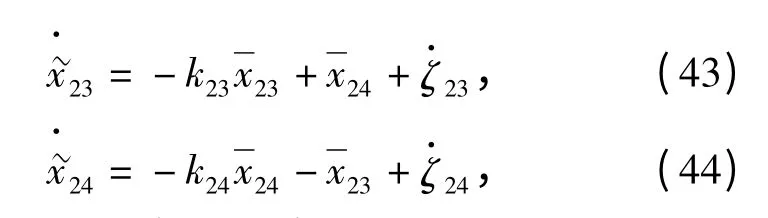
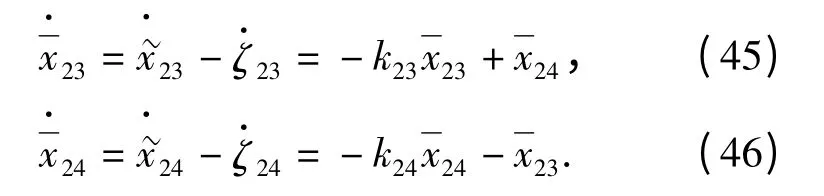
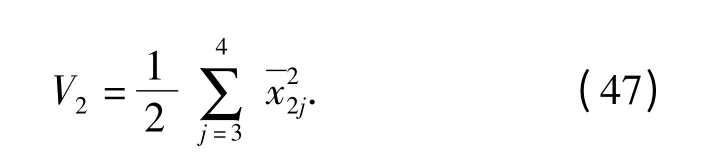
(47)式对时间t 求导并将(45)式和(46)式代入，得

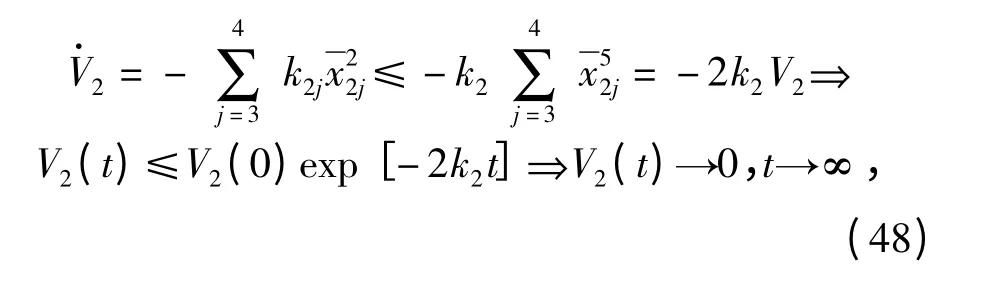
式中:k2=min{k2j，j=3，4}.

设计的导引律中所需的变量视线角及视线角速率、目标-导弹相对距离及其相对时间的导数以及导弹的加速度可以通过测量获得，导弹的加速度可以依据加速度的测量值通过滤波器估计获取。

对于指令滤波backsteppping 而言，为了保证Lyapunov 稳定性，只要求k1i(i=1，2，3)和k2j(j =3，4)大于0，而通常选择k11＜k12＜k13，k23＜k24以获得更好的响应特性。根据文献［10 -11］中指令滤波器参数的选取规则，阻尼比取为ζ' =1 且选取ω'n时保证下一步指令滤波器中的ω'n大于上一步指令滤波器的ω'n.

4 仿真验证

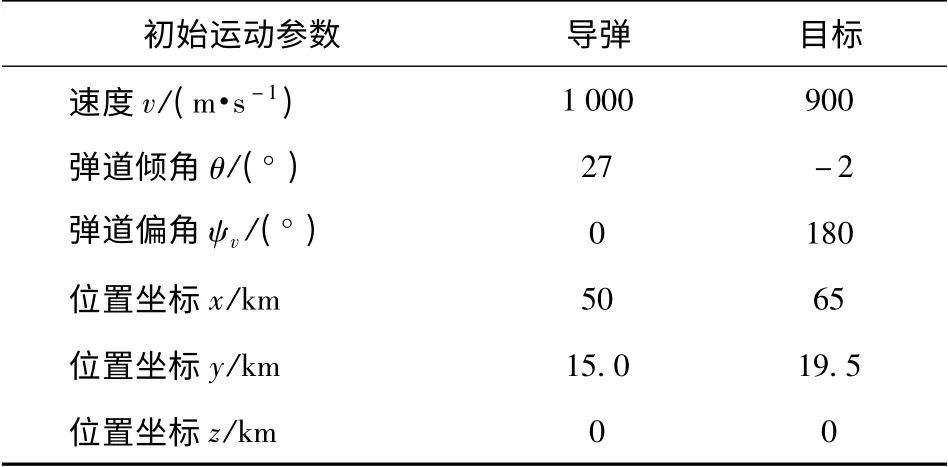
表1 导弹与目标初始运动参数Tab.1 The initial motion parameters of missile and target

4.1 视线方向施加控制作用

视线方向施加控制作用时，将设计的视线法向导引律和视线方向导引律综合记为NG1，相关参数εi=90(i =1，2)，k11=0.2，k12=0.4，k13=2，k23=3.37，k24=5.43，σ =0.05. 指令滤波器参数如表2所示。为了进行比较，引入局部滑模导引律［18］(PSMG):

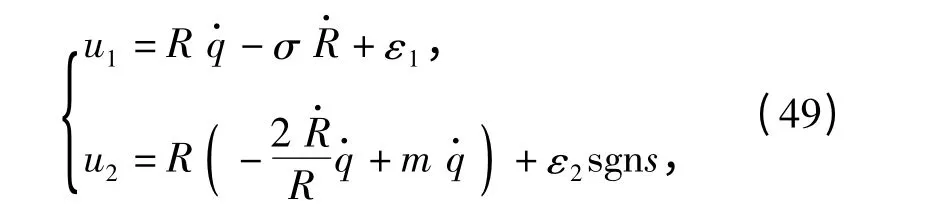
表2 指令滤波器参数Tab.2 Parameters of command filter

视线方向施加控制作用时的数值仿真结果如图4～图7所示。从图4和图5可以看出，无论是PSMG 还是NG1，可实施的过载指令信号都受到了一定程度的饱和约束;由于在设计NG1 的过程中对饱和约束进行了处理，所以视线角速率在约5.1 s 时收敛至0 附近的微小邻域内且直至最后一刻才发散，而PSMG 在设计过程中未对饱和约束进行处理且未考虑自动驾驶仪的动态特性，其视线角速率发散较早，如图6所示。最终，PSMG的脱靶量为9.85 m而NG1 的脱靶量只有0.05 m.由于两种情况下沿视线方向的控制作用基本相同(如图4所示)，以致导弹接近目标的速度几乎相等(如图7所示)，最终二者的拦截时间基本相当，PSMG 的拦截时间为7.70 s，NG1 的拦截时间为7.71 s.

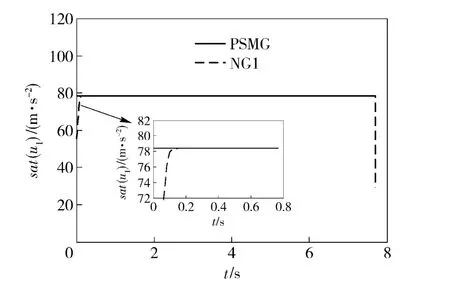
图4 视线方向施加控制时视线方向过载指令Fig.4 Acceleration command along LOS for controlling along LOS

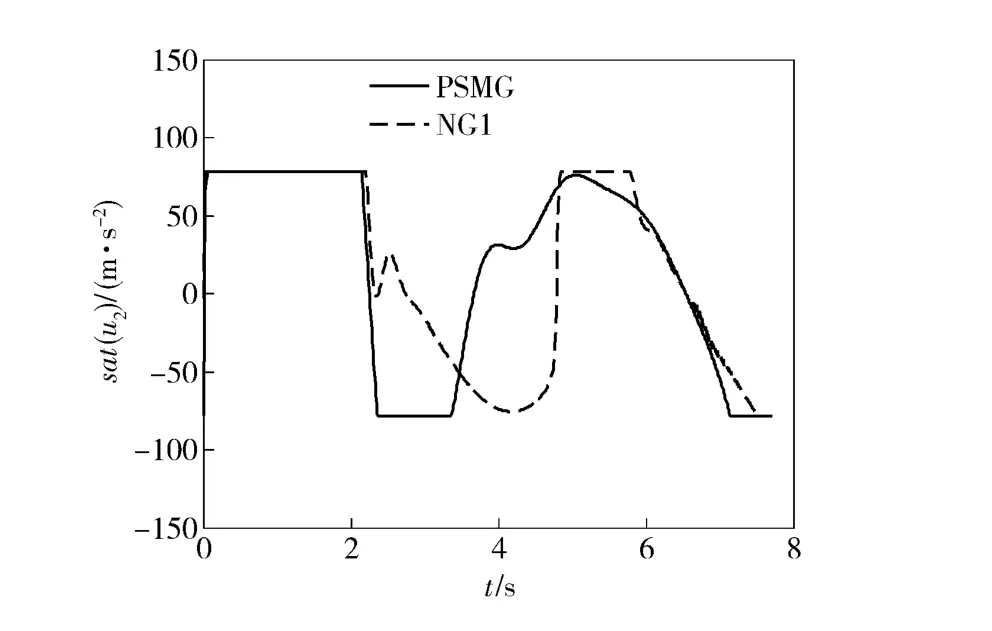
图5 视线方向施加控制时视线法向过载指令Fig.5 Acceleration command along the normal direction of LOS for controlling along LOS

图6 视线方向施加控制时的视线角速率Fig.6 LOS angular rate for controling along LOS

4.2 视线方向不可控

视线方向不施加控制时，只考虑视线法向导引律，记为NG2，相关参数与视线方向施加控制的情况相同。同样为了比较分析，引入增广比例导引律(APN):

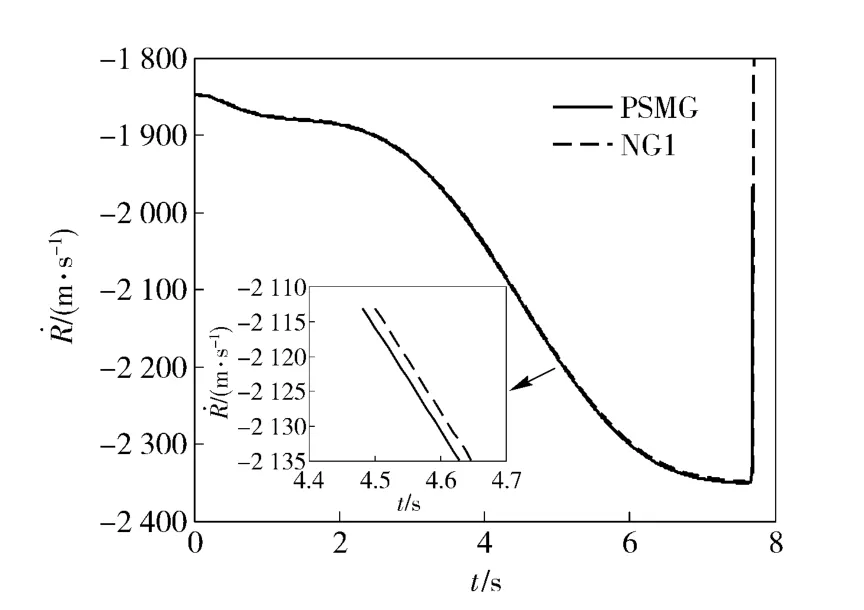
图7 视线方向施加控制时目标-导弹相对速度Fig.7 Relative velocity between target and missile for controlling along LOS

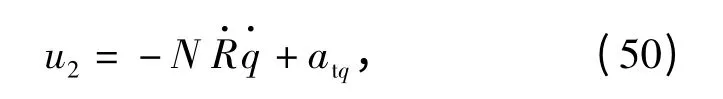
式中:N=3.4，假设目标加速度atq准确已知。

视线方向不施加控制时的数值仿真结果如图8～图10所示。在APN 和NG2 产生的过载指令都存在饱和现象的情况下，APN 的脱靶量为2.3 m而NG2 的脱靶量只有0.13 m. 同时，两种情况下视线方向都未施加控制作用，导弹-目标接近速度基本相当，最终拦截时间都是8.66 s.

最后，对比NG1 和NG2 的结果可知，视线方向施加控制作用能够使导弹以更快的速度接近目标，拦截时间更短。需要强调的是，以往对PSMG 和APN 的理论分析都是在不考虑过载指令约束的情况下做出的，当然性能良好。而将其应用于过载指令受限的情况下出现了正、负饱和现象，导致脱靶量下降。

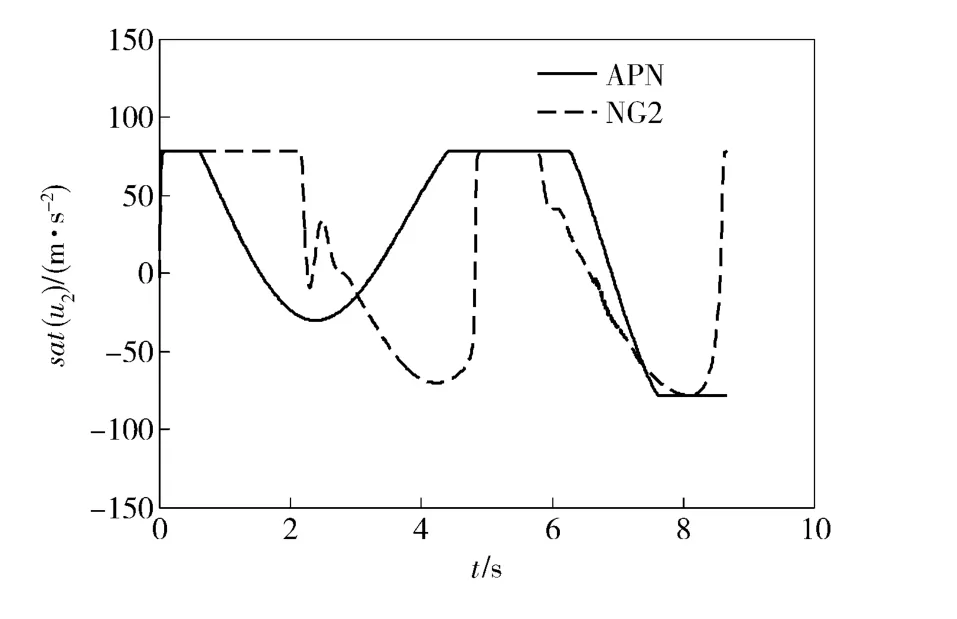
图8 视线方向不可控时视线法向过载指令Fig.8 Acceleration command along the normal direction of LOS for uncontrolling along LOS

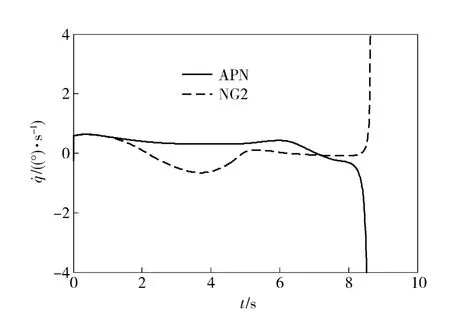
图9 视线方向不可控时的视线角速率Fig.9 LOS angular rate for uncontrolling along LOS

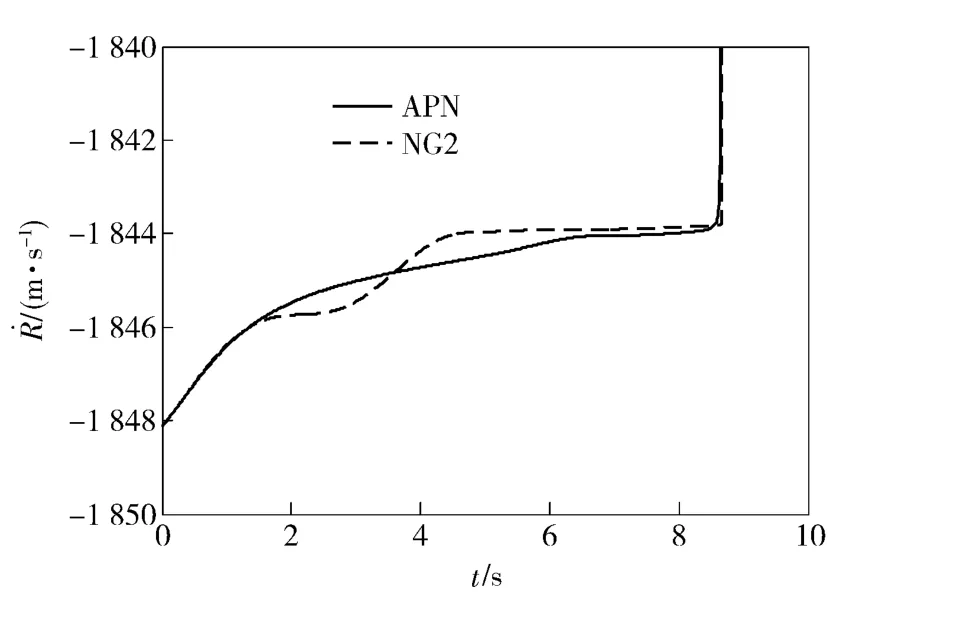
图10 视线方向不可控时目标-导弹相对速度Fig.10 Relative velocity between target and missile for uncontrolling along LOS

5 结论

考虑到导弹过载指令的饱和非线性以及导弹自动驾驶仪的动态延迟特性，基于平面目标-导弹相对运动方程，以“零化视线角速率”及“目标-导弹相对速度应小于一个负常数”为原则，采用指令滤波backstepping 方法设计了平面拦截导引律，指令滤波器不仅起到约束制导指令幅值的作用而且避免了传统backstepping 方法中“项数爆炸”的现象。研究结果表明，设计的导引律在过载指令饱和时仍能保证制导系统稳定且具有较高的制导精度。

References)

［1］ Zarchan P. Tactical and strategic missile guidance［M］. 3rd ed.Washington:American Institute of Aeronautics and Astronautics，1997.

［2］ Bezick S，Rusnak I，Gray W S. Guidance of a homing missile via nonlinear geometric control methods［J］. Journal of Guidance，Control，and Dynamics，1995，18(3):441 -448.

［3］ Song S H，Ha I J. A Lyapunov-like approach to performance analysis of 3-dimensional pure PNG laws［J］. IEEE Transactions on Aerospace and Electric Systems，1994，30(1):238 -247.

［4］ Yang C D，Chen H Y. Nonlinear robust guidance law for homing missiles［J］. Journal of Guidance，Control，and Dynamics，1998，21(6):882 -890.

［5］ Zhou D，Mu C D，Xu W L. Adaptive sliding-mode guidance of a homing missile［J］. Journal of Guidance，Control，and Dynamics，1999，22(4):589 -584.

［6］ Moon J，Kim K，Kim Y. Design of missile guidance law via variable structure control［J］. Journal of Guidance，Control，and Dynamics，2001，24 (4):659 -664.

［7］ Rusnak I，Meir L. Optimal guidance for acceleration constrained missile and maneuvering target［J］. IEEE Transactions on Aerospace and Electronic Systems，1990，26(4):618 -624.

［8］ Rusnak I，Meir L. Optimal guidance for high order and acceleration constrained missile［J］. Journal of Guidance，Control，and Dynamics，1991，14(3):589 -596.

［9］ Rusnak I. Advanced guidance laws for acceleration constrained missile，randomly maneuvering target and noisy measurements［J］. IEEE Transactions on Aerospace and Electronic Systems，1996，32(1):456 -464.

［10］ Hexner G，Shima T，Weiss H. LQG guidance law with bounded acceleration command［J］. IEEE Transactions on Aerospace and Electronic System，2008，44(1):77 -86.

［11］ Hexner G，Pila A. W. Practical stochastic optimal guidance law for bounded acceleration missiles［J］. Journal of Guidance，Control，and Dynamics，2011，34(2):437 -445.

［12］ Farrell J，Polycarpou M，Sharma M. On-line approximation based control of uncertain nonlinear systems［C］∥Proceeding of the 2004 American Control Conference. Boston，Massachusetts:IEEE，2004:2557 -2562.

［13］ Farrell J，Sharma M，Polycarpou M. Backstepping-based flight control with adaptive function approximation［J］. Journal of Guidance，Control and Dynamics，2005，28(6):1089 -1101.

［14］ Sonneveldt L，Chu Q P，Mulder J A. Nonlinear flight control design using constrained adaptive backstepping［J］. Journal of Guidance，Control and Dynamics，2007，30(2):322 -336.

［15］ Chwa D，Choi J Y. Adaptive nonlinear guidance law considering control loop dynamics［J］. IEEE Transactions on Aerospace and Electronics Systems，2003，39(4):1134 -1143.

［16］ 孙胜，周荻. 考虑导弹自动驾驶仪动特性的三维非线性导引律［J］. 宇航学报，2009，30(3):1052 -1056.SUN Sheng，ZHOU Di. Three-dimensional nonlinear guidance law with consideration of autopilot dynamics［J］. Journal of Astronautics，2009，30(3):1052 -1056. (in Chinese)

［17］ 曲萍萍，周荻. 考虑导弹自动驾驶仪二阶动态特性的导引律［J］. 系统工程与电子技术，2011，33(10):2263 - 2267.QU Ping-ping，ZHOU Di. Guidance law incorporating secondorder dynamics of missile autopilot［J］. Systems Engineering and Electronics，2011，33(10):2263 -2267. (in Chinese)

［18］ 曲萍萍，周荻. 考虑导弹自动驾驶仪二阶动态特性的三维导引律［J］. 航空学报，2011，32(11):2096 -2104.QU Ping-ping，ZHOU Di. Three-dimensional guidance law account for second-order dynamics of missile autopilot［J］. Acta Aeronautica et Astronautica Sinica，2011，32(11):2096 -2104. (in Chinese)

［19］ Liaw D C，Liang Y W，Cheng C C. Nonlinear control for missile terminal guidance［J］. Journal of Dynamic Systems，Measurement，and Control，2000，122:663 -668.

［20］ Shafiei M H，Binazadeh T. Partial stabilization-based guidance［J］. ISA Transactions，2012，51(4):141 -145.

［21］ Shafiei M H，Binazadeh T. Application of partial sliding mode in guidance problem［J］. ISA Transactions，2013，52(2):192 -197.