一种3自由度并联拟人机械腿的动力学建模及伺服电机峰值力矩预估

李研彪，李景敏，计时鸣，郑超，赵章风

(浙江工业大学 机械工程学院，浙江 杭州310014)

0 引言

目前，多数机械腿采用串联机构，具有结构复杂、承载能力小、运动惯性大等不足之处［1］，如日本早稻田大学研制的WL 系列双足拟人机器人，其双腿均采用串联机构，各腿具有5 个自由度。另外，日本本田公司、美国Sarcos 研究公司、德国Karlsruhe大学和北京航空航天大学等国内外机器人研究机构也相继研制出多种串联结构的仿生机械腿。相对串联机构，并联机构具有结构紧凑、承载能力大等优点［2］。本文对一种并联拟人机械腿的动力学模型及伺服电机峰值力矩预估进行了研究，其机构原型采用并联机构，如图1(a)所示。这种拟人机械腿通过3 个电机驱动，实现膝关节和踝关节的运动，类似于人体膝关节和踝关节的结构特点。其驱动装置安放在固定件的位置上，该机构的运动杆件不必承载驱动电机的重量，减少了电机数量，这种拟人机械腿具有结构简单、承载能力强、运动惯性小、运动灵活等优点，避免了传动系统复杂、动态特性差等缺点［1，3］。这种拟人机械腿与髋关节(髋关节机构原型为具有2 转动自由度的球面并联机构)串联在一起，构成了拟人下肢机器人，如图1(b)和图1(c)所示。

动力学研究的是物体的运动和作用力之间的关系。机器人的动力学模型用于描绘机器人这种复杂动力系统，以处理其动力响应、动力仿真和计算控制等［4］。目前研究机器人系统动力学的方法很多，有拉格朗日方法［5-11］、牛顿-欧拉方法、高斯方法、凯恩方法、旋量(对偶数)方法［12］、罗伯逊-魏登堡方法和影响系数方法等，其中拉格朗日方法和牛顿-欧拉方法运用较多。拉格朗日方法不仅能以最简单的形式求得非常复杂的系统动力学方程，而且具有显式结构。牛顿-欧拉方法则是基于运动坐标系和达朗贝尔原理建立起来的，没有多余信息，计算速度快。从事这方面理论研究的学者比较具代表性的有Lee 等［13］、Cheroutre-Vialette 等［14］和Miller 等［15］。目前，对机构的驱动端伺服电机峰值力预估的研究已经取得一些研究成果，为本研究的实施奠定了基础［16-19］。本文在运动学基础上采用拉格朗日方法对该并联机械腿进行动力学分析，并在动力学模型的基础上对驱动端伺服电机模型进行预估，得到了该机械腿的动力学特性。机械腿的研究是步行机器人研究的核心内容，其性能决定了整个机器人的性能。所以该机械腿的研究为这种并联拟人机械腿的应用奠定了理论基础。

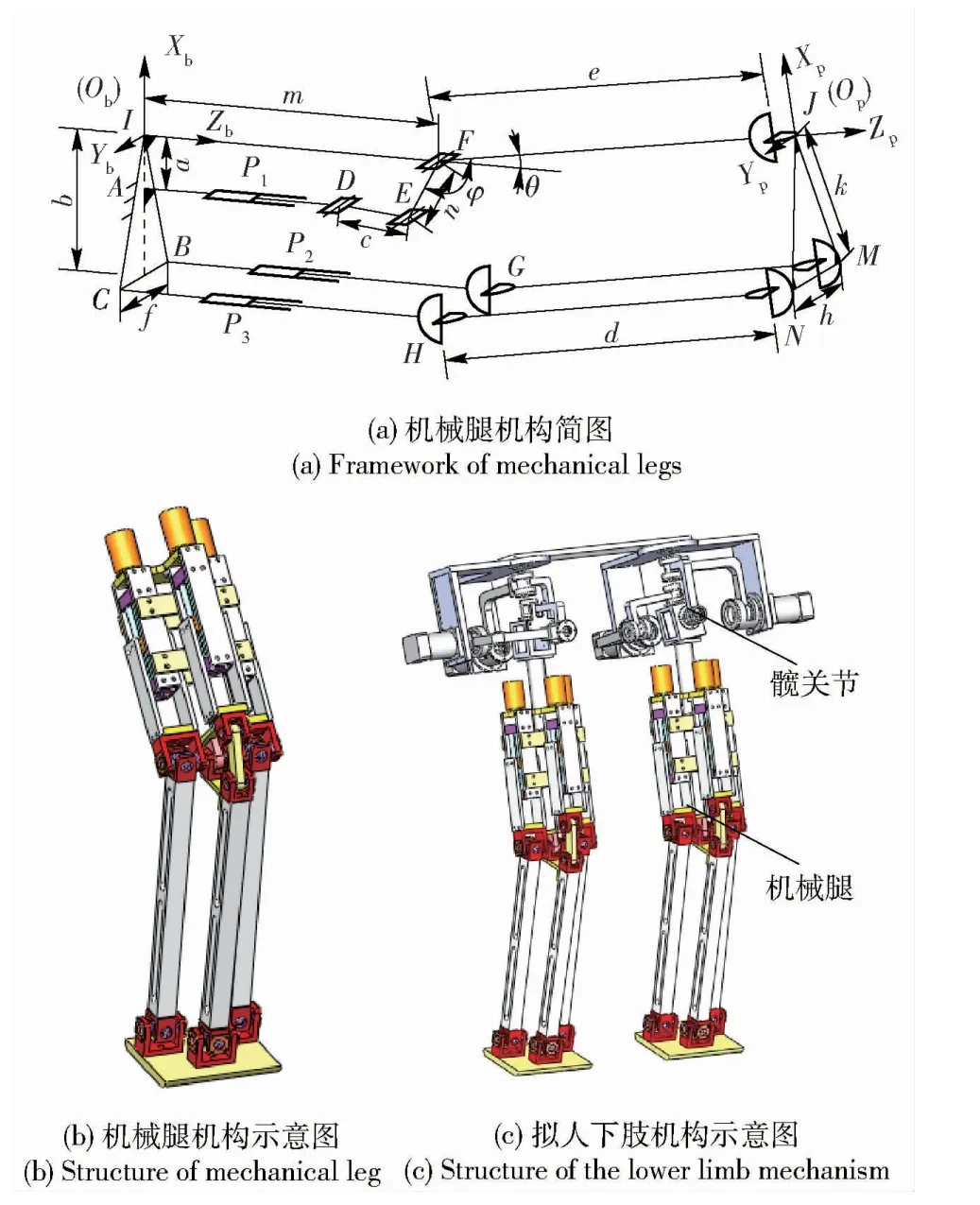
图1 拟人下肢机器人Fig.1 Mechanical legs

1 机构简述

这种拟人机械腿机构以一种3 自由度并联机构为机构原型，如图1(a)所示。该机械腿机构采用2PUU(移动副-胡克铰-胡克铰)/PRRRU(移动副-转到副-转到副-转到副-胡克铰)的结构形式，动平台通过2 条相同的支链PUU 和一条支链PRRRU 与静平台相连。其结构布局特点如下:

1)3 个直线移动副P1、P2和P3相互平行且均安装在基座上。

2)当杆FJ 与杆IF 共线，面JMN 垂直于杆FJ时，各移动副输入均为0，这种状态为此机构的初始位姿。此时，移动副P1、P2、和P3的初始长度为li，i=1，2，3，Δli为直线移动副P1、P2、和P3的输入位移。根据这种机构的结构特点可知:该机械腿可绕点F 转动以实现膝关节运动，可绕J 点的Xp轴和Yp轴转动来实现踝关节的运动。建立2 个坐标系{B}:ObXbYbZb和{P}:OpXpYpZp，其中坐标系{B}为基坐标系，坐标系{P}为动坐标系。

2 运动反解

设:v=(vxvyvz)T为动平台上的参考点Op在基坐标系{B}(以下无特殊说明均表示在该坐标系下定义)中的速度矢量;ω=(ωxωyωz)T为动平台的角速度矢量;vi分别为移动副Pi，i =1，2，3的输入速度;vD表示铰链点D 的速度矢量;vE表示铰链点E 的速度矢量;vG表示铰链点G 的速度矢量;vH表示铰链H 点的速度矢量。则

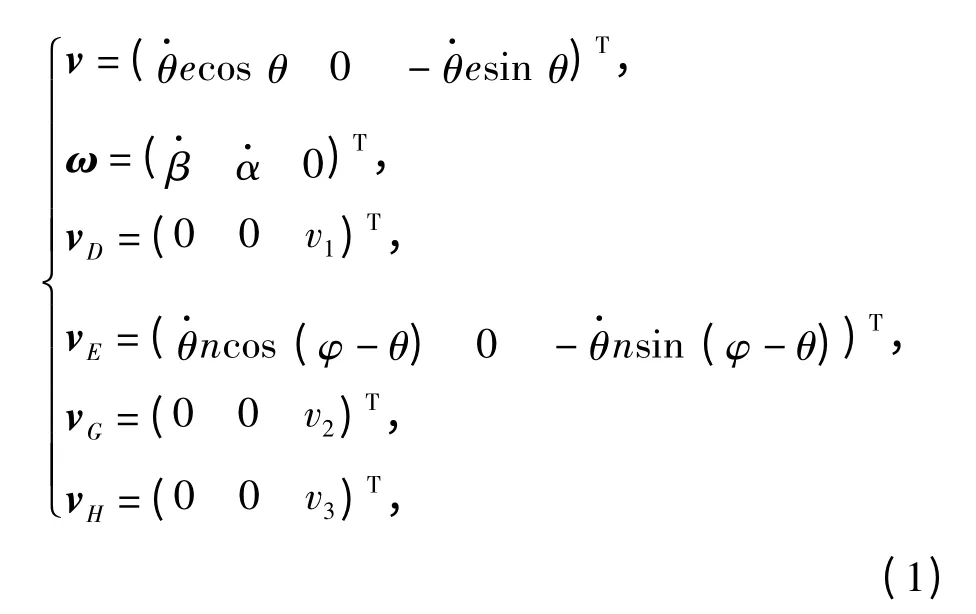
式中:α、β 分别为动坐标系统固定坐标系的Yb轴、Xb轴转过的角度。

设rDE为铰链点D 到铰链点E 的矢量，可得

已知

式中:Eb、Db分别为基坐标系下E 点、D 点的位置矢量。由(1)式、(2)式、(3)式可得

设:rJM、rGM、rJN、rHN分别为铰链点J 到铰链点M的矢量，铰链点G 到铰链点M 的矢量，铰链点J 到铰链点N 的矢量，铰链点H 到铰链点M 的矢量，vM表示铰链点M 的速度矢量，vN表示铰链点N 的速度矢量，可得

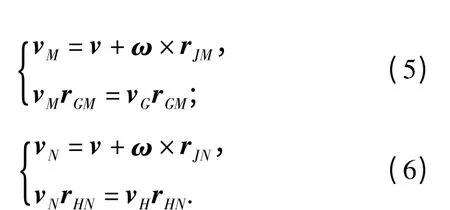
已知

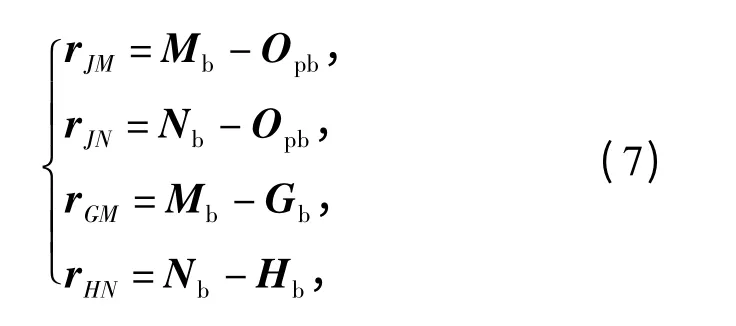
式中:Mb、Nb、Opb、Gb、Hb分别为基坐标系下各点的位置矢量。

由(1)式～(7)式可得

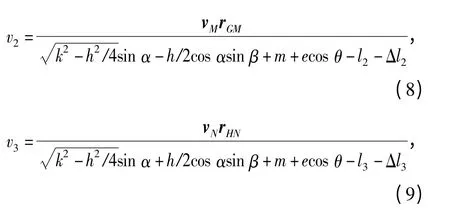
式中:

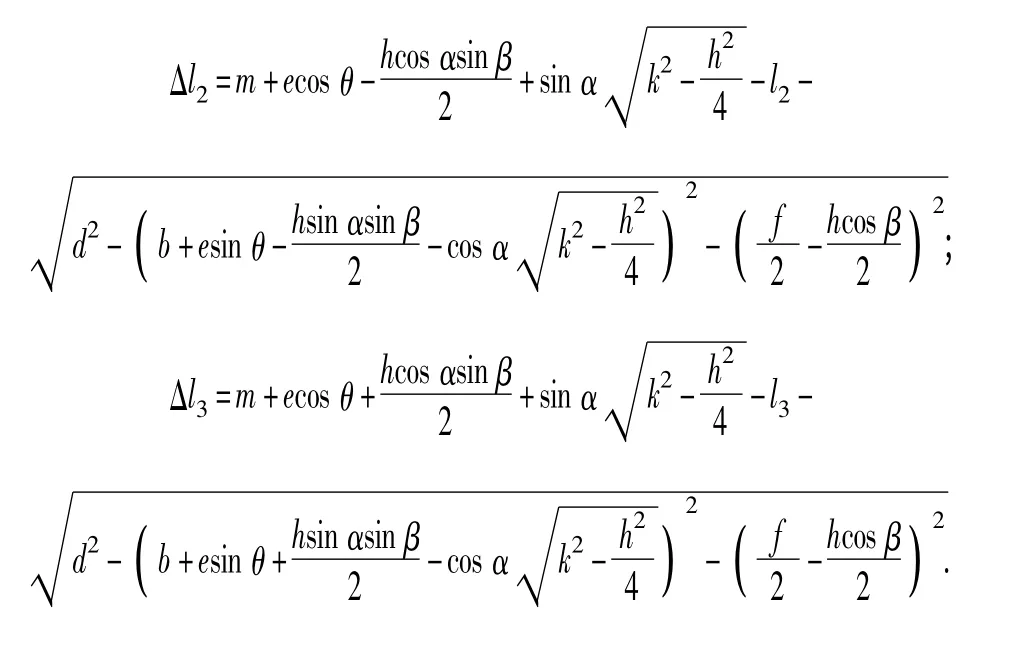
把(4)式、(8)式、(9)式写成统一的形式为

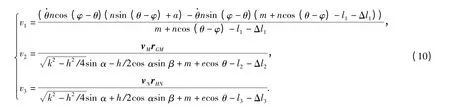
3 动力学建模

在运动学的基础上已求得各个点的位置矢量，动坐标系{P}在基坐标系{B}下的转换矩阵T 以及线速度雅可比矩阵Jv和角速度雅克比矩阵Jω. 根据拉格朗日方程，有

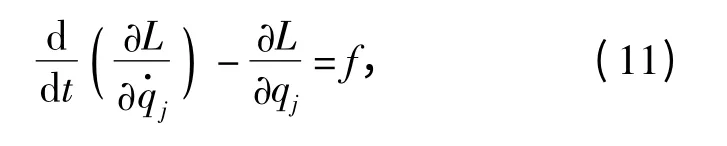
式中:L=P -U 表示拉格朗日函数，P 是系统的动能，U 是系统的势能;qj为广义坐标，qj=(z1z2z3)T，z1、z2、z3分别为移动副P1、P2、P3在Zb方向的位置矢量;为广义坐标的一阶导数，即为对应于广义坐标的广义力。

设3 个移动副Pi，i =1，2，3 的质量分别为m1、m2、m3，速度分别为v1、v2、v3，则3 个移动副的总动能为

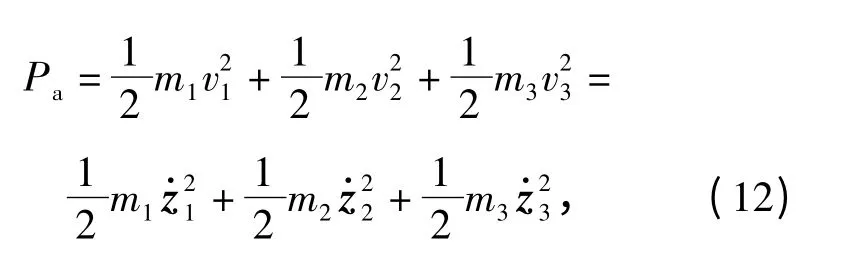
所以移动副总动能的广义坐标表达为

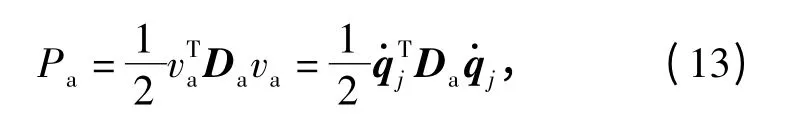
式中:Da=diag(［m1m2m3］);va=设从动杆DE、EF、FOp、GM、HN 的质量分别为mDE、mEF、mFOp、mGM、mHN，由机械腿结构布局特点可知

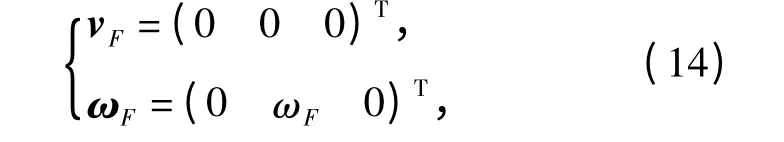
则铰链点Op的速度

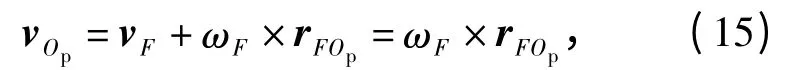
式中:rFOp为铰链点到铰链点Op的矢量;ωF为杆EFJ绕铰链F 点转动的角速度，并用vF表示铰链F 点的速度矢量。则

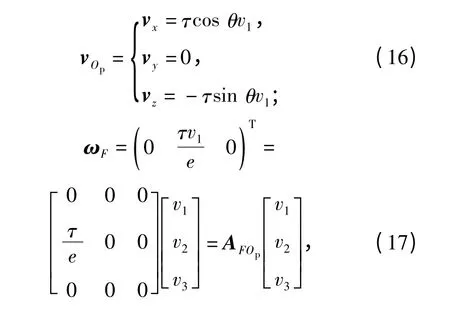
杆FOp的动能为

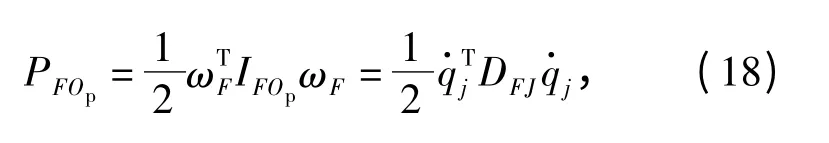
式中:IFOp为杆FOp的转动惯量;

杆EF 与杆FOp的转动速度相等，杆EF 的动能为

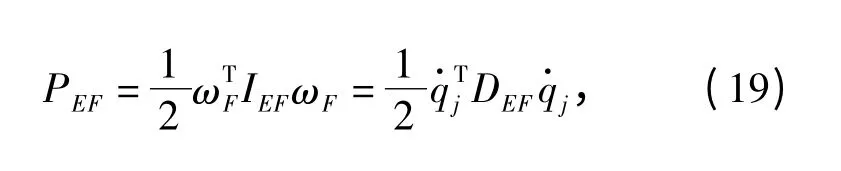
式中:IEF为杆EF 的转动惯量;

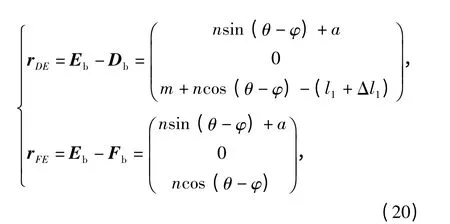
式中:rDE、rFE分别为铰链点D 到铰链点E 的矢量和铰链点F 到铰链点E 的矢量。

设铰链点E 的速度矢量为vE，杆DE 绕点D 的转动速度为ωD，则

把(17)式、(20)式代入(21)式整理得

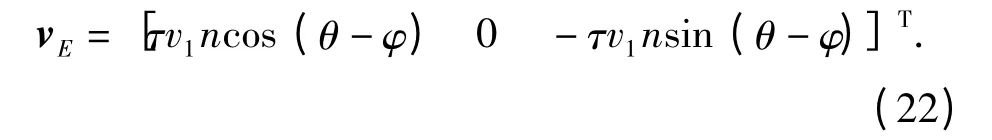
设DE 杆质心的速度矢量为vDE，则

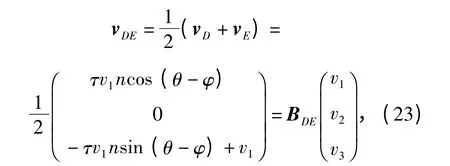
式中:BDE=杆DE 的动能为

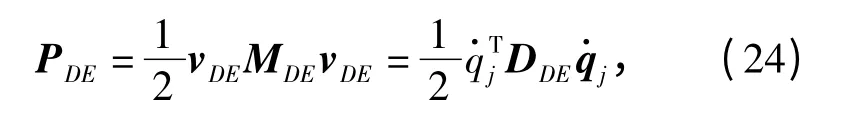
式中:DDE=BTDEMDEBDE，MDE为杆DE 的质量矩阵，MDE=diag(［mDEmDEmDE］).

vM和vN表示铰链M 和N 点的速度矢量，rJM和rJN分别为铰链点J 到铰链点M 和N 的矢量，以vG和vH表示铰链G 和H 点的速度矢量，rGM和rHN分别为铰链点G 到点M 和铰链点H 到点N 的矢量，ωG、ωH、ω 分别为杆GM、HN 和动平台的转动速度，有

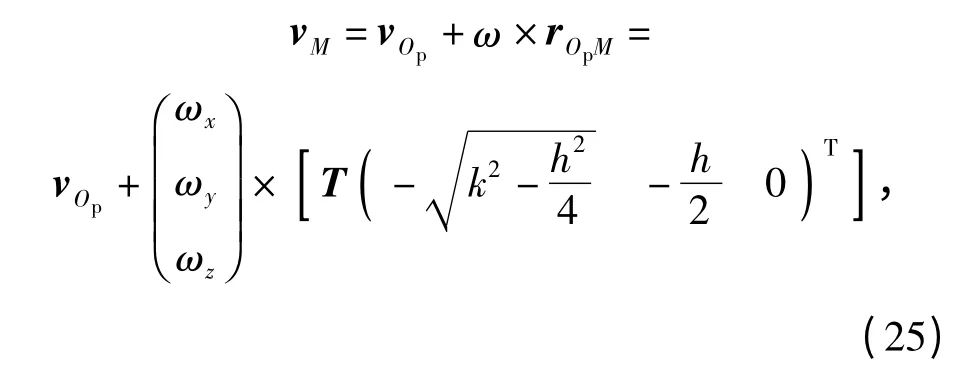
由(25)式得

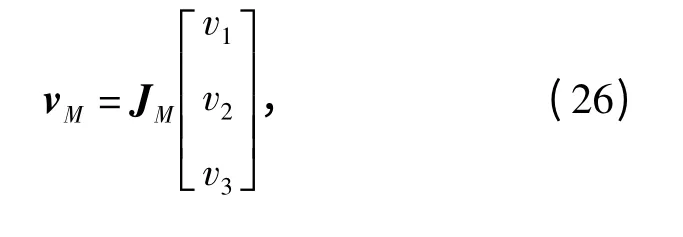
式中:JM=

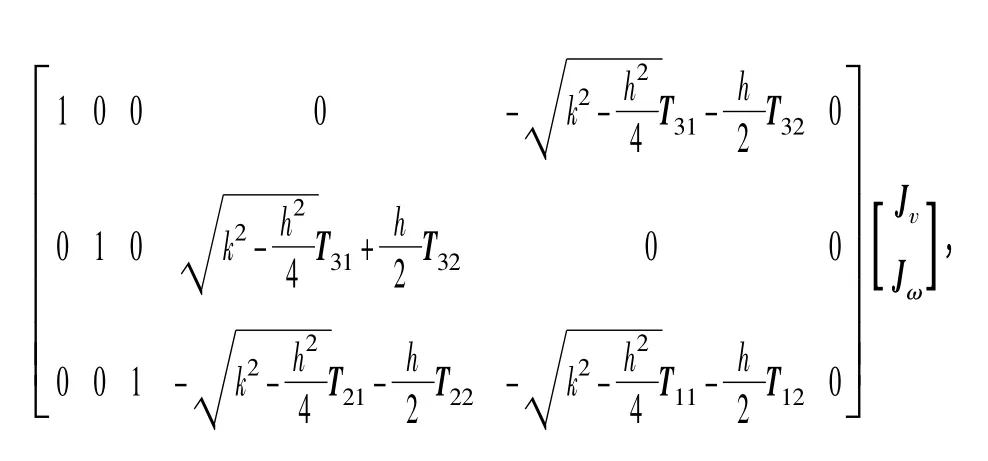
Ti，j为姿态转换矩阵T 的第i 行、第j 列，i、j=1，2，3.则GM 杆质心点的速度为

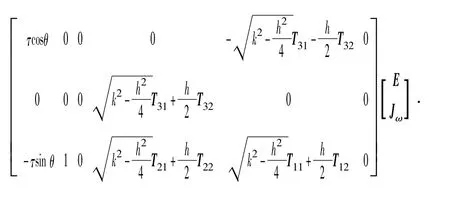
杆GM 的动能为

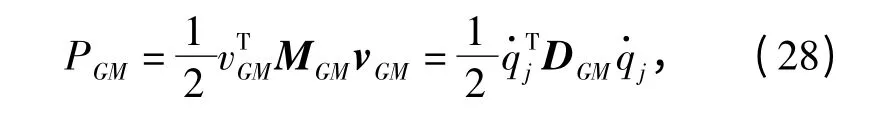
式中:DGM=JTGMMGMJGM，MGM为杆GM 的质量矩阵，MGM=diag(［mGMmGMmGM］).

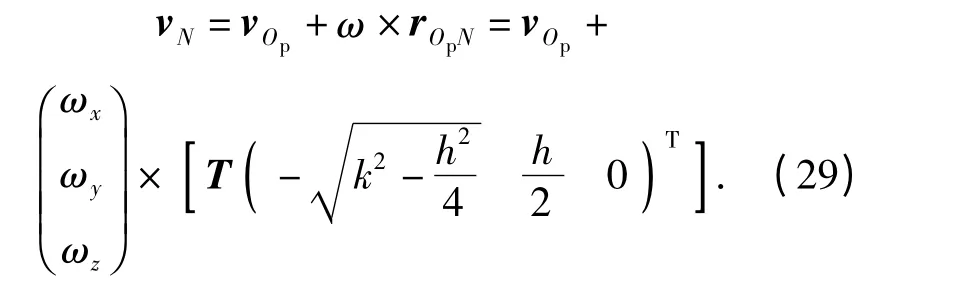
由(29)式得

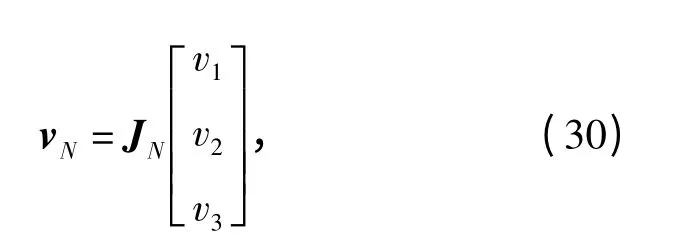
式中:JN=

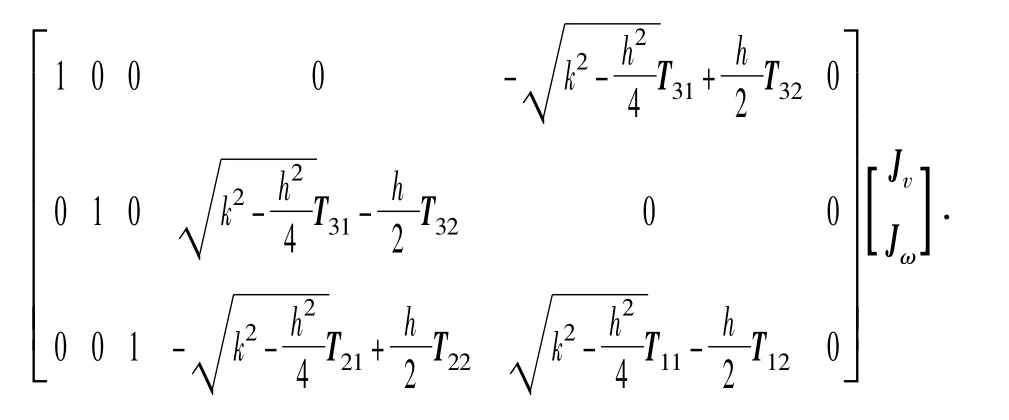
则HN 杆质心点的速度为

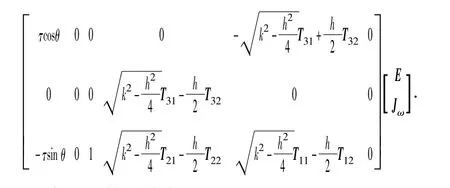
杆HN 的动能为

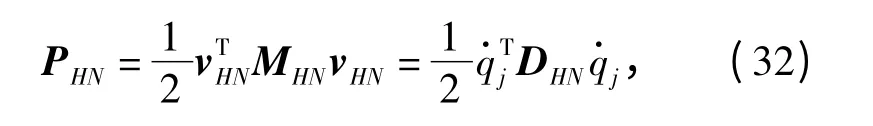
式中:DHN= JTHNMHNJHN，MHN为杆HN 的质量矩阵，MHN=diag(［mHNmHNmHN］).

设动平台的质量为md，Id为运动平台相对于固定坐标系{B}的惯量矩阵，质心的速度矢量为

已知速度雅克比矩阵为

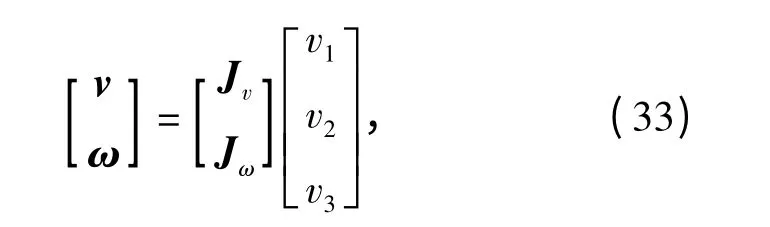
则动平台质心点的速度vd为

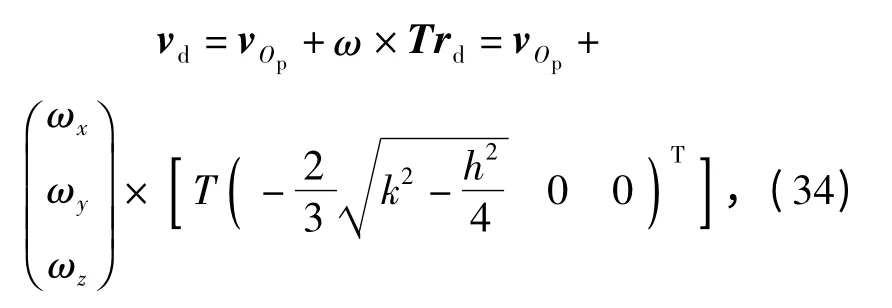
式中:rd为在动坐标系{P}下点Op到动平台质心点的矢量。

由(33)式、(34)式可得

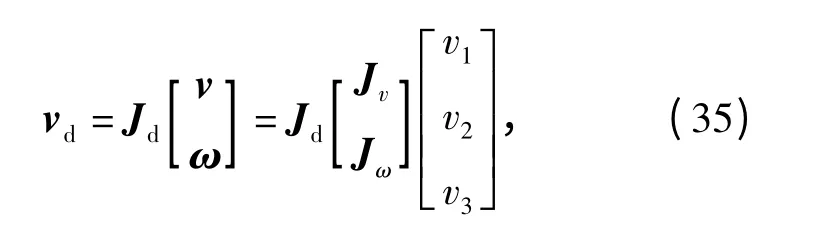
式中:Jd=

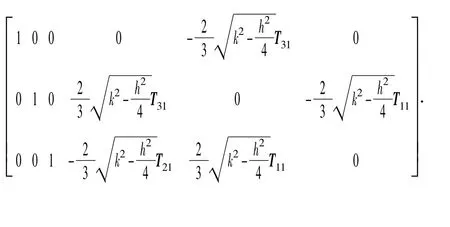
则动平台的动能为

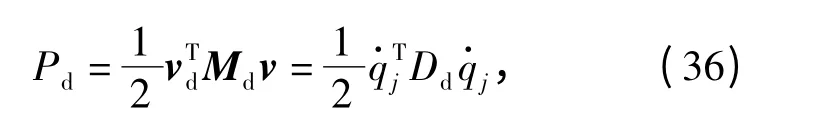
由(12)式、(18)式、(19)式、(24)式、(28)式、(32)式和(36)式可得系统总的动能为

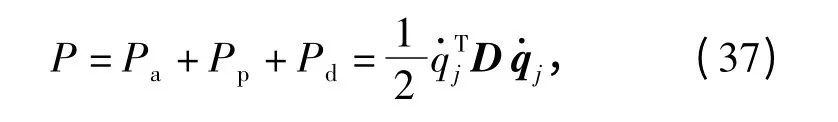
式中:D=Da+DFJ+DEF+DDE+DGM+DHN+Dd.

取ObXbYb面为零势能面，则系统的势能为0.

将系统总动能P 代入拉格朗日方程得

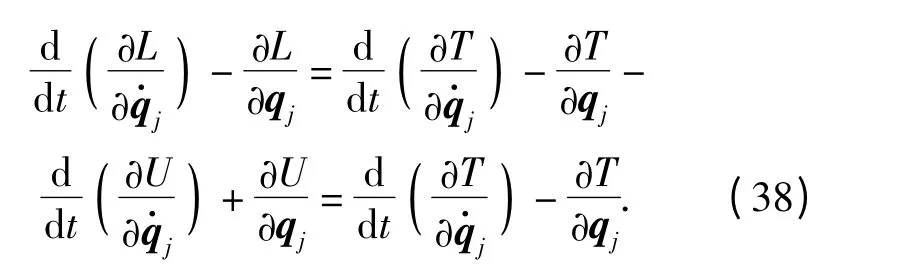
首先对广义坐标z1进行运算，则

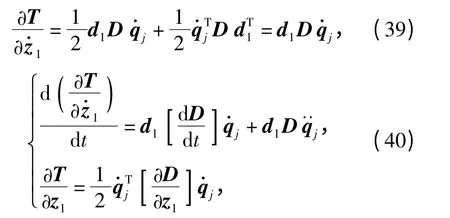
式中:d1=(1 0 0)，为对广义坐标的偏导［20-21］。

令M1=d1D，同理可求M2=d2D，M3=d3D，其中d2=(0 1 0)，d3= (0 0 1)，分别为=对和的偏导数。则机械腿惯性矩阵为

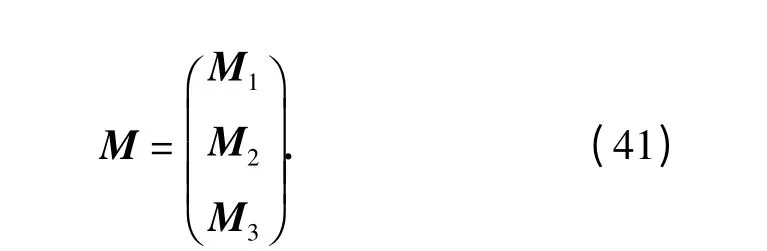
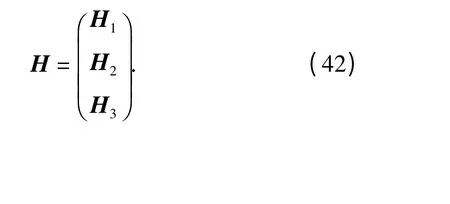
将该机构的动力学方程写成如下一般形式:

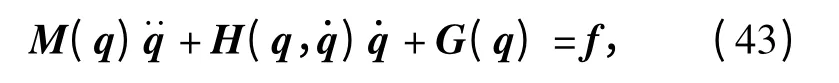
4 伺服电机峰值预估模型

4.1 伺服电机转速预估

驱动3 个移动副的3 个伺服电机分别通过联轴器与丝杠连接，移动副与丝杠螺母固定联接，如图2所示。电机的转动带动丝杠的转动，丝杠只转动不移动，与丝杠配合的丝杠螺母产生直线位移，从而带动移动副移动，最终实现膝关节和踝关节的运动形式。

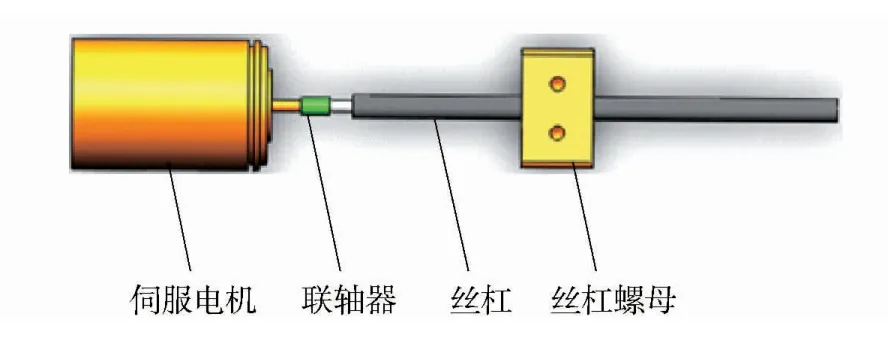
图2 伺服电机驱动结构图Fig.2 Driving structure of servo motor

选用单线螺纹丝杠，材料为45 号钢，螺距p =1.25 mm，公称直径d =8 mm，螺纹为梯形粗牙普通螺纹，牙形角λ=30°.

前面已求出3 个直线移动副的移动速度与膝关节和踝关节转动角度的关系，移动副的运动是由电机转动通过丝杠传动传递过来的，因为移动副的运动方式是直线运动，所以要求电机的转动速度需要根据丝杠传递运动的特点把线速度转换成角速度。

设3 个电机的转动角速度分别为ω1、ω2和ω3，分别对应于移动副P1、P2、P3. 易得电机的转动速度等于丝杠的转动速度，由丝杠传递运动的特点可得

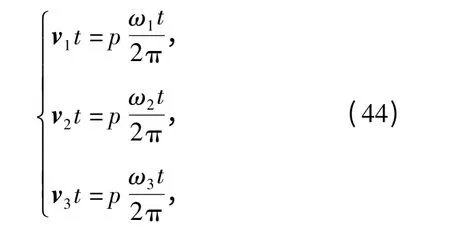
所以

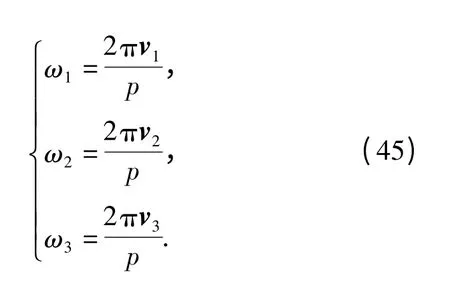
(45)式即为电机转动速度与膝关节和踝关节转动角度之间的关系式。

4.2 伺服电机转矩预估

由(43)式，伺服电机驱动力的表达式为

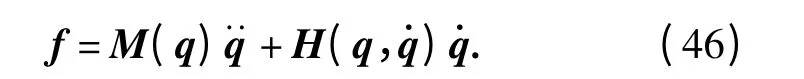
由运动反解可得

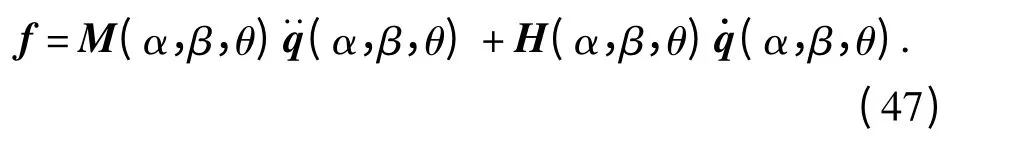
考虑到伺服电机快速启动的情况，可以忽略(43)式中的哥氏力和离心力项，伺服电机的峰值力为

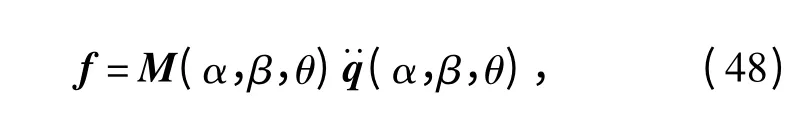
则

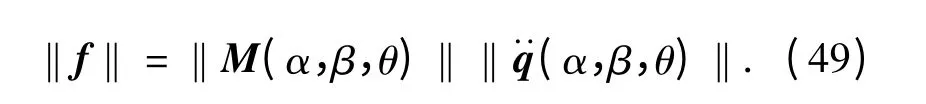
由于M(q)都随姿态变化，因此取它们的全域最大值来抵抗哥氏力和离心力项引起的负载力矩。因此，伺服电机峰值力预估模型为

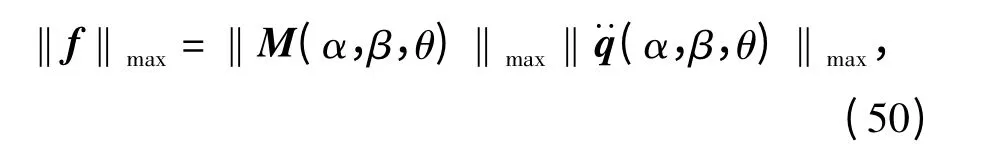
计算可得3 个电机的最大驱动力

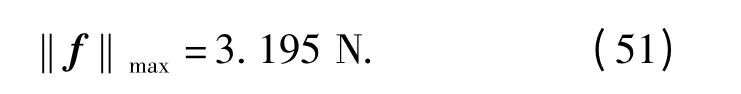
在(48)式中，左边的f 为广义力，广义坐标选取不同，则广义力所代表的含义不同。如果选取动平台的转动角度作为广义坐标，那么根据动力学模型所求得的广义力不是驱动力，还要乘以一个关节空间与操作空间的力雅克比矩阵。对于该机械腿机构，选取3 个移动副的输入位移作为广义坐标，那么广义力f 的大小就是电机驱动力的大小，不用再求解力雅克比矩阵。在(48)式中，已知的是α、β、θ 的运动规律，在运动反解中已求得α、β、θ 与广义坐标的关系，所以可很容易地求出广义力f 的大小。

因为电机是通过丝杠把电机的转矩转换成移动副的驱动力，所以要把移动副所受的驱动力f 转换成转矩，力与力矩之间的转换关系式为

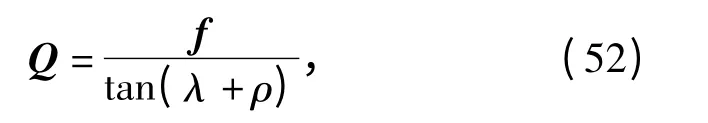
式中:Q 表示转矩;ρ 为丝杠螺纹表面的摩擦角。

本文选取的丝杠螺纹为梯形螺纹，所以牙形角λ=30°，与螺纹的升角相等。丝杠的材质选择45 号钢调质处理，丝杠传动选择动摩擦，有润滑剂，摩擦系数取值范围为0.05 ～0.10，这里取0.08，所以摩擦角为

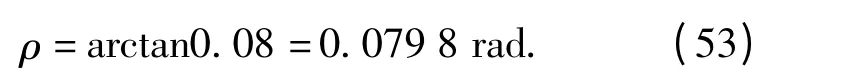
由(52)式、(53)式得

由(51)式、(54)式可得电机峰值预估最大驱动力矩

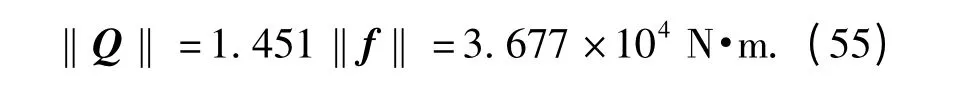
5 实例分析与仿真

机械腿所采用参数如下:a =150 mm，b =300 mm，c=150 mm，d=440 mm，e =440 mm，f =300 mm，h =300 mm，k = 320 mm，m = 440 mm，n = 180 mm，l1=200 mm，l2=440 mm，l3=440 mm，φ=120°.

机械腿的3 个转动角θ、α 和β 的运动规律为

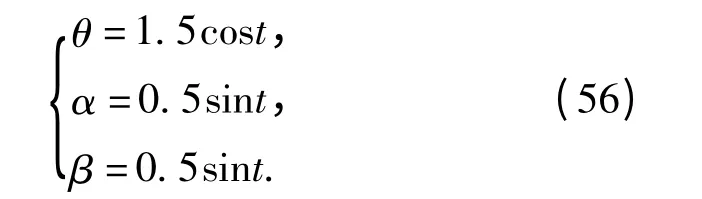
这里取丝杠螺纹为单线，借助于MATLAB 进行仿真，伺服电机的转速变化规律和转矩变化规律分别如图3和图4所示。

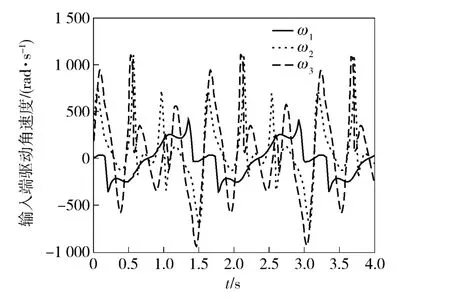
图3 3 个伺服电机转速变化曲线Fig.3 Speed change curves of 3 servo motors

从仿真结果可看出，3 个伺服电机的转速和转矩均为周期性变化，并且电机最大力矩小于电机峰值预估最大力矩。伺服电机转速的变化与膝关节和踝关节转动角度有关，也与丝杠的线数有关;驱动力矩的大小与丝杠的选取有关，比如丝杠螺纹的线数，丝杠的材质，有无润滑等等，它还与给定的膝关节和踝关节的转动角度有关。

6 结论

1)对一种并联拟人机械腿机构进行运动反解分析，给出了输入速度与输出速度之间的映射关系。

2)利用拉格朗日方法建立了该机构的动力学模型，并基于该模型建立伺服电机的预估模型。

3)对伺服电机预估模型进行仿真分析，仿真结果表明电机速度和转矩均为周期性变化，为电机选型奠定理论基础。

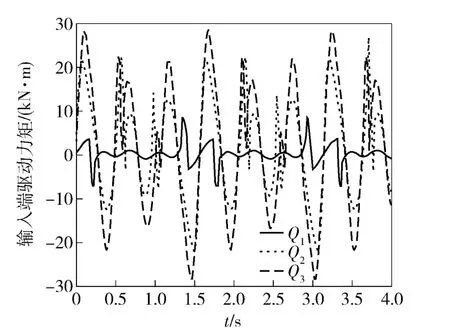
图4 3 个伺服电机转矩变化曲线Fig.4 Torque change curves of 3 servo motors

References)

［1］ 李研彪，刘毅，计时鸣，等. 新型拟人机械腿的参数优化［J］.中国机械工程，2013，24(9):1239 -1245.LI Yan-biao，LIU Yi，JI Shi-ming，et al. Parameter optimization for a novel mechanical leg［J］. China Mechanical Engineering，2013，24(9):1239 -1245.(in Chinese)

［2］ 李晓冬. 并联机器人的特点及应用分析［J］. 黑龙江科技信息，2008，1(5):36 -37.LI Xiao-dong. The characteristics and application analysis of parallel robot［J］. Heilongjiang Science and Technology Information，2008，1(5):36 -37.(in Chinese)

［3］ 李研彪，刘毅，赵章风，等. 基于空间模型技术的拟人机械腿的运动学传递性能分析［J］. 农业工程学报，2013，29(2):17 -23.LI Yan-biao，LIU Yi，ZHAO Zhang-feng，et al. Kinematics transmission analysis on anthropopathic mechanical leg based on spatial model technique［J］. Transactions of the Chinese Society of Agricultural Engineering，2013，29(2):17 -23.(in Chinese)

［4］ 黄真，赵永生，赵铁石. 高等空间机构学［M］. 北京:高等教育出版社，2006.HUANG Zhen，ZHAO Yong-sheng，ZHAO Tie-shi.Advanced spatial mechanism. ［M］. Beijing:Higher Education Press，2006.(in Chinese)

［5］ Gao F，Wang G F，Cui Y，et al. Dynamic modeling and analysis of 9-DOF omnidirectional legged vehicle［J］. Chinese Journal of Mechanical Engineering，2011，24(4):515 -521.

［6］ 张典范. 新型6-(P-2P-S)并联机器人动力学建模及其运动控制研究［D］. 秦皇岛:燕山大学，2009:39 -46.ZHANG Dian-fan. Dynamics modeling and motion control analysis of noval 6-(P-2P-S)parallel robot［D］. Qinhuangdao:Yanshan University，2009:39 -46.(in Chinese)

［7］ Rim B，Habib N，Hala B，et al. Dynamic modeling and control of a multi-fingered robot hand for grasping task［J］. Procedia Engineering，2012，41:923 -931.

［8］ Amira A，Olfa B. A relevant reduction method for dynamic modeling of a seven-linked humanoid robot in the three-dimensional space［J］. Procedia Engineering，2012，41:1277 -1284.

［9］ Arsenault M，Gosselin C M，Saravanan S. Kinematic，static and dynamic analysis of a planar 2-DOF tensegrity mechanism［J］.Mechanism and Machine Theory，2006，41(9):1072 -1089.

［10］ Bai Z F，Han X G，Chen W Y. Study of a 3-DOF parallel manipulator dynamics based on Lagrange equation［J］. Journal of Beijing University of Aeronautics and Astronautics，2004，30(1):51 -54.

［11］ Rong F F，Ying S K，Guo C W. Dynamic analysis and system identification of an LCD glass-handling robot driven by a PMSM［J］.Applied Mathematical Medelling，2009，34(5):1360 -1381.

［12］ 王红旗，王泰华. 基于旋量理论的移动机械手动力学建模［J］.兵工学报，2010，31(6):849 -854.WANG Hong-qi，WANG Tai-hua. Dynamic modeling of mobile manipulator based on scerw theory［J］. Acta Armamentarii，2010，31(6):849 -854.(in Chinese)

［13］ Lee J D，Geng Z. A dynamic model of a flexible Stewart platform［J］.Computers and Structures，1993，48(3):367 -374.

［14］ Cheroutre-Vialette M，Lebert A. Growth of Listeria monocytogenes as a function of dynamic environment at 10 ℃and accuracy of growth predictions with available models［J］. Food Microbiology，2000，17(1):83 -92.

［15］ Miller K. Experimental verification of modeling of DELTA robot dynamics by direct application of Hamilton's principle［C］∥Proceedings of 1995 IEEE International Conference on Robotics and Automation. Nagoya-shi，Japan:IEEE，1995:532 -537.

［16］ 谢庆华，张琦，杨小川. 液压排雷机械手作业系统的运动学分析［J］. 兵工学报，2004，25(5):572 -575.XIE Qing-hua，ZHANG Qi，YANG Xiao-chuan. Kinematic analysis of mine clearing manipulator operation of the hydraulic system［J］. Acta Armamentarii，2004，25(5):572 - 575. (in Chinese)

［17］ 金振林，崔冰艳. 机器人肩关节的动力学建模及伺服电机峰值预估［J］. 农业工程学报，2011，27(8):145 -149.JIN Zhen-lin，CUI Bing-yan. Dynamic modeling and peak prediction of servo motor for shoulder joint of robot［J］. Transactions of the Chinese Society of Agricultural Engineering，2011，27(8):145 -149. (in Chinese)

［18］ 荣誉，金振林. 3-DOF 并联机械腿动力学建模与伺服电机峰值预估［J］. 光学精密工程，2012，20(9):1974 -1983.RONG Yu，JIN Zhen-lin. Dynamic modeling of 3-DOF parallel mechanical leg and peak prediction of servo motor［J］. Optics and Precision Engineering，2012，20(9):1974-1983.(in Chinese)

［19］ 李金泉，杨向东，付铁. 码垛机器人机械结构与控制系统设计［M］. 北京:北京理工大学出版社，2011.LI Jin-quan，YANG Xiang-dong，FU Tie. Mechanical structure and control design of palletizing robot［M］.Beijing:Beijing Institute of Technology Press，2011.(in Chinese)

［20］ 王跃灵. 拟人机械臂动力学建模与智能控制研究［D］. 秦皇岛:燕山大学，2010.WANG Yue-ling. Dynamics modeling and intelligent control for humanoid mechanical arm［D］. Qinhuangdao:Yanshan University，2010.(in Chinese)

［21］ 施毅. 新型五自由度并联机床的若干基础问题及动力学分析［D］. 秦皇岛:燕山大学，2005.SHI Yi. Some foundation issues and dynamics analysis of a novel 5-DOF parallel machine tool［D］. Qinhuangdao:Yanshan University，2005.(in Chinese)