使用香农熵的心外膜电信号相关性分析
2014-02-28杨翠微
张 璘,杨翠微
1 复旦大学专用集成电路与系统国家重点实验室,上海市,200433
2 复旦大学电子工程系,上海市,200433
使用香农熵的心外膜电信号相关性分析
【作 者】张 璘1,2,杨翠微2
1 复旦大学专用集成电路与系统国家重点实验室,上海市,200433
2 复旦大学电子工程系,上海市,200433
该文利用了互相关系数香农熵值对实验犬的左右心房前壁心外膜电信号进行了分析。结果显示在窦性心律下,左房前壁的心外膜电信号的相关性稳定程度比右房前壁的心外膜电信号高;在房颤心律下,虽然左右房前壁心电信号相关性稳定程度都有所下降,但是仍然有部分区域保持较稳定的相关性。这有助于进一步了解房颤心律下心电信号的相关性。
心外膜电信号;相关性;香农熵
0 引言
心房颤动(房颤),作为最常见的室上性心律失常疾病,很大程度地增加了病人发生心源性栓塞和中风的危险[1]。在过去,人们认为,房颤心律下的心脏电活动是随机而杂乱无章的。但是,随着近年来研究的不断深入,人们发现房颤心律下的心房电活动仍然具有一定的组织性和同步性[2]。相邻通道间信号的互相关系数常被用作评判信号相关性的指标,在窦性心律下,心房电信号之间的相关性较好,通道间信号的互相关系数较高且稳定。在房颤信号心律下,心房的电活动较为杂乱,信号的相关性降低且变化频繁,从而相邻信号间的互相关系数不稳定。本文利用香农熵作为评判心电信号相关稳定性的指标,研究在不同心律下,左右心房所产生电信号的相关性的情况,寻找在房颤心律下具有较稳定相关性的心房组织区域,帮助我们进一步了解房颤心律下心脏电活动的相关性特性。
1 数据采集
1.1 信号采集
本文分析的数据来源于4只动物犬的心外膜电信号,采集系统是采用复旦大学电子工程系心脏电生理与起搏实验室所设计的128道心外膜电位标测系统[3],所有电极采集的心外膜电信号都经过增益为25~2 000的独立放大器和(3.5~600)Hz的带通滤波的处理,以2 kHz的采样率进行数据采样,以16 bit分辨率进行存储。本次研究主要分析从左房前壁和右房前壁所采集到的心外膜电信号,电极片在心脏上的位置如图1所示。

图1 心外膜采集系统电极位置示意图Fig.1 The electrode position of Epicardial Mapping System
整个实验是基于类胆碱能的房颤模型进行的。房颤是由刺激频率为20 Hz,脉冲宽度为2 ms的脉冲信号对心房组织进行连续5 s的持续刺激所诱发的。刺激信号通过一对安放在右心房以及右心房与上腔静脉交接处的刺激电极进行传输。我们记录了刺激前窦性心律下的心外膜电信号以及房颤过程超过3 min的房颤心外膜电信号。对于窦性心律和房颤心律,每只狗平均各选用100段心外膜电信号数据,每段数据的长度为20 s。
1.2 信号预处理
无论在窦性心律还是房颤心律下,心外膜标测系统采集到的心外膜电信号都包含心房电信号和心室电信号,为了消除心室电信号对数据分析产生的影响,我们采用了一种基于最小均方误差(LMS)准则的自适应滤波算法[4],将心室信号(噪声)从采集到的心外膜电信号中去除(实验中采集了1路左室心尖的心外膜信号作为噪声信号)。
2 基于互相关的香农熵算法设计
2.1 不同心律下的心外膜电信号的相关性
心房电信号间的相关性大小能够反映出不同心肌组织参与除极波传导的相关程度。在本文中,心房电信号间的相关性通过计算相邻通道间(按照电极片上电极具体的位置)信号的互相关系数进行评价。在窦性心律下,自发的心电信号由窦房结产生,然后按照特殊的传导路径有秩序地传播到所有的心肌组织,各部分的心房组织有秩序地参与到除极波传导过程中,信号间的相关性较强,则相邻通道间的心电信号的互相关系数较高且稳定;在房颤心律下,由于异位兴奋灶或是折返回路的存在,心房电活动较为杂乱,同一个心房组织可能受到一个或多个除极波传导的影响,所以信号间的相关性较弱,从而相邻通道间的心电信号互相关系数较低,而且不稳定。本文采用了香农熵[5]对信号的互相关值的稳定程度(或相反的离散程度)进行评判。方法如下:
(1) 将每两个相邻电极点所采集到的20 s心外膜电信号数据记为Data_i,Data_j;
(2) 对两段数据进行互相关系数计算,得到互相关系数中模最大的值记为CrossCorr(i, j);
(3) 对于两个固定的相邻通道i和j而言,统计其100段数据的互相关系数在分组中出现的概率p(i),以每组的统计概率计算其相关性的香农熵值SE =-p(i)×ln p(i)。
在窦性心律下,心房信号之间的相关性较高,相邻通道信号间的互相关系数高且稳定,所以在进行互相关系数香农熵的计算时,由于互相关系数比较稳定,导致互相关系数较高值出现的概率大,而互相关系数较低值出现的概率较小,互相关系数的分布较为集中,从而计算出的互相关系数香农熵比较低。然而,在房颤心律下,心房信号之间的相关性较低,反应在相邻两通道间的互相关系数也较低,同时互相关系数不稳定、随着时间变化的范围较大、分布较分散,所以在进行互相关系数的香农熵计算时,出现在各个分组的互相关系数概率较为随机,所以在房颤心律下的心房电信号互相关系数的香农熵值比较高。
3 基于香农熵的心房电信号的相关性研究结果
3.1 基于香农熵的窦性心律下心房电信号相关性分析
所有100段数据的互相关系数的香农熵值都针对本次实验犬数据所对应的最大香农熵值进行了归一化处理,由归一化后的香农熵值分布图(图2)展示了在窦性心律下左房前壁与右房前壁的心外膜电信号的互相关系数相对香农熵值,从图2可以看出,相对于右房前壁的心房电信号而言,左房前壁的心房电信号的香农熵较低(深色),则右房前壁的心外膜电信号具有高香农熵的区域较多(浅色)。说明在窦性心律下,左房前壁的心房电信号的相关性比右房前壁的心房电信号相关性好。但是根据在右房前壁上仍然有一些区域的香农熵值较低,由于实验犬存在个体差异性,所以同样在窦性的心律下,动物的左右房前壁的相关性程度也存在一定的差异。

图2 窦性心律下左右房前壁心外膜电信号互相关系数的香农熵分布Fig.2 The distribution ofShannon Entropy of the cross correlation of epicardial signals from anteriorwall of atria during atrial fi brillation
3.2 基于香农熵的房颤心律下心房电信号相关性分析
图3展示了在房颤心律下,左右房前壁的心电信号的互相关系数香农熵值的分析结果。可以从图3看出,当心律从窦性心律转变为房颤心律时,心电信号的香农熵值很大程度地变高了,即左右房前壁的心电信号在房颤心律下的相关性都随之而降低。特别对于左房前壁而言,在窦性心律时,心电信号保持较为稳定的相关性,从而香农熵值较低(深色);然而,在房颤心律下,心电信号的相关性降低且不稳定,从而导致互相关系数值的分布就比较混乱,评判相关性离散程度的香农熵值就随之增大。

图3 房颤心律下左右房前壁心外膜电信号互相关系数的香农熵分布Fig.3 The distribution of Shannon Entropy of the cross correlation of epicardial signals from anteriorwall of atria during sinus rhythm
3.3 房颤心律下心房电信号相关性
在房颤心律下,左右房前壁的心外膜电信号的互相关系数降低,对于大部分的左右房前壁组织而言,互相关系数的香农熵值较高,心电信号的互相关系数较为离散。但是,对于4只实验犬而言,总会有某些区域的心肌组织具有较低的互相关系数香农熵。这些互相关系数香农熵值较低的区域具有稳定的心电信号相关性,对于在房颤心律下心电活动的研究具有重要的作用。所以我们以犬1为例在图4和表1中展示了在房颤心律下具有较低互相关系数香农熵区域所对应的的具体互相关系数。同时,在表1中,我们可以看到同样是香农熵值较低信号的互相关系数,其互相关系数值也可能出现高低差异的不一样,对于互相关系数较高且稳定(香农熵值较低)的通道,例如CrossCorr(43-44)和 CrossCorr(34-40)等,说明相应的心肌组织在房颤时参与除极波电活动的相关性程度较强。在手术过程中,这些心肌区域都应该引起我们的注意。
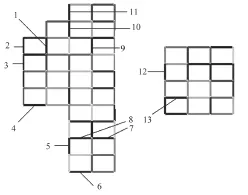
图4 房颤心律下左右房前壁互相关系数Fig.4 The Cross Correlation of theanterior wall of atria during atrial fi brillation

表1 部分对应通道的互相关系数值Tab.1 The corresponding cross correlation value of partial channel
4 总结
利用互相关系数香农熵的方法,我们能够评价在窦性心律和房颤心律下的心房电信号相关性的稳定程度,对于标测系统而言,能够快速地找出信号相关性较为稳定的区域,进而再结合相应心房部位具体的相关性参数(如:互相关系数),增强我们对于在房颤心律下心房电活动相关性的了解,进而在未来为房颤手术的消融治疗提供指导。
[1] Abbott WM, Maloney RD, McCabe CC, et al. Arterial embolism: a 44 year perspective[J]. AmJSurg, 1982, 143(4): 460-464.
[2] Sih HJ, Zipes DP, Berbari EJ, et al. A high-temporal resolutionalgorithm for quantifying organization during atrial fi brillation[J]. IEEE Trans Biomed Eng, 1999, 46(4): 440-50.
[3] Yang CW, Lu WJ, Zhou T, et al. Development of epicardial mapping systemfor studying atrial fi brillation[C]. Int Conf Biomed Eng Inform, 2008: 606-609.
[4] 孙莉倩, 刘梁, 王彦磊, 等. 一种适用于全心房心外膜标测中抑制心室干扰的自适应滤波算法[J]. 中国医疗器械杂志, 2011, 35(4): 243-245.
[5] Shannon CE. A mathematical theory of communication[J]. ACM Sigmob Mobil Comput Communicat Review, 2001, 5(1): 3-55.
The Correlation Analysis of the Epicardial Signals by Shannon Entropy
【 Writers 】Zhang Lin1,2, Yang Cuiwei2
1 National Key Laboratory of ASIC and System, Fudan University, Shanghai, 200433
2 Department of Electronic Engineering, Fudan University, Shanghai, 200433
【 Abstract 】This paper applied the Shannon Entropy based on the cross correlation to analyze the epicardial signals from anterior wall of the canine atria. The result demonstrated that during sinus rhythm, the stability level of the correlation among signals from anterior right atria is much higher than the signals from anterior left atria. All the signals from the anterior wall descended when the rhythm changed from sinus rhythm to atrial fi brillation(AF). However, there were some regions still having a stable correlation during AF. The results will be helpful to enhance understanding of the correlation characteristic of AF.
epicardialsignal, correlation, Shannon Entropy
R541.75
A
10.3969/j.issn.1671-7104.2014.03.002
2013-12-26
国家自然科学基金(61071004)
杨翠微,E-mail: yangcw@fudan.edu.cn
1671-7104(2014)03-0165-03
