一种新型水下爆炸冲击等效加载实验方法

杨一方, 郭 锐, 刘萌萌, 刘荣忠



一种新型水下爆炸冲击等效加载实验方法

杨一方1, 郭 锐1, 刘萌萌2, 刘荣忠1

(1. 南京理工大学 智能弹药技术国防重点学科实验室, 江苏 南京, 210094; 2. 豫西工业集团, 河南 南阳, 473000)

针对传统水下爆炸冲击响应实验研究中存在的问题, 提出了一种实验室仿真水下爆炸冲击的等效加载方法, 通过飞片撞击的方式来获得水下爆炸冲击等效载荷。同时建立了等效理论模型与流固耦合数值仿真来进行对比分析。结果表明, 数值仿真结果与理论分析结果吻合较好, 通过调节飞片的撞击速度与撞击比质量可以获得不同水下爆炸冲击所需要的等效载荷, 进而为鱼雷爆炸对典型舰船结构的冲击响应研究提供一种新的思路。

水下爆炸; 等效加载; 冲击响应; 流固耦合

0 引言

随着海洋事业的发展, 水下装备的抗冲击性能作为其生存能力的保障, 显得尤为重要。使用传统的防护方法来提高装备的生存能力会大大增加装备质量, 影响装备性能。近年来, 国内外学者提出了大量的新型夹层板结构以及新的复合材料作为其防护结构, 以提高装备的生存能力。由于复合材料冲击响应以及夹层板结构本身的复杂性, 难以对其进行理论研究, 对于夹层板来说, 只能对其中简单的结构进行理论建模分析, 对复杂结构主要通过实验以及数值仿真的方法进行研究。

目前, 国内外学者对该领域已有一些研究，Xue等采用简化理论对一些典型夹层板结构的动态压溃响应进行了分析[1-2]。Tilbrook采用实验与数值仿真相结合的方法对典型夹层板结构的动态压溃效应进行了分析[3]。Radford等采用泡沫铝撞击的方法模拟脉冲载荷[4], 该方法虽然能够产生类似冲击波的脉冲效果, 但不能模拟水下冲击的流固耦合效应。在水中使用炸药爆轰的方式来进行水下爆炸冲击响应实验的研究是目前运用最广泛的研究方式, 但该方法成本较高且实验可控性较差, 故实用性较差。针对传统研究方法中所存在的问题, Espinosa和项大林等人提出了一种等效水下爆炸冲击加载实验装置[5-6], 该装置主体为圆锥形水仓, 通过轻气炮系统发射飞片撞击圆锥形水仓获得冲击载荷, 装置复杂且成本较高, 单次实验需要较为复杂的操作流程, 且对被测试件有着较高的加工要求。本文提出了一种新型的等效水下爆炸冲击加载装置, 改变原来的水仓结构, 采用圆柱形水仓, 将活塞以及被测试件内置于水仓内, 简化水仓结构, 降低设备成本。当撞击所产生冲击波在圆锥形水仓内传播时, 由于传播路径为变截面路径, 冲击波在传播时会发生反射与透射, 对冲击波形成干扰, 极大地降低了等效水下爆炸冲击加载的效果, 因此, 采用圆柱形水仓可以避免冲击波在传播路径中的变截面问题, 避免此因素对冲击波的干扰。

1 建模与仿真

1.1 实验平台

所搭建的实验平台主要包括飞片发射系统、飞片测速系统、水仓和压力测量系统。其中飞片发射系统采用轻气炮系统为飞片提供初始动能, 将其加速至一定速度射出; 飞片飞行速度由测速系统测得; 飞片撞击在用于密封水仓的活塞上, 在水仓内形成初始冲击波, 该冲击波经水介质传递至后部试件上, 通过固定在水仓壁上的压力传感器测量并记录水仓内压力变化。

1.2 建立模型

首先建立实验平台的主体模型,由飞片、活塞、水仓、试件水及空气场等主要部分组成。利用专业网格划分软件Hypermesh建立模型, 并进行有限元网格划分, 模型结构示意图见图1。图中,飞片、活塞、试件及水仓内径均为直径40 mm的圆柱形, 活塞厚度为30 mm, 水仓内水柱长度为94 mm, 空气场包围水域。在计算时, 通过飞片撞击活塞的方式, 在水仓内产生冲击波, 通过使用不同长度的飞片以获得不同质量飞片撞击的结果。

图1 等效冲击加载数值仿真模型示意图

由于活塞、试件与水之间涉及流固耦合作用, 因此文中选用单点ALE积分算法来模拟活塞与水的相互作用, 以及水仓内波的传播情况, 对结构件采用Lagrange算法进行计算, 结构与水之间通过*CONSTRAINED_LAGRANGE_IN_SOLID关键字进行耦合。

1.3 材料模型和状态方程

由于飞片在撞击活塞时会发生形变, 且两者形变对真实结果影响较大, 为使计算结果最大限度地接近真实情况, 需选用合适的材料模型对材料进行描述。因此, 本文选用*MAT_PLASTIC_ KINEMATIC随动塑性材料模型描述飞片、活塞以及试件, 飞片、活塞及试件均选用铝制材料。水及空气场均采用* MAT_ NULL材料模型, 使用*EOS_LINEAR­_POLY_NOMIAL方程加以描述。由于在实际中水仓只起到约束作用, 故为节约计算资源, 节省计算时间将水仓壁设置为刚体。

2 理论分析

经过多年实验及理论研究, Zamyshlyaye和Cole得出水下爆炸冲击波压力衰减规律, 且经过大量工程实践证明了其准确性[7-8]。衰减规律为

在实验系统中, 由撞击产生平面波在水介质中传递。对于平面波, 各向同性均匀流体介质中压力与质点振动速度存在简单的线性关系

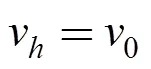
依据Deshpande研究成果[9], 时间衰减系数

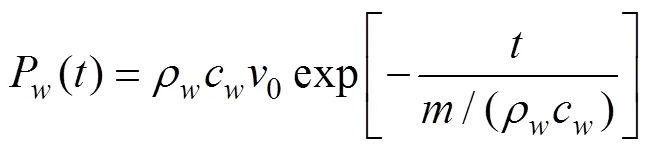
通过理论分析可知, 影响冲击波峰值压力与时间衰减系数的因素分别为撞击合速度与撞击比质量, 影响撞击合速度的因素为飞片的速度与质量及活塞的质量, 撞击比质量为量纲化之后的物理量, 当飞片与活塞面积相同时, 比质量仅与飞片和活塞的长度相关。可通过控制冲击波波形的影响因素调节冲击波波形, 得到所需的等效波形。

3 计算结果与分析

图2 当撞击合速度相同而比质量不同时压力时程曲线图

图3 当撞击合速度不同而比质量相同时压力时程曲线图

图4为水仓内=0处, 25种工况下由数值仿真计算所得载荷时间衰减系数随着撞击比质量变化规律与理论模型的对比情况。由图4得, 数值仿真结果与理论分析结果在撞击合速度与撞击比质量较低时吻合较好, 随着撞击合速度与撞击比质量的增加, 当飞片速度大于30 m/s时, 其时间衰减系数与理论值偏差较大, 这主要是因为, 在高速且飞片长度较长时, 在飞片与活塞撞击时发生较大程度的形变, 导致数值仿真结果与理论值相差较大; 当飞片长度较短时, 形变不明显, 对结果影响较小, 数值仿真结果与理论值吻合度较高。

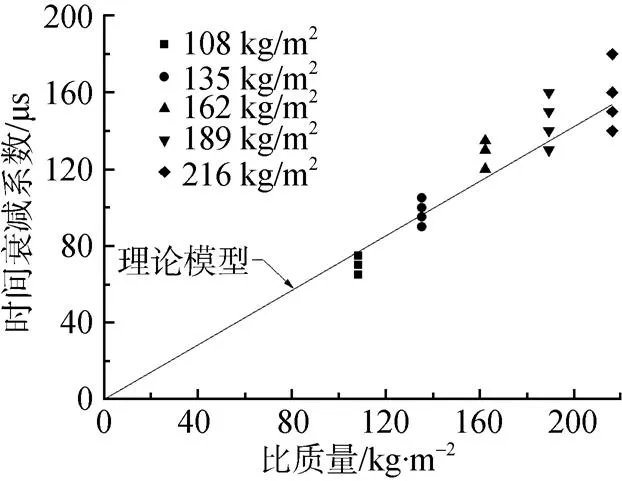
图4 载荷时间衰减系数随撞击比质量变化关系

图5为水仓内=0处, 25种工况下由数值仿真计算所得的载荷峰值压力随撞击合速度变化规律与理论模型的对比情况。由图5可得, 数值仿真结果与理论分析结果在撞击合速度与撞击比质量较低时吻合较好, 随着撞击合速度与撞击比质量的增加, 数值仿真结果与理论模型相差较大。同样是由于长杆飞片高速撞击导致的形变所致。由图4与图5分析可得, 在低速小质量撞击时, 数值仿真结果与理论模型有着较高的吻合度; 在大质量高速撞击时, 由于飞片与活塞的形变, 导致数值仿真结果与理论值相差较大。总体来看, 数值仿真结果与理论分析结果吻合较好, 可以通过调节撞击合速度与撞击比质量来调节由撞击产生的冲击波的波峰值压力与时间衰减系数, 以达到等效水下爆炸冲击波的目的。

图5 载荷峰值压力随撞击合速度变化关系

4 结论

本文针对传统方法中存在的问题, 提出了一种新的水下爆炸冲击等效加载实验方法, 通过飞片撞击的方式获得水下爆炸冲击等效载荷, 得出: 1) 由理论分析与仿真结果可知, 由撞击获得水下爆炸冲击等效载荷的实验方法有效, 可以通过调节撞击合速度与撞击比质量获得所需要的水下爆炸冲击载荷的等效载荷; 2)在撞击后飞片不发生大形变的前提下, 撞击产生冲击波的峰值压力仅与撞击合速度相关, 且基本呈线性关系; 3) 在撞击后飞片不发生大形变的前提下由撞击产生冲击波的时间衰减系数仅与撞击比质量相关, 且基本呈线性关系。

若采用该等效加载实验方法研究鱼雷爆炸对典型舰船的冲击响应, 需要进一步提高由撞击产生的冲击波的峰压值, 仍需对以下问题进行研究: 1) 改变飞片与活塞的材质, 选取大刚度材料, 从而提高飞片撞击速度以提高水仓内冲击波峰压值; 2) 在不影响实验效果的前提下降低活塞质量, 以减少活塞质量对撞击合速度的影响, 从而加大撞击合速度, 提高水仓内冲击波峰压值。

[1] Xue Z Y, Hutchinson J W. Crush Dynamics of Square Ho- neycomb Sandwich Cores[J]. International Journal for Numerical Methods in Engneering, 2006(65):2221-2245.

[2] Vaziri A, Xue Z, Hutchinson J W. Metal Sand Wich Plates with Polymeric Foam-filled Cores[J]. Mechanics of Mat- erials and Structures, 2006, 1(1): 95-128.

[3] Tilbrook M T, Radford D D, Fleck N A. Dynamic Crushing of Sandwich Panels with Prismatic Lattice Cores[J]. International Journal of Solids and Structures, 2007, 44 (18): 6101-6123.

[4] Radford D D, Deshpande V S, Fleck N A. The Use of Me- tal Foam Projectiles to Simulate Shock Loading on a Stru- cture[J]. International Journal of Impact Engineering, 2005, 31(9): 1152-1171.

[5] Espinosa H D, Lee S, Moldovan N. A Novel Fluid Structure Interaction Experiment to Investigate of Deforma­tion of Structural Elements Subjected to Impulsive Loading[J]. Experimental Mechanics, 2006, 46(6): 805-824.

[6] 项大林, 荣吉利, 胡长华. 一种撞击等效水下爆炸冲击加载实验测试装置系统: 中国, 201002665714.0[P]. 2012-12-05.

[7] Zamyshlyayev B V. Dynamic Loads in Underwater Expl- osion. AD-757183[P], 1973.

[8] 库尔. 水下爆炸[M]. 罗耀杰, 译. 北京: 国防工业出版社, 1960.

[9] Despande V S, Heaver A. Fleck N A. An Underwater Sho- ck Simulator[J]. Proceedings A of the Royal Society, 2006, 462(2067): 1021-1041.

(责任编辑: 杨力军)

An Equivalent Loading Method for Underwater Explosion Impact Experiment

YANG Yi-fang,GUO Rui,LIU Meng-meng,LIU Rong-zhong

(1. Ministerial Key Laboratory of ZNDY, Nanjing University of Science & Technology, Nanjing 210094, China; 2. Yu Xi Industrial Group Co.Ltd, Nanyang 473000, China)

An equivalent loading method for laboratory simulation is put forward to solve the problems in existing experimental studies of underwater explosion impact response. In the new method, flyer impact is adopted to achieve the equivalentload of underwater explosion. An equivalent theoretical model is established, and its analysis result is compared with that of the fluid-solid coupling numerical simulation. The comparison shows that both results agree well. By using this theoretical model, the required equivalent load for different underwater explosion impact can be achieved by adjusting the flyer′s impact velocity and specific mass of impact. This study may provide a new idea for research on torpedo explosion impact response of typical ship structure.

underwater explosion; equivalent loading; impact response; fluid-solid coupling

TJ630.1; O383

A

1673-1948(2014)05-0357-04

2014-06-06;

2014-06-26.

高等学校博士学科点专项科研基金(20133219110019).

杨一方(1990-), 男, 硕士, 主要研究方向为冲击动力学.