钛基复合材料压气机叶环应力的数值模拟

张红园，杨延清，罗贤，黄斌，裴会平

(1.西北工业大学凝固技术国家重点实验室，陕西西安710072；2.中国燃气涡轮研究院，四川成都610500)

钛基复合材料压气机叶环应力的数值模拟

张红园1，杨延清1，罗贤1，黄斌1，裴会平2

(1.西北工业大学凝固技术国家重点实验室，陕西西安710072；2.中国燃气涡轮研究院，四川成都610500)

采用有限元分析方法，建立三维循环对称模型，对连续SiC纤维增强钛基复合材料压气机叶环的应力进行了研究。考虑周围基体包套和中心复合材料的热残余应力，重点分析了叶环尺寸、温度及基体材料性能对叶环应力分布的影响。结果表明，当叶环直径较小、工作温度较低时，叶环的最大环向应力点在内径；随着直径增大、工作温度升高，最大环向应力点出现在中心复合材料靠近内径一侧。基体材料的弹性模量、热膨胀系数和密度，对叶环的应力分布有重要影响，应尽量选择密度低、弹性模量和热膨胀系数较大的钛合金作为基体材料。

钛基复合材料；压气机叶环；应力；有限元模拟；热残余应力

1 引言

新一代高推重比航空发动机需要轻质、高强度材料的支撑。连续SiC纤维增强钛基复合材料(TMC)，由于沿纤维方向具有高的比强度和比刚度，在600～1 000℃仍可保持较好的抗疲劳和蠕变性能，在发动机压气机转子部件中具有重要的应用前景。相比传统的镍、钛合金压气机转子，TMC制备的压气机叶环可减重高达50%，而这一设计也被誉为航空发动机革命性的突破[1-4]。

相对于传统金属材料，TMC具有各向异性及不同失效模式。因此从安全角度考虑，TMC叶环在先进航空发动机压气机中的潜在优势发挥之前，必须对其力学分析方法等进行预先论证。对于压气机转子，叶环高速旋转时产生的惯性力对叶环的破坏是个突出问题，因此准确预测叶环在工作状态下的应力分布对其安全性至关重要。以前，人们对TMC的研究主要集中在界面反应、力学性能及细观有限元等方面，对TMC制备的大型结构件的研究鲜有报道。Arnold等[5]应用有限元分析软件MARC，对亚尺寸TMC叶环的爆破强度及疲劳寿命进行了预测。研究中，通过在叶环内径表面施加均匀压力，以产生径向压应力和环向拉应力。结果表明，在427℃叶环能承受的极限压力为221 MPa，起始破坏点在中心复合材料靠近内径一侧。Robinson等[6]应用各向异性塑性理论，计算得到叶环内径表面承受均匀压力的极限值范围为172～200 MPa。但上述研究中，均是在叶环内径施加均匀压力以产生环向拉伸应力，而实际上叶环的环向应力是其高速旋转时离心力所致。Natsumura等[7]采用数值模拟与旋转实验相结合的方法，研究了TMC叶环的失效模式与机制，表明叶环失效主要是由于环向过载所致。

本文利用有限元方法，建立三维循环对称模型，对TMC叶环的应力分布进行探讨，分析叶环的尺寸、温度及基体材料参数变化对应力分布的影响，以期为TMC叶环结构设计、材料选择提供一定依据。

2 有限元模型

2.1 叶环宏观模型

有限元分析通过ANSYS实现。根据叶环的循环对称性，取其1/20建立3D有限元模型，如图1所示。模型由中心复合材料SiCf/Ti-6Al-4V和周围基体包套Ti-6Al-4V组成，叶环横截面50 mm×40 mm(轴向厚度40 mm)，复合材料增强面积为30 mm×20 mm。边界条件设置如下：在x等于内径、z=0处，选取y=0°、9°、18°的三个节点，约束其z向位移，同时为避免刚体位移，上述所有节点的y向位移也被约束；两个周期对称面内(即y=0°和y=18°处的平面)对应的节点，在x、y、z所有方向上具有相同位移。上述提到的坐标系为整体柱坐标系。周围基体包套和中心复合材料，分别采用三维单元SOLID45和SOLID186。加载角速度为14 320 r/min。

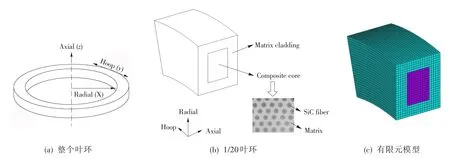
图1 TMC叶环有限元模型Fig.1 Finite element model of TMC ring

假设周围基体包套和中心复合材料在热等静压过程中结合良好。分析过程中，考虑从固化温度冷却过程中，周围基体包套和中心复合材料由于热膨胀系数(CTEs)不匹配引起的热残余应力。参考温度设定在700℃，在700℃以上，认为周围基体包套和中心复合材料不产生热残余应力[5]。模拟过程分为两个载荷步：第一载荷步计算热残余应力，第二载荷步计算高速旋转时由于离心作用产生的应力。自此，若没特别说明，文中提到的叶环应力分布，均为热残余应力和离心作用产生的应力的叠加。

为研究叶环尺寸对应力分布的影响，叶环横截面保持50 mm×40 mm不变，内径分别为200、300、400 mm。分析温度对叶环应力分布的影响时，叶环内径为400 mm，温度选择25℃、300℃、400℃、500℃。当研究基体材料参数变化对叶环应力分布的影响时，内径为400 mm，采用控制变量的方法，依次探讨基体弹性模量、热膨胀系数及密度对应力的影响。

周围基体包套看作各向同性，理想弹塑性材料，服从Von Mises屈服准则，其性能见文献[8]。中心复合材料看作横观各向同性材料，采用Hill各向异性弹塑性本构[9]。采用Schapery[10]模型计算复合材料的纵向热膨胀系数，横向热膨胀系数通过局部混合定则[11]得到。

2.2 细观力学有限元计算复合材料的有效弹性常数

中心复合材料看作横观各向同性材料，而横观各向同性材料为正交各向异性的特例，有五个独立弹性常数。由于通过实验得到的复合材料与温度相关的弹性常数有限，故根据复合材料中纤维排布的周期性，建立代表性体积单元(RVE)有限元模型计算复合材料的有效弹性常数。模型中考虑了纤维排布方式及界面相的影响。TMC中常见的纤维排布有四方和六方排布，示意图见图2，RVE的有限元模型见图3。在单独的正向载荷作用下，考虑到RVE几何尺寸和载荷形式的对称性，建模时选取其1/4，模型尺寸沿x、y、z三个方向分别为a、b、c；在纵向剪切模型中，模型尺寸沿x、y、z三个方向分别为a1、2b、2c(四方和六方排布中的a、b、c取值不同)。不同载荷下，RVE的边界条件设置见表1，其中u，v，w分别表示沿x、y、z方向的位移。对于SiCf/Ti-6Al-4V复合材料，SiC纤维直径为100 μm，纤维体积分数为35%，纤维表面涂C为3 μm厚，热等静压后，反应层主要产物TiC约为1 μm厚[12]，故残留的C涂层为2 μm厚。SiC纤维、C及TiC的材料性能见文献[8]和[12]。基于应变能平衡理论，通过高斯定理，由RVE中非均匀的应力、应变场计算出RVE中的平均应力和应变，从而计算复合材料弹性常数，具体算法见文献[13]。由于叶环经热等静压后纤维不可能完全是四方或六方排布，故复合材料参数取纤维四方和六方排布模型计算得到的平均值，具体参数见表2。

图2 纤维四方排布和六方排布示意图Fig.2 The schematic diagram for square and hexagonal array of the fiber

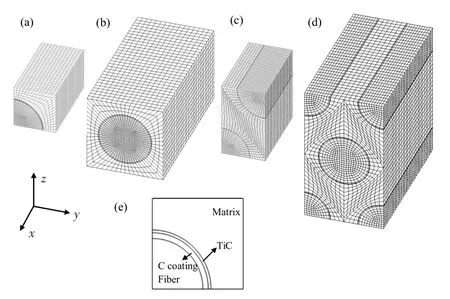
图3 不同载荷下纤维四方和六方排布的有限元模型Fig.3 Finite element model of square array and hexagonal array under different loading

表1 不同载荷下代表性体积单元的边界约束条件Table 1 Boundary conditions of a reprasentative volume element under different loading

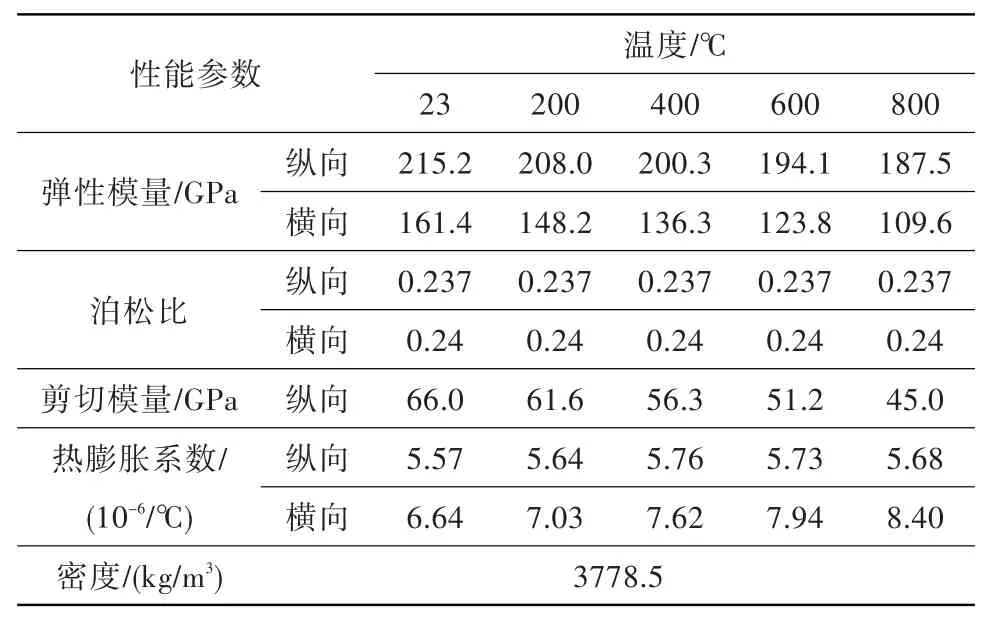
表2 SiCf/Ti-6Al-4V复合材料性能Table 2 The properties of SiCf/Ti-6Al-4V composites

3 模拟结果与分析

图4为TMC叶环内径为400 mm时，400℃下沿径向、环向、轴向的应力和等效应力云图。结果显示，在径向和轴向上，中心复合材料为压应力，周围基体包套为拉应力。这主要是因为在径向和轴向上离心力产生的应力很小，其应力主要是热残余应力所致。当TMC叶环从固化温度冷却后，由于周围基体包套与中心复合材料的热膨胀系数不匹配产生热残余应力，而周围基体包套的热膨胀系数大于中心复合材料，故冷却过程中，周围基体包套产生拉应力，中心复合材料产生压应力。环向应力为拉伸状态，最大值位于叶环中心复合材料靠近内径一侧，约为711 MPa，这也是采用TMC叶环所期望达到的效果，随后沿径向逐渐减小。基体包套的最大环向应力约为477 MPa，未达到屈服极限，处于安全范围。等效应力为径向、环向和轴向应力的综合作用，其分布趋势与环向应力相同，大小与环向应力接近。环向应力比径向和轴向的应力高很多，在叶环变形中起到了非常重要的作用。因此，以下应力分析，均基于已定义路径(y=0°且z=20)的环向应力，路径如图4 (b)中箭头所示。

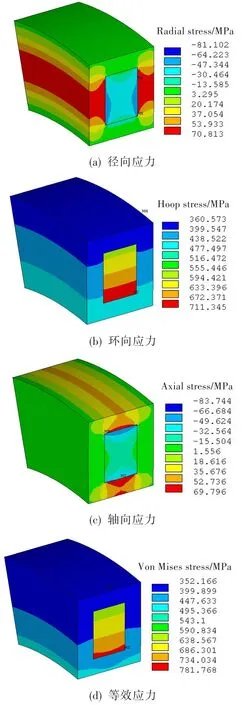
图4 400℃时TMC叶环应力及等效应力分布Fig.4 The stress and Von Mises stress distribution of TMC ring at 400℃

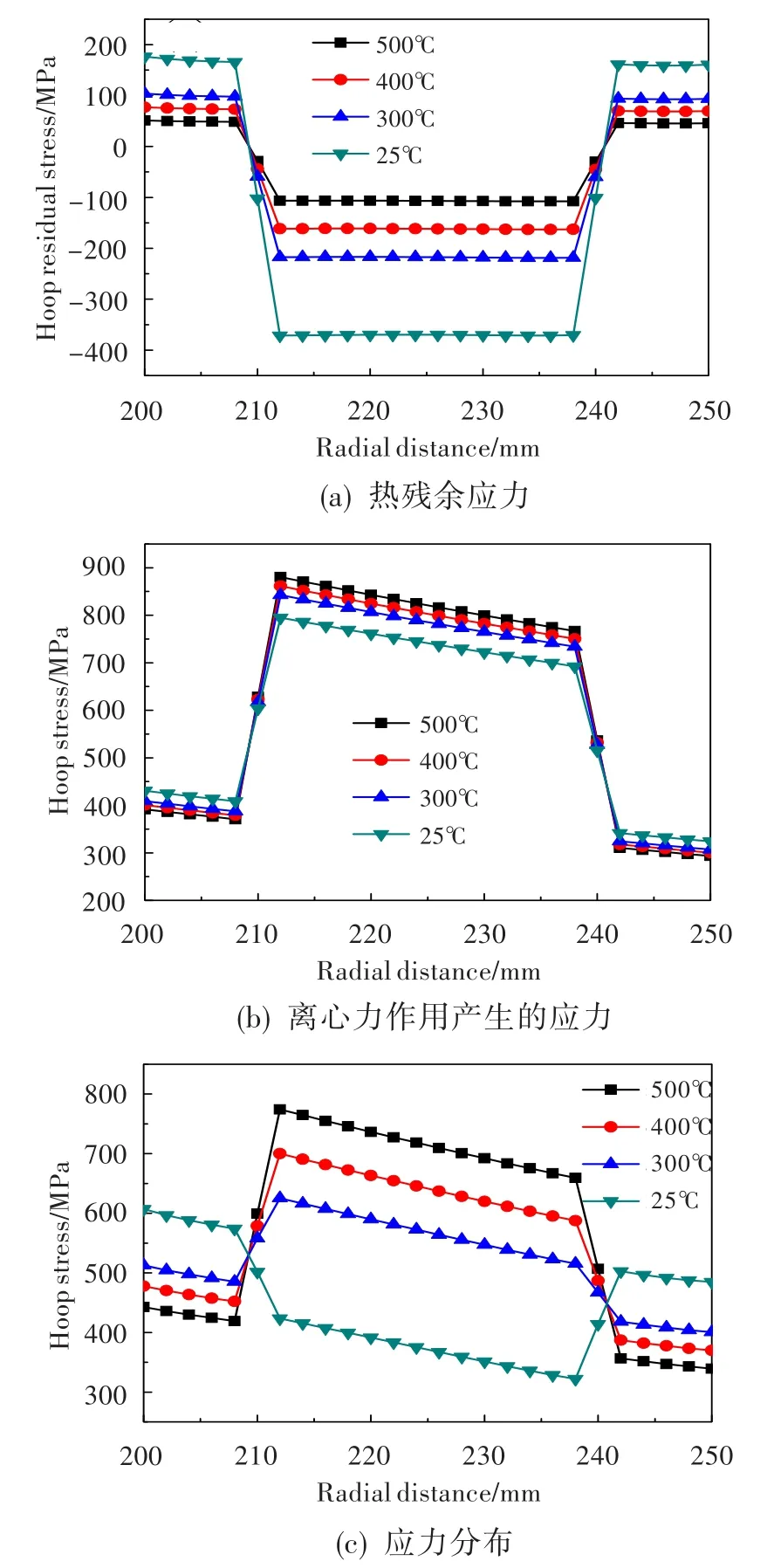
图5 不同温度下TMC叶环的应力分布Fig.5 Stress distribution of TMC ring at different temperatures

3.1 温度对应力分布的影响

压气机叶环在不同温度下的环向应力如图5所示。从图5(a)中可看出，随着温度的升高，热残余应力逐渐减小。25℃时复合材料、周围基体包套中的热残余应力分别为-370 MPa和170 MPa左右，500℃时两者分别降低到-100 MPa和50 MPa左右。这主要是因为随着温度的升高，一部分热残余应力得到了释放。14 320 r/min转速下，离心力作用产生的最大环向应力均出现在复合材料靠近内径一侧。随着温度的升高，由于基体弹性模量严重下降，周围基体包套承担的应力减小，中心复合材料的应力增大。25℃时基体包套和复合材料的最大应力分别为430 MPa、805 MPa，500℃时两者分别为390 MPa和890 MPa，如图5(b)所示。综合考虑热残余应力和离心力作用时，最大环向应力位置随温度不同而改变，见图5(c)。25℃时最大环向应力607 MPa在叶环内径，300℃时环向应力在中心复合材料靠近内径一侧达到峰值625 MPa。随着温度的继续升高，中心复合材料的环向应力增大，周围基体包套的环向应力减小。由此可得出，综合考虑热残余应力和离心力作用时，最大环向应力出现位置，与某一温度下周围基体包套和中心复合材料由于离心力产生的最大应力梯度及热残余应力梯度有关。若周围基体包套和中心复合材料由于离心力产生的最大应力梯度大于热残余应力梯度，则最大应力点在中心复合材料靠近内径一侧；反之，最大应力点在叶环内径处。

从温度对TMC叶环应力分布的影响可看出，25℃时最大应力点在叶环内径，这并不是使用TMC叶环所期望达到的效果。一般情况下，压气机工作温度高于室温，在300℃、400℃和500℃下，叶环应力分布趋势相同，只是大小有所不同，因此下面的应力分析中选定中间温度400℃。

3.2 叶环尺寸对应力分布的影响

400℃时不同直径TMC叶环的环向应力分布如图6所示。可见，不同直径叶环的热残余应力基本相同，周围基体包套、中心复合材料的热残余应力分别为70 MPa和-160 MPa左右。即只要叶环横截面保持不变，内外径变化对热残余应力没有影响。这主要是因为中心复合材料和周围基体包套的体积百分数不变。14 320 r/min转速下，离心力产生的最大环向应力点，均出现在复合材料靠近内径一侧。随着叶环直径的增大，环向应力随之增大。当叶环内径为200 mm时，基体包套、复合材料的最大应力分别为140 MPa和285 MPa；当内径增大到400 mm时，基体包套、复合材料的最大应力分别增大至400 MPa和871 MPa。且周围基体包套和中间复合材料应力梯度，随着叶环直径的增大而增大，见图6(b)。综合考虑热残余应力和离心力作用时，随着叶环直径的增大，环向应力随之增大，但最大环向应力点出现位置随直径不同而变化。当内径为200 mm时，最大应力点在叶环内径，为220 MPa；当内径为300 mm和400 mm时，最大应力点在中心复合材料靠近内径一侧，分别为370 MPa和700 MPa，如图6(c)所示。由此可得出，叶环直径对应力分布的影响与温度对应力分布的影响类似。

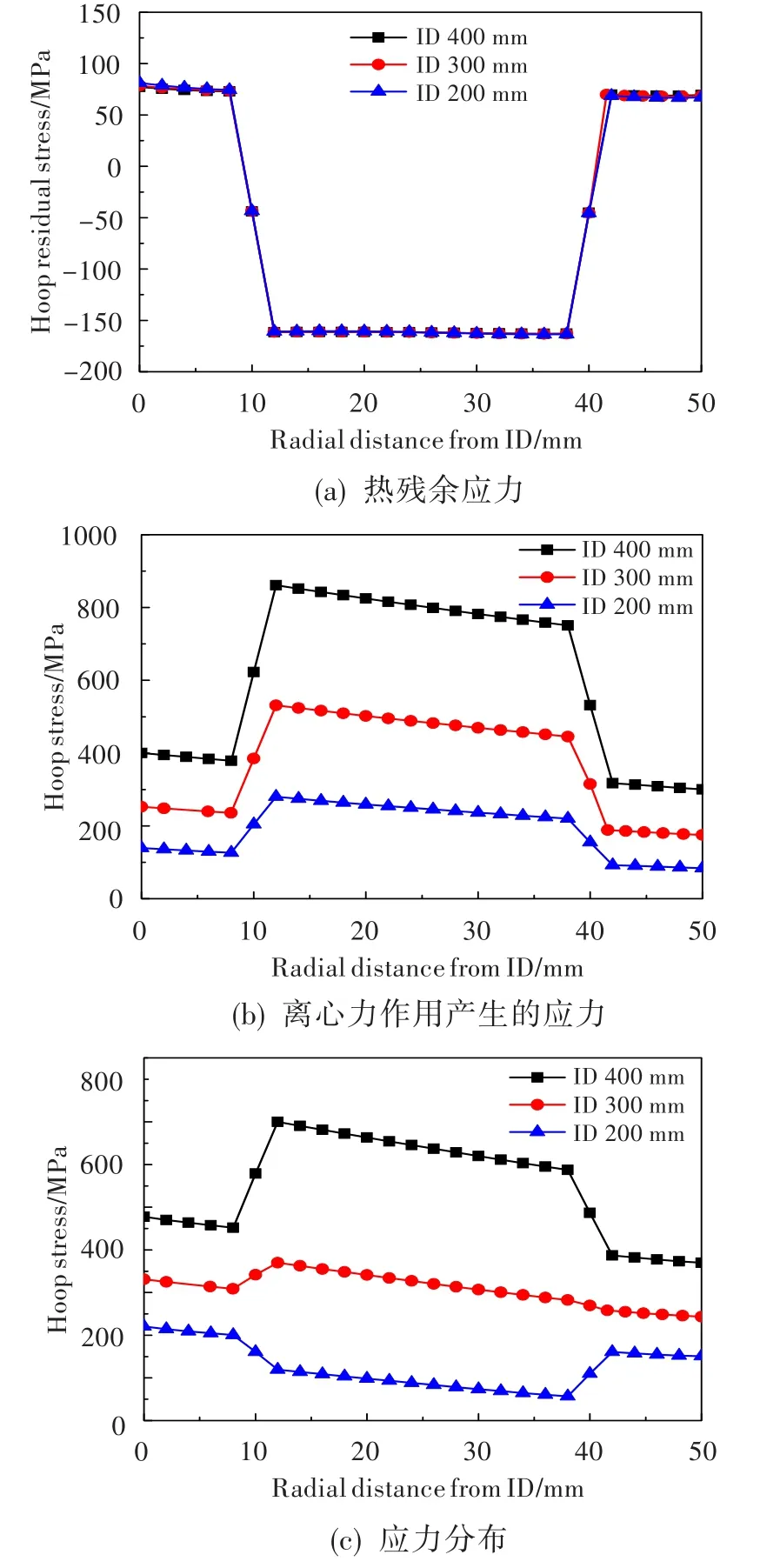
图6 不同直径下TMC叶环的应力分布Fig.6 Stress distribution of TMC ring of different diameters

3.3 基体材料参数变化对应力分布的影响

根据有限元模拟结果，叶环应力分布与基体材料的弹性模量、热膨胀系数及密度等材料属性有关。因此，本节选取叶环内径基体包套的最大环向应力点P1，和中心复合材料靠近内径一侧的最大环向应力点P2，考察两点在400℃时的应力随基体材料参数的变化规律。

为研究基体弹性模量和热膨胀系数对叶环应力分布的影响，以Ti-6Al-4V的弹性模量和热膨胀系数为基准1，横坐标中引入一虚拟放大因子来表示基体弹性模量和热膨胀系数的变化。基体弹性模量对应力的影响如图7(a)所示。可见，随着基体材料弹性模量的增大，叶环内径处基体包套的最大应力升高，中心复合材料靠近内径一侧的最大应力下降。其主要原因为：随着基体弹性模量的升高，热残余应力增大，见图7(b)；另外，14 320 r/min转速下，随着基体弹性模量的增大，周围基体包套由于离心作用产生的应力增大，而中心复合材料由于离心力作用产生的应力减小，如图7(c)所示。

图8(a)为基体热膨胀系数变化对叶环应力分布的影响。可见，随着基体热膨胀系数的增大，叶环内径处基体包套的最大应力升高，而中心复合材料靠近内径一侧的最大应力下降，与弹性模量对应力分布的影响趋势相同。在14 320 r/min转速下，热膨胀系数变化对离心力作用产生的应力没有影响，这主要是由于随着基体热膨胀系数的增大，周围基体包套和中心复合材料的热膨胀系数差异增大，从固化温度冷却过程中两者的不匹配程度增加，热残余应力增大所致，如图8(b)所示。

图7 基体弹性模量对TMC叶环应力分布的影响Fig.7 The influence of elastic modulus of matrix on the stress distribution of TMC ring

图8 基体热膨胀系数对TMC叶环应力分布的影响Fig.8 The influence of coefficients of thermal expansions of matrix on the stress distribution of TMC ring

基体密度变化对叶环应力分布的影响如图9(a)所示。可见，随着密度的增大，叶环内径处基体包套的最大应力和中心复合材料靠近内径一侧的最大应力均有增大趋势，且中心复合材料的增大趋势更为明显。基体密度变化不会对热残余应力产生影响，这主要是由于基体密度增大，旋转时由离心力作用产生的应力增大所致，见图9(b)。

图10为Ti-24Al-11Nb和super α2两种基体增强的TMC叶环在400℃下的环向应力分布，其中两种材料的性能见文献[14]。与图4(b)比较可以看出，Ti-6Al-4V、Ti-24Al-11Nb和super α2增强的TMC叶环，其中心复合材料靠近内径一侧的最大应力逐渐减小，分别为711 MPa、612 MPa和574 MPa，内径处基体包套的最大应力逐渐增大，依次为477 MPa、493 MPa和504 MPa。这主要是三种基体材料的弹性模量、热膨胀系数和密度综合作用的结果。首先，三者之间热膨胀系数相差无几，其影响可忽略。其次，从密度方面考虑，Ti-6Al-4V的密度为4.44 kg/m3，而Ti-24Al-11Nb和super α2的密度均为4.20 kg/m3。从图9(a)中可知，当密度在4.20～4.44 kg/m3范围变化时，中心复合材料、基体包套的最大应力值变化幅度分别为37 MPa和17 MPa。最后，考虑弹性模量的影响。上述三种材料室温下的弹性模量差别不大，但super α2作为金属间化合物，其高温下的弹性模量远高于另外两种，850℃时super α2的弹性模量依然高达104 GPa。结合图7(a)可知，super α2增强的TMC叶环中心复合材料的最大应力在三者中最小，而基体包套的最大应力最大。由于Ti-6Al-4V密度大于Ti-24Al-11Nb，且弹性模量略小于后者，故Ti-6Al-4V增强的TMC叶环中心复合材料部分最大应力值在三者中最高，为711 MPa。

在基体钛合金包套的最大应力不超过其屈服强度的前提下，应重点关注中心复合材料的最大应力值，故选择基体材料时，应尽量选密度低、弹性模量和热膨胀系数较大的钛合金。但是在弹性模量和热膨胀系数增大时，虽然中心复合材料的最大应力减小，但基体包套的最大应力增大，故基体的弹性模量和热膨胀系数不可过大，以免基体包套部分的最大应力超过其屈服强度，出现塑性变形。

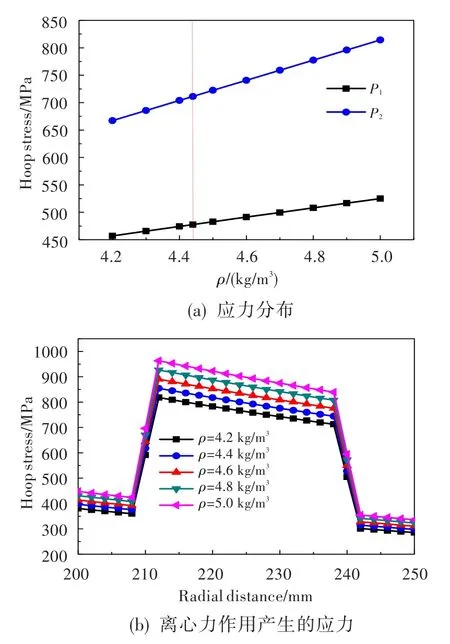
图9 基体密度对TMC叶环应力分布的影响Fig.9 The influence of density of matrix on the stress distribution of TMC ring

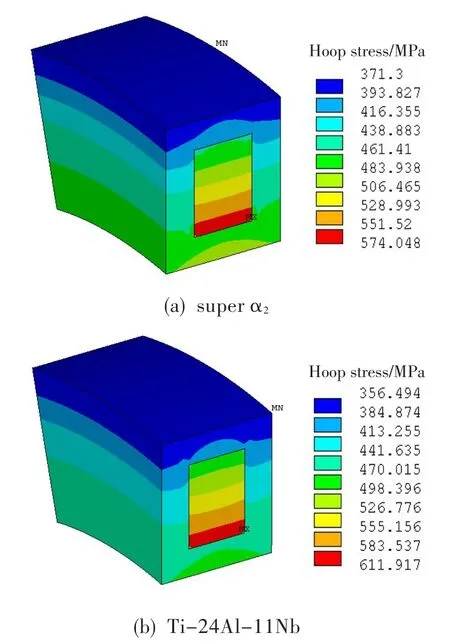
图10 不同基体材料TMC叶环的环向应力分布Fig.10 The hoop stress distribution of TMC ring of different matrix materials

4 结论

(1)叶环内径保持在400 mm，在25℃时，周围基体包套和中心复合材料由于离心力产生的最大应力梯度为375 MPa，小于两者之间的热残余应力梯度(540 MPa)，最大环向应力点在叶环内径。随着温度的升高，周围基体包套和中心复合材料由于离心力产生的最大应力梯度增大，热残余应力梯度减小，最大环向应力出现在中心复合材料靠近内径一侧。

(2)温度保持在400℃，当内径为200 mm时，周围基体包套和中心复合材料由于离心力产生的最大应力梯度小于热残余应力梯度，最大环向应力点在叶环内径。随着直径增大，周围基体包套和中心复合材料的最大离心力梯度增大，热残余应力梯度不变，最大环向应力点在中心复合材料靠近内径一侧。

(3)随着基体材料弹性模量和热膨胀系数的增大，叶环中心复合材料靠近内径一侧的最大环向应力下降；随着基体密度的增大，中心复合材料靠近内径一侧的最大环向应力增大。因此，应尽量选择密度低、弹性模量和热膨胀系数较大的钛合金作为基体材料。

[1]Hooker J A，Doorbar P J.Metal Matrix Composites for Aeroengines[J].Materials Science and Technology，2000，16(7-8)：725—731.

[2]杨延清，朱艳，陈彦，等.SiC纤维Ti基复合材料的制备及性能[J].稀有金属材料与工程，2002，31(3)：201—204.

[3]Carrere N，Valle R，Bretheau T，et al.Multiscale Analysis of the Transverse Properties of Ti-Based Matrix Compos⁃ites Reinforced by SiC Fibres:From the Grain Scale to the Macroscopicscale[J].International Jounal of Plasticity，2004，20(4)：783—810.

[4]Leyens C，Hausmann J，Kumpfert J.Continuous Fiber Re⁃inforced Titanium Matrix Composites:Fabrication,Proper⁃ties and Applications[J].Advanced Engineering Materials，2003，5(6)：399—410.

[5]Arnold S M,Wilt T E.Deformation and Life Prediction of Circumferentially Reinforced SCS-6/Ti-15-3 Ring[C]//. Zaretsky E V.MMC Life System Development(Phase I)-A NASA/Pratt&Whitney Life Prediction Cooperative Pro⁃gram.NASA RP-1361，1996.

[6]Robinson D N，Pastor M S.Limit Pressure of a Circumfer⁃entially Reinforced SiC/Ti Ring[J].Composites Engineer⁃ing，1992，2(4)：229—238.

[7]Natsumura T，Nojima Y，Suzumura N，et al.Component Design of CMC and MMC Rotor for Turbine Engine Appli⁃cations[C]//.31st International SAMPE Technical Confer⁃ence.1999：130—141.

[8]Ma Z J，Yang Y Q，Lü X H，et al.The Effect of Matrix Creep Property on the Consolidation Process of SiC/ Ti-6Al-4V Composite[J].Materials Science and Engineer⁃ing:A，2006，433(1)：343—346.

[9]Hill R.The Mathematical Theory of Plasticity[M].Oxford：Oxford university press，1998.

[10]Schapery R A.Thermal Expansion Coefficients of Compos⁃ite Materials Based on Energy Principles[J].Journal of Composite Materials，1968，2(3)：380—404.

[11]黄斌.SiCf/Ti基复合材料的界面及组织性能研究[D].西安：西北工业大学，2010.

[12]Huang B，Yang Y Q，Luo H J，et al.Effects of the Coating System and Interfacial Region Thickness on the Thermal Residual Stresses in SiCf/Ti–6Al–4V Composites[J].Ma⁃terials and Design，2009，30(3)：718—722.

[13]Sun C T，Vaidya R S.Prediction of Composite Properties from a Representative Volume Element[J].Composites Sci⁃ence and Technology，1996，56(2)：171—179.

[14]Boyer R，Welsch G，Collings E W.Materials Properties Handbook:Titanium Alloys[M].Ohio：ASM Internation⁃al，1994.

Numerical Simulation on Stress Distribution of Ti-Matrix Composite Ring

ZHANG Hong-yuan1，YANG Yan-qing1，LUO Xian1，HUANG Bin1，PEI Hui-ping2
(1.State Key Lab of Solidification Processing，Northwestern Polytechnical University，Xi’an 710072，China；2.China Gas Turbine Establishment，Chengdu 610500，China)

A three-dimensional cyclic symmetry finite element model was developed to investigate the stress distribution of compressor ring which was fabricated by continuous SiC fiber reinforced titanium-ma⁃trix composites(TMC).The effects of size of the ring,temperature and properties of the matrix material on the stress distribution were analyzed emphatically when taking thermal residual stresses between matrix cladding and composite core into consideration.The results indicate that when the diameter of TMC ring is smaller and working temperature is lower,the hoop stresses have a maximum value at the inner diameter (ID)of the ring;as the diameter of the ring and working temperature increase,the hoop stresses reach a peak value at the ID of composite core.The elastic modulus,coefficients of thermal expansions(CTEs)and density of matrix material have a significant effect on the stress distribution of TMC ring.Low density,rela⁃tively high elastic modulus and CTEs titanium alloy should be selected as the preferable matrix material.

titanium-matrix composites(TMC)；compressor bling；stress；finite element analysis；thermal residual stress

V257

：A

：1672-2620(2014)06-0041-08

2014-01-08；

：2014-09-25

国家自然科学基金(51271147，51201134，51201135)

张红园(1987-)，女，河北保定人，硕士研究生，主要从事钛基复合材料应力研究。