利用几何、算术均值不等式证明有关数学问题的技巧

王洁琼

（汉中职业技术学院，陕西 汉中 723000）

【学法指导】

利用几何、算术均值不等式证明有关数学问题的技巧

王洁琼

（汉中职业技术学院，陕西 汉中 723000）

巧用几何、算术均值不等式证明某些有关正整数的数学问题时，往往可使问题变难为易，化繁为简，达到事半功倍的效果，同时享受数学的简洁美。本文通过对若干数学问题的证明，体现了几何、算术均值不等式在证明有关正整数的数学问题的技巧。

几何平均数；算术平均数；均值不等式

几何、算术均值不等式是指n个正数a1，a2，…，an的几何平均数与算术平均数满足

其中当且仅当a1=a2=a3=…=an时等号成立。

在证明某些有关正整数n的数学问题时，若能巧用几何、算术均值不等式，可以使问题变难为易，化繁为简。本文将举例说明。

例1 设k，n∈N+，且k＜n，求证

例2 设n∈N+，且N≥2，求证

例3 已知x＞-1，x≠0，n∈N+，且N≥2，求证

（1+x）n＞1+nx

这是著名的伯努利不等式，它的应用广泛，书中大多采用数学归纳法证明，虽然思路清晰，推理自然，但步骤较长，格式较繁，若能巧用几何、算术均值不等式则会简单得多。

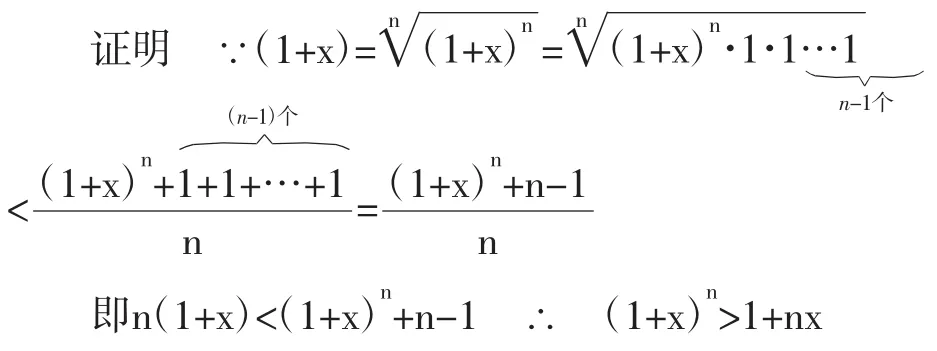
小结：由以上例子可以看出，公式的巧用，问题的妙解，变难为易，化繁为简，使人赏心悦目，达到事半功倍的效果，同时享受到数学的简洁美。

G642.4

A

1674-9324（2014）42-0224-02

王洁琼（1985-），女，陕西洋县人，硕士研究生，助教，研究方向：数学教育。