复杂可修系统可靠性维修性仿真研究

林王鹏，孙武军



复杂可修系统可靠性维修性仿真研究

林王鹏，孙武军

（海军 91640 部队，广东湛江 524064）

对于大型复杂可修系统，常规的解析法已经难以得到想要的结果，本文研究用基于故障树最小割集和维修的数学仿真模型来对系统的可靠性和维修性进行分析计算，结果表明仿真合理，对系统可靠性估计和维修决策有一定的指导价值。

大型复杂可修系统 最小割集 故障树 数学仿真

0 引言

1 模型建立

1.1 系统组成

设复杂可修系统由n个子系统或部件组成，则

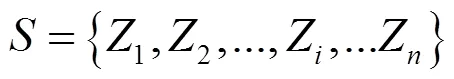
1.2 最小割集故障时间和维修时间的抽样方法

这里的抽样是建立在蒙特卡罗思想的基础上。蒙特卡罗方法的核心是大数定律，当求解问题为概率时，可以通过大量抽样试验得到这种事件出现的频率，以频率代替概率。本文抽样都是用的MATLAB自带的随机数发射器直接获得，虽然结果会有一定的波动，但是在大量事件时结果在允许的误差范围内。

1.3 系统逻辑关系

1）致命性故障的识别

设系统持续时间为T，满足式(1)发生致命性故障。

式中T为持续工作时间，1j为第j个割集第一次故障时间。

2）致命性故障修复状态的识别。

当满足式（2）时表示系统致命性故障修复。

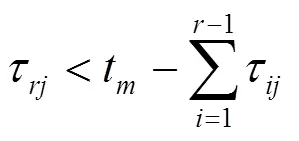
式中：τ为第j割集第r次故障的修复时间，t为允许修复时间，r为故障次数。

3）修复后割集（部件）正常工作的识别

2 仿真流程

1）基本数据的获取

主要包括所有底事件的故障概率分布函数和维修概率分布函数、总仿真次数NS及任务时间T等。

2）通过仿真次数判断仿真是否结束，如果仿真次数L>NS，仿真结束，转至（5）；否则，仿真继续进行。

5）整理统计量输出。

任务成功次数：

任务失败次数

任务成功概率

平均修复时间

平均故障间隔时间

3 仿真实例

图1 拦截弹任务失败的故障树

由图1看得，拦截弹是串联结构，每个底事件是系统失效的最小割集。

表2数据符合实际任务使用时的趋势，即当任务持续时间越短，故障率越低，任务成功率越高，武器装备的所需的维护保养越少。

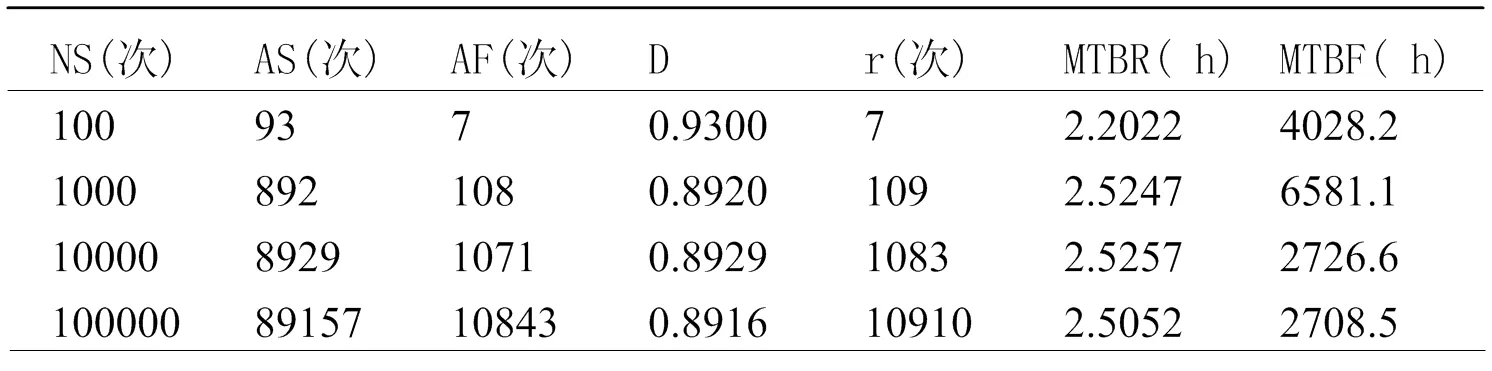
下面研究模拟次数对模型准确度的影响。设T=30时，模拟次数NS从100递增至100000时的数据表如表3所示。

从各项数据可以看出，仿真次数NS越大，仿真精度越高，但是当NS=10000后精度趋于稳定，在下面的分析中用NS=10000时的数据。

当NS=10000时表2与表3数据有细小的变化，这是由于本文随机数是利用MATLAB随机数产生器产生，分布模型随机抽样有波动，但是作为大规模抽样对结果影响不大，都在误差范围内。

表1 拦截弹各分系统失效分布类型及参数

表2T取不同值时输出对比表

表3 NS取不同值时输出对比情况

4 结论

本文研究了大型复杂可修系统基于故障树割集和维修的数学仿真方法，用到了蒙特卡罗抽样方法，仿真结果表明仿真合理，贴近工程实际，有很好的应用性，对大型复杂可修系统的可靠性管理决策有很大的指导价值。

[1] 杨宇航, 冯允成．复杂可修系统可靠性维修性综合仿真研究［Ｊ］．系统仿真学报, 2002, 14(8): 978-983.

[2] 王武宏, 孙逢春, 李晓雷．复杂可修系统可信度的数学仿真方法［Ｊ］．系统工程理论与实践, 2001, 7: 110-114.

[3] 杨为民, 盛一兴, 等. 系统可靠性数学仿真[M]. 北京: 航空航天大学出版社.1990.

[4] 廖武, 张诤敏, 陈云翔等．作战飞机可靠性与维修性仿真模型［Ｊ］．火力与指挥控制, 2005, 30(7): 51-58.

[5] 邵延峰, 薛红军, 基于故障树的可靠性数学仿真方法研究, 机械强度, 2008, 30（3）: 381-385.

Simulation of Reliability and Maintainability of Complex Repairable System

Lin Wangpeng, Sun Wujun

(91640 Navy Troop, Zhanjiang 524064, Guangdong, China)

TP277

A

1003-4862（2014）08-0021-03

2014-01-06

林王鹏（1976-），男，工程师。研究方向：军械保障。