拟Bent函数的代数免疫性

刘志高

马鞍山职业技术学院，安徽 马鞍山 243031

0 引 言

布尔函数作为序列密码、分组密码和Hash函数的重要组件，其密码学性质的好坏直接影响到密码系统的安全性. 文献[1]提出了一类密码学性质优良的函数——拟Bent函数, 它是包含Bent函数和部分Bent函数的更大的函数类, 可以具有Bent 函数所不具有的密码学性质, 如: 平衡性、相关免疫性, 能有效抵抗线性攻击、相关攻击和差分攻击等. 随后, 人们相继研究了拟Bent函数的一些构造方法及其非线性度、代数次数、相关免疫性、扩散性、正规性、对偶性等密码学指标[2-6]. 研究表明, 拟Bent 函数的密码学性质优良, 在密码设计及通信领域中有广泛的应用.

随着密码技术的不断发展, 各种新兴的攻击方法相继出现. 尤其是代数攻击[7]的出现, 在密码学界引起轩然大波, 人们利用代数攻击成功地破译了Toyocrypt和LILI. 代数攻击对现有的密码体制形成了巨大威胁, 为抵抗代数攻击, Meier等人于2004年引入了度量布尔函数安全性的新指标——代数免疫性[8]. 代数免疫一经提出就受到密码学界的广泛关注, 研究成果主要集中在两方面: 一是最优代数免疫函数的构造方法研究[9-12]; 二是对已有的密码学性质良好的布尔函数的代数免疫性研究[13-15].关于代数免疫与其他密码学指标之间的关系已有少量的研究，如文献[16]研究了布尔函数的代数免疫与扩散阶之间的关系. 但是, 针对拟Bent函数的代数免疫性分析还未得到系统的成果, 探讨拟Bent函数是否存在低次零化子, 能否抵抗代数攻击, 具有很强的现实意义.

本文基于布尔函数非线性度与代数免疫度之间的关系, 利用Walsh谱、组合数等工具对拟Bent函数(包括偶数变元和奇数变元)的代数免疫性进行系统地分析, 得到了判定其存在低次零化子的一个充分条件. 该条件只需要根据拟Bent函数的阶数k与变元个数n之间的关系就可进行判定, 不需要利用Walsh循环谱或代数正规形来判定, 非常直观有效. 进一步, 还研究了如何根据拟Bent函数的阶数k与变元个数n之间的具体关系来确定其代数免疫度的上界.

1 预备知识

一个n元布尔函数f是指从GFn(2)={0,1}n到GF(2)={0,1}的一个映射. 记Bn为所有n元布尔函数组成的集合, 记An为所有n元仿射布尔函数的集合.

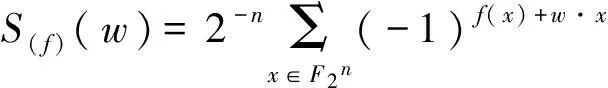
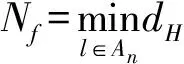
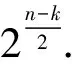
易知,n为偶数时, 0阶拟Bent函数就是Bent函,n阶拟Bent函数就是仿射函数.

定义4[7]设f∈Bn, 若∃0≠g∈Bn, 使得f·g=0恒成立, 则称g是f的零化子.

由于f·(1+f)=0, 因此f的零化子一定存在. 记f的全体零化子构成的集合为An(f).

定义5[8]设f∈Bn, 称f的零化子和1+f的零化子的代数次数的最小值为f的代数免疫度. 记作AI(f), 即AI(f)=min{deg(g)|g∈An(f)org∈An(1+f)}.

2 主要结论

引理1[17]设f(x)∈Bn, 则

引理2[8]设f(x)∈Bn,若AI(f)=d,则

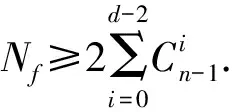
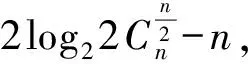
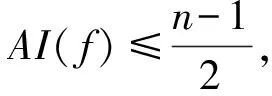
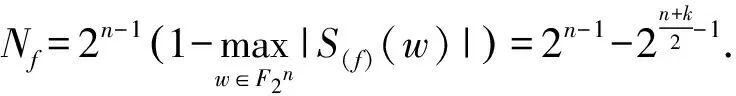
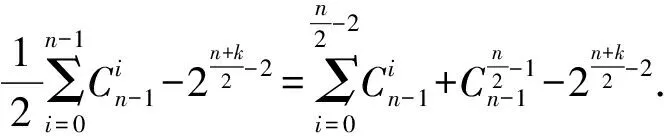
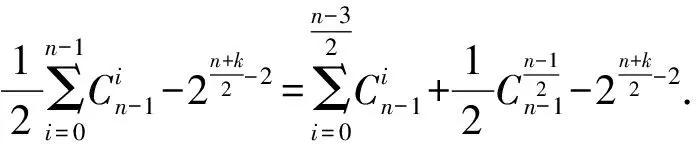
定理1给出了n元k阶拟Bent函数存在低次零化子的一个充分条件, 它只需要根据k与n的关系来进行判定, 而不需要利用Walsh循环谱或代数正规形来判定, 非常直观有效. 由定理1知, 在变元个数确定的情况下, 拟Bent函数的阶数越高, 其存在低次零化子的可能性越大, 抵抗代数攻击的能力越弱. 反之, 在阶数确定的情况下, 拟Bent函数的变元个数越大, 其存在低次零化子的可能性越小, 抵抗代数攻击的能力越强. 进一步, 还可分析拟Bent函数的阶数k与其变元个数n之间的距离对代数免疫性的影响.f(x)为此, 需要探讨一些组合数的性质.

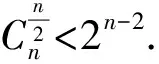
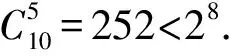
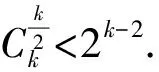
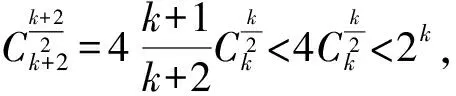
综合(1)、(2)知原命题成立.

类似可得如下结论:

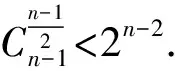
由定理1和结论1可得如下推论:

推论1 设f(x)是n元k阶拟Bent函数, 且n为偶数. 若n-k=2, 则对于一切n≥10,f(x)存在低次零化子.

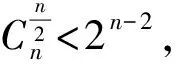
类似可得如下推论:

推论2 设f(x)是n元k阶拟Bent函数, 且n为奇数. (1) 若n-k=2, 则对于一切n≥5,f(x)存在低次零化子; (2) 若n-k=4, 则对于一切n≥11,f(x)存在低次零化子.

推论1和推论2表明, 拟Bent函数的阶数k与其变元个数n之间的距离对代数免疫性的影响很大, 距离越小, 代数免疫能力越弱.

进一步, 还可把定理1推广得定理2.

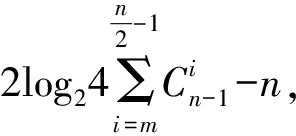
证明(1) 当n为偶数时, 由定理1的证明知,

(2) 当n为奇数时, 由定理1的证明知,

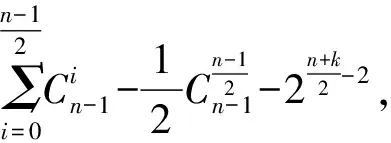
定理2表明, 可以根据拟Bent函数的阶数k与变元个数n之间的具体关系来确定其代数免疫度的上界.

3 结 语

本文研究表明当拟Bent函数的阶数k与变元个数n满足一定的关系时, 就可充分判定其存在低次零化子, 为密码系统中密码函数的选择提供了借鉴. 遗憾的是, 该条件是充分的而非必要的. 能否找到充要条件, 还有待进一步研究.

致 谢

感谢安徽省高校优秀青年人才计划给予的经费支持,诚挚感谢张福泰教授的辛勤指导!

[1] 李世取, 刘文芬, 滕吉红.k阶拟Bent 函数的性质及其应用[C]//谢仁宏. 第7 届全国青年通信学术会议论文集.北京: 电子工业出版社, 2001:939-943.

LI Shi-qu, LIU Wen-fen, TENG Ji-hong. Some properties ofk-order quasi-bent functions and its applications[C]//XIE Ren-hong. The proceedings of the Seventh National Youth Conference on communication. Beijing: Electronic Industry Press, 2001:939-943.(in Chinese)

[2] 滕吉红, 李世取, 刘文芬.k阶拟Bent 函数在密码设计和通信中的应用[J]. 通信学报, 2003, 24(12):58-66.

TENG Ji-hong, LI Shi-qu, LIU Wen-fen. The application ofk-order quasi-bent functions in cryptology and communication fields [J]. Journal of China Institute of Communication, 2003,24(12):58-66.(in Chinese)

[3] 张习勇, 韩文报. 拟Bent 函数的性质和构造[J]. 数学学报, 2004, 47(6):1175-1184.

ZHANG Xi-yong, HAN Wen-bao. Some properties and constructions of quasi-bent functions [J]. Acta Mathematica Sinica, 2004, 47(6):1175-1184.(in Chinese)

[4] 胡斌, 金晨辉, 冯春海. Plateaued 函数的密码学性质[J]. 电子与信息学报, 2008, 30(3): 660-664.

HU Bin, JIN Chen-hui, FENG Chun-hai. Cryptographic properties of plateaued functions[J]. Journal of Electronics & Information Technology, 2008, 30(3): 660-664.(in Chinese)

[5] 刘志高. 两类多输出一阶拟Bent函数的构造 [J]. 武汉工程大学学报,2010, 32(9):108-110.

LIU Zhi-gao. The constructions of two classes of 1-order multi-output quasi-bent functions[J]. Journal of Wuhan Institute of Technology, 2010, 32(9):108-110.(in Chinese)

[6] 王维琼, 肖国镇. Plateaued函数的对偶性[J]. 计算机科学, 2013, 40(5): 19-20.

WANG Wei-qiong, XIAO Guo-zhen. Dulity of plateaued functions[J]. Computer Science, 2013, 40(5): 19-20.(in Chinese)

[7] COURTOIS N, MEIER W. Algebraic attacks on stream ciphers with linear feedback [C]//Advances in Cryptology- EUROCRYPT 2003. Berlin:Springer-Verlag 2003: 346-359.

[8] MEIER W, PASALIC E, CARLET C. Algebraic attacks and decomposition of Boolean functions[C] //Advances in Cryptology-EUROCRYPT 2004. Berlin:Springer-Verlag 2004: 474-491.

[9] CARLET C, DALAI D K, GUPTA K C, et al. Algebraic immunity for cryptographically significant Boolean functions: analysis and construction[J]. IEEE Transactions on Information Theory, 2006, 52(7): 3105-3121.

[10] 张凤荣, 胡予濮. 具有高阶代数免疫的弹性函数[J]. 武汉大学学报:理学版, 2010, 56(2): 207-210.

ZHANG Feng-rong, HU Yu-pu. Resilient boolean functions with high algebraic immunity[J]. Journal of Wuhan University:Natural Science Edition, 2010, 56(2): 207-210.(in Chinese)

[11] 熊晓雯, 屈龙江, 李超. 具有最大代数免疫度的布尔函数的构造[J]. 计算机科学, 2011, 38(1): 26-30.

XIONG Xiao-wen, QU Long-jiang, LI Chao. Construction of boolean function with maximum algebraic immunity [J]. Computer Science, 2011, 38(1): 26-30.(in Chinese)

[12] 董新锋, 张文政, 周宇,等. 基于代数正规型构造的代数免疫最优布尔函数[J]. 计算机工程, 2013, 39(7): 169-172.

DONG Xin-feng, ZHANG Wen-zheng,ZHOU Yu,et al. Optimal algebraic immune boolean function based on algebraic normal form construction[J]. Computer Engineering, 2013, 39(7): 169-172.(in Chinese)

[13] 冯克勤, 廖群英. 对称布尔函数的代数免疫性[J]. 工程数学学报, 2008, 25(2): 191-198.

FENG Ke-qin, LIAO Qun-ying. On algebraic immunity of symmetric boolean functions[J]. Chinese Journal of Engineering Mathematics, 2008, 25(2): 191-198.(in Chinese)

[14] 吴玮玲, 王永娟, 张世武. 奇数变元plateaued函数代数免疫性质研究[J]. 计算机工程与应用, 2012, 48(2): 96-98.

WU Wei-lin, WANG Yong-juan，ZHANG Shi-wu. On algebraic immunity of plateaued functions in odd variables[J]. Computer Engineering and Applications，2012, 48(2): 96-98.(in Chinese)

[15] 刘志高. 级联函数的代数免疫性研究[J]. 计算机工程, 2012, 38(1): 117-119.

LIU Zhi-gao. Research on algebraic immunity of Boolean functions by concatenation[J]. Computer Engineering, 2012, 38(1): 117-119.(in Chinese)

[16] 周宇, 曹云飞, 张文政，等. 布尔函数的代数免疫与扩散阶的关系[J]. 计算机工程与科学, 2011, 33(10): 34-38.

ZHOU Yu, CAO Yun-fei,ZHANG Wen-zheng et al. Relationship between algebraic immunity and propagation characteristics of the boolean functions[J]. Computer Engineering & Science, 2011, 33(10): 34-38.(in Chinese)

[17] 冯登国. 频谱理论及其在密码学中的应用[M]. 北京: 科学出版社, 2000:41-45.

FENG Deng-guo. Spectrum theory and its applications in cryptography[M]. Beijing: Science Press, 2000:41-45.(in Chinese)