棱角反射波幅度法测量裂纹高度的研究
2014-02-27韩晓华孟令华
韩晓华,刘 畅,于 冰,董 欣,孟令华
(1.山东省科学院激光研究所,山东 济宁 272017;2.中国科学院金属研究所,辽宁 沈阳 110016)
棱角反射波幅度法测量裂纹高度的研究
韩晓华1,刘 畅2,于 冰2,董 欣1,孟令华1
(1.山东省科学院激光研究所,山东 济宁 272017;2.中国科学院金属研究所,辽宁 沈阳 110016)
提出一种对裂纹高度超声棱角反射测试的改进方法,推导裂纹高度Hf(或面积Af)与裂纹棱角反射回波幅度Pf和无限大棱角反射回波幅度PB的方程。应用提出的计算公式,并辅以简便快捷的Matlab计算,可避免加工和使用试块,从而能够简便快捷地测量裂纹的高度,测量过程简单方便,无盲区。
裂纹高度;超声横波;棱角反射法
0 引 言
表面裂纹是一种常见的缺陷,发现表面裂纹的探伤方法较多,例如磁粉、渗透、涡流、目视、超声表面波、超声横波棱角反射等。发现裂纹之后,在许多情况下还需要裂纹高度的数据,特别是进行安全评定时,裂纹的高度是不可缺少的。但是能测量表面裂纹高度的方法比较少,常用的方法有超声表面波、超声TOFD、超声棱角反射和透射波半高度法[1-5]。它们有各自的优点和局限性。
本文对棱角反射法加以改进,只需要测量裂纹棱角反射波与可视为无限大的棱角反射波的幅度比,再经过简单的计算,便能得出裂纹高度,无需制作试块以及测量并绘制标定曲线。
1 用棱角反射测定裂纹高度的计算公式
斜探头的声场在许多超声探伤教材中都有论述,都是采用虚拟等效源模型[6],如图1所示。S是探头晶片,S1是虚拟等效探头的晶片。假定探头晶片S长度是2L,高度是2H,虚拟探头S1的晶片长度是2l,高度是2l,则:

这里α是探头的入射角,β是折射角。假定探头的楔内声程是rpro,折合到被检工件内的等效声程是req。

下面讨论棱角反射回波的幅度Pf。假定裂纹与工件表面垂直,如图2所示,入射声束被裂纹M1O与工件下表面N1O反射,由此产生棱角反射波E1。设想在裂纹顶端有一个孤立的并且与声束垂直的反射面MN,入射声束被平面MN反射,由此产生回波E2。不难证明E1和E2相同。
声源S1在反射面MN产生的入射波的声压Pin。

式中:Tin——超声波从有机玻璃进入钢时的透射率;
P0AS1——晶片发射面上的总的振动力F=P0AS1。
探头声束的截面尺寸有限,而且截面上声压分布不均匀,声压分布的规律很早就被发现了,并且得到了描述声压分布的数学公式[7]。如图3所示,XY平面上的小矩形代表发射晶片,它向Z轴方向发射超声波。声轴上的声压P(r,0,0)和声轴之外某点M的声压P(r,a,b)可表示为
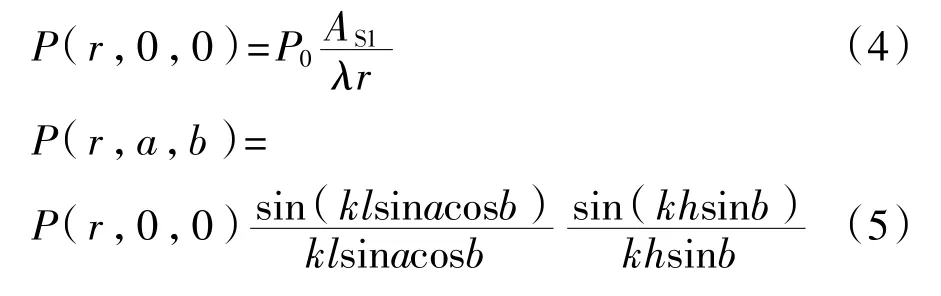
式中:2l——晶片长度;
2h——晶片高度;
r——M点所在截面到直角坐标原点(0,0,0)的距离;
b——MO与XZ平面之间的夹角;
a——MO在XZ平面上的投影与Z轴之间的夹角。
本文进行实验的条件是钢试块,K1斜探头,晶片尺寸13mm×13mm,频率2.5MHz。由此得出的波长λ=1.3mm,虚拟声源S1的长度是2l=13mm,S1的高度由式(6)得出:

β=45°,α=36.54°,2h=11.44mm。根据扩散角的公式,可求出声扩散角:

求出的声束在X方向扩散角φL=5.7°,Y方向扩散角φH=6.5°。测得的探头有机玻璃楔内声程xpro=9.77 mm≈10 mm,用式(2)计算得出等效声程req=7.41 mm,实验用的低碳钢试块的截面是40 mm× 40mm正方形,由式(8)得出:
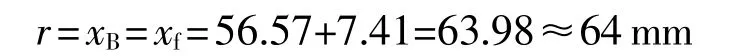
在扩散角外面声能很少,可以只对扩散角之内的区域进行分析,这样角b的最大值bmax=6.5°,角a的最大值amax=5.7°,因此可以近似地用cosb=1将式(5)简化。式(5)中的函数是一个工程上常用的函数,叫做采样函数或Sa函数也是一个常用的函数,叫做正弦积分函数或Si函数且Si(x)的数值有函数表可查[8-9]。
如果在r处有一个与r垂直的反射面,它的长和高分别是2U和2V,反射面受到的总的作用力可以用式(5)来计算。由于角a<<1和角b<<1,式(5)可简化为
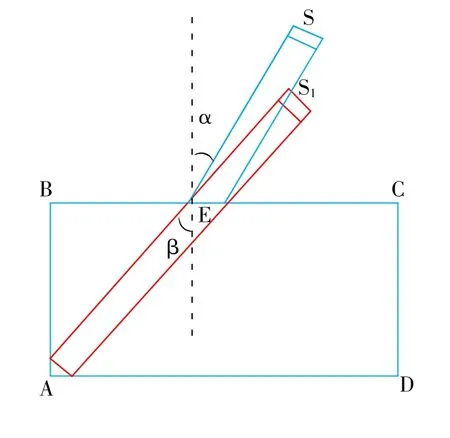
图1 斜探头声场的发射源和虚拟等效源
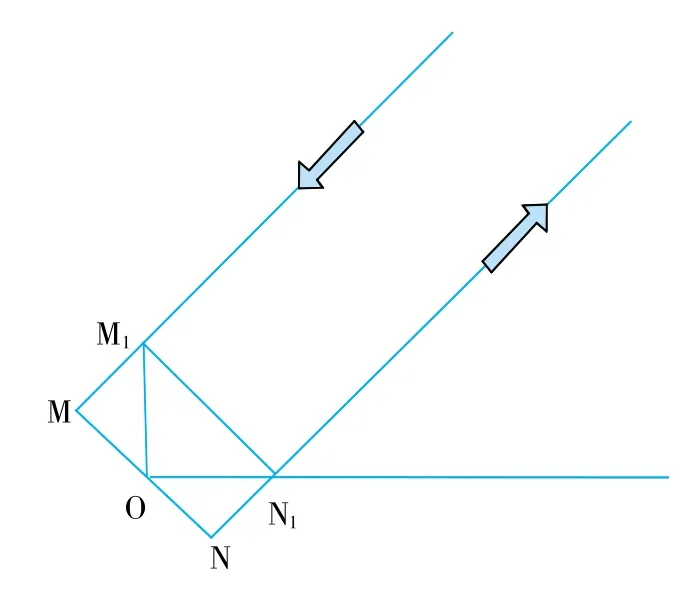
图2 表面裂纹(M1O)棱角反射示意图
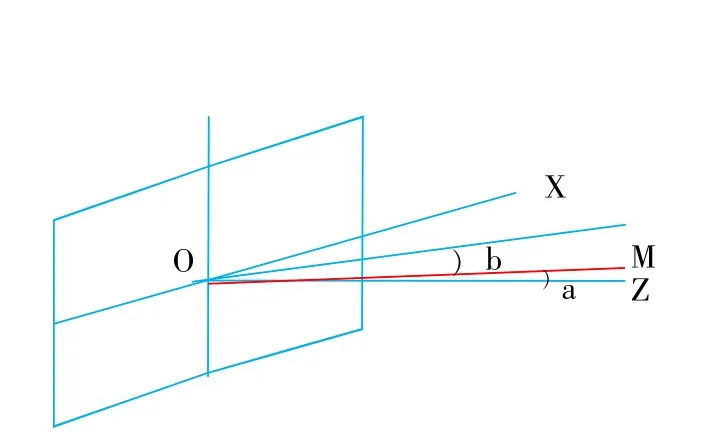
图3 方形发射晶片的声场中某点M的声压

反射面MN受到的总作用力F为
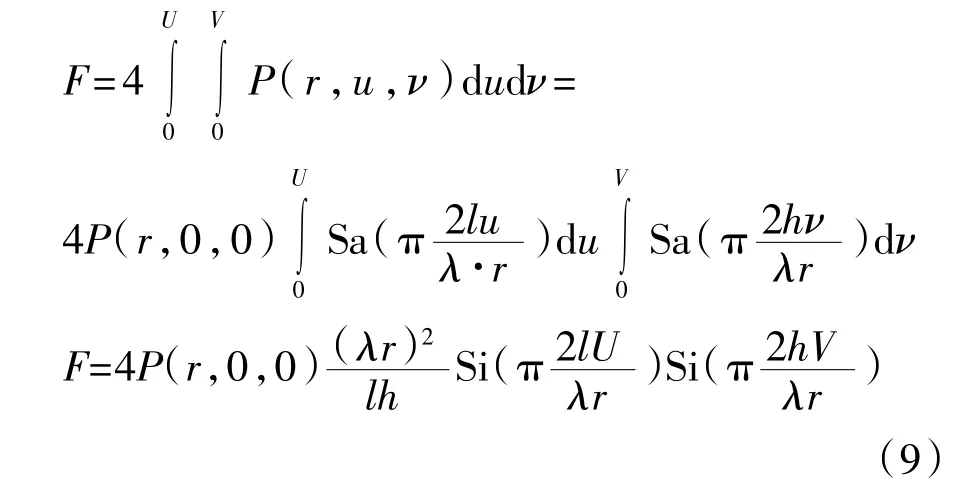
根据式(9)得出探头接收到的反射回波声压为
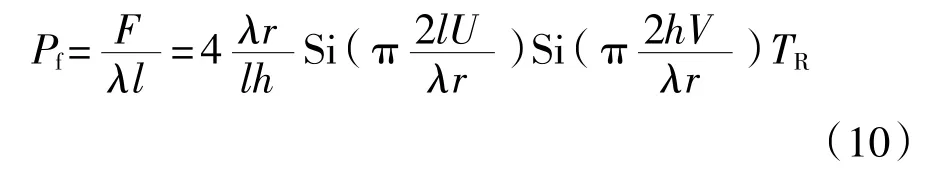
式中:TR——有机玻璃与钢之间的往复透射率,与探头折射角β有关。
下面讨论无限大棱角的棱角反射回波。探头发射声场的范围基本上是在扩散角以内,所以当反射面的面积达到扩散角的边界之后,反射面继续增大,回波幅度升高很小,可以忽略不计[10]。因此,可将扩散角边界作为反射面的饱和值。尺寸等于或超过饱和值的棱角,可视为无限大棱角。按扩散角的定义,式(8)中的两个Sa函数的第一个零点就是X和Y两个方向上的扩散角。当x=π时,Sa(x)=0。因此反射面X和Y两个方向上的饱和尺寸US和VS分别是
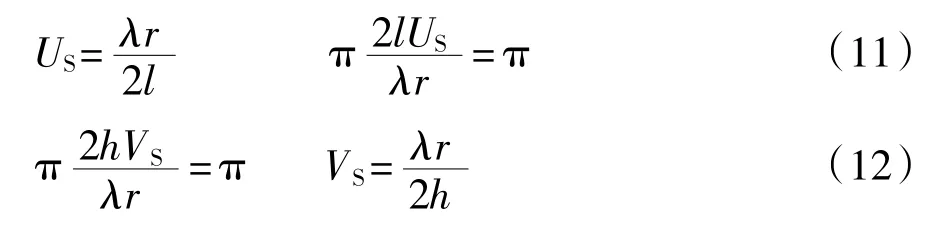
本文的实验条件是虚拟晶片长2l=13 mm,高2h=11.44mm,λ=1.3mm,声程r=64mm,β=45°。由此得出虚拟等效反射面临界长度2U0=12.8mm,临界高度2V0=14.6 mm,由此得出裂纹长度饱和值Lfs和裂纹高度饱和值Hfs。
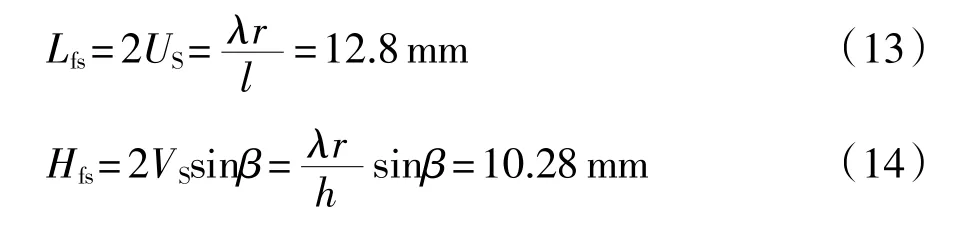
在裂纹尺寸达到临界(或饱和)时,即式(8)中两个Sa函数都达到第一个零点,此时它的自变量等于π,此时式(9)和式(10)中Si函数的自变量当然也等于π,计算得出Si(π)=1.8529。由此得到无限大棱角反射回波幅度为

2 测定裂纹高度的方法和实验结果
如图2所示,假想的反射面MN的高度2 V与裂纹的高度Hf之间有如下关系:

为了便于计算将式(20)代入式(17),再将选用的超声测量参数共4个代入式(17),这些参数是:λ=1.3 mm,h=5.72 mm,r=64 mm,sinβ=sin45°=0.707。由此得到:
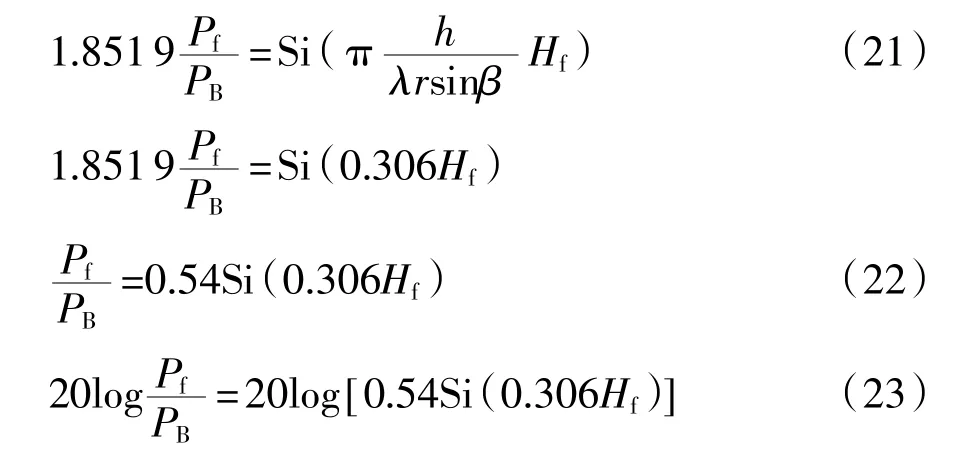
按式(23)编写了简单的Matlab计算程序,将设定的裂纹高度Hf写入程序,运行该程序计算出裂纹棱角反射波与无限大棱角反射波幅度比的分贝数。为了考核提出的裂纹高度测试方法是否可行,得出公式是否精确,设计了3个试块,试块材
料是20号钢。1号试块上带有4个线切割槽,它们的深度分别是:0.2,0.4,0.6,0.8 mm。2号试块也有4个线切割槽,它们的深度分别是1,3,5,7mm。3号试块上有3个线切割槽,它们的深度分别是:10,20,30 mm。试块形状为长条形,截面是40mm×40mm的正方形,长度200mm。线切割槽横穿试块,槽的间距是40mm。
对深度10mm以下的9个槽进行了棱角反射回波幅度Pf测量,同时也测量了试块端头的棱角反射回波幅度PB。使用的仪器是CTS2000型,探头是普通的K1斜探头,2.5 MHz,晶片13 mm×13 mm,测得的楔内声程10mm。用测得的计算出线切割槽的深度Hf。槽深Hf的超声测量值和真实值列于表1。
3 结果与讨论
式(23)表达了表面裂纹棱角反射波Pf与大棱角反射波PB的幅度比的分贝数与裂纹高度Hf的数量关系,但是,由于公式包含着特殊函数Si(x),不能直接计算。为此编写了两个Matlab计算程序,第1个用于已知裂纹高度Hf,计算分贝数之差第2个用于逆计算,即已知分贝数之差计算裂纹高度Hf。

表1 线切割槽深度测量值与真实值的对比
虽然本文的实验是测量无限长的线切割槽的深度,实际上只有槽的中心附近、扩散角以内的部分对入射波有反射作用,其余部分作用很小,可以忽略。如前所述扩散角以内的槽的长度是10.7mm,因此槽深就是槽的有效反射面积,将试块上的槽深0.2~10mm换算成面积当量,结果为3.03~ 151mm2;换算成平底孔当量,结果为φ1.96~φ13.88mm。有了面积当量,已知裂纹长度,就能计算裂纹高度。
对此表1最下面两行同一列的数值,可以看到,刻槽棱角反射波与大棱角反射波幅度比的分贝数计算值与测量值之差在接触法手工测量回波幅度的误差范围之内,约±3dB。±3dB将产生±41.3%的裂纹高度测量误差,这表明误差主要来自回波幅度测量。采用水浸法或喷水探头代替接触法,有可能减小回波幅度测量误差[11]。
4 结束语
棱角反射波幅度法测量裂纹的高度行之有效,计算值与测量值之差在接触法手工测量回波幅度的误差范围之内,测量方法的主要优点是无盲区和能够测量高度很小的裂纹,例如0.1mm的裂纹。应用本文提出的计算公式,避免了加工和使用试块,代之以简便快捷的Matlab计算,测量过程简单。
[1]郑中兴.材料无损检测与安全评估[M].北京:中国标准出版社,2004:191-197.
[2]张薇,蔡桂喜.TA38型空压机转子表面裂纹检验及深度测量[J].无损探伤,2009,33(3):36-38.
[3]强天鹏,肖雄,李志军,等.TOFD技术的检测盲区计算和分析[J].无损检测,2008,30(10):738-740.
[4]彭伟,尤卫宏,张俊杰,等.焊缝探伤超声TOFD法与射线照相法检验对比研究[J].无损探伤,2001,35(4):40-41.
[5]韩晓华,张薇,杨阳,等.透射波半高度法测量裂纹高度的研究[J].中国测试,2012,38(6):9-12.
[6]郑晖,林树清.超声检测[M].北京:中国劳动社会保障出版社,2008:62-63.
[7]安德烈·安戈.电工电信工程师数学下册[M].谢祥麟,陆志刚,曾德汲,译.北京:人民邮电出版社,1979:10-15.
[8]姚力.焊缝缺陷超声波定量检测方法探讨 [J].无损检测,1998,30(2):11.
[9]Chohen R L,West K W.Crack measurement in metals by the four point probe technique[J].Materials Evaluation,1990,48(1):30-34.
[10]孙继华,赵洪贤.基于有限元方法的凹槽超声检测[J].计测技术,2009,29(6):28-31.
[11]成海涛.无逢钢管缺限与预防[M].成都:四川科学技术出版社,2007:85-86.
Study on measurements of crack heights with amplitude of echo from right angle edge
HAN Xiao-hua1,LIU Chang2,YU Bing2,DONG Xin1,MENG Ling-hua1
(1.Institute of Laser Research,Shandong Academy of Sciences,Jining 272017,China;2.Institute of Metal Research,Chinese Academy of Sciences,Shenyang 110016,China)
This paper proposes an improved method for measuring crack height with ultrasonic wave echo from corner refection of crack,and derives an equation of the crack height which governs the ratio of the crack corner echo amplitude Pf of ultrasonic wave to the infinite plane echo amplitude PB ofultrasonic wave.With the proposed equation and MATLAB aided calculation,processing test blocks and using them can be avoided.Experimental results show cornerreflection method to measure the crack heightis simple and convenient, and the measurement is no blind spots.
crack height measurement;ultrasonic shear wave;corner reflection method
TG115.285;TH878+.2;TG111.91;O346.1+2
:A
:1674-5124(2014)01-0017-04
10.11857/j.issn.1674-5124.2014.01.005
2013-04-17;
:2013-06-28
山东省自主创新成果转化重大专项(2007zhzx10130)
韩晓华(1957-),男,江苏徐州市人,研究员,主要从事无损检测技术的研究和管理。
