小样本条件下双应力步降加速退化试验优化设计

吕 萌,蔡金燕,梁玉英,潘 刚,张国龙,孟 军

（军械工程学院，河北 石家庄 050003）

小样本条件下双应力步降加速退化试验优化设计

吕 萌,蔡金燕,梁玉英,潘 刚,张国龙,孟 军

（军械工程学院，河北 石家庄 050003）

针对小样本条件下高可靠性长寿命产品的性能往往受到多个应力的影响，且在加速退化试验中该类产品在有限试验时间内难以获得大量性能退化信息的问题，提出一种小样本条件下双应力步降加速退化试验优化设计方法。采用Monte-Carlo对加速试验进行仿真模拟，在样本量大小一定的条件下，以监测频率、应力水平数、监测次数作为设计变量，以总的试验费用作为约束条件，以正常使用应力下的p阶分位寿命渐进方差估计作为目标函数，建立小样本条件下双应力步降加速退化试验优化设计模型。通过仿真实例，验证该方法的有效性、可行性。

小样本；性能退化；双应力步降加速退化试验；优化设计

0 引言

加速退化试验是解决高可靠性、长寿命产品可靠性评估的一个重要技术途径，Shuo-Jye Wu等[1]对在费用约束条件下的退化试验优化设计进行研究；LC Tang等[2]以试验费用最少为目标，对随机过程分布下的步进加速退化试验设计方法进行了研究；Zheng-zheng Ge等[3]在试验截尾时间和样本量大小的约束下，以正常使用应力下的p阶分位寿命可靠度渐进方差估计为目标，对布朗运动模型下步进加速退化试验优化设计进行研究；Jing-Rui Zhang等[4]以试验费用作为约束，以正常使用应力下产品可靠度均方误差为目标，对布朗运动模型下的步降加速退化试验优化设计进行研究；Hong-F Yu[5]对倒数weibull分布退化率下的加速退化试验优化设计进行了研究；Xiao-yang Li等[6]对竞争失效模型下的步降加速退化试验优化设计进行了研究，潘正强等[7]对基

于Wiener过程的多应力加速退化试验设计进行了研究。然而小样本条件下以费用作为约束的双应力步降加速退化试验的优化设计研究相对较少，对小样本量条件下电子产品的试验优化问题没有较为完善的理论支持。因而本文将采用Monte-Carlo仿真的方法对双应力步降加速退化试验进行模拟，在小样本条件下以费用作为约束，对混合效应模型下的双应力步降加速退化试验进行分析。

1 小样本条件下双应力步降加速退化试验方法

文献[8]对双应力步进加速退化试验统计分析方法进行了研究。设有两组应力水平S1和S2，每组应力组合包含一系列应力水平，为后续方便分析，在此假定两组应力水平数及应力组合数大小均为k。

在满足上述假设的前提下对试验过程具体描述如下：

在试验样本大小n一定的条件下，首先给出k个监测周期T1，T2，T3，…，Tk；其次将选取的样本置于最高应力水平组合下监测T1小时；然后放入下组应力水平组合下监测T2小时；如此试验下去，直到最后一组应力水平组合其中Ti是应力组合水平持续的时间。

2 模型假设

2.1 退化模型假设

假设在第i个应力组合下样本的退化轨迹可用以下混合效应模型描述：

其中i=1，2，…，k；j=1，2，…，k；l=1，2，…，n；hi=1，2，…，mi。

式中：Φ——退化量；

βil＞0——第i个应力水平组合下第l个样品的随机特征，βihi-1～Weibull（m，ηi），m为形状参数，ηi为分布参数；

tihi——i个应力组合水平下的监测时间点；

α＞0——固定常数。

εikhi（ti，k）——测量误差，相互独立且服从标准正态分布

2.2 物理模型假设

退化轨迹参数中的随机效应参数βil服从GΘ（·）分布，分布参数中ηi与应力存在如下关系：

3 优化问题描述

3.1 设计变量

（1）应力水平组合数k；（2）加速应力水平组合下的监测频率；（4）gij为监测次数，且gij≥2，因而试验的总时间其中tu为单位时间（小时）。从而试验方案可表示为

3.2 优化目标

选用正常使用应力水平下p阶分位寿命渐近方差的局部估计值作为目标函数，即

3.3 约束条件

在样本量一定的条件下，因费用主要由监测方面的费用组成，故可以用费用函数来代替时间函数对试验中的设计变量进行约束，具体如下：

式中：gij≥2，fij＞0，且n和gij均为正整数；

Cm——监测单个样本监测一次所需的费用；

Cs——单个样本费用；

Ce——单位时间的操作费用[1]。

4 优化设计方法

4.1 优化算法

图1为小样本条件下双应力步降加速退化试验优化设计流程图。

第1步 在样本量n给定的条件下，由式（4）可计算得试验应力水平组合数ku=[（Cb-nCs）/（Ce+2nCm）]，监测频率fu=[（Cb-nCs-2knCm）/（kCe）]的上限，[·]为取整函数；利用式（4）寻找所有的gi，构造应力水平并计算各应力水平大小其中i=1，2，…，k；j=1，2，…，k。通过对上述变量计算完成对试验方案集的构造。

图1 小样本条件下双应力步降退化试验优化设计流程图

第2步 在备选方案集D中选取一个试验方案其中R为备选方案的个数。

第3步 利用Monte-Carlo方法，模拟双应力步降加速退化试验Q次，得到Q组模拟试验数据：

第4步 通过对ycilhi进行统计分析，计算目标函数值fq，r（d）。

将其作为目标函数值fr。

第6步 返回第2步选取另一个试验方案重复第2～5步，直至第R个方案完成，目标函数集为f= {fr，r=1，2，…，R}；

第7步 选取使得目标函数值fr达到最小的方案作为最优试验方案d*。

4.2 目标函数的计算

目标函数的计算主要涉及p阶分位寿命ξp的推导、数学模型及物理模型中先验参数的估计及AVar（ξp）的计算。其中模型中相关参数的估计比较简单，可以参照文献[1]给出的最小二乘估计方法进行求解，这里重点给出AVar（ξp）的计算方法。

首先给出对数似然函数如下：

然后通过对式（6）求二阶偏导可得到局部Fisher矩阵：

其中，l为对数似然函数，矩阵各项为l的二阶偏导数在的值。

根据文献[5]可很容易推导出p阶分位寿命的极大似然估计为

则p阶分位寿命ξp0的渐近方差估计为

其中

5 实例分析

采用文献[5]中的实例进行分析，发光二极管（LED）的使用寿命受到温度和电流影响，其中该型LED的正常使用温度为278K，最低加速应力温度为298 K，最高为378 K；正常使用电流25 mA，最低加速电流为28 mA，最高为40 mA。费用参数分别为：Cb=2 000元/h，Cs=55元/h，Cm=0.3元/h，Ce=0.6元/h。试验样品的先验信息如下：

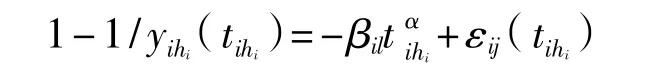
为简化优化问题，特对试验变量做以下假设：

（1）为了简化计算方便分析在此将应力设置为等间隔，即

（2）在温度最高为378K，最低为298K，电流最高为40mA，最低为28mA的应力水平组合下，样本大小n=5和n=8时，按照本文提出的方法对双应力步降加速退化试验优化设计进行分析。具体情况如表1、表2所示。

比较分析表1与表2，可以得到如下结论：

（1）在试验费用（试验截尾时间）及样本量大小一定的条件下，目标函数的值随着应力水平数的增加呈现先减小的趋势。

（2）样本量大小及应力水平数一定的条件下，目标函数的值随着试验费用（试验截尾时间）的增加呈现减小的趋势。

在实际试验时，还需考虑应力水平大小对优化试验方案的影响，表3给出了n=8，k=3时最高应力水平变化时的优化试验方案。

表1 小样本条件下双应力步降加速退化试验优化设计结果（n=5)

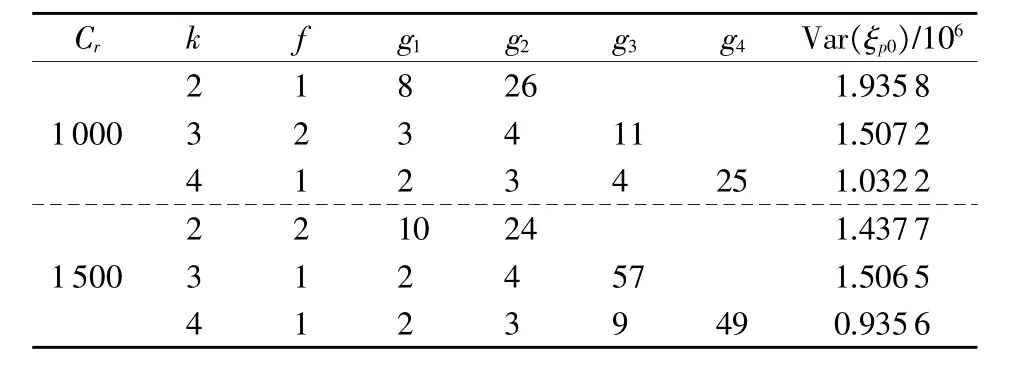
表2 小样本条件下双应力步降加速退化试验优化设计结果（n=8)

从表3中可以得出，当最低应力水平Tmin、Vmin一定时，目标函数值AVar（ξp0）随着最高应力水平Tmax、Vmax的减小呈现先减小后增大得趋势。

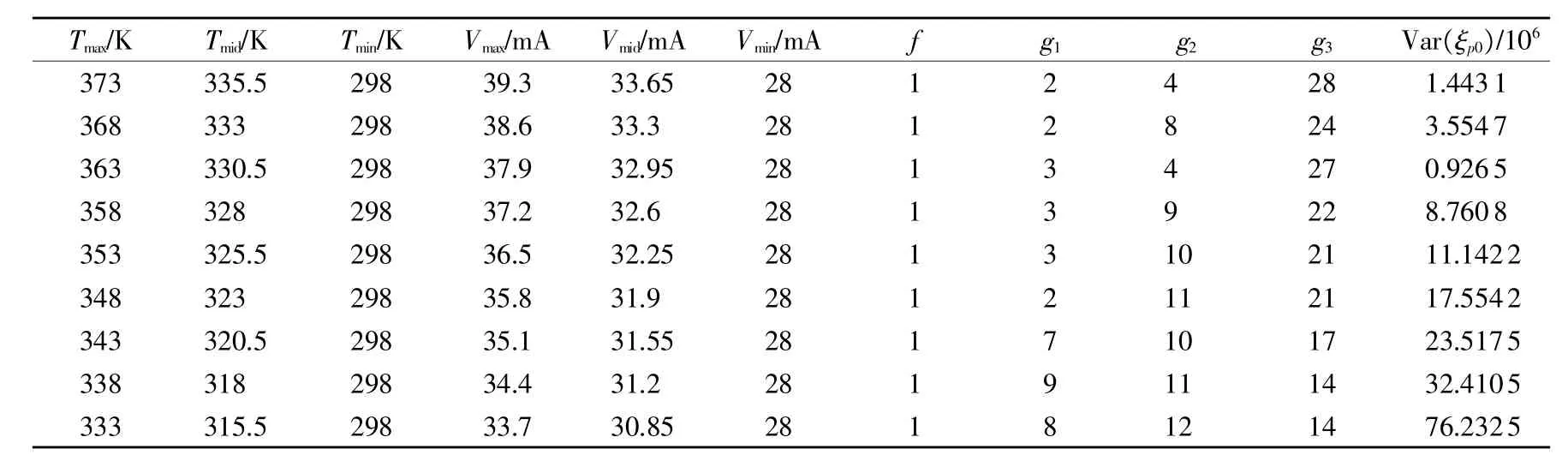
表3 小样本条件下双应力步降加速退化试验优化设计结果（n=8)

6 结束语

本文对小样本条件下双应力步降加速退化试验优化设计进行了讨论，给出在小样本量条件下双应力步降加速退化优化设计的一般方法，分析不同小样本量条件下，在不同费用约束下的最优试验方案；同时以n=8，k=3为例分析一定费用条件下应力变化对最优试验方案的影响，得出一些指导小样本下双应力步降加速退化试验的有用结论，补充和完善了加速退化试验优化设计理论框架。

[1]Wu S J，Chang C T.Optimal design of degradation tests in presence ofcostconstraint[J].Reliablity Engineering and System Safety，2002，76（2）：109-115.

[2]Tang L C，Yang G Y，Xie M.Planning of step-stress accelerated degradation test[C]∥ RAMS，Los Angeles，USA，2004：278-292.

[3]Ge Z Z，Li X Y，Zhang J R.Planning of step-stress accelerated degradation test with stress optimization[C]∥Advanced Materials Research，Germany，2010：118-120，404-408.

[4]Zhang J R，Jiang T M，Li X Y，et al.Optimization of step stress accelerated degradation test plans[C]∥17th Interna tional Conference on Industrial Engineering and Engineering Management，IE and EM 2010，China，2010（10）：947-951.

[5]Yu H F.Designing an accelerated degradation experiment with a reciprocal weibull degradation rate[J].Journal of Statistical Planning and Inference，2006，136（1）：282-297.

[6]Li X Y，Jiang T M.Optimal design for step-stress accel erated degradation with competing failure modes[C]∥Annual Reliability and Maintainability Symposium，2009：64-68.

[7]潘正强、周经伦，彭宝华.基于Wiener过程的多应力加速退化试验设计[J].系统工程理论与实践，2009，8（29）：64-71.

[8]汪亚顺，莫永强，张春华，等.双应力步进加速退化试验统计分析研究——模型与方法[J].兵工学报，2009，30（4）：451-456.

Optimization design of double-step-down-stress accelerated degradation test for small sample

LÜ Meng，CAI Jin-yan，LIANG Yu-ying，PAN Gang，ZHANG Guo-long，MENG Jun
（Ordnance Engineering College，Shijiazhuang 050003，China）

Performance of the high reliability and long life products on the condition of the small sample are affected by several stresses and it is hard to get the performance degraded information in limited test time in accelerated degradation test.This paper presented a method of optimal designs for the double-step-down-stress accelerating degradation test on condition of small sample.Simulating procedure of the test with Monte-Carlo and on the condition of the sample size was specified.Numbers of stress and inspection frequency were considered as variables. Asymptotic variance estimation of 100pth percentile of the lifetime distribution of the product at use condition was considered as goal function under the constraint of the total experiments cost. Finally，optimal designed model of the double-step-down-stress accelerated degradation test on condition of the small sample was established.Simulation results verify feasibility and the validity of this method.

smallsample； performance degradation； double-step-down-stressaccelerated degradation test；optimal design

TH123+.4；TJ206；TB114.3；TP277.3

：A

：1674-5124（2014)03-0129-04

10.11857/j.issn.1674-5124.2014.03.034

2012-08-05；

：2012-10-11

河北省重点基金项目（109635529D）

吕 萌（1984-），男，河北石家庄市人，博士研究生，研究方向为武器性能检测与故障诊断。