非线性动态WPLS航煤干点软测量

邹涵

（南京工业大学电子与信息工程学院，江苏 南京 211816）

非线性动态WPLS航煤干点软测量

邹涵

（南京工业大学电子与信息工程学院，江苏 南京 211816）

针对炼油工业过程存在的多变量、非线性和数据动态性问题，提出一种自回归移动平均模型与径向基函数-加权偏最小二乘相结合的非线性动态建模方法。首先建立基于径向基函数-加权偏最小二乘方法的软测量模型，然后利用自回归移动平均模型对数据进行时序分析校正，将动态误差信息加入到模型中去，实现模型的动态装换。将该方法应用到加氢裂化航煤干点的软测量建模中，从而获得比径向基函数-加权偏最小二乘算法更高的预测精度。

径向基函数；自回归移动平均模型；偏最小二乘；干点；软测量

0 引 言

在炼油工业的生产过程中，干点是衡量分馏产品质量的一个关键指标，直接影响到其质量和收率的高低。但是，该指标是规格参数，无合适的在线分析仪进行测量，只能离线分析且时间长。因此，建立性能优良的干点软测量模型，可以实现干点质量指标的预测，并为生产操作提供指导。目前，软测量已提出很多方法，有多种全局多元线性回归方法[1-3]，具有简洁明确的表达形式，但难以描述非线性系统。为了处理非线性问题，又提出了多种非线性软测量方法[3-4]，然而由于过程生产中自身控制要求的改变、本身特性的变化以及现场环境对其影响，使得过程生产通常处于动态，利用静态建模方法难以体现动态特性，造成模型预测精度低且不能持续使用。所以仅仅考虑非线性特性是不够的，需要将对象的动态信息融合到模型中去。

本文提出一种自回归移动平均（autoregressionmnving average，ARMA）模型与径向基函数-加权偏最小二乘（Radial basis function-Weighted partial least regression,RBF-WPLS）相结合的软测量方法。该方法首先建立基于RBF-WPLS的软测量模型，即将具有非线性样本数据映射到高维特征空间中，在高维特征空间中建立WPLS线性回归模型；然后，利用ARMA模型对数据进行动态估计，通过增加动态校正环节，实现了对静态模型的动态校正。

1 径向基函数-加权偏最小二乘回归

1.1 加权偏最小二乘回归

加权偏最小二乘回归方法是对偏最小二乘回归方法的改进算法。下面对PLS原理[5]做简单描述：

设样本容量为n，自变量数据矩阵X为n×p（n＞p）维，因变量数据矩阵Y为n×q（n＞q）维，提取PLS主元采用NIPALS算法[6]。设T是前t个PLS成分组成的n×t维隐变量矩阵，且有T=XU，则PLSR模型

式中：U——p×t维转换矩阵；

C——t×q维回归系数矩阵；

E——n×q维的残差矩阵。

在NIPALS算法中可同时计算出C与U，则q个因变量的预测值可以如下回归方程计算：

现实情况中，由于每个样本贡献率不同，导致其权重也不同。为了体现这种情况，可以采用加权回归方法[7]，即对各个样本赋予不同的权值，权值回归模型为

式中：W——权值系数。

权值大小需根据样本和预测对象之间的欧氏距离来分配大小。欧式距离与预测能力呈负相关关系[7]。即样本与预测对象的欧式距离越大，所分配的权值将越小。确认权值系数有很多种方法，本文采用一种较简单的方法。设权值分配参数为m（m为正整数），则与预测对象欧式距离最近的前m个样本权值为1，其余样本权值为0。

1.2 径向基函数-加权偏最小二乘回归

径向基函数-加权偏最小二乘回归算法是在加权偏最小二乘算法之前进行径向基函数的非线性变换。通过输入空间映射到一个新的空间，输出层在新的空间中进行线性组合，从而将线性不可分问题转化为线性可分[8]。本文采用最常用的高斯径向基函数做为隐含层节点的径向基函数。其隐含层节点的加权输出为

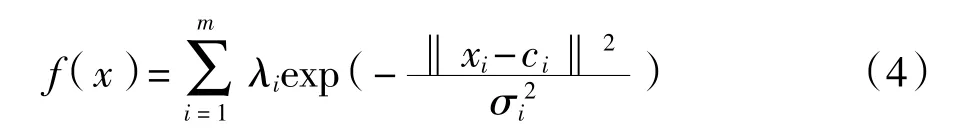
式中：λi——隐含层输出的权值系数；

m——径基个数；

ci，σi——第i个是高斯函数的中心和宽度参数；

‖·‖——欧式范数。

RBF网络中需要学习3个参数，即高斯函数的中心ci、宽度σi以及隐含层输出的权值系数λi。高斯函数的中心ci和宽度σi可以采用K-均值聚类方法[9]确定，权值系数λi可以采用偏最小二乘方法算出。

2 ARMA模型

ARMA模型[10]是研究时间序列、用于平稳时间的重要方法。即序列的当前值除了与自身的过去值存在关系，并且还与其以前进入系统的外部干扰存在一定的依赖关系，则该模型在表现刻动态特性时，模型中既包括自身的滞后项，也包括过去的外部干扰误差项。通常ARMA模型可表示为

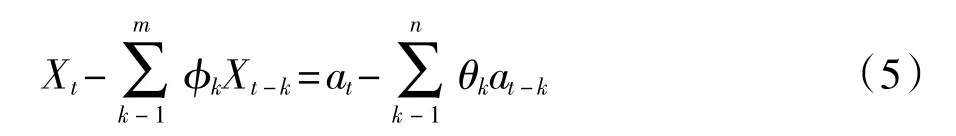
对其引入后向算子B有：Bxt=xt-1，B2Xt=Xt-2，（c为常数）。对于上述ARMA模型表达式，分别令：

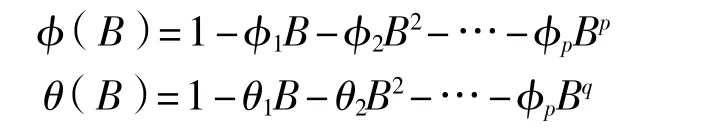
则式（5）转变为如下表达式：

式中：xt——正态、平稳的时间序列；

at——随机干扰误差项；

B——延迟算子；

φ（B），θ（B）——算子多项式。

模型称为p阶自回归、q阶滑动平均模型，记作ARMA（p，q）。

ARMA（n，n-1）模型具有将随机平稳系统逼近到任意精度的功能，通过递增法逐步逼近，需找适合的n值，确定模型阶数n。同时，n以2为递增量，不需要对ARMA（n，n-1）（（q≠p-1））模型的讨论，从而降低复杂度[11]。

对于ARMA（n，n-1）模型阶次的确定，利用F校验方法来判定。从n取1开始逐渐增大取值，直到获得满意的模型阶次。设H0：φ2n+2=0，θ2n+1=0，Q0为ARMA（2n+2，2n+1）模型残差平方和，Q1为ARMA（2n，2n-1）模型残差平方和，则：

式中：s——被校验参数的个数；

r——模型参数的总个数；

n——样本长度。

若F＞Fa，则H0不成立，模型将继续增加阶次；否则，ARMA（2n，2n-1）是合适的模型。而Fa的值可由F分布表和预先给定的置信度a来确定。

3 ARMA-RBF-WPLS算法

首先利用RBF-WPLS算法建立软测量预测模型，将该模型训练输出值yˆm与真实测量ym值相减，

得到一个关于输出值误差Δym的时间序列值，利用ARMA（n，n-1）模型对该时间序列进行建模，得到关于预测误差的ARMA模型。将以上两个模型相结合进行模型预测时，RBF-WPLS模型输出值减去ARMA模型的误差值，即得到输出变量的预测结果。该模型结构框图见图1。

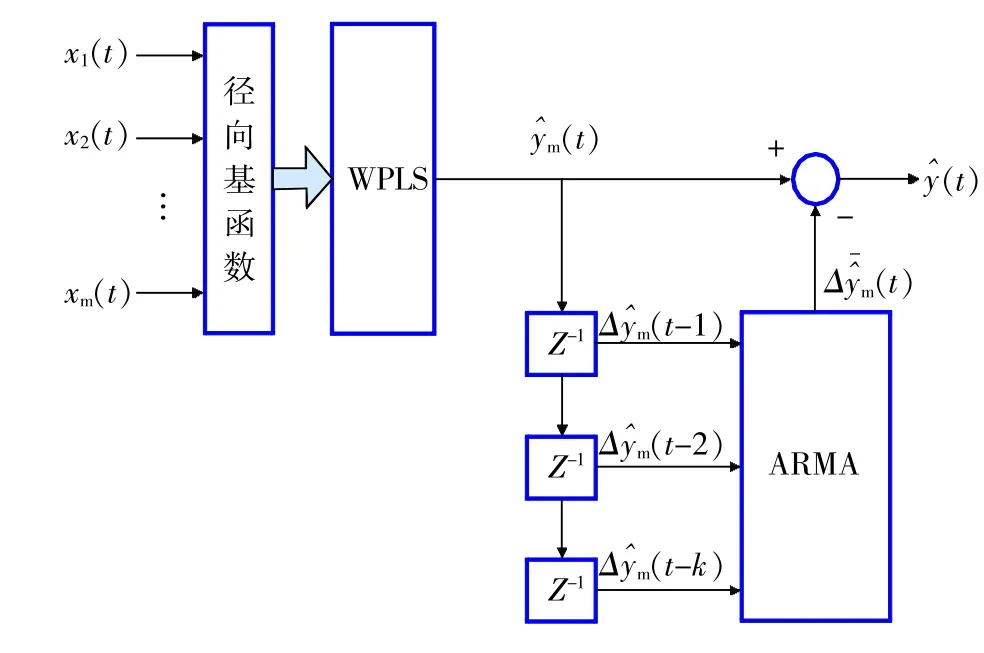
图1 基于RBF-WPLS和ARMA的软测量模型结构

其实现过程步骤如下：

（1）将每个训练样本作为RBF的基向量（ci=xi，i=1，2，…，n），使得隐含层节点个数等于样本数。对输入矢量x执行非线性变换，得到隐含层输出矢量Ri（x）（i=1，2，…，n），即

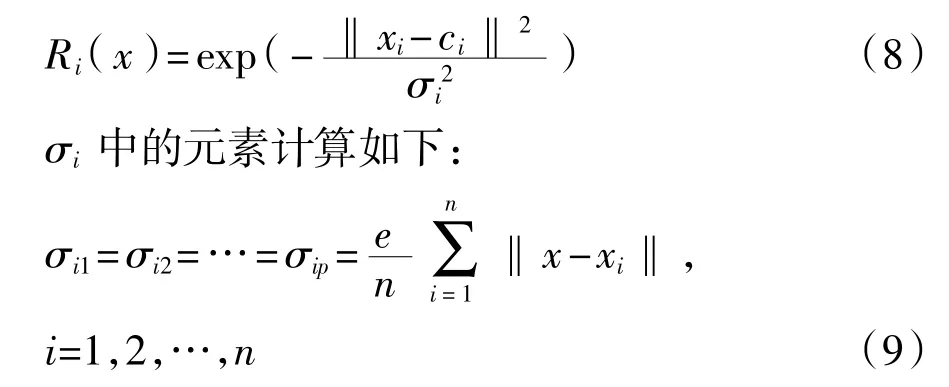
式中：e——大于0的常数。

将得到的输出矢量Ri（x）组成n×n维的隐含层输出矩阵Ri（x）。

（2）采用WPLS回归方法，假定提取的主元个数为t（t=1，2，…，p）；权值分配参数为m（m=t+1，t+2，…，n-1）。

（3）利用舍一交叉验证的思想，在所有样本n中选出一个样本来，设为xi（i=1，2，…，n）。将其作为测试样本，剩余n-1个样本均作为训练样本。并且在训练集中，将与测试样本距离最近的m个样本权值设为1，其余样本权值设为0。构建权值矩阵W。

（4）分别对自变量矩阵X和因变量矩阵进行加权处理，得到m×p维的自变量矩阵Xm=WX和m×q维的因变量矩阵Ym=WY。

（5）通过NIPALS算法，从自变量矩阵Xm中提取t个主元，构建m×t维隐变量数据矩阵Tm，t同时计算对应的p×t维转换矩阵Um，t和t×q维回归系数矩阵Cm，t。

（6）采用相对误差平方和Em，t来确定m和t的值对于1到n记录每个Em，t的值。其中yˆj为测试样本xj的预测矢量为其第l个分量；yjl为第j个实际测量值。

（7）构建相对误差矩阵R，将每个Em，t值对应输入其中，并在矩阵其他没有对应的位置添入+∞。当误差矩阵中Em，t取最小值时，即为Em，t的最优目标值，对应行列分别记为m0和t0。

（8）对于预测对象，将权值分配参数取为m0，提取的主元个数取为t0，按（2）～（6）步骤建立回归模型。

（9）将训练样本集经过WPLS模型处理后，得到一组模型输出值yˆm，将其与真实测量值ym相减，得到关于训练输出值误差时间序列值Δym，对该时间序列进行ARMA建模，确定ARMA（n，n-1）模型阶数。模型阶数n的确定采用递增系列法逐步逼近，找到最合适的n值。

（10）利用上述两个模型对测试样本进行仿真，软测量模型最终的输出值即为

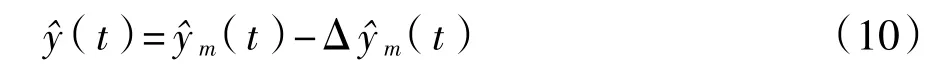
4 仿 真

以某石化公司加氢裂化装置为研究背景，经现场了解工艺情况及相关性分析后发现：航煤干点主要受10个变量的影响：航煤抽出量x1，回流温度x2，回流量x3，轻石脑油抽出量x4，重石脑油抽出点温度x5，重石脑油抽出量x6，进料量x7，进料温度x8，塔釜温度x9，塔顶压力x10。现将10个变量作为模型的输入变量，以分馏塔的航煤干点作为输出变量，对现场数据进行采集，并剔除病态数据，共采集了174组数据。将其中的124组作为训练数据，其余的50组作为测试数据，采用ARMA-RBF-WPLS方法建立航煤干点软测量模型。根据上述ARMA-RBF-WPLS建模步骤，需要寻找Em，t的最小值来确定权值分配参数和主要个数。由趋势性分析得到Em，t取最小值时，分别对应的权值分配参数m为93，主元个数t为8，并选出与预测对象之间欧氏距离最小的93个样本，其权值分配为1，剩余样本权值分配为0，得到加权样本。

ARMA模型参数阶数的确定，从ARMA（2，1）模型开始，以2为步长，建模ARMA模型，每当n增加时，通过F准则去检验判定。当模型增加到ARMA（5，4）时，与ARMA（4，3）对比发现在预定的显著误

差水平上F值下降不显著，所以模型阶数应停止增加，选择ARMA（4，3）为航煤干点的软测量模型。

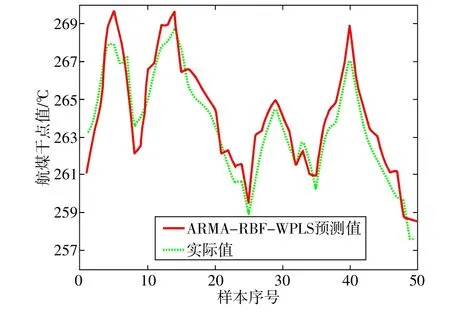
图2 ARMA-RBF-WPLS模型预测结果与实际值对比

图2给出了ARMA-RBF-WPLS模型预测值与工厂实际值对比曲线。

为做对比，采用相同数据用RBF-WPLS方法建立干点预测模型。图3给出了RBF-WPLS模型预测值与工厂实际值对比曲线。从表1和图2～图3可以看出，ARMA-RBF-WPLS模型与RBF-WPLS模型相比，结构更加精确，误差更小，更好地反映了航煤干点的变化趋势。在50组检验样本中，采用ARMA-RBF-WPLS模型的均方差为1.2268℃，82%的样本误差小于±1℃，98%的样本误差小于±2℃；采用RBF-WPLS模型的均方差为1.6514℃，70%的样本误差小于±1℃，90%的样本误差小于±2℃。ARMARBF-WPLS模型与RBF-WPLS模型对比，显示出更高的拟合精度。

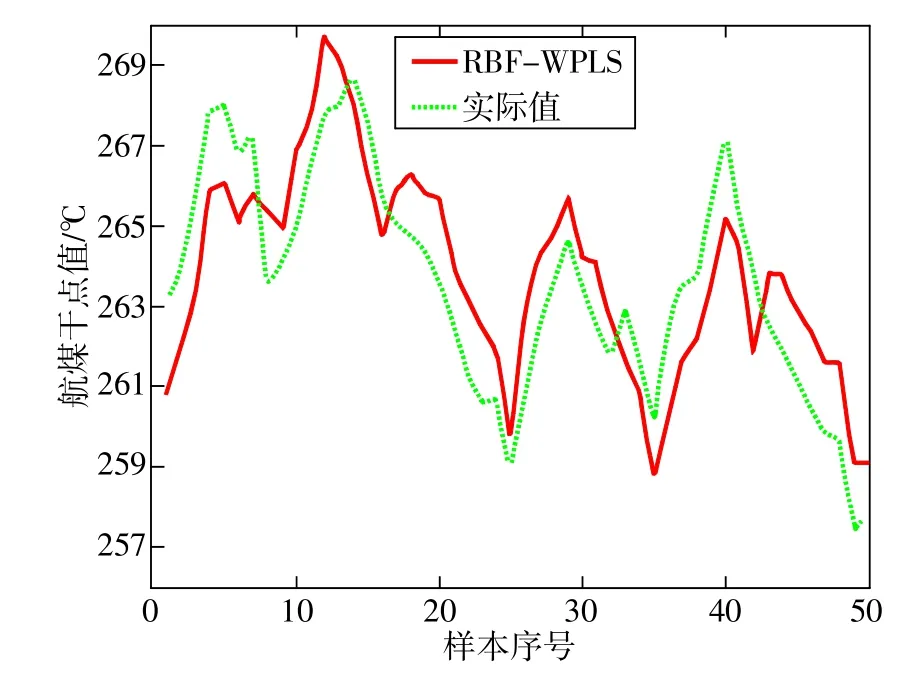
图3 RBF-WPLS模型预测结果与实际值对比

表1 ARMA-RBF-WPL模型和RBF-WPLS模型的结果比较

5 结束语

通过利用RBF-WPLS和AMRA相结合的方法实现了系统动态过程的非线性软测量建模，利用AMRA模型克服了RBF-WPLS算法难以描述动态特性的缺点，利用历史输出值对当前时刻的影响实现了预测误差的动态估计，体现了系统的动态特性。将该方法应用于加氢裂化第一分馏塔航煤干点的预测，仿真结果验证了该方法与RBF-WPLS软测量模型相比具有更高的预测精度。

[1]Bastion P，Esposito V V，Michel T.PLS generalized linear regression[J].Computational Statistics and Data Analysis，2005，48（1）：17-46.

[2]石琳，汤佳佳，于涛，等.基于样条变换的非线性PLS的反应高炉炉温的参数预测[J].钢铁研究学报，2013，25（2）：22-25.

[3]蔡华斌.基于神经网络的电机转矩软测量研究[J].中国测试技术，2007，33（2）：50-52.

[4]Nicolai B M，Theron K I，Lammertyn J.Kernel PLS regerssion on waveler transformed NIR spectra for prediction of sugar content of apple[J].Chemoertrics and Intelligent Laboratory Systems，2007，85（2）：243-252.

[5]颜学峰.基于径基函数-加权偏最小二乘回归的干点软测量[J].自动化学报，2007，33（2）：193-196.

[6]计智伟，吴耿锋.基于层次聚类算法和偏最小二乘的特征选择[J].计算机工程与设计，2009，30（21）：4931-4935.

[7]刘海涛，魏汝禅，蒋国萍.基于加权偏最小二乘回归的软件成本估算方法[J].计算机工程，2012，38（21）：36-39.

[8]贾明兴，赵春晖，王福利，等.基于RBF神经网络的非线性主元分析方法[J].仪器仪表学报，2008，29（3）：453-457.

[9]韩敏，刘晓欣.基于互信息的分布式输入变量选择多元序列预测研究[J].自动化学报，2012，38（6）：999-1006.

[10]阎平凡，张长水.人工神经网络与模拟进化计算[M].北京：清华大学出版社，2000：46-48.

[11]Ives A，Abbott K C，Ziebarth N L.Analysis of ecological time series with ARMA(p,q)model[J].Ecology，2010，91（3）：858-871.

Soft sensing for dry point of jet fuel based on nonlinear dynamic WPLS

ZOU Han
（College of Electronics and Information Engineering，Nanjing Technology University，Nanjing 211816，China）

A nonlinear dynamic modeling method combining auto-regressive and moving average and radial basis function-weighted partial least squares regression is presented to solve the problem according to the requirements for refining industrialprocesses with multivariable，nonlinear and dynamic data.Firstly，this approach built RBF-WPLS model.Then，ARMA models use the data correction timing analysis，and dynamic error message will be added to the model to achieve a dynamic model.Finally，the proposed ARMA-RBF-WPLS was used to predict the dry point of jet fuel in hydrocracking unit，and it obtained highly precise prediction results compared with RBF-WPLS methods.

radial basis function；ARMA model；partial least square；dry point；soft sensor

TP273；TE62；O224；O241.5

：A

：1674-5124（2014)03-0121-04

10.11857/j.issn.1674-5124.2014.03.032

2013-11-16；

：2014-01-22

邹 涵（1990-），男，江西丰城市人，硕士研究生，专业方向为复杂过程的先进控制。