基于序贯算法的无偏最小二乘估计纯方位目标跟踪

尚 进, 李亚安, 蔚 婧, 李晓花



基于序贯算法的无偏最小二乘估计纯方位目标跟踪

尚 进, 李亚安, 蔚 婧, 李晓花

(西北工业大学 航海学院, 陕西 西安, 710072)

测量方程的非线性是纯方位角跟踪研究的难点。为了解决传统伪线性估计结果存在严重有偏性这一问题, 提出了一种基于伪线性估计的无偏估计方法, 即在伪线性方程中利用约束最小二乘估计, 它不需要对初始值进行假设, 且收敛效果良好。采用序贯滤波方法对估计量作批处理滤波以减少运算量, 提高了运算效率。仿真结果表明, 利用该方法得到的估计量在高斯噪声下能很好地逼近理想状态, 且收敛速度较快, 比扩展卡尔曼滤波具有更好的跟踪精度及收敛速度, 在目标高速运动时仍能保持较好的跟踪效果。

纯方位; 伪线性估计; 约束最小二乘; 序贯算法; 无偏估计

0 引言

纯方位目标跟踪(bearing-only tracking, BOT)在过去几十年中一直是研究的重点与难点[1-6]。BOT属于典型的被动跟踪, 为目标跟踪领域的一个重要分支。它是在被动测量的情况下, 仅仅利用目标的方位信息, 估计目标运动参数的过程。测量方程的非线性是纯方位角跟踪研究的重点与难点。Lindgern和Gong[1]提出伪线性估计(pseudo- linear estimation, PLE)来解决这一问题, 然而加了噪声的观测量会出现在测量矩阵中, 从而导致严重的偏差[7]。

为克服偏差所带来的影响, Aidala和Hammel提出了修正极坐标的纯方位目标跟踪[8], 结果显示, 所估计的状态向量在修正极坐标下呈渐进无偏。Passerieux[9]和Chan[7]利用辅助变量(ins- trumental variable, IV)算法, 理论上可以消除偏差, 然而关键的问题是如何选取合适的辅助变量。另一种消除偏差的方法是最大似然估计(maximum likelihood estimator, MLE)[10]。此方法使用梯度搜索, 但是收敛效果取决于给定的初始条件和步长的选取[2, 11]。经典算法中, 广泛应用的是扩展卡尔曼滤波(extended Kamlman filter, EKF)[12], 但可能存在协方差崩溃的现象, 且EKF对于初值十分敏感, 容易产生无法收敛的结果。

1 纯方位目标运动问题描述

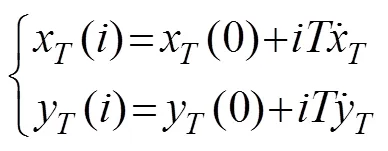
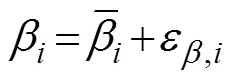
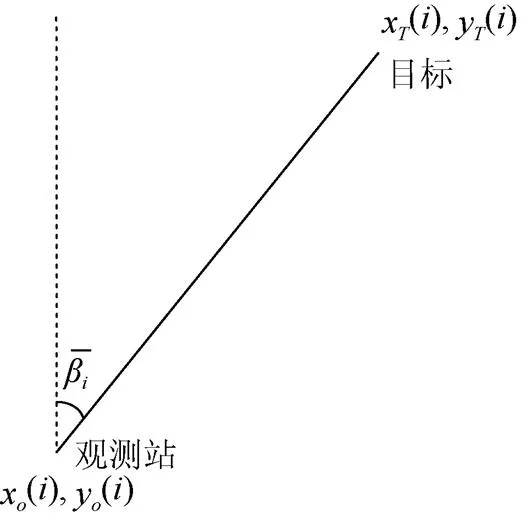
图1 观测角度, 观测站及目标位置示意图

交叉相乘得

测量向量

测量矩阵

2 最小二乘无偏估计方法

把式(11)和式(12)带入式(5),得

其中

首先, 定义一个增广测量矩阵

和一个增广解向量

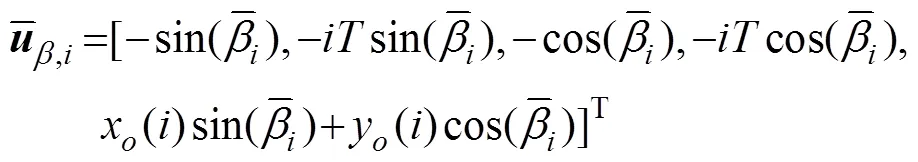
则

其中

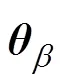
用拉格朗日乘数法可以解决约束条件最小化的问题[2]。构造辅助代价函数

3 序贯估计算法

由式(6), 式(7)和式(18)得

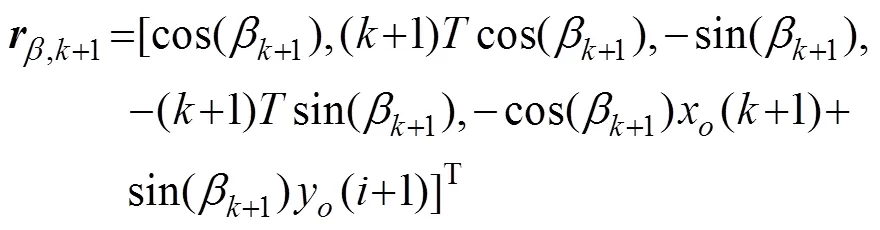
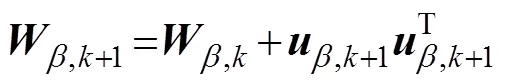
4 仿真结果与分析

4.1 假设观测站和目标均为潜艇

图2 目标与观测站位置示意图

Fig. 2 Schematic of positions of target and observer

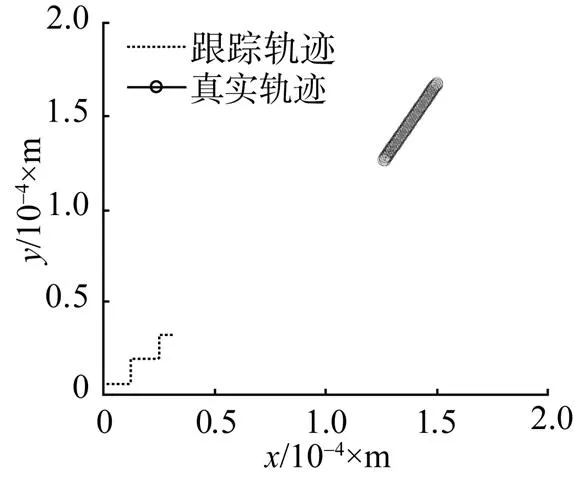
图3 观测噪声= 1°时潜艇-潜艇跟踪轨迹示意图

Fig. 3 Schematic of trajectory of a submarine tracking target submarine when observing noise=1°

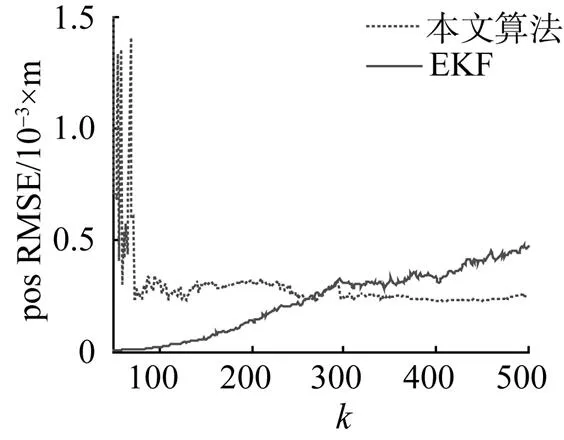
图4 s =1°时潜艇-潜艇位置估计均方根误差

图5 s =2°时潜艇-潜艇位置估计均方根误差

图6 s =1°时潜艇-潜艇速度估计均方根误差

图7 s=2°时潜艇-潜艇速度估计均方根误差

4.2 假设观测站为潜艇和目标为高速运动鱼雷

图8 s =1°时潜艇-鱼雷跟踪轨迹

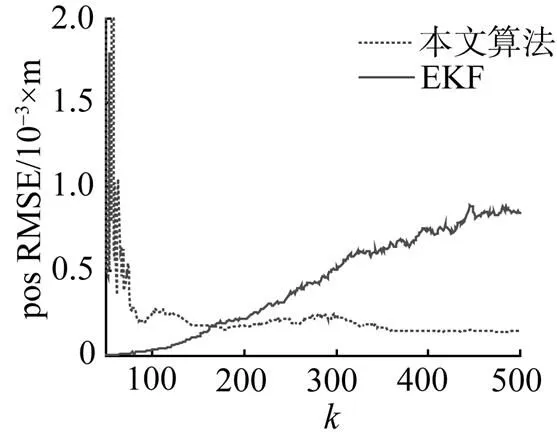
图9 s =1°时潜艇-鱼雷位置估计均方根误差

图10 s =2°时潜艇-鱼雷位置估计均方根误差

图11 s =1°时潜艇-鱼雷速度估计均方根误差

图12 s =2°时潜艇-鱼雷速度估计均方根误差

仿真中由于先以前50个采样点作为一组数据得到初始化的值, 再进行序贯估计, 故得到初始值之前的前50个计算数值与误差较大, 得到仿真初值后再滤波, 误差则趋于稳定。

5 结束语

本文对于匀速直线运动的目标提出了一种无偏估计方法。此方法利用在约束条件下的最小二乘估计算法, 使得结果呈现无偏, 并且不需要假设初始值。当有新的测量值时, 序贯估计方法用来更新解向量。当在开始计算出一个解时, 序贯算法不需要在随后的每一步估计中再进行广义特征值分解, 这样大大提高了计算的效率。与EKF 算法相比, 本文算法在位置和速度均方根误差精度上, 都有很大的提高, 并且收敛速度更快, 对高速运动目标的跟踪仍有良好的可靠性。

[1] Lindgren A G, Gong K F. Position and Velocity Estimation via Bearing Observations[J]. IEEE Transactions on Aerospace and Electronic Systems, 1978, 14(4): 564-577.

[2] Ho K C, Chan Y T. An Asymptotically Unbiased Estimator for Bearings-Only and Doppler-Bearing Target Motion Analysis[J]. IEEE Transactions on Signal Processing, 2006, 54(3): 809-821.

[3] 顾晓东, 袁智勇, 邱志明. 基于辅助变量法的双基阵纯方位目标跟踪算法[J]. 系统工程与电子技术, 2010, 32(3): 508-511.

Gu Xiao-dong, Yuan Zhi-yong, Qiu Zhi-ming. Bistatic Bearing-only Target Tracking Algorithm Based on Instrumental Variable Method[J]. Systems Engineering and Electronics, 2010. 32(3): 508-511.

[4] 刘忠, 周丰, 石章松, 等. 纯方位目标运动分析[M]. 北京: 国防工业出版社, 2008.

[5] 郭云飞. 纯方位角目标跟踪理论与应用研究[D]. 浙江: 浙江大学, 2007.

[6] Nardone S C, Aidala V J. Observability Criteria for Bearings-only Target Motion Analysis[J]. IEEE Transactions on Aerospace and Electronic Systems, 1981, 17(2): 162- 166.

[7] Chan Y T, Rudnicki S W. Bearings-only and Doppler-bearing Tracking Using Instrumental Variables[J]. IEEE Transactions on Aerospace and Electronic Systems, 1992, 28(4): 1076- 1083.

[8] Hammel S E, Aidala V J. Utilization of Modified Polar Coordinates for Bearings-only Tracking[J]. IEEE Transactionson Automatic Control, 1983, 28(3): 283-294.

[9] Passerieux J M, Pillon D, Blanc-Benon P, et al. Target Motion Analysis with Bearings and Frequencies Measurements via Instrumental Variable Estimator[C]//IEEE International Conference on Acoustics, Speech and Signal Processing,1989, 2645-2648.

[10] Tao X J, Zou C R, He Z Y. Passive Target Tracking Using Maximum Likelihood Estimation[J]. IEEE Transactions on Aerospace and Electronic Systems, 1996, 32(4):1348- 1354.

[11] Cadre J P, Le, Jauffret C. On the Convergence of Iterative Methods for Bearings-only Tracking[J]. IEEE Transactions on Aerospace and Electronic Systems, 1999, 35(3): 801-818.

[12] Aidala V J. Kalman Filter Behavior in Bearings-only Tracking Applications[J]. IEEE Transactions on Aerospace and Electronic Systems, 1979, 15(1): 29-39.

(责任编辑: 杨力军)

Unbiased Least Square Estimation for Bearings-Only Target Tracking Based on Sequential Algorthm

SHANG JinLI Ya-anYU JingLI Xiao-hua

(College of Marine Engineering, Northwestern Polytechnical University, Xi′an 710072, China)

Bearings-only target tracking attempts to obtain a target trajectory only based on bearings measurements. This problem is difficult because the measurement equations are nonlinearly related to the target parameters. The pseudolinear estimation provides a linearized measurements equation, however the estimation result is severely biased. In order to deal with this problem, this paper proposes an unbiased estimation method with good convergence property, in which constraint least squares minimization is applied to the pseudolinear estimation without assuming initial values. The sequential filtering algorithm is employed for batch processing of the estimator, thus the estimation accuracy is improved and the computation is reduced. Simulation result shows that the proposed algorithm gets higher tracking accuracy and faster convergence speed than the extended Kalman filter, the obtained estimator approaches the perfect state in the condition of Gaussian noise rapidly and keeps steady when the target is moving at a high speed.

bearings-only; pseudolinear estimation; constraint least squares; sequential algorithm; unbiased estimation

TJ630.34

A

1673-1948(2014)01-0020-06

2013-06-06;

2013-09-01.

国家自然科学基金(51179157).

尚 进(1989-), 男, 在读硕士, 主要研究方向为水下目标跟踪.