基于EMD和Gabor变换的发动机曲轴轴承故障特征提取*
2014-02-27赵红东张玲玲肖云魁赵慧敏
沈 虹,赵红东,张玲玲,肖云魁,赵慧敏
(1.河北工业大学信息工程学院,天津 300401;2.军事交通学院基础部,天津 300161;3.军事交通学院汽车工程系,天津 300161)
前言
柴油机运转包含复杂的往复运动和旋转运动,其振动信号由不同激励源激发的信号成分叠加而成,因此缸体的振动信号是典型的非平稳信号,频率成分复杂[1]。对于非平稳信号,如果将其看作平稳信号直接进行频谱分析将产生严重的“频率模糊”,从而导致较大的误差甚至错误[2]。Wigner-Ville分布、短时Fourier变换等时频分析方法在不同程度上描述了非平稳信号的时变性,但基函数的选择不是自适应的,且样本多时存在计算量大、速度慢的问题。如何从非平稳且含有强烈的背景噪声的振动信号中提取出故障特征信息是轴承故障诊断的关键。
文献[3]中提出的经验模态分解(empirical mode decomposition,EMD)方法是一种新的具有自适应性的时频分析方法,可根据信号的局部时变特性进行自适应的时频分解,非常适合于非线性、非平稳信号,该方法已成功应用于机械故障诊断领域[4-8]。轴承发生故障时,在相同频带内的信号频率分布会发生改变。由于背景噪声的影响,故障频率往往不明显。故可通过计算本征模态函数(intrinsic mode function,IMF)分量的相关性,选择相关性强的IMF分量,也即对占信号能量主要部分的分量进行变换和分析,从而降噪和突显故障特征。
Gabor变换是一种时频变换,可同时提供时域和频域局部化的信息,将Gabor变换与EMD方法相结合,能有效解决发动机故障诊断的特征提取问题。
本文中采用EMD与Gabor变换时频分析相结合的方法,用EMD方法对曲轴轴承不同技术状况下的振动信号进行分解,得到各阶IMF分量,选择与原始信号相关性强即占信号主要成分的IMF分量进行Gabor变换,由时频分布图得到频带能量累加曲线,分析频带能量随曲轴轴承不同间隙的变化情况,提取曲轴轴承的故障特征。
1 经验模态分解
EMD方法在本质上是对一个信号进行平稳化处理,其结果是将信号中不同尺度的波动或趋势逐渐分解出来,产生一系列具有不同特征尺度的数据序列,每一个序列称为一个IMF分量[9]。EMD方法的具体过程如下。
(1) 确定信号x(t)的所有局部极值点,通过三次样条函数求取其上包络u1(t)和下包络u2(t)的局部均值:
(1)
(2) 令h(t)=x(t)-m(t),如h(t)不满足IMF条件,则视其为新的x(t),重复k次得
h1k(t)=h1(k-1)(t)-m1k(t)
(2)
现实中过多地重复上述处理会使IMF变成幅度恒定的纯粹的频率调制信号,从而失去实际意义。因此,可采用标准差SD(一般取0.2~0.3)来作为筛选过程停止的准则。
(3)
(3) 得到信号的第1个IMF分量C1=h1k(t)及其分离后的余项r1(t)=x(t)-C1。
(4) 将r1(t)进行同样的“筛选”过程,依次得到C2,C3,…,直到ri(t)基本呈单调趋势或很小时停止,则原信号重构为
(4)
式中:余项rn(t)为信号的平均趋势;IMF分量Ci(t)为信号的固有的谐波成分。
与小波分析相比,EMD更易获得不同时间尺度的信号特征,同时这些不同时间尺度的信号实际上是对故障信号线性和平稳化处理的结果,这也为Gabor变换的引入提供了技术基础。
2 Gabor变换
由于经典Fourier变换只能反映信号的整体特性,而Gabor变换可以达到时频局部化的目的。Gabor变换定义为
(5)
信号的重构表达式为
(6)
式中:ga(t)为高斯函数;a、b为参数,且a>0,b>0。参数b用于平行移动窗口,以便于覆盖整个时域。高斯函数的Fourier变换仍为高斯函数,这使得Fourier逆变换体现了频域的局部化。Gabor变换是最优的窗口Fourier变换,能在整体上提供信号的全部信息,又能提供在任一局部时间内信号变化剧烈程度的信息。
3 试验与分析
3.1 试验设置
以EQ2102型柴油机作为试验对象,设置第3缸前后两道曲轴轴承为故障轴承,试验时在其它条件均不变的情况下,仅改变曲轴轴承的配合间隙。分别设置曲轴轴承的配合间隙为0.08mm(正常间隙)、0.20mm(轻微磨损)和0.40mm(严重磨损)。为了比较不同的测点位置对特征提取的影响,试验中设置了多个测试点,如图1所示。将加速度传感器分别放置在第3缸对应的缸体顶部(图中,a1位置)、缸体上部左侧(a2位置)、右侧(b1位置)、油底壳与缸体结合处左侧(b2位置)、右侧(c1位置)和油底壳下部(c2位置)6个测点。
在加速或减速过程中,发动机机械故障现象的表现更明显。这是因为在非稳态运转条件下,运动部件产生更剧烈的激励。因此,采用定转速触发方式采集发动机加速振动信号。所谓定转速触发采集,就是设定一个转速值,一旦发动机达到这个转速值,采集器开始采集信号。设定采集器触发转速分别为800,1 300,1 800和2 100r/min,分别对应于发动机怠速、怠速稍高、中速和中速稍高4种状态,采样频率为25.6kHz,采样点数为8 192,采集上述3种技术状况下的发动机振动信号。图2为触发转速1 800r/min,传感器位于右侧位置,曲轴轴承间隙为0.40mm时的振动信号。图3为触发转速1 800r/min,右侧位置,不同配合间隙的振动信号频谱图。由图可见:随着曲轴轴承间隙的增加,信号低频部分的能量减少,高频部分的能量增大;但在频谱图中,频率成分较复杂,不易提取出反映曲轴轴承故障程度的特征。
3.2 发动机非稳态信号的EMD分解与Gabor变换
采用EMD方法对所测得的柴油机曲轴轴承振动信号进行分解得到若干IMF分量,工况不同其IMF分量数目和各阶模态有所不同。图4为触发转速1 800r/min,油底壳位置,正常配合间隙时的信号EMD分解结果。
计算出各个分量与原信号的相关系数分别为0.577 9,0.638 5,0.440 1,0.202 5,0.093 6,0.012 0,0.014 1,0.003 4,-0.002 4,-0.000 2,可以看出,第5阶以后,IMF分量与原始信号的相关性已经非常小。这是因为故障时柴油机振动信号的故障信息在中高频段且前几个IMF分量包含了信号的主要能量,因此选取前4阶IMF分量,分别对前4阶IMF分量进行Gabor变换,即把与原始信号不相关的噪声分量滤除,只对占原始信号主要成分的分量进行分析。分别对各阶IMF分量进行Gabor变换,得到其时频分布三维图。图5为触发转速1 800r/min,油底壳位置,正常配合间隙时的信号EMD分解第2阶分量Gabor变换时频分布图。为了便于分析,定义“频带能量累加曲线”这个概念,就是在时频三维图上,对时间轴进行累加,得到幅频特性曲线。以图5为例,将频率为0对应的时间轴上从0到0.32s的所有点的幅值累加得到频率为0时的能量累加值,依次计算频率轴上所有频率点的能量累加值则得到频带能量累加曲线,即幅频特性曲线。在非稳态信号分析中,它能显著提高分析结果的稳定性。图6为对触发转速1 800r/min,油底壳位置处的信号前4阶IMF分量进行Gabor变换后的频带能量累加曲线,相同位置相同转速不同配合间隙的3个同阶IMF分量为一组。
从前4阶IMF分量的频带能量累加曲线上可以看出,阶数相同的IMF分量所包含的频带中心频率大致相等,而阶数不同的IMF分量,随着阶数的增加,频带范围由高频到低频,每个IMF分量对应于信号的某个频带范围。计算各阶IMF分量所包含的频带能量,如表1所示。由表可见:第1阶IMF分量的能量随配合间隙增大而增大,幅度分别为76.77%和46.63%,而其余各阶分量能量与配合间隙关系不大,因此可以此作为判断曲轴轴承磨损的特征参数。

表1 各阶IMF分量能量随故障程度的变化情况
3.3 试验结果分析
按前述方法采集发动机振动信号,对不同转速和配合间隙的振动信号进行EMD分解,得到每个信号的各阶IMF分量。相同位置相同转速不同配合间隙的3个同阶IMF分量为一组。分析每组信号Gabor变换后频带能量累加曲线上随配合间隙增大而频带能量增大的IMF分量,找出可选的触发转速和测量位置,结果如表2所示。表中内容为对应的触发转速和位置下可选做故障特征的IMF分量阶数,传感器位置见图1。例如表中1 800r/min,c2位置为1代表图6中触发转速1 800r/min,油底壳位置的第1阶IMF分量的频带能量可以作为故障特征。
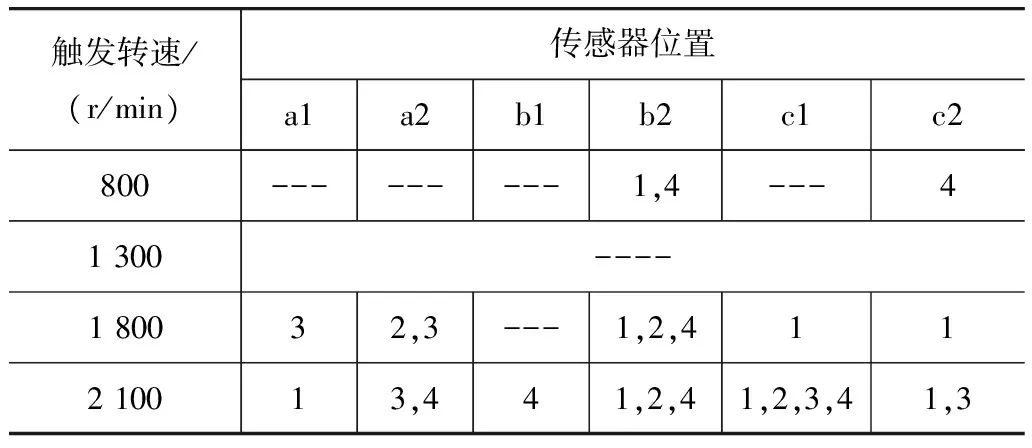
表2 可选做故障特征的IMF分量及其对应的触发转速和传感器测量位置
注:---表示无规律
由表可见:总的趋势是,发动机触发转速越高,可选做特征参数的IMF分量越多,如c1位置,随着触发转速的增高,触发转速为800和1 300r/min时,没有可选的IMF分量,触发转速为1 800r/min时,可选的IMF分量为1阶,触发转速为2 100r/min时,可选的IMF分量为1,2,3,4阶。以第3阶为例,表3示出其能量随间隙的变化情况。由表可见,随着配合间隙的增大,b2,c1,c2处频带能量增大的趋势比a1,a2,b1处明显。这是因为不同的测量位置,信号的传递路径不同,相当于不同的滤波过程,会引入不同的干扰和噪声,而a1,a2,b1位置由于距离激励源较远,信号的故障特征淹没在大量噪声干扰中,不能很好地显现。另外,c1位置略好于b2处,这是由于从面对车头的方向观察(见图1)发动机运转时,连杆带动曲轴做顺时针旋转运动,当被测轴承对应的气缸开始做功时,连杆带动曲轴对轴承右侧形成瞬态强烈冲击,位于缸体外部右侧的振动传感器正好捕捉到这一信息;当曲轴撞击轴承左侧时,气缸已完成做功行程,撞击已经明显减弱;当触发转速为2 100r/min,传感器位于c2位置时,可选的IMF分量的频带能量随轴承配合间隙的增大而急剧增大,最能反映曲轴轴承磨损故障,因此可以作为诊断的最佳触发转速和最佳测量位置。
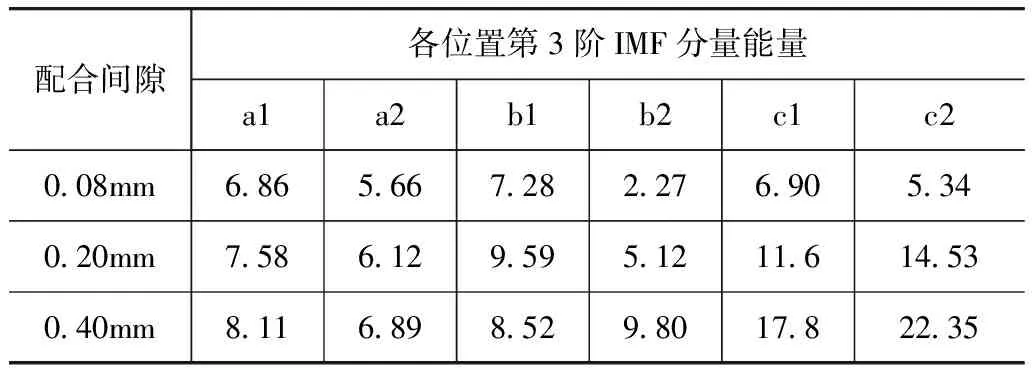
表3 触发转速2 100r/min各个位置第3阶IMF分量能量随故障程度的变化情况
4 结论
(1) 发动机曲轴轴承振动信号具有非平稳性,且常常会受到各种背景噪声的干扰,故障信息难以直接提取。EMD分解后所得的IMF分量突出了原信号不同的局部特征信息,有利于故障特征提取。
(2) 采用EMD分解和Gabor变换相结合的方法,从IMF分量的频带能量累加曲线上能有效地提取被噪声掩盖的故障特征参数。诊断故障简单而有效,避免了采用其它谱分析方法计算数据庞大、计算数据点数有限的缺陷。
(3) 诊断的最佳触发转速为2 100r/min,其次为1 800r/min,最佳位置为油底壳处,其次为缸体与油底壳结合处左右两侧。
[1] 肖云魁.汽车故障诊断学[M].北京:北京理工大学出版社,2006.
[2] 赵晓平,张令弥,郭勤涛.旋转机械阶比跟踪技术研究进展综述[J].地震工程与工程振动,2008,28(6):213-214.
[3] Huang Norden E,Shen Zheng,Long Steven R,et al.The Empirical Mode Decomposition and the Hilbert Spectrum for Nonlinear and Non-stationary Time Series Analysis[J].Proc.R.Soc.Lond.A,1998,454:903-995.
[4] 张超,陈建军,徐亚兰.基于EMD分解和奇异值差分谱理论的轴承故障诊断方法[J].振动工程学报,2011,24(5):539-545.
[5] 吴虎胜,吕建新,战仁军,等.基于EMD和AR奇异值的柴油机故障诊断[J].机械设计与制造,2011,4(4):230-232.
[6] 夏天,王新晴,肖云魁,等.应用EMD-AR谱提取柴油机曲轴轴承故障特征[J].振动、测试与诊断,2010,30(3):318-321.
[7] 张玲玲,廖红云,曹亚娟,等.基于EEMD和模糊C均值聚类算法诊断发动机曲轴轴承故障[J].内燃机学报,2011,29(4):332-336.
[8] 李辉,郑海起,唐力伟.基于EMD和功率谱的齿轮故障诊断研究[J].振动与冲击,2006,25(1):133-136.
[9] 蔡艳萍,李艾华,王涛,等.基于EMD-Wigner-Ville的内燃机振动时频分析[J].振动工程学报,2010,23(4):430-437.
