汽车防抱死制动系统的H∞鲁棒控制*

2014-02-27严运兵

汽车工程 2014年4期

严运兵，吴浩，赵慧

(1.武汉科技大学汽车与交通工程学院，武汉 430081； 2.郑州宇通客车股份有限公司新能源技术部，郑州 450061；3.武汉科技大学机械自动化学院，武汉 430081)

前言

汽车防抱死制动系统(ABS)是一种主动安全装置。它从防止制动过程中车轮抱死的角度出发，避免车辆后轮侧滑和前轮丧失转向能力，提高车辆对地面附着系数的利用率，从而达到改善车辆制动稳定性、操纵性和缩短制动距离等目的。

ABS控制方法是其核心技术，因易实现连续控制，提高ABS在制动过程中的平顺性，并最大限度地发挥其制动性能，故以滑移率为控制目标的各种ABS控制方法成为了研究的热点[1-2]。文献[3]中以滑移率为控制目标，设计了ABS系统的PID控制器，且能基本达到控制要求。文献[4]和文献[5]中设计了基于闭环增益成形算法的鲁棒控制器，对确定系统的控制较为有效。

ABS系统在实际使用时，往往会因为外界的扰动(如汽车载人数量或载货质量的变化，制动器因磨损导致的效能下降和轮胎气压与路面条件等因素的变化)，而使被控系统存在不确定性。这就需要在考虑不确定性的基础上，设计出能在一定程度上抑制扰动的鲁棒控制器。据此，本文中以滑移率为控制目标，通过对ABS数学模型的建立和简化，对ABS系统进行混合灵敏度H∞鲁棒控制设计，以期实现控制系统对不确定性参数摄动的抑制，提高制动的鲁棒性能。

1 ABS数学模型及其简化

汽车ABS系统的数学模型由车辆动力学、轮胎、制动系统和滑移率计算4部分模型组成。

1.1 车辆动力学模型

在不考虑复杂因素的情况下，单轮车辆模型的结构简单，适合于汽车防抱死制动系统性能的分析，如图1所示。车辆的动力学方程如下。

车辆运动方程：

(1)

车轮运动方程：

(2)

车辆纵向摩擦力：

Fx=μN

(3)

式中：M为分配到车轮上的汽车质量；R为车轮滚动半径；I为车轮转动惯量；Tb为制动转矩；v为车辆速度；ω为车轮角速度；Fx为车轮和地面的摩擦力；μ为车轮与地面间的纵向附着系数；N为车轮所受的垂向载荷，N=Mg。

1.2 轮胎模型

轮胎模型是指制动过程中轮胎附着力和其它各种参数之间的函数关系式，通常用轮胎附着系数与各种参数的函数关系来表示。本文中采用比较常用且相对精确的魔术公式来描述轮胎模型[6]。用魔术公式模型来模拟制动时车轮纵向附着系数和车轮滑移率之间的关系，即

μ(S)=f+D·sin{C·arctan[B·S-E·(B·S-

arctan(B·S))]}

(4)

式中：S为滑移率；f相当于车轮在纯滚动时的附着系数，一般情况下设为0；D、C、B、E都是与路面有关的常数，通过改变这些参数可模拟不同路面的附着系数。

1.3 制动系统模型

制动系统模型包括驱动机构模型和制动器模型两部分。目前，ABS的驱动机构一般采用电液控制，即用电磁阀来调节制动系统的工作压力。为了使系统简化，忽略电磁阀中弹簧等元件的非线性特性及压力传送的延迟，将驱动机构简化为1阶惯性环节。

(5)

式中：p为制动缸压力，MPa；p0为初始制动压力，MPa；Tp为时间常数；s为拉普拉斯变换算子。

制动器模型指制动转矩Tb与制动轮缸压力p之间的关系模型。为便于对控制过程进行仿真，假设制动器为理想元件，认为其非线性特性较弱并忽略其滞后带来的影响。因此，制动器模型为

Tb=Ktp

(6)

式中Kt为制动器效能因数。

1.4 滑移率计算模型

汽车制动时，如果车轮线速度低于汽车行驶速度，轮胎和路面之间将产生滑移，此时滑移的程度常用滑移率表示[7]，其计算公式为

(7)

1.5 ABS数学模型简化

借鉴文献[4]的模型简化方法，对ABS系统数学模型进行简化。得到系统的状态方程为

(8)

输出方程为

(9)

汽车模型的仿真参数如表1所示。

代入仿真参数，将式(8)和式(9)转换成传递函数形式，得系统的传递函数为

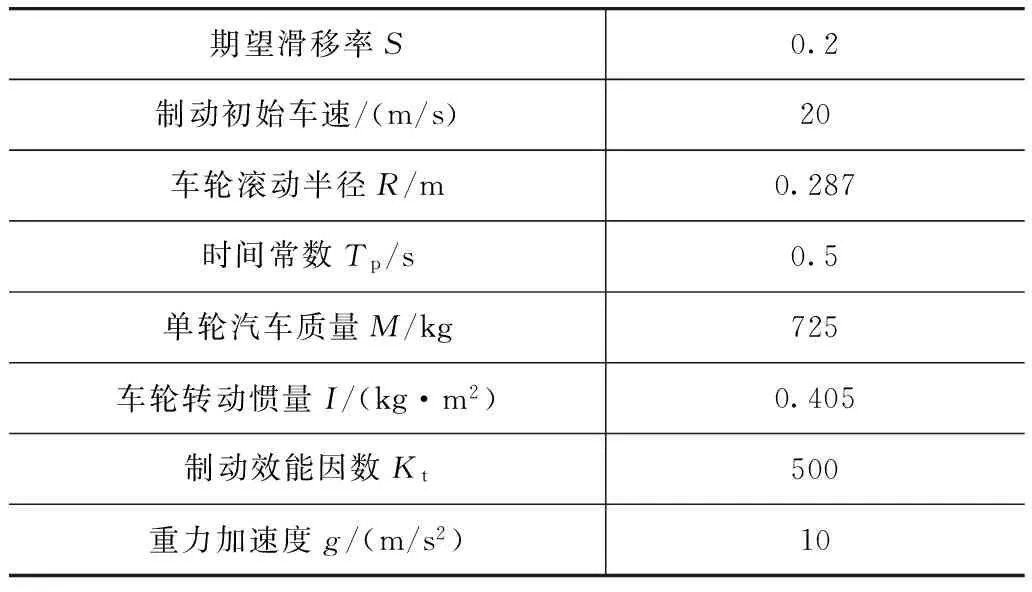
表1 汽车模型仿真参数

(10)

2 ABS的H∞鲁棒控制设计

2.1 H∞混合灵敏度鲁棒控制方法

H∞鲁棒控制理论是在H∞空间(即Hardy空间)通过对性能指标的无穷范数进行优化而获得具有鲁棒性能的控制器的一种理论。当利用被控系统的数学模型G来设计控制器时，由于参数的变化和不确定性，并为便于设计与计算，往往把对象的模型简化，导致对象的数学模型G存在误差ΔG。H∞控制的目的是：利用标称模型G来设计控制器K，使K在稳定被控对象的同时使某一目标函数P的H∞范数最小[9]：

γ=min‖P(s)‖

混合灵敏度问题是H∞控制的最典型问题之一，在应用H∞方法设计系统时，为保证鲁棒性和提高系统性能，通常将设计问题转化为混合灵敏度问题。混合灵敏度设计系统如图2所示。其中r、e、n、d和y分别表示参考输入、跟踪误差、测量噪声、干扰输入和系统输出。W1、W2和W3为分别对应于系统性能、控制器输出约束和鲁棒性的权值。

设从r到e、u、y的传递函数分别为

U=(I+GK)-1

(11)

V=K(I+GK)-1

(12)

Q=GK(I+GK)-1

(13)

式中：U和Q分别为灵敏度函数和补灵敏度函数。则H∞混合灵敏度控制就是指在频域内选择加权函数W1、W2、W3，使之满足：

(14)

2.2 加权函数的选择

加权函数的选择是H∞混合灵敏度设计问题中关键的一步。加权函数选择的合适与否直接影响设计系统的性能。H∞混合灵敏度控制的设计过程在很大程度上是对U、V、Q的加权函数的选择过程。在选择和验证加权函数时必须满足下列关系，作为加权函数的选择依据[10-11]。

① 灵敏度函数U是闭环系统对干扰抑制的度量，由式(10)可得：

② 若加性摄动Δa和乘性摄动Δm满足：

则有：

④ 在低频区有：

U=(1+GK)-1≈(GK)-1

V=KU≈G-1

Q=GKU≈I

在高频区有：

U=(1+GK)-1≈I

V=KU≈K

Q=GKU≈GK

⑤ 对于幅值裕量GM和相位裕量θM有：

上述关系中，关系④最直观且最易操作，因此本文中以关系④为主要原则来选取加权函数，并在此基础上对其他几个关系进行检验。

2.3 ABS系统中加权函数的选择

由式(10)可知，ABS系统的标称模型是一个2阶模型。据此可进行加权函数的选择[11]。

W1由系统的性能要求决定，通常应具有积分特性或高增益低通特性。一般取W1(s)=k1/(s/ω1+1)。调整k1可有效扩展系统频宽，调整ω1可有效抑制系统超调量。为满足系统的频宽要求，获得理想动态过程，通过仿真，取W1(s)=100/(s+1)；W2由系统参数的摄动范围决定，也可用来约束控制器的输出。混合灵敏度设计中可通过对加权阵W2的选取来实现对控制信号幅值的约束。为了不增加控制器的阶次，通常取W2为一常数k2。为了约束控制器的输出，保证系统频宽的要求，取W2=0.000 05；W3可根据系统的高频未建模动态来选取。W3一般具有高通性质，且W1和W3的频带不能重叠。W3的阶次不宜取得太大，否则将影响迭代速度和控制器的阶数，一般取W3(s)=k3s/(s/ω3+1)。W3也影响系统频宽，通常ω3越大，系统的频宽越宽。k3越大系统频宽越窄。为满足高通性质，并保证系统频宽要求，通过仿真实践，取W3(s)=s/(s+1 000)。

2.4 H∞控制器求解和ABS系统仿真

本文中使用Matlab软件中的鲁棒控制工具箱进行H∞鲁棒控制设计，可大大减少计算量，只须进行加权函数的选择[12]。

在Matlab环境下，对ABS系统的标称模型进行加权，并使用hinf命令求解H∞鲁棒控制器[13-15]，结果为一个4阶模型：

3 仿真与结果分析

3.1 鲁棒控制仿真

利用Matlab/Simulink工具建立ABS仿真模型，将求解得到的K(s)作为ABS的鲁棒控制器进行仿真，可得到单轮车辆模型基于H∞鲁棒控制的ABS系统动态仿真响应过程。

图3和图4分别给出了ABS系统在鲁棒控制器K(s)作用下轮速、车速与制动距离的仿真结果和滑移率曲线。从图3可以看出，在使用该ABS系统后，车速和轮速都在不断减小，最后同时减为0，表明当汽车制动停止时车轮才抱死，提高了制动过程中的操纵稳定性，真正起到了制动防抱死的作用。从图4可以看出，整个制动过程中，车轮滑移率基本上在期望滑移率附近变化，表明车轮充分利用了最大的地面附着力，获得了较大制动力，从而使汽车能在最短距离内停车。

3.2 鲁棒控制与传统PID控制的对比

图5和图6给出了基于传统PID控制的轮速、车速与制动距离仿真结果和滑移率曲线。对比图3和图5，基于传统PID控制的车速和轮速变化曲线不如鲁棒控制的平滑，说明鲁棒控制的稳定性更好；对比图4和图6，基于传统PID控制的滑移率曲线需要一定的响应时间，且在制动结束时产生了振动，而鲁棒控制的滑移率曲线则一直保持平滑，说明PID控制的控制精度、响应时间和鲁棒稳定性都不如鲁棒控制。

3.3 参数变化对鲁棒控制仿真结果的影响分析

图7和图8给出了汽车载质量改变后的仿真结果和改变前后滑移率变化的对比曲线，目的是验证控制系统的鲁棒性能。对比图3和图7，仿真结果变化不大。从图8可以看出，当汽车质量从725kg增加至1 000kg时，滑移率曲线变化很小，始终保持在0.19～0.20的区间内，表明该控制系统不仅能达到较高的控制精度，而且系统的鲁棒稳定性很好。

图9和图10给出了汽车制动效能因数改变后的仿真结果和改变前后滑移率变化的对比曲线。对比图3和图9，仿真结果变化也较小。从图10可以看出，当制动效能因数从500增加至1 000时，滑移率曲线依然变化很小，也始终保持在0.19～0.20的区间内，再次表明该控制系统具有较高的控制精度和较好的鲁棒稳定性。

图11和图12分别给出了汽车在对接路面上行驶的车速、轮速与制动距离的仿真结果和滑移率变化的曲线。设定在1.5s时刻，汽车由干沥青路面过渡到湿滑路面行驶。从图12可以看出，车轮滑移率并无较大变化，也保持在0.19～0.20的区间内。说明该ABS控制系统对路面条件的变化有很好的鲁棒稳定性。