基于GM(1,1)模型的城镇生活污水排放量预测
2014-02-26杨旭王晓丽
杨旭,王晓丽
(1.郑州大学水利与环境学院,河南 郑州 450001;2.郑州大学力学与工程科学学院,河南 郑州 450001)
随着我国人口的增加、经济的发展和城镇化进程的加快,城镇生活污水的排放呈现逐年增加的趋势,其造成的水体污染已相当严重,成为城镇化进程中不可忽视的问题。为有效地控制污水排放量,减少其对水体的污染,分析和预测未来几年的城镇生活污水排放量十分必要。
1 常用的污水排放量模型
目前常用的污水排放量预测模型和方法为回归分析法、灰色模型、BP人工神经网络法等[1-2]。
回归分析法是一种应用广泛的方法,在污水排放量预测中常用的是多元线性回归,但回归分析要求大样本,只有通过大量的数据才能得到量化的规律,这对很多无法得到或者一时缺乏数据的实际情景的解决带来了困难。
人工神经网络模型是一种包含许多简单的非线性计算单元或连接点的非线性动力系统,而BP人工神经网络是其中应用最广泛的一种。污水排放量与相关影响因素之间关系复杂,BP网络模型强大的非线性映射能力可以较好地处理这方面的问题,然而BP网络模型通常也存在学习效率低、收敛速度慢和易陷于局部极小状态的问题[2]。
灰色系统理论[3]是邓聚龙教授于1982年在国际上首先提出的一种研究“部分信息已知,部分信息未知”的小样本、贫信息的不确定性系统的方法。其中的灰色预测通过对原始数据进行生成处理来寻找系统变动的规律,生成有较强规律性的数据序列,然后建立相应的微分方程模型,从而预测事物未来发展趋势的状况。
灰色预测所需数据量不大,在数据缺乏时十分有效。其不同于回归分析,不建立数据模型,而利用对原始数据进行生成处理后的生成序列数据建立模型,进行预测,不受样本容量的限制,样本不需要规律性分布。其中的GM(1,1)模型是灰色预测中常用的模型。
污水排放量受到人口、经济发展水平、经济结构、居民生活水平、生活习惯等诸多因素的共同影响,影响因素较多且较为复杂,其中有些因素难以清晰的分析与衡量。这些符合灰色系统的特征。现主要运用灰色预测理论,根据2000—2012年全国城镇生活污水排放量的数据(见表1)建立GM(1,1)模型,并对该模型进行精度等级检验。

表1 2000—2012年全国城镇生活污水排放量① 亿t
①数据来自环保部网站的历年《全国环境统计公报》(http://zls.mep.gov.cn/hjtj/qghjtjgb/),其中《全国环境统计公报(2013年)》尚未发布。
2 GM(1,1)模型的建立
灰色预测理论的GM(1,1)建模方法,首先对原始数据序列经过累加生成,后建立微分方程模型,利用微分方程以及初值条件进行数据序列的预测。
设有原始数据序列为:
x(0)=[x(0)(1),x(0)(2),…,x(0)(n)]
(1)
对以上原始数据序列作一次累加生成处理后,得:
x(1)=[x(1)(1),x(1)(2),…,x(1)(n)]
(2)
(3)
式中生成序列式(2)与原始序列式(1)相比较,其平稳程度增加而随机程度得到弱化。生成序列可用一阶微分方程描述其变化趋势。
GM(1,1)的灰微分方程为x(0)(k)+αz(1)(k)=μ
(4)
式中:
z(1)——x(1)的紧邻均值生成序列,称为背景值;
x(0)(k)——灰导数;
α——发展系数;
μ——灰作用量。
对应的白化方程为:
(5)
其初始条件为x(1)(1)=x(0)(1)。式中待定参数α和μ用最小二乘法估计可得:
[α,μ]r=[BrB]-1BrY
(6)
式中B为数据矩阵,Y为参数向量,分别按式(7)和(8)计算,其中:
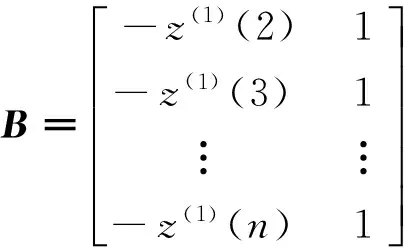
(7)
Y=[x(0)(2),x(0)(3),…,x(0)(n)]r
(8)
求微分方程的解,得到时间响应函数:
(9)
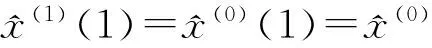
(10)
利用MATLAB编程[4-5]可求得α、μ,由式(10)即可进行数据序列的灰色预测。
3 计算结果

经计算后可以得2000—2012年城镇生活污水排放量的预测值,见表2。
4 模型精度检验与适用性讨论
对建立的GM(1,1)模型按表3进行相对误差、绝对关联度、后验差和小误差概率检验,见表4。
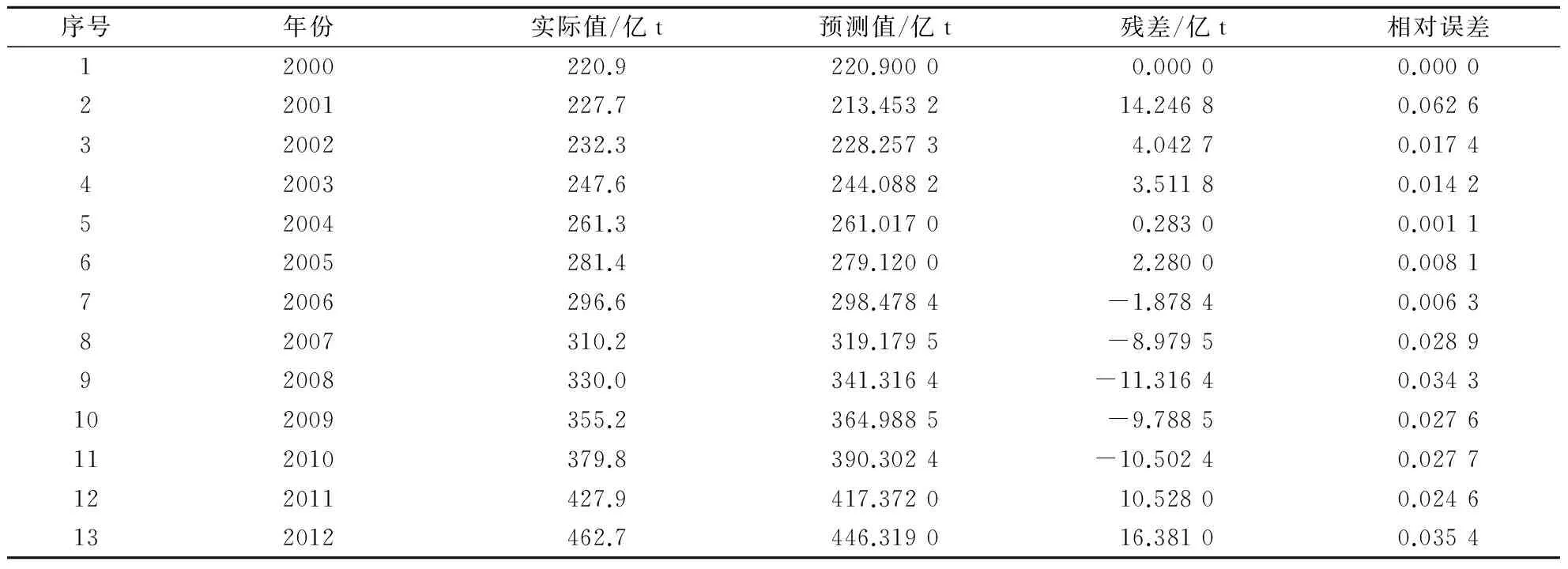
表2 城镇生活污水排放量的GM(1,1)模型计算结果

表3 灰色模型精度检验等级[6]

表4 GM(1,1)模型检验指标值
根据表3与表4的对比可知,相对误差检验结果为二级,绝对关联度、后验差和小误差概率检验结果均为一级,故此模型精度为二级。对比表5的GM(1,1)模型适用范围[7]可知此模型可用于中长期预测。

表5 GM(1,1)模型的适用范围
5 模型预测
用此模型对未来几年城镇生活污水排放量进行预测。2013—2017年全国城镇生活污水排放量预测值见表6。

表6 全国城镇生活污水排放量预测值 亿t
6 结论
(1)2013—2017年全国城镇生活污水的排放量呈逐年上升趋势,从2013年的477.273 6亿t上升到2017年的624.102 2亿t,每年的平均上升速率为29.37亿t。
(2)所选用的灰色预测模型和方法简单易用,不需像回归分析法、BP人工神经网络法那样考虑影响系统行为的种种因素,利用较少的数据即可进行精度较高的预测。但同时应注意,利用GM(1,1)模型所建立的预测函数表达式,反映出其更适用于具有较强指数规律的序列。城镇生活污水排放量较符合这一特征。
[1] 王凤仙,李树平,陶涛.城市污水量预测模型及方法综述[J].河南科学,2009,27(4):483-487.
[2] 王凡.城市污水排放量预测研究[D].上海:华东师范大学,2011.
[3] 邓聚龙.灰色系统理论教程[M].武汉:华中理工大学出版社,1990:1-20.
[4] 唐丽芳,贾冬青,孟庆鹏.用MATLAB实现灰色预测GM(1,1)模型[J].沧州师范专科学校学报,2008,24(2):35-37.
[5] 宋新山,邓伟,张琳.MATLAB在环境科学中的应用[M].北京:化学工业出版社,2008:201-208.
[6] 肖新平,宋中民,李峰.灰技术基础及其应用[M].北京:科学出版社,2005:139.
[7] 刘思峰,邓聚龙.GM(1,1)模型的适用范围[J].系统工程理论与实践,2000,20(5):121-124.
