基于Landsat-8数据和劈窗算法的地表温度反演及城市热岛效应研究
2014-02-26宋挺段峥刘军志严飞黄君吴蔚
宋挺, 段峥, 刘军志,严飞,黄君,吴蔚
(1. 无锡市环境监测中心站,江苏 无锡 214121;2. 代尔夫特理工大学,代尔夫特,2628 CN,荷兰)
0 引言
城市热岛效应是指城市地区整体或局部温度高于周围地区,温度较高的城市地区被温度较低的郊区所包围或部分包围的现象[1]。热量平衡是城市热岛形成的能量基础,城市化改变了城市下垫面的性质和结构,增加了人为热,从而影响了城市热量平衡各分量的变化[2]。城市热岛效应通常被视为一种城市公害,特别是中低纬度地区的夏季,热岛增温效应加剧城市的酷热,致使城市气候舒适度变差,加重了空气污染和资源消耗,影响了城市生态环境质量[1]。
卫星遥感的出现为城市热岛效应的研究提供了新的数据源,其中卫星影像的热红外波段在城市热岛效应研究中应用尤为广泛。已有学者利用热红外波段数据对城市热岛进行了研究,取得了不少成绩[3-6]。目前,在城市热岛遥感研究中,地表温度(Land Surface Temperature, LST)数据主要以遥感图像灰度值、亮度值和遥感反演等方式获取。地物灰度值、亮度温度与地表实际温度相差较大,不能有效支撑城市热岛的定量研究。而基于LST的反演算法则被证明是一种精度较高的地表温度获取方法,适用于城市热岛的定量研究。
在LST反演的众多算法中,劈窗算法是一种精度较高的代表性算法[7-8]。该算法利用10~13 μm大气窗口内两个相邻热红外通道(一般为10.5~11.5 μm和11.5~12.5 μm)对大气吸收作用的不同,通过两个通道测量值的各种组合来剔除大气的影响,进行大气和地表比辐射率的修正。劈窗算法已成为目前由热红外遥感数据获取地表温度的主要方法。
劈窗算法最初主要是针对NOAA/AVHRR(The National Oceanic and Atmospheric Administration/Advanced Very High Resolution Radiometer)与MODIS(Moderate Resolution Imaging Spectroradiometer)等遥感产品而开发,经过20多年的发展,目前公开发表的劈窗算法已将近20个。覃志豪等[9]对12种劈窗算法进行了详细的讨论。劈窗算法的一种表现形式如下:
Ts=A0+A1Ti-A2Tj
(1)
式中:Ts——地表温度;Ti和Tj——热通道i和j的亮度温度;A0,A1和A2——参数,由大气透过率和地表比辐射率等因子确定,不同算法中它们的值各不相同,也可以改写成如下形式:
Ts=Ti+A(Ti-Tj)+B
(2)
式中:Ts,Ti和Tj含义同上;系数A和B也由大气透过率和地表比辐射率等因子确定。
NOAA/AVHRR与MODIS等遥感产品的空间分辨率较低,往往不能满足城市热岛定量研究对精细LST空间分布信息的需求。因此利用劈窗算法和较高分辨率的遥感产品进行LST反演,将有力促进城市热岛的定量研究。2013年2月11号,美国宇航局NASA 成功发射了 Landsat-8 卫星,为走过了40年辉煌岁月的 Landsat系列卫星计划重新注入新鲜血液。Landsat-8上携带有2个主要载荷:陆地成像仪(Operational Land Imager, OLI)和热红外传感器(Thermal Infrared Sensor,TIRS)。Landsat-8数据的2个热红外波段(10和11波段)与MODIS热红外波段的31和32波段的波宽以及中心波长基本一致,具体对比细节如表1所示。

表1 Landsat-8(第10和11波段)与MODIS热波段(31和32波段)数据对比
根据表1中的数据参数,基于劈窗算法和Landsat-8 TIRS数据进行LST反演是可行的。因此,笔者利用Landsat-8的双通道的热红外数据,采用劈窗算法对无锡地区的地表温度进行反演,并根据地表温度对无锡市热岛的空间分布进行分析和研究。
1 数据源与工作流程
1.1 数据源
1.1.1 遥感数据
Landsat-8属于NASA的Landsat系列,属于近极地太阳同步轨道卫星。笔者利用TIRS的10和11波段估算星上亮度温度;利用OLI的3、4、5和6波段生成研究区的归一化植被指数(Normalized Difference Vegetation Index,NDVI)、改进型归一化水体指数(Modified Normalized Difference Water Index ,MNDWI)以及归一化建筑指数(Normalized Difference Barren Index,NDBI)用来参与比辐射率的估算。TIRS与OLI要分别进行辐射定标,笔者还对OLI进行了FLAASH大气校正,各项定标参数可从Landsat-8影像的头文件里获取。
使用2013年12月20日与2014年3月16日包含无锡地区的Landsat-8数据,图幅号分别为LC81190382013344和LC81190382014075。由于缺少夏季的Landsat-8数据参与热岛分析,研究还收集了2013年8月12日的Landsat-7的ETM+数据(图幅号为LE71190382013224),对陆地表面温度反演所使用的方法为单通道算法(SC)[10]。另外,对应时段的MODIS1B数据和MOD11-L2地表温度产品被用于计算水汽含量和对Landsat-8反演的结果进行精度验证。
1.1.2 实测数据
选取无锡市环境监测中心站在无锡太湖水域设立的16个浮标点位(图1)的水温数据作为地面实测数据对反演的LST进行比较和验证。在全部的16个站点,监测频率均为30 min/次。选取了与Landsat-8过境时间最为接近的实测站点数据用于遥感反演结果的验证。

图1 选取的太湖水域内16个实测水温水质自动监测点位分布
1.2 工作流程
首先利用Landsat-8的TIRS数据、OLI数据和MODIS1B数据分别进行亮温、地表比辐射率和大气水汽含量的计算,然后再以上述中间结果作为输入,利用劈窗算法进行LST反演。在反演的地表温度基础上,利用实测水温数据和MODIS温度产品对反演结果进行验证与对比分析,最后用得到的地表温度反演结果进行热岛效应的分级与评价。工作流程如图2所示。
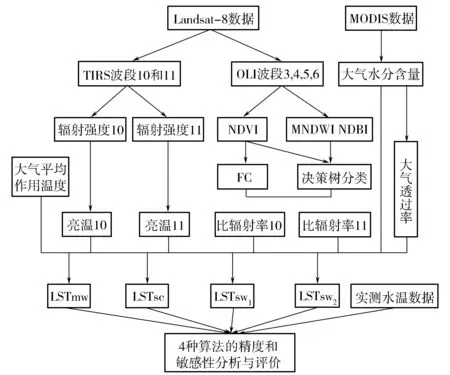
图2 Landsat-8地表温度反演与热岛效应分级评价流程
2 针对Landsat-8影像数据的劈窗算法
2.1 地表热辐射传输方程的构建
地表热辐射传输方程是描述热辐射传播通过介质时与介质发生相互作用(吸收、散射、发射等)而使热辐射能按一定规律传输的方程。遥感器所接受到的热辐射主要有由地表热辐射经大气衰减后被遥感器接受的热辐射(即被测目标本身的热辐射)、大气向上的热辐射(大气直接热辐射)和大气向下热辐射(大气向地面的热辐射)经地表反射后又被大气衰减最终被遥感器接受的热辐射3部分[11-12],故MODIS遥感器所接收到的热辐射计算公式如下:
Bi(Ti)=τi(θ)·[εi·Bi(Ts)+(1-εi)·Li↓]+Li↑
(3)
式中:Ti——Landsat-8通道i的亮度温度;Ts——地表温度;εi——地表比辐射率;τi(θ)——通道i在遥感器视角为θ下从地面到遥感器的大气透射率;Bi(Ti)——遥感器所接收到的辐射强度;Bi(Ts)——在地表温度为Ts时的黑体辐射强度;Li↑和Li↓——大气向上和向下的辐射强度。
此外,由于用大气向上平均辐射强度代替大气向下辐射强度不会产生较大的地表温度误差[9]。
Li↑≈[(1-τi(θ)]·Bi(Ta)
(4a)
Li↓≈[(1-τi(θ)]·Bi(Ta↓)
(4b)
用Ta替代Ta↓对方程的计算不产生实质性的影响,将Li↑与Li↓代入(3)式,简化得到:
Bi(Ti)=εi·τi(θ)·Bi(Ts)+[1-τi(θ)]·[1+(1-εi)·τi(θ)]Bi(Ta)
(5)
式中:Ti和Ts含义同上;Ta——大气向上平均作用温度;εi和τi(θ)含义同上;Bi(Ti)和Bi(Ts)含义同上;Bi(Ta)——通道i的大气向上平均辐射强度。
针对Landsat-8数据的10和11波段,则有:
B10(T10)=ε10·τ10(θ)·B10(Ts)+[1-τ10(θ)]·[1+(1-ε10)·τ10(θ)]B10(Ta)
(6a)
B11(T11)=ε11·τ11(θ)·B11(Ts)+[1-τ11(θ)]·[1+(1-ε11)·τ11(θ)]B11(Ta)
(6b)
式中:B10(T10)、B10(Ts)和B10(Ta)——波段10对应于亮度温度、地表温度和大气向上平均温度的辐射强度;B11(T11)、B11(Ts)和B11(Ta)——波段11对应于亮度温度、地表温度和大气向上平均温度的辐射强度;τ10和τ11——波段10和11的地表比辐射率;τ10(θ)和τ11(θ)——波段10和11从地面到遥感器的大气透过率。
2.2 Planck辐射函数的线性展开
Planck方程是复杂的非线性函数,要想从方程组(6)中直接求出地表温度很难。而用其Taylor展开式的前两项来表示它的近似值,是推导劈窗算法的通用做法[11-13]。依据Planck方程中辐射强度与温度之间的线性关系,通过对Planck方程的泰勒展开并取前两项得到下式:
Bi(Tj)=Bi(T)+(Tj-T)ΔBi(T)/ΔT=(Li+Tj-T)ΔBi(T)/ΔT
(7)
针对Landsat-8波段10或11数据,若上式中i=10或11,j=10或11,则Tj表示波段10或11的亮度温度;若j=s,则Tj表示所要求解的地表温度;若j=a,则Tj表示大气向上平均作用温度;T是任意确定的一个亮度温度;Bi(Tj)和Bi(T)分别是温度为Tj和T时的第i波段的辐射强度。参数Li是辐射强度与其随温度变化率的比值。
针对Landsat-8波段10和11,建立下式的计算Li的表达式:
Li=Bi(T)/[ΔBi(T)/ΔT]
(8)
L10=a10+b10T10
(9a)
L11=a11+b11T11
(9b)
在式(7)中命令T=T10、i=10和j=10,则有:
B10(T10)=(L10+T10-T10)ΔB10(T10)/ΔT=L10B10(T10)/ΔT
(10a)
同理,针对波段10和11其他各个温度,有如下的表达式:
B10(Ts)=(L10+Ts-T10)ΔB10(T10)/ΔT
(10b)
B10(Ta)=(L10+Ta-T10)ΔB10(T10)/ΔT
(10c)
B10(T11)=(L10+T11-T10)ΔB11(T10)/ΔT
(10d)
B10(Ts)=(L10+Ts-T10)ΔB11(T10)/ΔT
(10e)
B10(Ta)=(L10+Ta-T10)ΔB11(T10)/ΔTi
(10f)
2.3 劈窗算法的推导
文中的劈窗算法,是建立在辐射传输方程组(6)的基础上。为了简化起见,将方程组(6)中的系数定义如下:
Ci=εiτi(θ)
(11)
Di=[1-τi(θ)][1+(1-εi)τi(θ)]
(12)
据此,将方程组(6)改写成下式:
B10(T10)=C10B10(Ts)+D10B10(Ta)
(13a)
B11(T11)=C11B11(Ts)+D11B11(Ta)
(13b)
将式(10)代入式(13)中,再将求解Li的式(9)代入,两式相减并消解方程,最终可得到如下的反演地表温度的公式,它就是所要推导的劈窗算法:
Ts=A0+A1T10-A2T11
(14)
式中:Ts、T10、T11含义同上,单位K。A0、A1和A2——系数。表2给出了不同的温度范围时,系数ai和bi的值[14]。可以看出,温度范围减小,精度较高。为了获得准确的地表反演温度,最好是根据温度范围选择系数。

表2 不同温度范围内的TIRS的反演回归系数
最终公式推演如下表示:
A0=a10E1-a11E2
(15a)
A1=1+A+b10E1
(15b)
A2=A+b11E2
(15c)
E1=D11(1-C10-D10)/E0
(15d)
E2=D10(1-C11-D11)/E0
(15e)
A=D10/E0
(15f)
E0=D11C10-D10C11
(15g)
式中:C10、C11、D10和D11可由式(11)和式(12)得出。由式(14)和(15)可知,求解地表温度的关键是确定亮度温度、地表比辐射率、大气透过率和遥感器视角。亮度温度利用Planck方程可直接计算。Landsat-8的TIR最大天顶角仅为7.5°,为窄视场传感器,可以不用考虑天顶观测角的影响。因此下文接着讨论反演地表温度所需的2个参数(大气透射率τ和地表比辐射率ε)的计算。
3 亮度温度、地表比辐射率、大气透过率的计算
3.1 亮度温度
亮度温度是指辐射出与观测物体相等辐射能量的黑体的温度。将影像DN值定标为热辐射强度(Ii)之后,可用Planck函数求解出星上亮度温度,计算公式如下:
Ti=Ki2/ln(1+Ki1/Ii)
(16)

Landsat-8在第10波段的中心波长λ10=10.9 μm;在第11波段的中心波长λ11=12.0 μm,根据Planck公式得出Landsat- 8的Ki1和Ki2常量。
对于第i=10波段,分别为K10 1= 774.89 W/(m2·sr·μm),K10 2=1 321.08 K。
对于第i=11波段,分别为K11 1= 480.89 W/(m2·2sr·μm),K11 2=1 201.14 K。
3.2 地表比辐射率的估计方法
地表比辐射率是物体与黑体在同温度、同波长下的辐射出射度的比值,它受物体的表面状态、介电常数、含水量、温度、物体辐射能的波长、观测角度等多种因素的影响。目前求地表比辐射率的方法主要有差值法、独立温度光谱指数法(TISI)和NDVI门槛值(NDVITHM)等方法[15-16]。
对于Landsat系列影像图像,地表比辐射率主要取决于地表的物质结构和遥感的波段区间。地球表面不同区域的地表结构虽然很复杂,但从卫星像元的尺度来看,可以大体视作由4种类型构成:水面、建筑、裸土和植被[17]。水面结构简单;建筑包括城市和农庄,主要由道路、各种建筑和房屋组成;植被包括林地和农田等。
3.2.1 典型地物的比辐射率
水体在热波段范围内的比辐射率很高,接近于黑体。植被的比辐射率也很高,一般认为在0.981~0.983。HUMES等[18]测量结果表明,全覆盖灌木叶冠的热波段辐射比率为0.986左右。典型土壤的平均比辐射率为0.972 15左右。对于城镇的各种建筑表面而言,在11.5~12.5 μm波段范围内,其比辐射率一般在0.960~0.980之间变动,取其中值,比辐射率大约在0.970左右,略小于自然土壤的地表比辐射率。
根据如上判定,确定landsat-8的10与11通道比辐射率值如下:εi w、εi v、εi s和εm分别是水体、植被、裸土和建筑在第i(i同上)波段的地表比辐射率。分别取ε10w=0.996 83,ε11w=0.992 54,ε10v=0.986 72,ε11v=0.989 90,ε10s=0.967 67,ε11s=0.977 90,ε10m=0.964 885,ε11m=0.975 115。
3.2.1.1 自然表面比辐射率的估计方法
实际上,组成自然表面的象元可以简单看作是由不同比例的植被叶冠和裸土组成,即混合象元。对于面积较大的100%植被或裸土表面,可直接用这两种类型的地表比辐射率来表示象元的比辐射率,因此,当Pv=1时,ε=εv;当Pv=0时,ε=εs。但是,通常很难有100%的植被覆盖或裸土表面,因此,覃志豪等[17]通过下式来估计混合象元的地表比辐射率。
εi=PvRvεiv+(1-Pv)Rsεis+dε
(17)
式中,Pv——植被覆盖度,即植被的构成比例:Pv=(NDVI-NDVIs)/(NDVIv-NDVIs),其中NDVIv与NDVIs分别为植被和裸土的NDVI值,文中取NDVI的5%置信区间来定义。Rv和Rs——植被和裸土的温度比率。在地表相对平整的情况下,一般可取dε=0;在地表高低相差较大的情况下,dε可以根据植被的构成比例简单估计。由于热辐射相互作用在植被与裸土各占一半时达到最大,所以,覃志豪等[17]提出如下经验公式来估计dε:
当Pv<0.5时,dε=0.003 8Pv
当Pv>0.5时,dε=0.003 8(1-Pv)
当Pv=0.5时,dε最大,dε=0.001 9
值得指出的是,用公式算出的ε如果大于εv,则取ε=εv。
3.2.1.2 城镇地表比辐射率的估计方法
城镇在地表温度反演中也很重要,尤其是在村庄较密集的地区或城市郊区。一般来说,城镇像元的地表比辐射率与确定自然表面比辐射率的方法类似。由于城镇主要是由各种建筑表面和分布其中的绿化植被所组成,因此有:
εi=PvRvεiv+(1-Pv)Rmεim+dε
(18)
式中:Rm——建筑表面的温度比率;εim——建筑表面的比辐射率。
3.2.1.3 典型地物温度比率估计
比较准确的地表比辐射率估计需要对典型地物的温度比率进行估计。为了确定典型地物的温度比率,根据主要地表类型的温度差异进行模拟,得出Ri随植被覆盖度变化而变化的状况。覃志豪等[17]提出用如下公式估计植被、裸土和建筑表面的温度比率:
Rv=0.933 2+0.058 5Pv
(19a)
Rs=0.990 2+0.106 8Pv
(19b)
Rm=0.988 6+0.128 7P
(19c)
这一估计虽然没有考虑温度变化的影响,但基本上已经能够满足地表温度反演对地表比辐射率估计的要求。
3.2.2 地表构成比例的确定
文中使用分类回归决策树(Classification And Regression Tree,CART)对地表进行分类,决策树模型分类法结构明确,能自动选取特征并融入影像以外的各种知识,是人工智能遥感信息的主要提取方法之一,广泛用于地表分类的研究中。
结合地物光谱特征和光谱影像信息,建立分类规则,将地表分为植被、建筑物、裸土和水体4个部分。文中使用NDVI、MNDWI与NDBI 3种遥感信息指数对地表信息进行决策树分类。
根据NDVI指数、MNDWI指数和NDBI指数结合人工判定阈值构建无锡地区地表分类的决策树模型。以2014年3月16日为例,根据10%置信度,NDVI阈值取0.65,MNDWI取0.17,NDBI取-0.05,构建模型流程如图3所示。

图3 决策树模型分类流程
分类后,对水体、植被、裸土、建筑物分别计算其地表比辐射率。其中,10波段水体的比辐射率ε10w=0.996 83,11波段水体的比辐射率ε11w=0.992 54;植被和裸土等自然表面的比辐射率根据公式(14)得出;建筑物的比辐射率根据公式(15)得出。
3.3 大气透过率的计算
在地表反演过程中,水汽是估计大气透过率的主要考虑因素。通常的做法是通过MODTRAN、6S和LOWTRAN等大气模型软件模拟大气透过率与水汽含量的关系[19]。因为实时的大气剖面资料很难获得,所以这种模拟结果精度有时难以保证。
覃志豪等[20]提出了求算透过率的方法,即通过MODTRAN来计算大气水汽含量和透过率的关系,然后通过大气水汽含量来求算透过率。对于Landsat-8数据而言,大气水汽含量很难从影像反演得到,文中使用与Landsat-8影像同一天的MODIS数据,根据毛克彪[21]的方法,可以用MODIS第2和第19波段来反演大气水分含量,推算公式如下:
ω={[α-ln(ρ19/ρ2)]/β}2
(20)
式中:ω——大气水汽含量,g/cm2;α和β——常量,α= 0.02,β=0.632 1;ρ19和ρ2——MODIS第19和2波段的地面反射率。
大气透过率与大气水汽含量的关系主要通过大气模拟来确定。根据中纬度大气剖面数据进行模拟[22],得出大气透过率估算方程:
τ31=2.897 98-1.883 66e-(ω/-21.227 04),R2=0.997 48
(21a)
τ32=-3.592 89+4.604 14e-(ω/-32.706 39),R2=0.996 85
(21b)
由于Landsat-8第10和11通道的中心波长与MODIS第31和32通道的中心波长基本相对应,所以式(21)推得的31通道与32通道的大气透过率,基本适用于Landsat-8的第10和11通道的大气透过率。
4 无锡市地表温度反演结果分析
4.1 温度反演的比较验证
可根据实测值或其他标准值对一个反演算法进行对比验证,文中利用无锡市环境监测站在太湖水域建立的水质自动监测站的实测水温数据进行比对,并结合美国宇航局提供的MODIS地表温度数据集进行相对验证。
文中选取16个太湖水域的水质自动监测站的水温数据,监测数据的时间精度可以达到30 min,完全可以满足对遥感数据进行比对的数据同步的要求。
同时MOD11-L2级MODIS温度产品也被用于验证基于Landsat-8反演的LST结果的精度。该MODIS产品根据WAN等[23]提出的多通道反演计算,能同时反演地表温度和比辐射率。在晴朗天气条件下,MODIS温度产品误差在1K以下[24]。该MODIS温度产品过境时间为当地时间11:35,Landsat-8卫星过境对应的当地时间为10:33,两者差距接近1 h,MODIS过境时间的实际地表温度应稍高于Landsat-8过境时间的实际地表温度。得到的水温比对的结果如表3所示(其中,Landsat-8统计数据为空间分辨率100 m的象元,MODIS地温产品空间分辨率为1 000 m)。

表3 基于Landsat-8反演得出的LST、MODIS地温产品与实测数据比对结果 K
从表3可以看出,2014年3月16日Landsat- 8反演的对照点的平均水温是284.93 K,MODIS温度产品的平均水温是286.09 K,而实测的平均水温为284.96 K。从平均值来看,Landsat-8反演的水温比MODIS温度产品较实测的误差更小,仅为0.03 K,而MODIS温度产品较实测误差有1.13 K。从绝对误差来看,Landsat-8反演的水温的平均绝对误差为0.52 K,较MODIS温度产品的1.13 K也明显要小。2013年12月20日的结果也类似, Landsat-8反演的水温较实测水温的平均绝对误差为 0.62 K,较MODIS温度产品的1.29 K也明显要小。
由于Landsat-8热红外数据空间分辨率是100 m,而MODIS地表温度产品空间分辨率是1 km,所以Landsat-8热红外数据需重采样到1 km,以便与MODIS数据保持一致。重采样为1 km分辨率的Landsat-8反演结果和MODIS温度产品的影像对比见图4。

图4 2014年3月16日Landsat-8地温反演结果与MODIS地温产品对比
文中采用最小值、最大值和平均值这些统计指标对反演结果进行评价。分别对Landsat-8地表反演结果与MODIS地温产品设置0.5%的置信区间,以去除异常值。统计结果如表4所示。

表4 2014年3月16日Landsat-8劈窗算法反演结果与MODIS地温产品对比统计 K
由于不可避免地存在一定几何校正方面的误差,统计区域范围会有略微的偏差。从无锡区域的统计来看,利用劈窗算法对Landsat-8温度数据反演值相对于MODIS地温产品最小值误差为-1.2 K,最大值误差为2.7 K,平均值误差为-0.1 K。虽然平均值误差很小,但是由于MODIS的温度产品过境时间为11:35,Landsat-8卫星过境时间为10:33,两者差距接近1 h,在这段时差里,温度变化大概为1K左右,且水域温度上文已做过比较,MODIS温度产品的水温比Landsat-8反演的水温要高1 K左右。所以两者陆地区域的实际平均误差应该在1K左右,利用劈窗算法对Landsat-8陆地温度数据反演值要略高于MODIS地温产品,而水域温度数据较MODIS温度产品更接近于实测值,表明该方法具有一定的可信精度。
还需要指出的是,Landsat-8的2013年12月10日的数据,无锡区域基本无云,数据质量较高,无锡区域反演的平均温度为284.4 K。但是MODIS比Landsat-8晚过境1 h,在MODIS过境的时候,无锡陆地区域上空已经有了薄云层,造成MODIS地温数据较实际要低,与Landsat- 8反演数据相比,平均值要低2.3 K,再考虑到MODIS比Landsat-8晚过境1 h,且水温数据比Landsat-8反演水温又要略高,陆地表面温度的实际差别可能要达到3 K以上,综合MODIS产品陆域上空薄云层的影响与统计结果差异较大的原因,这一天MODIS地温产品陆地表面温度数据不建议用作比对。
4.2 敏感性分析
敏感性分析通常是先假定某一参数有一微小误差,其他参量不变或者在指定的范围内变化,分析不同情况下由这一误差带来的最终结果的变化。通过下式可以分析参数误差引起反演地表温度的误差[25-26]:
式中:△Ts——地表温度的反演误差;△x——参数x的估计误差;Ts(x+△x)和Ts (x)——用(x+△x)和x进行反演得到的地表温度。
文中以2014年3月16日的Landsat-8数据为例,进行敏感性分析。
4.2.1 比辐射率敏感性分析
首先对比辐射率的影响进行分析,结果表明:给定温度,大气越干燥,比辐射率影响越大;一定的大气状况,温度越高,影响反演结果越大;同样的比辐射率误差,通道的波长越长,所引起的温度误差越大。
通过对地表比辐射率不同改变值的设定,同时其他参量不变,进行地表比辐射率的敏感性分析。将2014年3月16日第10与11波段的比辐射率都增加与减去一定的量,值分别为0.01,0.02,0.04和0.06。最终得到的结果如表5所示。

表5 地表比辐射率变化时,地表温度反演结果
从表5可以看出,随着比辐射率的降低,反演得到的LST基本是等量升高的,但升高的幅度略微增加。地表比辐射率每改变0.01,反演得到的LST改变0.66 K,劈窗算法对地表比辐射的敏感性较低。
4.2.2 水汽含量敏感性分析
由于大气透过率是基于大气中的水汽含量,预计大气透过率的偏差会在波段10与波段11都会发生。因此,敏感性分析是对水汽含量作为模型的自变量。
通过对水汽含量不同浓度的设定,同时其他参量不变,进行水汽含量的敏感性分析。
将水汽含量设为0.5,1,1.5,2,2.5,3,4,5和6 g/cm2,对2014年3月16日的数据分别代入进行计算,最终得到的结果如表6和图5所示。

表6 水汽含量为变化时,地表温度反演结果

图5 水汽含量变化时候反演LST趋势
由表6和图5可以看出:劈窗算法反演得到的地表温度结果呈一元多次函数上升,在低水汽含量(ω<1 g/cm2)情况下,对水汽的敏感性较高,在中等水汽含量(1 g/cm2<ω<3 g/cm2)的情况下, 敏感性较低,在高水汽含量(ω>3 g/cm2)情况下,敏感性又略微升高,总体来说,敏感性不是很高,水汽含量每变化1 g/cm2,劈窗算法的地表温度反演结果平均变化0.4 K左右。
由于地物的比辐射率误差较小,一般在1%以内,而水汽含量使用MODIS的实时数据进行反演,误差也不会很大,从而表明该算法具有较高的精度,可满足大多数研究和应用需求。
5 城市热岛效应与分析
在反演LST的基础上,计算城市热场变异指数以定量分析城市热岛效应[27]。某点的LST与研究区域平均LST的差值同研究区域平均LST之比,可用于描述该点的热场变异情况:
HI(T)=(T-TMEAN)/TMEAN
(22)
式中:HI(T)——热场变异指数;T——城市某点的遥感反演LST;TMEAN——城市研究区域的平均LST。
为了更直观地描述城市热场变化情况。进一步采用阈值法将热场变异指数分为6级[25]。该指标的阈值划分以及对应的生态意义见表7。

表7 热岛效应评价指标的阈值划分
以上文中反演的无锡及其周边区域的LST为基础,计算该地区的城市热场变异指数,并且按照生态评价指标的阈值进行分级,分别制作出2013年12月10日、2014年3月16日和2013年8月12日,分别代表冬季、春季和夏季的分级图(图6)。
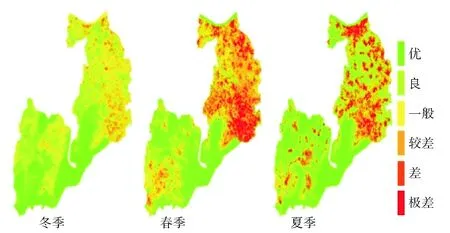
图6 冬季、春季与夏季无锡市热岛效应生态评价分级
表8为热岛效应等级面积比例与对应的LST平均值。
无锡市地表温度在不同的季节变化较大,具体表现为:冬季(12月)地表最高温度为290.4 K,最低地表温度为278.9 K,平均温度为284.7 K;春季(3月)地表最高温度为304.2 K,最低地表温度为283.4 K,平均温度为294.7 K;夏季(8月)地表最高温度为324.9 K,最低地表温度为292.5 K,平均温度为312.3 K,季节变化明显。

表8 热岛效应等级面积比例与对应的LST平均值
从热岛效应等级面积比例来看,冬季相对高温区所占面积比例较少,强和极强所占面积比例仅为2.52%;春季与夏季相对高温区所占面积比例相近,强和极强所占比例分别为18.07%和17.31%。冬季相对低温区面积比例最高,无与弱所占比例为66.52%;夏季次之,无与弱所占比例为62.56%;春季相对低温区面积比例最高,无与弱所占比例为47.18%。
从热岛效应强度来看,冬季热岛效应等级为无时,LST的平均温度为282.15 K,热岛效应等级为极强时,LST的平均温度为291.74 K,差异 9.56 K;春季热岛效应热岛效应等级为无时,LST的平均温度为289.73 K,热岛效应等级为极强时,LST的平均温度为302.35 K,差异为12.62 K;冬季热岛效应等级为无时,LST的平均温度为306.32 K,热岛效应等级为极强时,LST的平均温度为2 323.52 K,差异为17.2 K。夏季的热岛效应强度最强,春季次之,冬季最弱。
利用之前完成的土地利用分类结果,结合地面温度反演结果,得到不同地表覆盖类型的LST平均值,如表9所示。

表9 各地表覆盖类型对应的LST平均值 K
从表9可以看出,不同地表覆被类型的LST相差较大,城镇和裸土表面温度相对较高,植被和水体温度相对较低。在春夏季,不同地表覆盖类型之间的地表温度差异尤其明显。这是由于地表性质的差异对地表能量交换有重要影响。在同样的太阳辐射条件下,水体因反射率高且比热较大,升温慢,植被因蒸腾作用吸收热量降温,所以这两类区域平均LST较低,对热岛起到缓解作用。而城镇区和裸土反射率低且比热较小,因此LST明显高于其他地表覆盖类型。基于上述分析,可以通过合理规划城市建筑密集度以及增加城市绿化带和水域面积,来改善城市热岛效应。
6 结语
文中基于Landsat-8的光学和热红外数据,采用劈窗算法反演了地表温度LST,并采用同步的MODIS温度产品和地面实测的16个站点水温数据进行了比较和验证。结果表明,基于Landsat-8数据的劈窗算法误差<1 K,比MODIS 温度产品更为接近地面实测的水温数据。文中进一步对劈窗算法涉及的关键输入参数(大气水汽含量和地表比辐射率)进行了敏感性分析。结果表明,在正常的大气水汽含量和地表比辐射率变化的情况下,其误差较低(1 K左右)。因此,利用Landsat-8进行劈窗算法反演地表温度,具备较高的精度,可满足大多数研究应用需求。
在LST反演结果的基础上,计算了可直观反映城市热岛效应的HI指数,发现无锡市春夏季热岛效应较冬季更为明显。不同的地表覆盖类型对热岛效应的贡献不同,植被和水体因具有明显的降温作用,对热岛起到了缓解作用。
笔者在基于劈窗算法和Landsat-8数据的LST反演方面取得了初步结论,但仅使用了一种劈窗算法进行反演计算。为进一步提高地表温度反演的精度,在今后的工作中,将基于Landsat-8数据采用多种反演方法进行比对分析,以更好地辅助城市热岛效应的定量研究。
[1] 叶柯,覃志豪.基于MODIS数据的南京市夏季城市热岛分析[J].遥感技术与应用,2006(5):426-431.
[2] 杨士弘.城市生态环境学[M].北京:科学出版社,2002.
[3] 刘文渊,谢亚楠,万智龙,等.不同地表参数变化的上海市热岛效应时空分析[J].遥感技术与应用,2012(5):797-803.
[4] 刘玉安,唐志勇,程涛,等.基于HJ-1B数据的武汉市LST反演及热环境分析[J].长江流域资源与环境,2014(4):526-533.
[5] 吴传庆,王桥,王文杰,等.利用TM影像监测和评价大亚湾温排水热污染[J].中国环境监测,2006(6):80-84.
[6] 白杨,孟浩,王敏,等.上海市城市热岛景观格局演变特征研究[J].环境科学与技术,2013(3):196-201.
[7] GAO C X,TANG B H,WU H,et al. A Generalized Split-Window Algorithm for Land Surface Temperature Estimation from MSG-2/SEVIRI Data[J].International Journal of Remote Sensing,2013,34(12): 4182-4199.
[8] LI Z L, TANG B H,WU H,et al.Satellite-derived land surface temperature: Current status and perspectives[J]. Remote Sensing of Environment,2013,131:14-37.
[9] 覃志豪,ZHANG M H, ARNON K. 用NOAA-AVHRR热通道数据演算地表温度的劈窗算法[J].国土资源遥感,2001(2):33-42.
[10] JUAN C J,SOBRINO J A,NINYEROLA M,et al.Revision of the single-channel algorithm for land surface temperature retrieval from Landsat thermal-infrared data[J].IEEE Trans.Geosci.Remote Sens,2009,47(1):339-349.
[11] COLL C,CASSELLES V,SOBRINO A. On the Atmospheric Dependence of the Spit-window Equation for Land Surface Temperature[J].International Journal of Remote Sensing,1994(15):1105-1112.
[12] 柳钦火,徐希孺.遥测地表温度与比辐射率的迭代反演方法[J].遥感学报,1998,2(1):1-9.
[13] FRANCA G B,GRACKNELL A P.Retrieval of Land and Sea Surface Temperature Using NOAA-11 AVHRR Data in Northeastern Brazil[J].International Journal of Remote Sensing,1994(15):1695-1712.
[14] OFFER R,QIN Z H,YEVGENY D,et al.Derivation of Land Surface Temperature for landsat-8 TIRS Using a Split Window Algorithm[J].Sensors,2014(14):5768-5780.
[15] 刘玉洁,杨忠东.MODIS遥感信息信息处理原理与方法[M].北京:科学出版社,2001.
[16] 俞宏,石汉青.利用分裂窗算法反演陆地表面温度的研究进展[J].气象科学,2002,22(4):494-500.
[17] 覃志豪,李文娟,徐斌,等.陆地卫星TM6波段范围内地表比辐射率的估计[J].国土资源遥感,2004(3):28-32.
[18] HUMES K S,KUSTAS W P,MORAN M S.Variability of emissivity and surface temperature over a sparsely vegetated surface[J].Water Resources Research,1994,30:1299-1310.
[19] 毛克彪,覃志豪, 施建成,等.针对MODIS影像的劈窗算法研究[J].武汉大学学报:信息科学版,2005(8):703-707.
[20] 覃志豪,LI W J,ZHANG M H.单窗算法的大气参数估计方法[J].国土资源遥感,2004(5):37-43.
[21] 毛克彪.用于MODIS数据的地表温度反演方法研究[D].南京:南京大学,2004.
[22] MAO K,QIN Z,SHI J.A practical split-window alogorithm. for retrirving L and surface temperature from MODIS data[J].Intemational Joumal of Remote Sensing,2005,15(26):3181-3204.
[23] WAN Z M,LI Z L.A Physics-Based Algorithm for Retrieving Land-Surface Emissivity and Temperature From EOS/MODIS Data[J].IEEE Transaction on Geoscience and Remote Sensing,1997,35(2):980-996.
[24] WAN Z M,ZHANG Y L,ZHANG Q C.Quality Assessment and Validation of the MODIS Global Land Surface Temperature[J].International Journal of Remote Sensing,2004,25(1):261-274.
[25] 高懋芳,覃志豪,刘三超.MODIS数据反演地表温度的参数敏感性分析[J].遥感信息,2005(6):3-6.
[26] QIN Z H,DALL O G.Derivation of spit window algorithm and its sensitivity analysis for retrieving land surface temperature from NOAA-advanced very high resolution radiometer data[J].Geophys Research, 2001,106(D19):22655-22670.
[27] 张勇,余涛,顾行发. CBERS-02 IMRSS热红外数据地表温度反演及其在城市热岛效应定量分析中的应用[J].遥感学报,2006,10(5):789-797.
