马特拉算法在遥测数据短期预测中的应用
2014-02-26任国恒
任国恒,朱 变,朱 海
(周口师范学院计算机科学与技术学院,河南 周口 466001)
0 引 言
遥测数据直接反映了卫星在轨运行的状态.卫星的遥测数据具有非平稳变化的特点,而具有非平稳性的遥测数据的各阶常用统计量(如均值、自相关函数等)经常随时间的变化而改变[1],这给遥测数据的预测带来了很大的困难.传统的预测方法,如自回归模型(Auto-Regressive model,简称AR)、自动回归移动平均模型(Auto-Regressive and Moving Average model,简称ARMA)等常用预测模型,适合处理平稳的数据[2],对于非平稳的数据不能满足预测需要.
笔者通过对卫星历史遥测数据分析研究建立适用于非平稳时间序列的预测模型,对遥测参数的未来趋势进行短期预测,通过预测遥测数据序列潜在的故障趋势,为指导故障发生前的正确决策提供重要支持[3],降低卫星潜在的风险,提高卫星运行可靠性.
笔者以卫星运行期间太阳翼的输出功率数据为研究对象.太阳翼的输出功率序列具有随机性和一定的周期性,这是不同频率分量的叠加结果.遥测数据的不同频率分量可分两部分,即慢变和快变,其中慢变部分反映了序列主体,快变部分体现了序列的细节[4].对遥测数据进行短期的预测要求能够捕捉到在时域上表现瞬时、随机的分量.由于遥测数据的趋势中心随时间变化,传统的时域分析方法不能准确分析瞬时、随机的分量变化规律,而小波分析可对遥测数据信号中的频率分量进行粗细分离.
1 小波变换相关工作
采用多分辨率分析思想用小波变换对遥测数据序列进行分解,得到反映序列主体变化的低频分量和代表序列细节的高频部分[5].遥测数据原始序列根据所选择的小波基函数和适宜的分解尺度被分解为频率不同的分量,各分量在长度上与原序列保持一致[6].低频分量代表原始序列中基本不变的主体部分[7],即太阳翼基本输出功率;高频分量表示原序列中的瞬时、随机的分量,即太阳翼随机输出功率.
1.1 小波基选择
在工程应用中小波函数除了要满足容许条件和正则性条件,还要满足以下3个条件:良好的紧支撑性;Ψ(t)具有消失矩;满足正交性.常用的小波函数,如Morlet、Mexican小波函数不存在尺度函数,即不满足正交性;Haar小波在时域上不是连续的,不适合做小波基.笔者选择dbN(Daubechies小波)小波函数做小波基,dbN小波是具有高阶消失矩的紧支集正交小波函数,阶数N的具体取值通过小波变换对实际序列分解的结果判定.
图1是某同步卫星太阳翼输出功率序列采用dbN小波在N取1、2、3时进行分解后,近似部分与原序列的比较结果.N为3时,较好的体现了序列的变化趋势,且趋势中的突出点被保留下来;N为1、2时,序列的平滑度不利于分量预测模型的建立.所以,选择db3小波作为小波基对原序列进行分解.

图1 dbN小波分解结果Fig.1 Decomposition result based on dbN
1.2 分解尺度研究
遥测数据的变化是缓变和快变结合,与之对应的是长度周期嵌套.这是时间序列的能量集中分布在一些频率带上的结果[8].因此,将不同的频率分量分开,使其变化规律更加直观.
对遥测序列进行分解结果是将原序列分解为几个细节部分和一个近似部分.分解尺度偏大,序列的采样密度会变稀,序列的主体曲线会越来越平滑,导致获得的近似序列失真;分解尺度若偏小,序列的主体变化趋势又不太明显,不易观察到各分量的变化规律[9].
图2是经db3小波分解后的近似部分aN在不同尺度下的分解结果.分析图2发现分解尺度

图2 不同分解尺度下近似部分比较Fig.2 Comparation of aN with different scale
为2时,近似部分的曲线a2已经足够光滑,同时保持了原曲线的形状;而a3、a4随着分解次数的增加,采样点减少,所得曲线过分平滑,序列的变化趋势已失真,因此本文选择的分解尺度为2.
2 基于小波变换的预测模型构建
2.1 周期自回归模型
若有一时间序列X,表达式为
Xt=a0t+a1tXt-1+…+aptXt-p+εt
(1)
满足以下条件:


XKT+T=a0T+a1TXKT+T-1+…+
apTXKT+T-p+εKT+T
(2)

a01+a11Xn+…+ap1Xn-p-1
(3)

(4)
对于遥测数据分解序列建立一小时预测模型,选取周期的长度为60,即p=T=60.负荷序列的PAR模型如式(5):
(5)
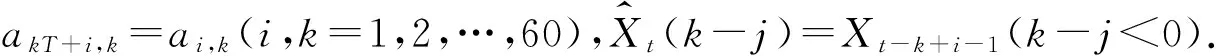
遥测数据短期预测模型共有未知参数(p+1)T个,记为
a(i)=(a0,i,a1,i,…,a60,i)
(6)
式(5)中的未知参数可由式(6)确定.已知ai拟合式(5)的残差平方和定义为
St=
[Xn+k-a0,kXt(k-1)-…-a60,kXt(k-60)]2
(7)


j=0,1,2,…,p
(8)
2.2 遥测数据短期预测模型
利用马特拉(Mallat)小波变换算法和db3小波基对太阳翼输出功率数据序列进行2尺度的分解,图3是对4小时内的输出功率负荷的原始序列和进行分解后的小波分量结果.
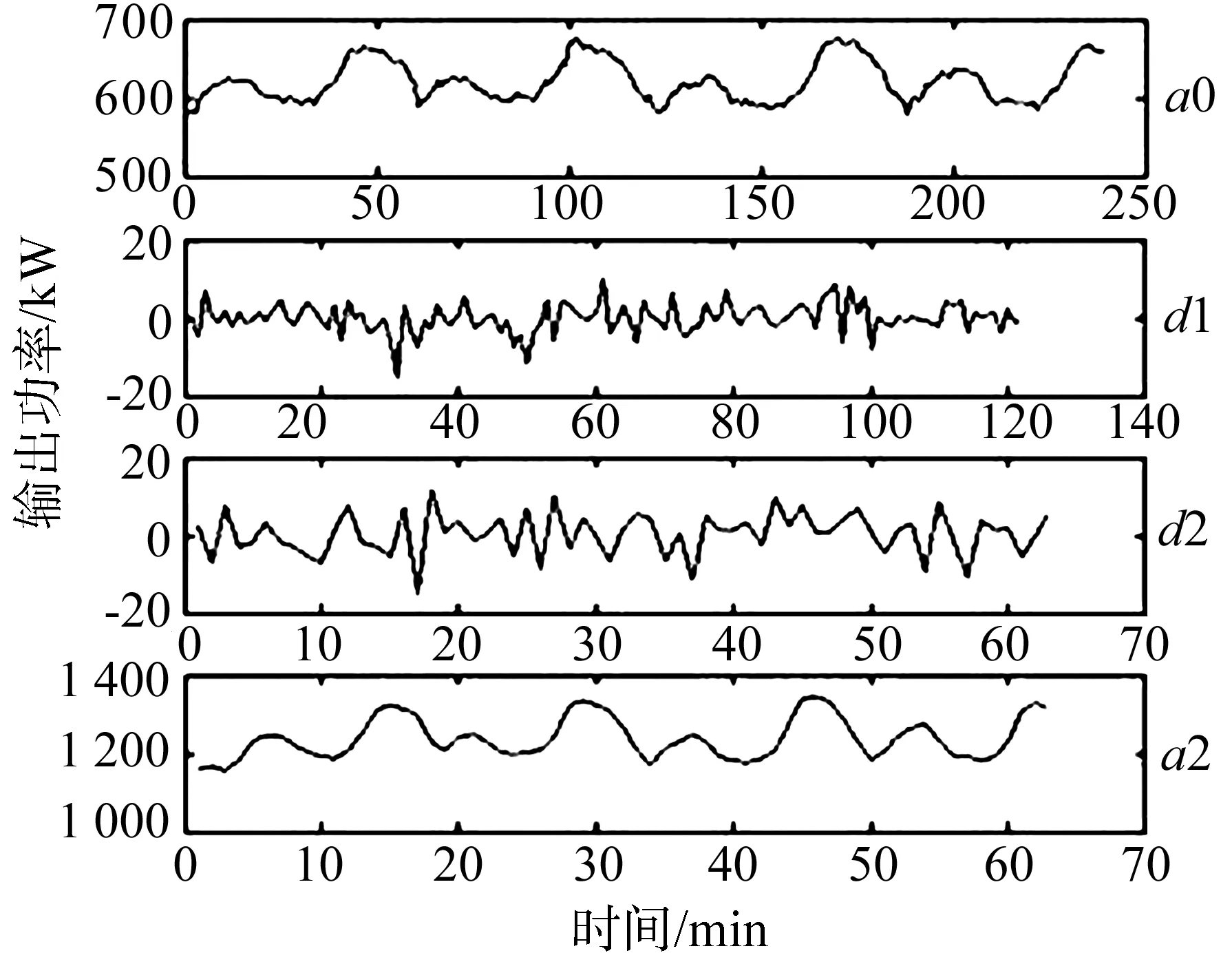
图3 太阳翼输出功率数据分解结果Fig.3 Decomposition result of solar panel output power
从图3可以看出对数据进行2尺度分解后,得到的低频数据a2具有较强的周期性,这是因为低频数据反映原序列的主体信息,变化规律较强;高频数据d1、d2体现原序列的细节,是待分解序列中变化较快的部分.
由于分量d1、d2和a2的曲线变化特征不同,应根据不同分量的特点构建预测模型.笔者对各个子序列作如下区别对待:
(1)主体信息a2周期性显著,变化相对平缓,对分解得到的15个点进行周期自回归预测;
(2)高频分量d1、d2随机性较强,为提高预测的实时性,高频部分采用二次指数平滑法进行预测.
指数平滑法由R.G.Brown提出,该算法的优点是预测模型构建过程中只需少量的历史数据,计算量小,便于实时预测.模型建立过程中是利用算法对原始时间序列的不规则性进行平滑,获得原序列的变化规律和趋势,对未来某时刻的数据进行预测,更多的考虑数据的更新.指数平滑法计算公式如式(9):
Yt=yt=axt -1+(1-a)yt -1
(9)
式(9)中:xt -1、yt -1分别是t-1时刻的实际值和预测值;yt为t时刻的平滑值;Yt为t时刻的预测值;a为平滑系数,取值范围为0 Yt=yt= axt+(1-a)[yt -1+(yt -1-yt -2)] (10) 式(10)中:xt为t时刻的实际值;yt为t时刻的二次指数平滑预测值;yt -1、yt -2为t-1时刻的一次指数平滑值;一次指数平滑与二次指数平滑区别是二次指数平滑利用一次指数平滑得到的预测值来建立预测模型.二次指数平滑的预测模型为: (11) 指数平滑法对高频数据预测时平滑系数a根据时间序列的情况在0~1之间选择.由图3可以看出高频数据的变化的随机性很大,笔者在实际计算中将a的取值范围定在了0.6~0.8,对平滑参数a取不同值时高频序列d1、d2进行预测后的均方根误差分析发现,序列d1、d2在a=0.8时,均方根误差最小,因此,笔者在进行实际计算中取平滑参数a值为0.8. 针对太阳翼输出功率所建立的基于Mallat算法的时间序列预测模型框图如图4所示. 图4 基于Mallat算法的预测模型框图Fig.4 Forecasting model based on Mallat algorithm 基于构建的模型对所研究某卫星2011年1月12日11:00至15:00这4小时太阳翼输出功率为历史数据输入模型,对未来15:00至16:00这1小时内输出功率进行预测.图5为低频数据a2和高频数据d1、d2的预测结果. 图5 低频数据a2和高频数据d1、d2的预测结果Fig.5 Prediction result of a2 and d1、d2 对各分量序列进行重构的预测值与原始输出功率趋势进行对比的结果如图6所示. 图6 基于Mallat算法的预测值Fig.6 Forecasting value based on Mallat algorithm 通过实际的太阳翼输出功率的变化趋势与预测值的对比分析发现预测结果的边界和突变的趋势不是很理想. Mallat算法对序列进行分解时,每分解一次都要进行二元抽样,使得序列不能在每个时间点上建立直观的尺度关系,影响了对突变点的预测.另外,小波变换算法都是建立在多分辨分析的基础上的,在快速Mallat算法中每次进行小波变换时都把序列看成是无限长的,但是在实际的应用中,输出功率序列是有限的.所以,待预测序列在经Mallat小波变换算法分解时会对序列进行延拓,这就使得在对各个子序列进行重构时,小波变换后的低频部分和高频部分的数据总数将大于原始输入序列的长度;并且这种情况在滤波器长度增大时,数据量也会随之增大,显然会引起边界数据不可信,在重构预测结果时导致峰值和谷值的预测误差也较大.通过上面的分析可知,预测误差是由以下3种原因产生的: (1)用Mallat进行序列分解时因抽样产生的误差; (2)输入的序列长度有限,而经小波变换算法后使各个子序列的长度增加,并将此数据作为了各个序列预测的初始值; (3)各子序列的预测结果进行重构时,在进行小波逆变换时并没进行数据的压缩,没有实现精确的重构从而产生预测误差. Mallat算法自身产生的误差无法消除,针对后两种情况的解决方案是在对序列进行分解前,先对序列的边界进行延拓.在小波分析中常用的边界延拓方法有零延拓、周期延拓、平滑延拓等.由于太阳翼输出功率本身就有一定的周期性,所以笔者选用周期延拓对序列进行边界的延拓,周期延拓的思想是将信号看成是一个周期信号. 具体的处理工作如下: (1)对序列进行小波变换前先对序列进行边界延拓,使其成为无限长的序列,让序列通过滤波器并进行隔点抽样,保证尽可能不丢失信息的情况下,对各个子序列适当的截取低频部分和高频部分,以保证序列的数据总量不变; (2) 在重构前先对有限的子序列延拓,然后进行向上的抽样并滤波,对滤波后的结果进行适当的截取,恢复原信号. 图7 修正后的预测值Fig.7 Corrected forecasting value 由图7可以看出,在对序列进行延拓后再做小波变换,所得的预测结果要比直接做小波变换所得预测结果的边界吻合效果更加理想. 对笔者提出的预测模型和常用的指数平滑模型的性能进行分析评价.以平均绝对误差、均方值误差、计算时间、最大误差为评价的指标,分别对未来1小时的输出功率进行预测.经计算,基于Mallat算法的预测时间为25.76 s,平均绝对误差为1.545,最大误差为5.196,均方根误差为1.891;指数平滑模型的预测时间为18.76 s,平均绝对误差为1.418,最大误差为5.996,均方根误差为2.040.由此可见,笔者提出的预测模型在预测精度上具有明显的优势,预测时间相对增加的原因是原始序列需要经过频率分解,增加了计算量,但在卫星遥测数据的短期预测应用中,预测的精度是预测模型性能的主要评价指标. 笔者依据卫星遥测数据短期预测的要求和意义,对遥测数据特性进行了分析,针对遥测数据具有非平稳性和一定周期性的特点,笔者提出了基于Mallat算法对遥测数据序列进行分解的方法,将序列中的分量分解到不同的频率带上,非平稳序列简化为变化缓慢的平稳序列和一些特殊的序列的分量组合.针对每个分量的变化特点建立合适的时间序列预测模型对各个子序列进行预报,并将各个子序列的预测结果采用小波变换的逆算法进行重构,依据模型,以历史输出功率数据为源数据对未来1小时的输出功率进行预测,并进行验证分析,得到理想的预测结果,表明笔者提出的预测方法可以有效的解决遥测数据的短期预测问题,满足了工程应用需要. 致 谢 本研究在开展、实验验证分析过程中和论文撰写过程中,西安工业大学于帆教授提出了很多宝贵的建议,谨致谢意.感谢国家自然科学基金委员会对本研究提供的资金支持. [1] 郭小红,徐小辉,赵树强,等.基于新信息灰色预测的卫星遥测数据参数状态预测及应用[J].宇航学报,2010(8):1938-1943. GUO Xiao-hong,XU Xiao-hui,ZHAO Shu-qiang,et al.Satellite telemetry parameter trend forecast algorithm based on new information and application[J].Journal of Astronautics,2010(8):1938-1943.(in Chinese) [2] 孙振明,姜兴渭,王晓锋,等.Trous小波在卫星遥测数据递归预测中的应用[J].南京理工大学学报,2004,28 (6):606-611. SUN Zhen-ming,JIANG Xing-wei,WANG Xiao-feng,et al.Application of Trous wavelet to satellite telemetry data recursive prediction[J].Journal of Nanjing University of Science and Technology,2004,28 (6):606-611.(in Chinese) [3] 余国浩,蔡远文.自适应指数平滑法预测遥测数据实时趋势研究[J].装备指挥技术学院学报,2007,18(2):66-69. YU Guo-hao,CAI Yuan-wen.Research on exponent-smoothing model with variable parameters applied in real-time trend prediction of telemetry data[J].Journal of the Academy of Equipment Command &Tchnology,2007,18(2):66-69.(in Chinese) [4] 鲁明.卫星数据的信息识别[D].哈尔滨:哈尔滨工业大学,2006. LU Ming.Recognition of information from satellite data [D].Harbin:Harbin Institute of Technology,2006.(in Chinese) [5] 刘辉,田红旗,陈超,等.基于小波分析法与神经网络法的非平稳风速信号短期预测优化算法[J].中南大学学报:自然科学版,2011,42(9):2705-2709. LIU Hui,TIAN Hong-qi,CHEN Chao,et al.Short-term forecasting optimization algorithm for unsteady wind speed signal based on wavelet analysis method and neutral networks method[J].Journal of Central of South University:Science and Technology,2011,42(9):2705-2709.(in Chinese) [6] TAI Nengling,Jurgen Stenzel,WU Hong-xiao.Tech-niques of applying wavelet transform into combined model for short-term load forecasting [J].Electric Power Systems Research,2006,76(6/7):525-533. [7] 徐军华.电力系统短期负荷预测模型与优选的研究[D].成都:四川大学,2004. XU Jun-hua.Research on power system short-term load forecasting model and optimum selsction[D].Chengdu:Sichuan University,2004. [8] TANG Jian,LUAN Jiahui,LIU Yalong,et al.A novel design of prediction interval for telemetry data [C]// Proceedings of the Annual Reliability and maintainability symposium (RAMS),24-27 January 2011,Lake Buena Vista,FL2011:1-5. [9] LIU Yu,ZENG De-liang,LIU Ji-zhen,et al.Short-term wind speed forecast based on wavelet packet transform and LS-SVM[C]//Proceedings of the 2012 24th Chinese Control and Decision Conference(CCDC),23-25 May 2012,Taiyuan,China.Sigapore:IEEE Industrial Electronics(IE)Chapter2012:2811-2814.
3 遥测数据预测实例分析

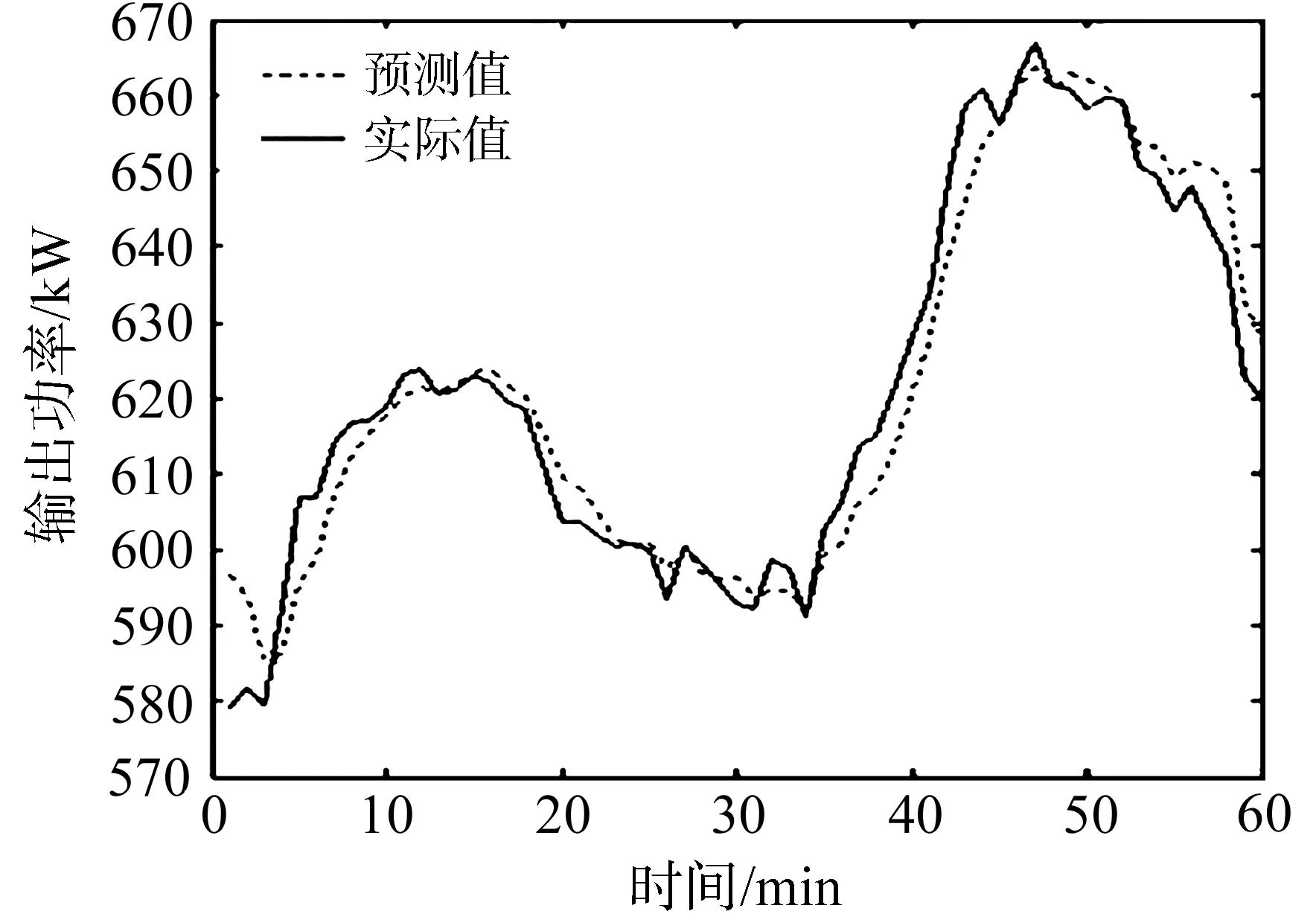


4 结 语
