格莱圈密封性能非线性有限元分析
2014-02-26王成刚盖超会
王成刚,肖 健,刘 慧,刘 俊,高 兴,盖超会
(1.武汉工程大学机电工程学院,湖北 武汉430205;2.武汉软件工程职业学院机械制造工程系,湖北 武汉430205)
0 引 言
近年来,随着尖端科学技术的迅速发展和工业、交通运输等部门机械化、自动化水平的不断提高,对密封件的性能和质量要求也就愈来愈高[1].本文所研究的对象是缸阀一体化气缸,此气缸是清洁煤气化装置机械振打除灰系统的关键设备,由于工况的复杂性,现有的冲击气缸使用寿命短,可靠性差等已越来越不能满足工业生产的需求.缸阀一体化气缸的重要部件是密封件.所以衡量气缸正常工作的重要指标,就是密封件的使用年限以及其工作的可靠性.
Glyd(格莱圈)密封圈包括方型圈以及O型圈两个部分,通常方型圈材料为含金属粒子的聚四氟乙烯,具有耐磨、耐热等.在运动过程中,方型圈与运动的部分相接触.安装时,方型圈与O型圈通过径向组合安装在同一个密封沟槽中,通过在O型圈上施加一定的压缩量,使O型圈产生较大的变形而回弹,从而达到使气体无法从O型圈和方型圈之间以及O型圈与沟槽之间流通的目的,同时通过O型圈的回弹力传递到方型圈与缸壁之间的接触表面,从而防止了气体从方型圈与缸壁接触表面流通.随着气体压力增加,气压把方型圈以及O型圈推向沟槽的一侧,使得方型圈和O型圈与密封沟槽壁面产生紧密的接触,O型圈因此发生大变形,并进一步挤压方型圈,使方型圈与缸壁接触面之间的接触压力进一步增加.随着气压的增加,接触压力同时增加.
Glyd密封圈中不仅利用了O型圈自紧式密封的特性,更利用了方型圈与缸壁表面接触低摩擦的特点,使得Glyd密封圈具有许多优势,聚四氟乙烯与金属的摩擦系数是所有固体中最低,静摩擦和动摩擦几乎完全相等,因此其摩擦磨损小,使用寿命长[2].此种密封形式相对于普遍的O型圈最大的优势在于增加了耐磨的方形圈,而且也兼顾了O型圈的回弹性.目前国内大多数学者对密封元件的有限元研究一般都集中在最简单的密封件(橡胶O形圈),对组合密封结构的研究极少.故这对以后的密封的分析具有很大意义.
1 Glyd密封圈弹性体的本构模型
1.1 弹性体的物理非线性
对于橡胶超弹性体不可压缩的特性[3-4].为了得到它一般性质精确的表达式,应借助唯象处理方法,这在国内外有许多描述方法,而最常见的就是应变能函数.应变能函数可表示为:
式中:Sij为Piola-kirchhoff应力;W为应变能函数;Eij为Green应变张量.
本文采用基于应变不变量表示应变能密度函数的Mooney-Rivlin本构模型用于分析超弹性材料[5-8].其应变能密度函数模型如下:
式中:Cij为Mooney模型常数,由材料实验所确定;对于不可压缩材料J=1.
其简化后的应变能函数,常见的有二参数、三参数、五参数以及九参Mooney-Rivlin模型,但本文采用二参数数Mooney-Rivlin模型描述,其函数描述如下:
W=C10(I1-3)+C01(I2-3)
式中:W为应变能密度,J/m3;C10、C01为材料的Mooney-Rivlin系数;I1、I2为第一第二张量不变量,J/m3.
本文采用此简化的应变函数模型,穆尼常数分别取为C10=1.87和C01=0.47[9].
1.2 弹性体的几何非线性
Glyd密封圈是由O型圈和方型圈组合而成.O型圈是一种超弹性体,在实际工作过程中,O型圈被挤压后产生回弹力,经由方型圈将压力传递给密封接触面,Glyd密封圈因此而达到密封目的.橡胶材料的分析已经远远超过了线性理论的范畴.
2 Glyd密封圈有限元分析
2.1 Glyd密封圈有限元模型建立
由于该整体结构具有对称性,故只取一个截面来作分析对象,以便简化且真实地反应实际几何结构和受力状态,图1为简化的Glyd密封圈实体模型.丁腈橡胶O形圈和聚四氟乙烯滑环采用二维实体单元PLANE182;不锈钢缸筒、密封槽采用4节点二维实体单元PLANE42,图2为Glyd密封圈有限元模型.

图1 Glyd密封圈实体模型Fig.1 Solid model of Glyd Seal

图2 Glyd密封圈有限元模型Fig.2 Finite element of Glyd Seal
各种材料的性能参数如表1所示.
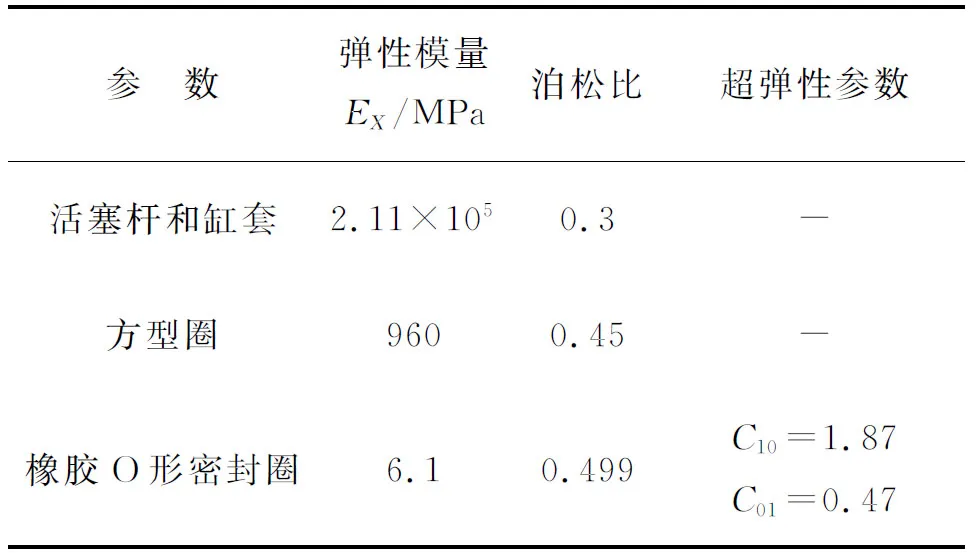
表1 各种材料参数表Table 1 Material parameter
2.2 Glyd密封圈接触分析
Glyd密封圈分析的边界条件非常复杂,其中包含了接触计算,此为弹性体的边界非线性.而接触问题是一种高度的非线性行为,由于在整个分析中,接触状态在改变,故对整个的分析造成很大的困难.
方型圈与O型圈的接触问题是非线性行为.对于它们之间的接触问题必须满足无穿透约束条件.因此必须建立一种关系防止接触表面相互穿过.在当今力学理论、计算数学以及计算机技术的发展基础上,各国学者提出了很多关于接触问题的有限元算法,其中最具有代表性的有拉格朗日乘子法、罚单元法以及直接约束法[10-11].
本文在运用ANSYS软件分析接触问题时,则采用罚单元法进行描述.从变分角度看,罚单元法可以用下式表示.
π=W+We+Q
式中:π为结构总势能;W为应变势能;We为外力势能;Q为接触力势能.
接触面不被穿透的问题可以采用以上表达式解决.建立的接触单元如图3所示,模型中含有多个接触对,接触类型为“面面接触”,其中接触单元和目标单元分别为CONTA172和TARGET169.

图3 接触单元示意图Fig.3 Schematic diagram of the contact unit
3 计算结果及分析
Glyd密封圈主要是依靠O型圈受挤压后变形产生的回弹力,挤压方型圈与不锈钢缸套相接触,形成较大的接触压力,从而达到密封流体的效果,采用Glyd密封圈主要是为了防止流体压力过大导致将O型圈挤入间隙之中从而将O型圈破坏,如此将达不到密封的效果,故加入方型圈能有效的防止此类情况发生.
3.1 “安装”状态下的模型约束
在实际情况中,Glyd密封圈安装在活塞杆密封槽中,再由缸套加上一定的配合挤压方型圈进而使O型圈产生变形,从而达到密封的效果.因此在ANSYS分析中,可以简化为,给定密封槽全约束,给定缸套一定的Y向位移,使Glyd密封圈达到“安装”的状态,之后再给定一定的气体压力,模拟在实际情况中,密封结构的实际变化.
图4(a)~(d)就是Glyd密封圈在压缩率分别为8%、10%、12%、14%时所受到的位移分布图.

图4 “安装”状态下的位移云图Fig.4 Displacement nephogram of installation condition
3.2 密封面间最大接触压力
密封面的最大接触压力是衡量密封结构的密封性能的重要指标,只有接触压力大于流体压力时,密封件才能有效的防止密封介质泄露.
3.2.1 气压对接触压力的影响 图5为在相同压缩率,不同流体压力的情况下,Glyd密封圈的接触压力及变形云图.这里仅仅引用了在实际压缩率(8%)的情况下的接触压力及变形云图.
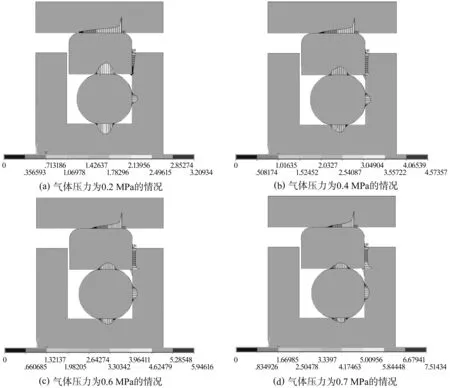
图5 8%压缩率条件下接触压力及变形云图Fig.5 Contact pressure and deformation nephogram under the conditions of 8% compression ratio
从图5中可以看出,方型圈与缸套之间的接触压力和方型圈与O型圈的接触压力都明显高于气体的压力,且验证了在通入气体之后,方型圈和O型圈没有挤入间隙之中,从而很好的保护了Glyd密封圈,故在实际工况中,Glyd密封圈能达到良好的密封效果.从以上的图中可以比较得出最大的接触压力与流体压力之间的关系图,如图6所示.
从图6中可以看出,在不同压缩率的情况下,密封面的最大接触压力随着气压的增加而增加,且与流体的压力成正比,从而验证了弹性体在密封的结构中起到的自紧作用.当通入不同气压的时候,密封面的最大接触压力始终大于通入气压,故此密封件能满足密封的要求.
3.2.2 压缩率对接触压力的影响 图7为在相同压力,不同压缩率的情况下,Glyd密封圈的接触压力及变形云图.这里仅仅引用了在实际工作压力(0.4 MPa)的情况下的接触压力及变形云图.

图6 最大接触压力与气体压力关系图Fig.6 Diagram of the maximum contact pressure and gas pressure
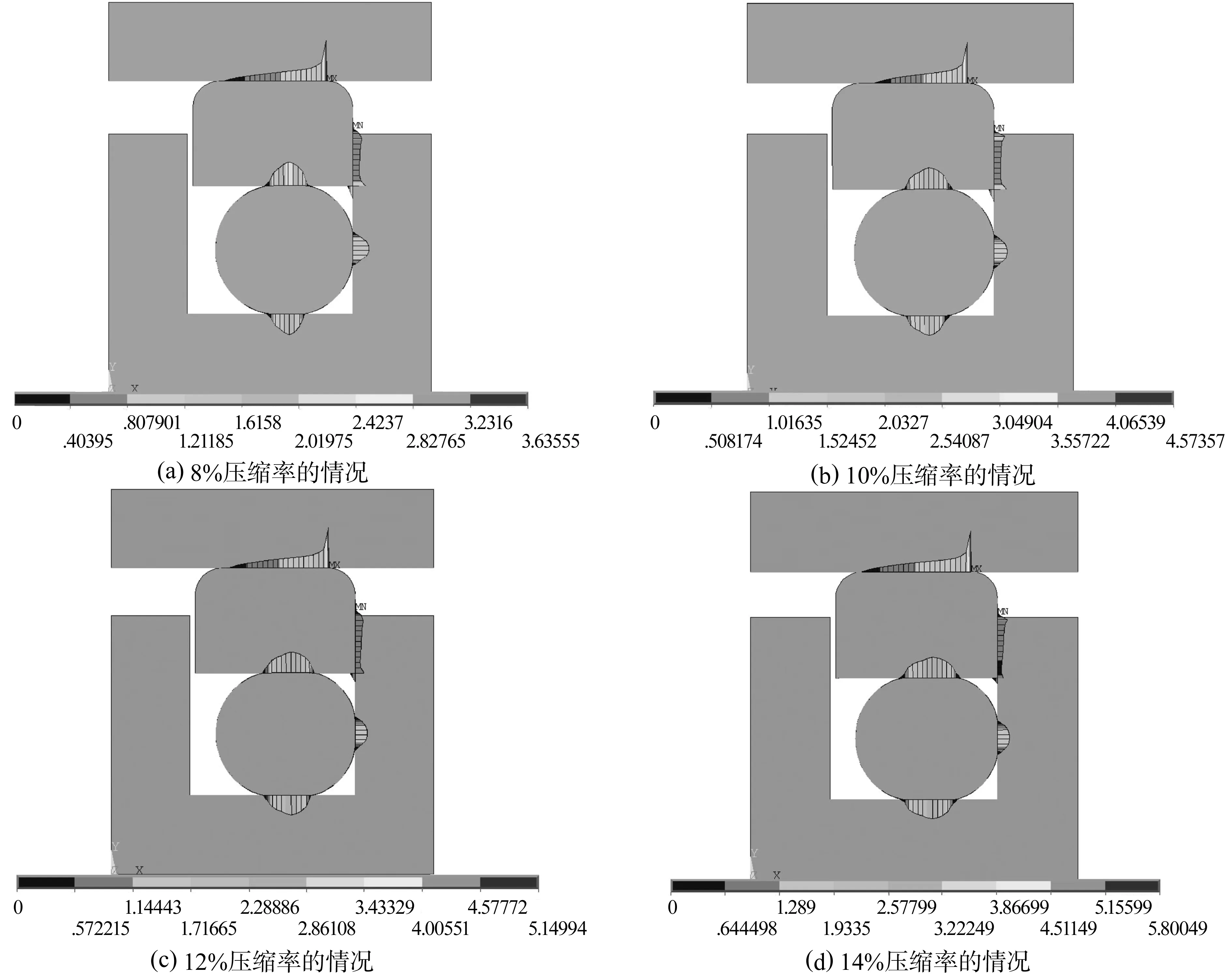
图7 0.4 MPa工作压力下接触压力及变形云图Fig.7 Contact pressure and deformation nephogram under 0.4MPa working pressure
从图7可以看出接触压力随着压缩率的增加而增加,因此压缩率可以选择的尽量大一些;但是压缩率也不宜过大,当压缩率过大时,将会增加接触面的接触压力,从而使得接触面的摩擦阻力变大,产生摩擦热,这样会使得方型圈发热老化,进而失效.因此应控制好安装时的压缩率[12].
从图7中可以比较得出最大的接触压力与压缩率之间的关系图,其关系图如8所示.

图8 最大接触压力与压缩率关系图Fig.8 Diagram of the maximum contact pressure and compression ratio
从图8可以看出,在不同压缩率的情况下,随着压缩率的不断增加,密封结构处的最大接触压力也在增加,而且与压缩率成正比,从而验证了弹性体在密封结构中起到的自紧作用.在对比不同压缩率情况下密封面的最大接触压力时,发现其压力始终大于气体的压力,故此密封件能满足密封的要求.
4 结 语
(1)在预紧压缩率的情况下,最容易出现失效的地方为Glyd密封圈的方型圈与缸套接触的地方,此处的接触压力最大.而此方型圈的材料是耐磨材质,能很好的提高其使用寿命.
(2)施加气压后,在一定的压缩率的情况下,Glyd密封圈向气压低的一方挤压,方型圈与密封槽接触的地方接触压力很小,此接触力大于气体压力.能保证不泄漏,且组合圈也不会被被挤压到间隙中,这样避免了沟槽对O型圈的剪切,很好的提高了密封的性能.
(3)Glyd密封圈密封面的最大接触压力随着气压和压缩率的增加而增加.在气压一定时,适当的增加压缩率能提高密封圈的密封性能;但同时必须得保证密封圈的良好性能.故密封圈的压缩率须控制在一定的范围之内.
致 谢
感谢国家自然科学基金委员会、武汉工程大学科学研究基金对本研究工作的支持和资助,同时感谢周宁波对本文在理论上做出的提示.
[1] 贺庆平,张付英,沈晓斌.基于有限元分析的液压往复密封优化设计[J].机械设计与制造,2008(7):6-8. HE Qing-ping,ZHANG Fu-ying,SHEN Xiao-bin.Optimization of sealing o- ring based on finite element analysis[J].Machinery Design & Manufacture,2008(7):6-8.(in Chinese)
[2] 严桃平,赵迎生.新型组合密封圈的密封机理及其应用[J].机床与液压,2003(1):244-245. YAN Tao-ping,ZHAO Ying-sheng.Sealing principle of new type combined seal and its application[J].Hydromechatronics Engineering,2003(1):244-245.(in Chinese)
[3] 喻九阳,高九阳,王成刚,等.机械振打器活塞杆处0形圈不同密封结构下的性能分析[J].润滑与密封,2010,35(3):65-68. YU Jiu-yang,GAO Jiu-yang,WANG Cheng-gang,et al.Analysis of sealing performance of O-ring with different structure for piston rod of rapping device[J].Lubrication Engineering,2010,35(3):65-68.(in Chinese)
[4] 陈以文,喻九阳,谢洪波,等.自动振打除灰装置活塞处双向密封研究[J].武汉工程大学学报,2011,33(10):77-80. CHEN Yi-wen,YU Jiu-yang,XIE Hong-bo,et al.Comparative analysis and selection for sealing slructure between piston and rod of rapping dewice[J].Journal of Wuhan Institul of Technology,2011,33(10):77-80.(in Chinese)
[5] 李振涛,孙鑫晖.O形密封圈密封性能非线性有限元数值模拟[J].润滑与密封,2011,36(9):86-90. LI Zhen-tao,SUN Xin-hui.Finite element numerical simulation of the sealing performance of O-ring seals[J].Lubrication Engineering,2011,36(9):86-90.(in Chinese)
[6] Fired I,Johonson A R.Nonlinear computation of axisymmetric solid rubber deformation[J].Computer Methods in Applied Mechanics and Engineering,1998(67):241-253.
[7] Nikas G K.Elastohydrodynamics and mechanics of rectangular elastomeric seals for reciprocating piston rods[J].ASME J.Tribol.,2003(125):60-69.
[8] Nikas G K,Sayles.Nonlinear elasticity of rectangular elastomeric seals and its effect on elastohydrodynamic numerical analysis[J].Tribol.Int.2004,37:651-660.
[9] 高九阳,喻九阳,王成刚,等.沟槽对O形圈密封结构性能的影响[J].武汉工程大学学报,2010,32(7):78-80. GAO Jiu-yang,YU diu-yang,WANG Cheng-gang et al.Effects of grooves on sealing performance of O-ring seal structure [J].J. Wuhan Inst.Tech,2010,32(7):78-80.(in Chinese)
[10] 周恩涛,李建勋,林君哲.液压缸活塞密封性能的有限元分析[J].润滑与密封,2006,176(4):84-89. ZHOU En-tao,LI Jian-xun,LIN Jun-zhe.Fin ite element analysis of piston seals property of hydraulic cylinders[J].Lubrication Engineering,2006,176(4):84-89.(in Chinese)
[11] 张婧,金圭.O形密封圈接触压力的有限元分析[J].润滑与密封,2010,35(2):80-83. ZHANG Jing,JIN Gui.Finite element analysis of contact pressure on O-ring[J].Lubrication Engineering,2010,35(2):80-83.(in Chinese)
[12] 谭晶,杨卫民.O形橡胶密封圈密封性能的有限元分析[J].润滑与密封,2006,181(9):65-69. TAN Jing,YANG Wei-min.Finite element analysis of the sealing performance of O-ring seal structure[J].Lubrication Engineering,2006,181(9):65-69.(in Chinese)
