单层厚壁圆筒爆破压力的分布规律与参数

袁小会，刘 岑，吴元祥，刘 兵，刘小宁,*

(1.武汉软件工程职业学院机械工程学院，湖北 武汉 430205；2.武汉工程大学机电工程学院，湖北 武汉 430205)

0 引 言

单层厚壁圆筒是超高压容器的主要类型，也是人造水晶、粉末冶金、低密度聚乙烯生产中的关键设备.目前，工程上把单层厚壁圆筒的爆破压力视为确定量，采用福贝尔(Faupel)公式计算并确定圆筒的壁厚[1-2].

文献[2]指出福贝尔公式的计算误差为±15%左右；文献[3]对提高公式精度进行了有益探索，按组合与置换现有公式的方法，建立了6个新公式.

圆筒制造材料的屈服与抗拉应力、圆筒的几何尺寸等因素存在随机不确定性[4]，考虑这些因素的随机不确定性，探索得到精度高的公式，是建立压力容器可靠性设计方法必须研究的课题，分析厚壁圆筒爆破压力分布规律与分布参数是其中的一项基础工作[5-9].

文中以福贝尔公式与有代表性的3个新公式[3]为研究对象，基于单层厚壁圆筒爆破压力的30组试验数据，应用似然分析理论与方法[5,10]，对厚壁圆筒爆破压力的分布规律与参数分布区间进行研究，解决了建立厚壁圆筒可靠性设计方法的一个基础问题.

1 基础理论

1.1 爆破压力计算公式

计算厚壁圆筒爆破压力的福贝尔公式为

(1)

式(1)中，K为径比(圆筒外直径与内直径之比)；γ为圆筒材料屈强比，γ=σs/σb；σs、σb分别为圆筒材料的屈服与抗拉强度，MPa.

三个计算厚壁圆筒爆破压力的新公式为[3]

(2)

(3)

(4)

1.2 爆破压力的分布规律与分布参数

为分析爆破压力的分布规律与参数，以及研究公式的精度，定义如下具有统计性质的随机变量.

(5)

式(5)中，ri为式中i的随机变量；Pb为爆破压力的实测值，MPa；ubi为爆破压力式中i的理论值，MPa.

对于每个试验数据，根据式(1)～(4)，可得到:

(6)

式(6)中，Pbj为第j个圆筒爆破压力的实测值，MPa；ubi,j为式(i)计算第j个圆筒爆破压力的理论值，MPa；ri,j为式中i对第j个数据的统计值；m为试验数据个数.

对m个试验数据进行统计，可得到ri的准确度、精密度及变异系数

(7)

(8)

(9)

如果把爆破压力的理论值ubi作为确定量，根据式(5)可知，爆破压力Pb与ri分布规律相同，但是两者的分布参数不同.

1.2.1 分布规律的假设检验 对随机变量ri分布规律进行假设检验的具体方法是[5,10]：

①假设ri基本符合正态分布.

③对于符合正态分布的随机变量ri，其统计量ri,j落在分组区间[ai,t，ai,t+1]内的理论概率为：

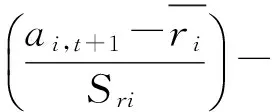
(10)

式(10)中，ai,1=(ri,j)min，ai,M+1=(ri,j)max，其中(ri,j)min、(ri,j)max分别为ri,j中的最小与最大值.

④计算每个分组区间实际频数(Ni,t)与理论频数(m·pi,t)差异的皮尔逊统计量之和，即计算：

(11)

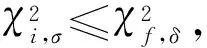
1.2.2 分布参数的取值区间 如果ri基本符合正态分布，在双侧置信度为(1-α)时，ri的均值、标准差与变异系数的分布区间为[10]

(12)

(13)

(14)

上标l与u分别表示分布参数在一定置信度下的较小值与较大值.

工程上一般取δ=0.05与α=0.02，文中所用的t分布系数与χ2系数如表1所示[10].

表1 t与χ2系数Table 1 Coefficient of t and χ2

由于Pb与ri分布规律相同，根据式(5)与式(12)～(14)可知，在双侧置信度为(1-α)时，Pb的均值μPb、标准差与变异系数的分布区间为

(15)

(16)

(17)

式(15)～(17)中，μPb、σPb、CPb分别为Pb的均值、标准差与变异系数.

2 爆破压力的分布规律与分布参数

2.1 爆破压力的分布规律

如果不考虑端部效应对厚壁圆筒爆破压力的加强作用，文献[2，11-13]提供了径比范围为1.33～4.71，圆筒材料屈强比范围为0.402 7～0.885 2的30个爆破压力试验数据；圆筒材料抗拉应力、屈强比与数据来源如表2所示.对式(1)～(4)精度的计算结果如表3所示.

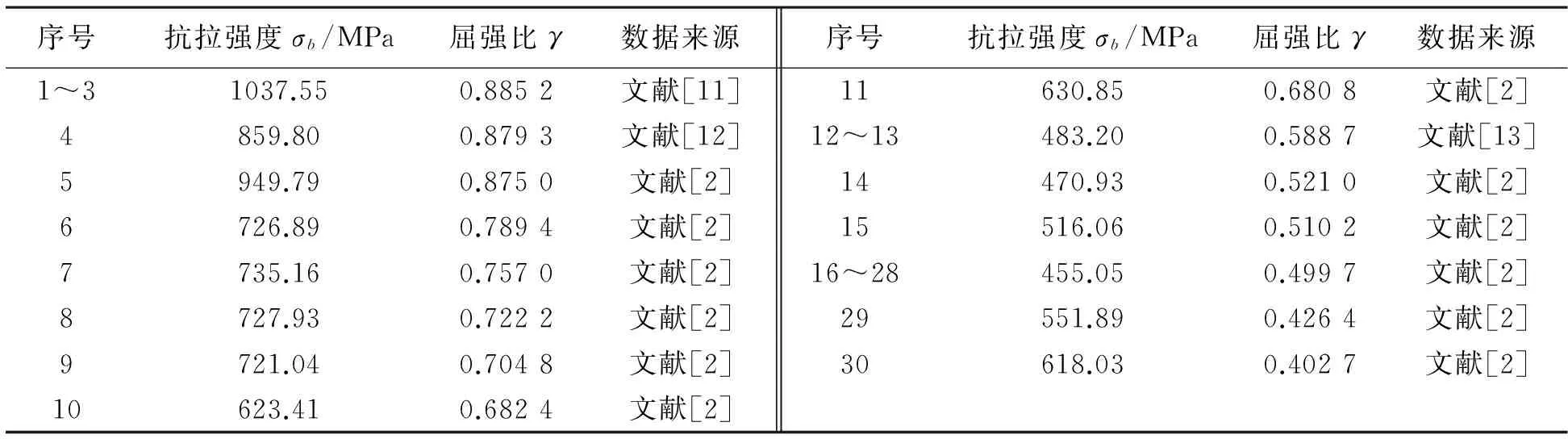
表2 试验容器数据Table 2 Data of test vessel

表3 四个公式的统计计算Table 3 Statistical calculation of four formulas

表4 爆破压力分布规律的统计数据(基于30个试验数据)Table 4 Statistics of burst pressure distribution law(based on 30 test data)

2.2 爆破压力分布参数的取值区间

由于超高压厚壁圆筒制造材料屈强比较大[2]，因此，可把表2中序号为1～28的28个试验数据进行统计分析，其数据一并列入表3；此时容器材料屈强比范围为0.499 7 ～ 0.885 2，径比范围为1.33～4.71.

在双侧置信度为98%时，把表1、表3中的数据代入式(12)～(14)，得到r1～r4的均值、标准差与变异系数范围，如表5所示.

当用式(1)～(4)计算厚壁圆筒爆破压力时，Pb基本符合正态分布，把表5数据代入式(15)～(17)，在双侧置信度为98%时，可得到厚壁圆筒爆破压力Pb分布参数的取值区间，如表6所示.

表5 r1，r2，r3与r4分布参数的取值区间(双侧置信度为98%)Table 5 Distribution parameter intervals value of r1,r2,r3 and r4(bilateral confidence of 98%)

表6 爆破压力分布参数的取值区间(双侧置信度为98%)Table 6 Distribution parameter intervals value of burst pressure(bilateral confidence of 98%)

3 爆破压力计算公式的精度比较

3.1 精度指标

设计公式的精度是指公式的计算值与试验数据(真值)之间的接近程度，可采用差值法或者比值法研究公式精度，均值与变异系数是分析设计公式精度的重要指标[14].

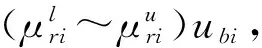
②爆破压力Pb的变异系数.Pb的变异系数Cri是反映Pb稳定性最重要的参数，此值越小，表明Pb变异程度小，公式的精度越高.

3.2 公式精度比较

①由表6及以上分析可知，当K=1.33～4.71时，如果把式(1)～(4)的应用范围从γ=0.402 7～0.885 2改变为γ= 0.499 7～ 0.885 2，公式(1)～(4)的精度分别有所提高.因此，适度改变应用范围，可提高公式精度.

②由表5、表6及以上分析可知，当式(1)～(4)的应用范围为γ=0.402 7～0.885 2与K=1.33～4.71时，均值的精度依次由式(1)(4)(2)(3)从高到低，变异系数的精度依次由式(2)(3)(1)(4)从高到低；当式(1)～(4)的应用范围缩小为γ= 0.499 7～0.885 2与K= 1.33～4.71时，均值的精度依次由式(1)(4)(3)(2)从高到低，变异系数的精度依次由式(2)(3)(4)(1)从高到低.因此，在应用范围相同时，公式(1)～(4)的精度指标互有优劣，似存在精度比福贝尔公式(1)高的公式.

4 结 语

1)考虑容器制造材料的屈服与抗拉应力、容器的几何尺寸等因素存在的随机不确定性，基于30个单层厚壁圆筒的试验数据，采用似然分析理论与方法，对四个计算单层厚壁圆筒爆破压力的公式进行比较分析，为厚壁圆筒爆破压力的可靠性分析提供了基础数据.

2)对于K=1.33～4.71与γ=0.402 7～0.885 2的单层厚壁圆筒，在显著度为0.05时，其实测爆破压力与福贝尔公式(1)及式(2)～(4)的理论值之比，是基本符合正态分布的随机变量；在双侧置信度为98%时，得到该随机变量的均值、标准差与变异系数的取值区间.

3)如果公式(1)～(4)的应用范围为γ=0.402 7～0.885 2与K=1.33～4.71的单层厚壁圆筒，均值的精度依次由式(1)、(4)、(3)、(2)从高到低，变异系数的精度依次由式(2)、(3)、(1)、(4)从高到低.

4)如果适度改变公式的应用范围，对于γ=0.499 7～0.885 2与K=1.33～4.71的单层厚壁圆筒，公式(1)～(4)的精度会相应提高；在此应用范围内，均值的精度依次由式(1)、(4)、(3)、(2)从高到低，变异系数的精度依次由式(2)、(3)、(4)、(1)从高到低.

5)适度改变应用范围，可提高设计公式精度；在应用范围相同时，公式(1)～(4)的精度指标互有优劣，似存在精度比福贝尔公式高的公式.

致 谢

感谢湖北省教育厅科学技术研究项目组, 武汉市创新人才开发资金重大创新专项团队对本研究的支持与帮助.

[1] TSG R0002-2005超高压容器安全技术监察规程[S]. TSG R0002-2005 Super-high pressure vessel safety and technical supervision regulation[S].(in Chinese)

[2] 邵国华,魏龙灿.超高压容器[M].北京:化学工业出版社,2002:20-36. SHAO Guo-hua,WEI Long-can.Super-high pressure vessel [M].Beijing:Chemical Industry Publishing House,2002:20-36.(in Chinese)

[3] 柳爱群,杨中,杨烨.圆筒形压力容器爆破压力经验公式的改进[J].机械强度,2013,35(5):652-656. LIU Ai-quan,YANG Zhong,YANG Ye.Amendment of empirical formulas calculating bursting pressure of cylindrical vessels[J].Journal of Mechanical Strength,2013,35(5):652-656.(in Chinese)

[4] 徐灏.机械强度的可靠性设计[M].北京:机械工业出版社,1984. XU Hao.Mechanical strength reliability design[M].Beijing:Mechanical Industry Publishing House,1984.(in Chinese)

[5] 刘小宁,刘岑,张红卫,等.球形容器静强度的分布规律与参数[J].压力容器,2012,29(8):26-30. LIU Xiao-ning,LIU Cen,ZHANG Hong-wei,et al.Distribution law and parameters of spherical vessels static strength[J].Pressure Vessel Technology,2012,29(8):26-30.(in Chinese)

[6] 刘小宁,张红卫,刘岑,等.钢制薄壁内压容器静强度分布规律与参数分析[J].机械设计与研究,2012,28(5):66- 69. LIU Xiao-ning,ZHANG Hong-wei,LIU Cen,et al.Research on static strength distribution law and parameters of steel thin-walled internal pressure vessels[J].Machine Design and Research,2012,28(5):66-69.(in Chinese)

[7] 刘小宁,刘岑,张红卫,等.钢制薄壁长圆筒屈服强度分布规律与参数[J].机械设计,2013,30(1):45-48,54. LIU Xiao-ning,LIU Cen,ZHANG Hong-wei,et al.Distri- bution and parameters of steel thin-walled internal pressure long cylinder yield strength[J].Journal of Machine Design,2013,30(1):45-48,54.(in Chinese)

[8] 刘小宁,张红卫,刘岑,等.钢制内压容器可靠性安全系数的研究[J].武汉工程大学学报,2011,33(5):106-110. LIU Xiao-ning,ZHANG Hong-wei,LIU Cen,et al.Research on reliability safety factor of steel internal pressure vessel[J].Journal of Wuhan Institute of Technology,2011,33(5):106-110.(in Chinese)

[9] 刘兵，袁小会，刘岑，等.超高压容器用钢AISI4340的包辛格系数[J].武汉工程大学学报,2010,32(11):98-100. LIU Bing,YUAN Xiao-hui,LIU Cen,et al.Bauschinger coefficient of AISI4340 steel for Super-high pressure vessel[J].Journal of Wuhan Institute of Technology,2010,32(11):98-100.(in Chinese)

[10] 化学工程手册编辑委员会.化工应用数学[M].北京:化学工业出版社,1983:23-28,369-375. Editorial Board of Chemical Engineering Handbook.Mathematics of chemical application[M].Beijing:Chemical Industry Publishing House,1983:23-28,369-375.(in Chinese)

[11] 陈国理,钟汉通,王作池.超高压聚乙烯反应管爆破试验[J].压力容器,1991,8(2):40-43. CHEN Guo-li,ZHONG Han-tong,WANG Zuo-chi.Burst test of super-high pressure polyethylene reaction tube[J].Pressure Vessel Technology,1991,8(2):40-43.(in Chinese)

[12] 郑津洋,匡继勇,徐平,等.多层超高压容器爆破压力研究[J].化工机械,1994,21(5):271-277. ZHENG Ji-yang,KUANG Ji-yong,XU Ping,et al.Research intobursting pressures of the multi-layered super-high pressure vessel[J].Chemical Engineering & Machinery,1994,21(5):271-277.(in Chinese)

[13] 袁格侠,刘宏昭,钱学梅,等.求解超高压筒形容器爆破压力的神经网络方法[J].兵器材料科学与工程,2010,33(2):31-34. YUAN Ge-xia,LIU Hong-zhao,QIAN Xue-mei,et al.ANN-based prediction of bursting pressure under ultra-high pressure for cylindrical vessel[J].Ordnance Material Science and Engineering,2010,33(2):31-34.(in Chinese)

[14] 刘智敏.误差与数据处理[M].北京：原子能出版社, 1981. LIU Zhi-min.Errors and data processing[M].Beijing:Atomic Energy Publishing House,1981.(in Chinese)