基于二元离散选择模型的高校大学生考试挂科原因分析

丁咏梅，李寿贵，胡 杰，余 东

（武汉科技大学 理学院信息与计算科学系，湖北 武汉 430065）

基于二元离散选择模型的高校大学生考试挂科原因分析

丁咏梅，李寿贵，胡 杰，余 东

（武汉科技大学 理学院信息与计算科学系，湖北 武汉 430065）

基于Probit二元离散选择模型对影响大学生挂科的关键因素进行了实证分析，结果表明，学生学习时间对挂科与否有重大影响，而性别、健康状况和高考成绩对挂科与否影响并不显著。文章的最后，针对学生挂科现象，给出相应建议。

二元离散选择模型；效用模型；似然估计

进入大学，意味着未来有着高科技含量的工作、优厚的待遇、高尚的素养和品德。相较于中学，大学生活的确相对宽松，只要修满学位所需的课程和学分，就可以拿到相应的学位证和毕业证，自由度很大。同时各高校实现联合培养模式也为现代大学生提供了更多获取知识、信息的渠道，各种社团、学会给每位大学生提供一个展示自我、锻炼自身能力的平台。大学教育让每一位大学生尽可能做到人尽其学，各显其能。而评价某门课程是否学好的标准，主要的方式仍然是考试成绩。虽然象牙塔中的大多数学生都能明确学习目标、端正学习态度、不断完善自身，但是，近些年，挂科现象也不容忽视。一方面，挂科意味着学生对本门课程的基本知识掌握不足，另一方面，挂科也意味着教育成本、成长成本的增加。

一、挂科原因的定性分析

综合国内外关于大学生挂科原因，从定性的角度来分析，主要体现为以下几点：（1）学习目标不明确。大学的业余时间充足，常有丰富多彩的社团活动和各式各样的比赛。一部分同学把精力全部寄托于社团活动，本末倒置，不再学习。（2）自控能力差，沉迷网络。网络的诱惑是导致大学生挂科的重要原因。（3）盲目追求爱情。大学爱情美好而充满幻想。但是很多人急于在大学摆脱单身，是一种攀比性恋爱心理在作怪。（4）打工分散精力。有一部分同学打工的目的是为了减轻家庭负担，但是有些同学去打工，只是为了拥有更多的钱去吃喝玩乐。（5）课堂学习资源和信息欠缺。有研究表明，大量的由教师提供的网上课程资源与学生的低逃课率有关；另外，也有一些研究表明，讲课前运用多媒体放映一些跟教学内容相关的幻灯片可能对学生的出勤率和对课堂的参与性有积极影响。（6）学校对于师资的分配不合理。有的班级学生人数过多影响学生学习环境。有迹象表明，当课堂人数增加时，学生的平均成绩会出现下降。

二、挂科原因的定量分析

上面描述的大学生挂科原因涉及到的因素繁多，主次有待通过定量分析来确定，挂科以计数来定，即考查大学生的挂科门数。基于此，本文采取二元离散选择模型对大学生挂科的原因进行理论分析和实证研究。

1.二元离散选择模型。实际的社会生活中，我们常遇到二元选择问题。如公共交通和私人交通的选择问题，对某商品的购买决策问题，求职者对职业的选择问题等。本文以学生挂科问题为例，如果某个学生的效用为，上标表示“选择”结果，下标表示第i个个体。该效用是随机变量，并且由学生挂科状况所具有的属性和决策个体所具有的属性解释。于是有。类似地，如果某个个体“选择”不挂科，他的效用为，该效用是随机变量，并且由不挂科所具有的属性和决策个体所具有的属性解释。于是有。对于（1）和（2）模型中，效用是不可观测的，我们能得到的观测值仍是选择结果，即0和1。但是，如果不可观测的学生“选择”挂科的效用大于不挂科效用，对应的观测值为1；相反，如果不可观测的相应的观测值为0。将（1）与（2）相减：（3），记为：，我们可以对（4）进行计量分析和估计。对于学生“选择”Yi=1的概率显然应该有：

2.参数估计。模型（4）的被解释变量不可观测，显然不能采用最小二乘估计，只能采用最大似然估计。为了实现模型的最大似然估计，就必须为μi*选择一种特定的概率分布。两种最常用的分布是标准正态分布和逻辑分布，于是形成了两种最常用的二元选择模型——Probit模型和Logit模型。无论是标准正态分布还是逻辑分布，由于他们是对称的，存在F（-t）=1-F（t）（6）。式中F（t）表示概率分布函数。于是式（5）可以改写为P（Yi=1）=P（Yi*＞0）=P（μi*＞-Xiβ）=1-P（μi*≤-Xiβ）=1-F（-Xiβ）=F（Xiβ）（7）。至此，可以得到模型（4）的似然函数，，对数似然函数为lnL=，对数似然函数最大化的一阶条件为0（11）。式中fi表示概率密度函数。显然，在样本数据支持下，当（11）中的概率分布函数和概率密度函数已知时，求解该方程组，可以得到模型参数估计量。

3.实证分析。对于本文关于大学生考试挂科问题，据经验分析和文献研究的结果，影响大学生考试挂科的因素可能有高考成绩（CEE）、平时学习时间（平均每周用于学习的时间，Stime）、性别（Sex）、健康状况（Dbody）等。其中，性别和健康状况为虚拟变量：

我们把学生挂科（Unpass）定义为被解释变量，挂科为1，不挂科为0。选择武汉科技大学2012级的部分同学作为样本，选择问卷调查的方式，列出5个变量，由学生主动填写数据。发放问卷65份，回收65份，有效问卷62份，有效率为95%。为了进一步了解该样本特征，本文作者从学校教务系统中调出该样本的2013年秋季期末考试各门成绩，并统计出平时成绩，运用软件eviews7.0，得出其J-B统计量为3.04（如表3.1所示），相伴概率约为0.22，因此在90%的显著性水平下不能拒绝原假设，可以认为该样本来自正态总体。

表3 .1 数据的分布检验

高考成绩反映基础水平，平时学习时间反映努力程度，健康反映身体基础。基于以上数据收集，以不及格门数为被解释变量，建立二元离散模型。统计结果如表3.2。

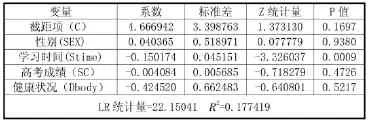
表3 .2 模型的参数估计结果

从表3.2中我们可以看出，性别和健康状况对挂科影响并不显著，高考成绩对其略有影响，而学习时间直接影响着考试挂科。从R2看，模型拟合效果并不好。为了更直观反映学习时间对挂科的影响，我们仍以考试挂科为因变量，以学习时间为自变量，建立模型，模型参数估计结果见表3.3。

表3 .3 估计结果

从以上结果中也可以看出，学习时间与考试挂科成负向关系，平时用的学习时间越少，挂科的可能性就越大，这也说明，欲减少挂科门数，必须在平时多投入时间，加强课后的学习和巩固。表3.3中我们可以得出相应的预测模型为Unpass=1-@CNORM（-（2.257056-0.143409*Stime））（12）。从估计结果可以发现，检验拟合优度的R2检验统计量的值为0.367694，检验总体显著性LR统计量的值为21.31330，表明模型具有较高的总体显著性；通过模型3.1可以得知，如果得到一个样本观测值，也就是知道某位学生的平时学习时间（Stime），代入方程中便可以得出相应的挂科（Unpass）概率，如观测值Stime=30时，代入方程右边，计算括号内的值为2.04，查看标准正态分布表，对应于2.04的累积正态分布为0.979，于是，该学生挂科（Unpass）的概率为0.021。

对二元离散选择模型的分析结果可以看出，高考分数对于挂科与否影响并不显著，一个主要原因是大部分同学入学时的高考成绩相当接近。性别和健康状况对挂科与否也没有重要影响。而学习时间对于学生挂科现象有显著影响。因此，充足的学习时间是至关重要的。其次，要树立正确的学习态度。大学是一个让自己从稚嫩变成熟的过程，要不断地从课堂、图书馆汲取知识的营养，丰富自己，以便造福于社会。同时作为教育管理者来说，建议丰富课堂教学手段，充实教学资源，且对班级人数进行合理规划安排，为学生和老师创造理想的学习、教学环境。

[1]辛桂京，高艺伦.大学生挂科探析J].高校讲坛，2012，（15）.

[2]李子奈，叶阿忠.高级应用计量经济学[M].北京：清华大学出版社，2012：122-125.

[3]C.Ryan Kinlaw，Linda L Dunlap，Jeffrey A.D’Angelo.Relations between faculty use of online academic resources and student class attendance[J].Computer&Education，2012，（59）：167-172.

G640

A

1674-9324（2014）35-0151-02

中国学位与研究生教育学会2013年研究课题（编号：C1-2013Y05-045）；湖北省自然科学基金重点项目（2013CFA131）。

丁咏梅（1978-），女，武汉科技大学理学院副教授，系统工程博士。