高职数学学习中思维定势的影响及教学策略

黄珽

张家港开放大学（张家港 215600）

高职数学学习中思维定势的影响及教学策略

黄珽

张家港开放大学（张家港 215600）

对待数学教学中的思维定势，我们应采取一分为二的态度，慎重处理。本文主要探讨了如何发挥思维定势在数学学习中的积极作用，消除思维定势的消极影响，培养学生数学思维能力。

高职数学 思维定势 数学教学

人类在处理问题时，一般会根据累积的经验解决，并在多次反复使用和成功后，形成比较稳定的、定型化的思维方式，并影响着后续知识学习和问题的解决方式，这种思维的习惯性倾向我们称之为思维定势。

1 思维定势对高职数学学习的影响

1.1 思维定势的正迁移

高职学生在数学学习的过程中，依据已学的数学理论和方法：概念、定理、公式等，对新的知识分解、消化，并利用已有的经验和知识进行系统化的整理，最终掌握新知，从而实现了思维定势的正迁移。

1.2 思维定势的负迁移

关于思维定势的负迁移有一个著名的心理实验：35名大学生被要求用6根等长火柴搭出4个三角形（三角形的每条边长为一根火柴长）。结果只有10人在无任何提示下成功完成，18人在暗示下也成功了，但最后仍有7人没有成功。而造成解题障碍的主要原因是他们将问题的解决局限在了一个平面内，而一旦有人将之打破，问题便迎刃而解。思维定势的负迁移造成人们思考问题角度单一，形成思维惰性，限制了创造性思维能力。在数学教学中，思维定势的消极作用主要有以下几点：

（1）概念、定理、公式、法则定势的负迁移

学生在学习新的知识和解决数学问题时，首先会联系现有的数学概念、定理、公式和法则等。因为，原先掌握的知识、方法已经深深地刻在了学生头脑中。在思维定势的作用下，学生总是在惯性思维的作用下思考问题，在潜意识中不知不觉地排斥新的概念和方法。

例1在棱长为a正方体中，求对角线AC1的长度。班级共有39名学生，其中27名学生利用平面几何的知识解答，10名学生利用了刚刚学习的向量知识，还有2名学生不会做。其中利用几何平面解题正确的率为74%，而利用向量求解的正确率为100%，计算速度也快得多。相比较而言，运用向量的方法明显要方便简单的多。

图1 求AC1长

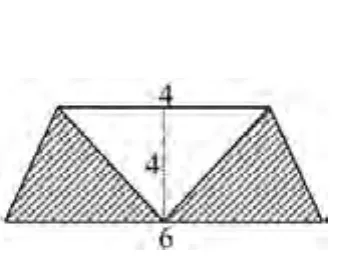
图2 求阴影面积（a）

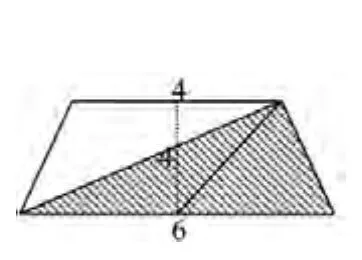
图3 求阴影面积（b）

（2）思维方法定势的负迁移

高职学生在解决数学问题时，容易形成一种固定的解题模式，不能随机应变，导致解题遇难，简单问题复杂化，造成数学学习上的负迁移。

例3猴子摘了一堆桃子，第一天吃了桃子一半多一个，以后每天都吃尚存桃子的一半加一个，到了第10天还剩一个，请问猴子一共摘了多少桃子？

班级中的大部分同学采用了假设的方法解题，假设猴子一共摘了n个桃子

第二天还剩：n-（n/2+1）=n/2-1

第三天还剩：n/2-1-（（n/2-1）/2+1）

大部分学生在解答到第三天或第四天的时候不愿意再尝试下去了，坚持到最后的也没有计算出正确答案，学生都抱怨太复杂，计算量太大。其实，这道题只要反过来一想，就没有那么复杂：

第10天剩余桃数：1

第9天剩余桃数：（1+1）×2=4

第8天剩余桃数：（4+1）×2=10

……

规律很明显，即每天剩余的桃数是后一天桃数加1的两倍。如果我们从第九天开始计算很容易就能得到答案。

（3）学习品质定势的负迁移

高职学生的数学基础相对薄弱，没有形成良好的学习习惯，在以往数学的学习中，饱受挫折，他们大多在学习上缺乏明确的学习目标，在解题的过程中更多的依附于标准答案和他人，缺乏独立思考的能力，养成了浅尝则止，遇难即退，人云亦云的学习品质，即使对问题有自己的见解也不敢表达，缺乏自信和主动性，这些不良的学习品质加重了数学思维定势的负迁移。

2 高职数学教学策略

2.1 充分发挥思维定势正效应，提高学生解题能力

2.1.1 夯实基础，融会贯通

数学知识的学习是一个渐进的过程，巩固所学知识，保证概念清晰是学好数学的关键。许多高职学生在概念、定理、公式学习时，没有深入分析公式定理的应用条件，概念所包含的前提条件，流于表面。在解决问题时，生搬硬套，一旦实际问题稍有变化便束手无策。教师应把握高职学生数学学习的特点，应用多元化的教学手段，将数学概念讲解透彻，并配以适当的练习，帮助学生巩固。

2.1.2 以旧引新，循序渐进

教师在数学教学中要注意引导学生复习旧知，在深入挖掘已有知识的内涵和规律的基础上探索新知的规律，从而促进知识的正迁移。例如在介绍n凸多边形的内角和定理时，可以按以下4步走：（1）复习三角形的内角和定理；（2）在学生熟练掌握三角形的内角和定理的前提下，提示学生如何计算四边形的内角和（分割为2个三角形）；（3）在学生掌握分割三角形方法的基础上，让学生独立计算五边形、六边形；（4）根据计算得到的规律，学生总结n凸多边形的内角和。在利用旧知（三角形内角和定理）的正效应后，新的知识就很容易被学生接受。

2.2 消除固定思维负效应，培养学生发散性思维能力

2.2.1 精心设计，项目引领

数学究其本质就是探究问题的方法，数学活动是包含猜测、假设、尝试、证明、反驳、检验、改进与归纳的复杂过程。教师在课程设计时，需要将数学教学与学生专业相结合，以实用数学能力培养需要带动数学知识的学习。在项目教学案例的引领下，数学知识点的教学设计应根据学生的认知规律，在情境教学中巧妙引入，通过巧设问题、思考尝试、分组讨论、解决问题和归纳总结五个步骤循序渐进的引领学生在实际问题的解决过程中完成新知识的学习。项目化的教学方式遵循学生的认知规律，贴近工作、生活实际，有利于激发学生的学习兴趣，让学生主动参与讨论，并在反复尝试中最终获得知识，增强学生对知识点的理解和记忆。实践证明，在解决实际问题的过程中获取的知识更有利于学生的掌握和吸收，可以有效地消除思维定势的负迁移。

2.2.2 变式训练，灵活运用

数学的学习过程不能仅仅依靠教师，要让学生有效地掌握数学知识，还需要培养学生的发散性思维能力。教师可以在一个问题上，设置不同的条件或者在原问题解决的基础上提出引申问题，拓展学生思路，培养学生数学发散性思维能力，摆脱满足窄向思维的消极影响。

如求图2阴影部分的面积：S=S梯形—S三角形。如图给定了梯形的上底、下底和高，当然很容易求得。

这时提出新问题：如果上底的长度未知，求阴影部分的面积。此时，教师可以采用小组讨论、组间交流的方式进行，教师扮演引导者的角色，让学生自己找到答案。最后，教师可通过动画演示将阴影面积图形改变为图3，直接求得阴影面积。

通过改变条件不断地引导学生思考，有利于培养学生的发散性思维能力，从而避免思维定势带来的干扰。

2.2.3 一题多解，寻求最优

一个数学问题的解决往往不止一种方法，教师要注意培养学生的创造性思维能力，引导学生对问题认真思考，从不同的角度探索不同的解法，注意培养学生敢于想、敢于试的学习态度，打破固定思维的桎梏，在教学中引导学生多尝试，并及时的鼓励，克服学生数学学习中的自卑感。

总之，教师在高职数学的教学中，一定要注意引导学生养成独立思考、善于分析的学习习惯，只有这样才可以不断克服思维定势的消极影响，发挥思维定势的积极作用，在数学教育中打开一个全新的局面。

[1]吴叶民.思维定势在高等数学教学中的影响及教学策略[J].中小企业管理与科技,2011,（12）:293-294.

[2]王钊,肖宏治.浅谈数学教学中思维定势与思维发散[J].长春理工大学学报,2012,（6）:208-209.

文婷）