圆柱斜齿轮鼓形齿修形量计算验证与齿形三维建模
2014-02-24关欣
关 欣
辽宁广播电视大学 (沈阳 110034)
从斜齿轮的失效形式来看,疲劳点蚀是闭式齿轮传动中的主要失效形式之一。引起失效的直接原因是接触应力的不断变化,而对接触应力大小影响的原因是由于齿廓变形、加工误差、安装误差以及布置形式等。实践研究表明,对齿轮齿向进行适当的修形,可以大大缓解因齿向应力不均带来的齿轮失效[1]。齿向修形主要是对齿轮沿齿向方向进行微量的修整齿面,使其偏离理论齿面。通过齿向修形可以改善载荷沿轮齿接触线的不均匀分布的现象,可以大大提高齿轮承载能力。齿向修形的方法有齿端修薄、螺旋角修形、鼓形齿等[2,3]。
1 鼓形齿修形鼓形量的计算
鼓形齿轮齿在齿宽中央鼓起,两边呈对称状。鼓形齿设计方法简单,修形效果明显,加工方便,而且容易控制质量和发现问题,应用广泛。
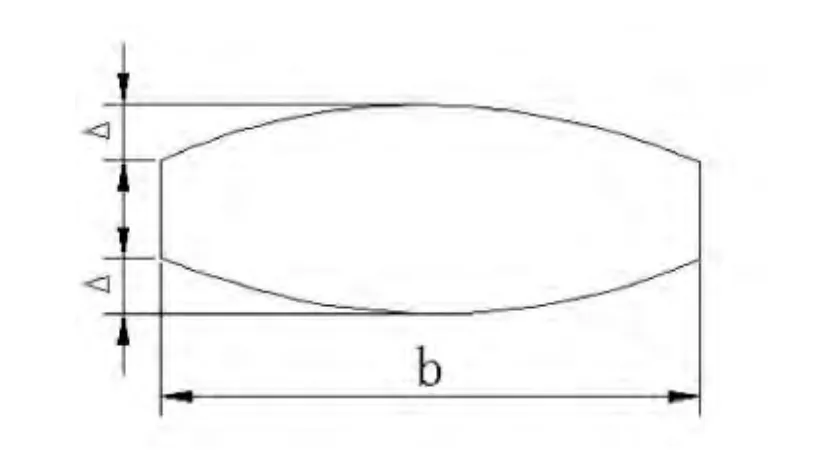
图1 鼓形齿图
鼓形齿最主要的目的是保证齿轮在最大啮合歪斜度的条件下相互啮合的轮齿不发生端点接触(即相切而不相交)。同时在齿轮轴线相对于理论轴线稍微倾斜的情况下,最大限度地减少单位齿宽上的载荷。此外,轮齿是一个弹性体,受载后发生变形,从而影响轮齿的接触情况。
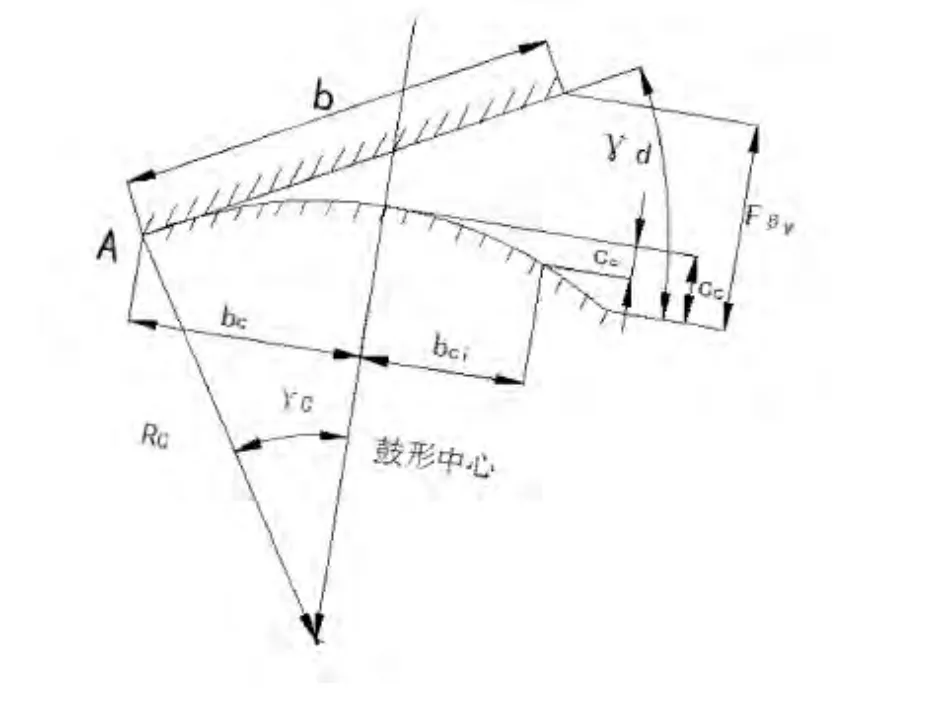
图2 鼓形中心的确定
考虑啮合歪度与弹性变形,按照斜齿轮啮合线长度与齿宽的关系,鼓形量计算式为[4]:

其中:
Cγ——齿轮综合刚度;
Fβy——齿轮啮合歪斜度;
Fr——径向力;
B——齿宽
公式(1)用于实际啮合线大于齿宽时的问题,公式(2)用于实际啮合线小于齿宽的问题。
一般来说,鼓形齿的鼓形的中心应选在齿宽的中部。由图2可知,确定鼓形中心为已知圆上两点和半径,求圆心的问题。
鼓形圆弧的半径为:

其中bc为半齿宽,Cc为鼓形量。
啮合歪度Fβy决定齿形在齿宽方向实际位置相对理论位置的偏离程度。影响啮合歪度的因素主要包括空间几何误差、构件刚度以及工作条件。文献[2]中给出了考虑到以上因素的歪度表达式,但目前歪度计算仍没有公认的方法。本文采用文献[2]中给出的考虑装配误差以及轴的弯扭变形情况下的歪度计算式:

其中:
fsh——轴的弯扭变形产生的啮合歪度
fp——装配误差产生的啮合歪度
Yβ——跑合量,取0.15Fβy
公式(4)中的fp与安装的轴承跨距有关,如图3所示。
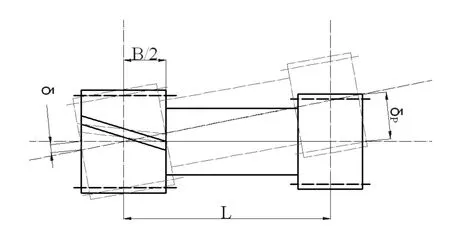
图3 轴承跨距
按照其轴承跨距,可以查得啮合齿轮轴线之间的平行度公差。平行度公差δp向实际平行度偏差转化为:

啮合刚度的确定根据文献[3]中的研究结果,一对外啮合的斜齿轮其啮合刚度可以近似取 Cγ=22 N/(μm·mm)。
由以上计算结果,可以得到鼓形修形量的计算公式:

公式(6)仅需要按照齿轮加工以及装配的公差等级查得偏差值,并按照齿轮的工作参数便可计算鼓形齿的修形量。
2 鼓形齿的PROE实现
按鼓形齿形状,在PRO/E中可以对未修形的齿轮进行修改,以建立鼓形齿轮。采用扫面混合法,将齿轮的扫面混合的端面进行修整,如图4所示,为了便于观察,将鼓形量放大了80倍。

图4 对扫面混合剖面修整
将扫描混合所需的N个截面(N>3)进行不同程度的修整(如图4所示),再重新完成扫描混合特征,便可得到鼓形齿(如图5所示)。
在扫描混的过程中应特别注意各端面混合节点的设定,必须保证混合所涉及到的各节点的相互对应关系,否则生成的轮齿会发生扭曲。

图5 鼓形齿
3 算例与有限元验证
以一对大小形同的斜齿轮为计算模型,其模数m=3.5,齿数nt1,nt2=32,螺旋角β=16°,齿宽B=20 mm,材料的弹性模量E=2e11 Pa,泊松比μ=0.3,许用接触应力1250 Mpa,轴承跨距L=100 mm,摩擦系数为0.06,加载力矩M=500 N·m,其余参数均为标准值,取所有公差等级8级。
按照8级精度,查得齿轮啮合歪度计算所需参数值为:

由公式(6)算得鼓形修形量,并圆整:

按照计算模型中的装配误差,在PROE中建立存在误差的齿轮啮合模型,将其导入Workbench中进行计算,接触应力分布及最大应力值如图6所示。

图6 考虑装配偏差时的结果
在考虑装配误差时,齿轮进入啮合的端面处存在着应力集中,该应力值为2602.9 MPa,已经超过了齿轮材料的许用接触应力,会造成齿面的压溃。
将计算得到的修形量与鼓形齿建模方法实装于斜齿轮的参数化模型,建立修形后的齿轮啮合模型。将模型导入Workbench求解计算。计算结果如图7所示。

图7 修形后的接触应力
从图7可以看出,修形后过轮对的接触应力有所下降,为1003.3 MPa,且不存在齿轮端部的应力集中状况(修形量相对于齿轮尺寸很小,在计算结果上无法观察到齿端应力,实际上,鼓形齿在端部不发生啮合,故在齿端处不存在接触应力)。可见,根据公式(6)算得的修形量对装配误差造成的应力集中有明显的改善效果。
4 结语
从齿轮修形的基本理论与方法出发,探讨了鼓形齿的原理及修形方式,对鼓形齿修形在PROE中实现提供了方法。对鼓形修形后的计算模型进行了两种状态下的应力分析:考虑平行度误差未修形状态以及考虑平行度误差修形后的状态。通过对两种状态下接触应力值与最大接触应力位置的对比,验证了修形公式的合理性。
[1]方宗德,张永才.斜齿轮的齿廓修形[J].汽车工程,1993,15(1):59-64.
[2]方宗德.修形斜齿轮的轮齿接触分析[J].航空动力学报,1997,12(3):247-250.
[3]张展.齿廓修形与齿向修形[J].建筑机械,1987,(10):34-39.
[4]宋乐民.齿形与齿轮强度[M].北京:国防工业出版社,1987.
